Compaction within a Model with Nonuniform Zoning

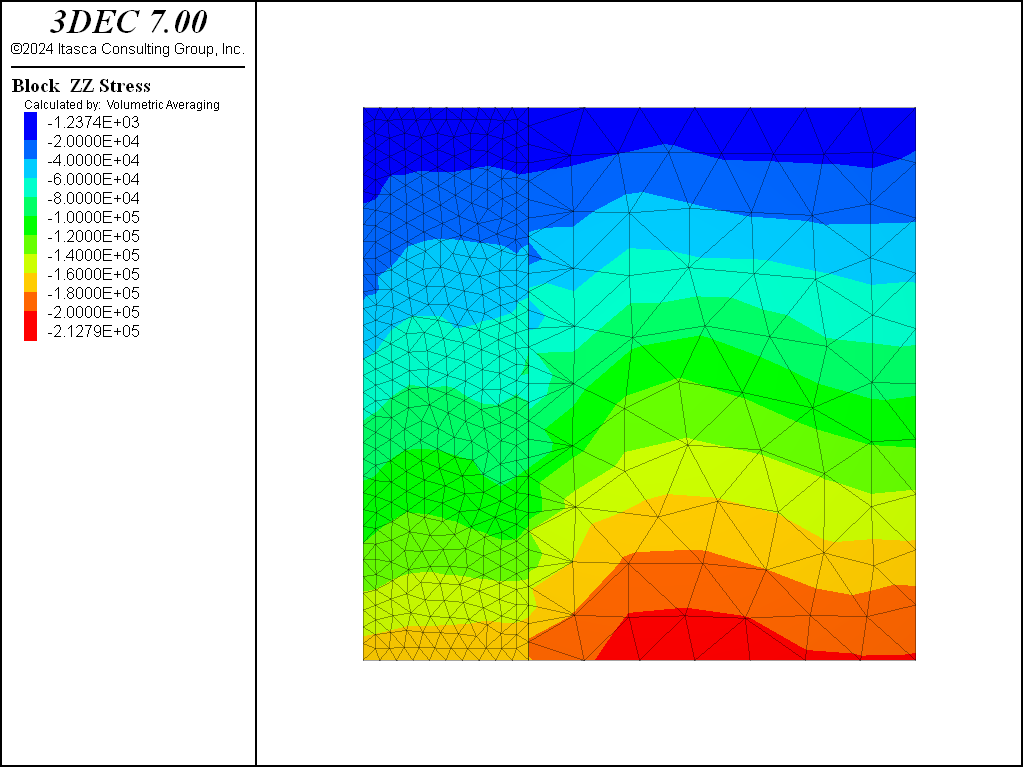
Puzzling results are sometimes observed when a model with nonuniform zoning is allowed to come to equilibrium under gravity. A model that is composed of deformable blocks of different sizes will usually have nonuniform zoning. When a Mohr-Coulomb (or other nonlinear constitutive) model is assigned to the blocks, the final stress state and displacement pattern are not uniform, even though the boundaries are straight and the free surface is flat. The data file in the example below illustrates the effect (see the figure following for the generated plot showing vertical stress contours):

Nonuniform stress initialized in a model with nonuniform zoning

model new
model random 10000
model large-strain off

block create brick 0,10 0,2  0,10
;
block cut joint-set dip 90.0 dip-direction 90 origin 3,0,0 join
block hide range pos-x 3 10
block zone generate edgelength 0.3
block hide off
block zone generate edgelength 1.0
;
block zone cmodel assign mohr-coulomb
block zone prop  dens 2000 bulk 2e8 shear 1e8 friction 30
;
model gravity 0 0 -10

block gridpoint apply vel-x = 0.0 range pos-x  0.0
block gridpoint apply vel-x = 0.0 range pos-x 10.0
block gridpoint apply vel-y = 0.0 range pos-y  0.0
block gridpoint apply vel-y = 0.0 range pos-y 2.0
block gridpoint apply vel-z = 0.0 range pos-z  0.0
;
model history mechanical unbalanced-maximum
model save 'initial'
model solve
model save 'initial-1'

Figure 1: Nonuniform stresses

Since we have roller boundaries on the four sides, we might expect the material to move down equally on all sides. However, the zones are not the same size in the blocks. For static analysis, 3DEC tries to keep the timestep equal for all zones, so it increases the inertial mass for the gridpoints of the smaller zones to compensate for their size. These gridpoints then accelerate more slowly than those for the larger zones. This would have no effect on the final state of a linear material, but it causes nonuniformity in a material that is path-dependent. For a Mohr-Coulomb material without cohesion, the situation is similar to dropping sand from some height into a container and expecting the final state to be uniform. In reality, a large amount of plastic flow would occur because the confining stress does not build up immediately. Even with a uniformly zoned model, this approach is not a good one because the horizontal stresses depend on the dynamics of the process.

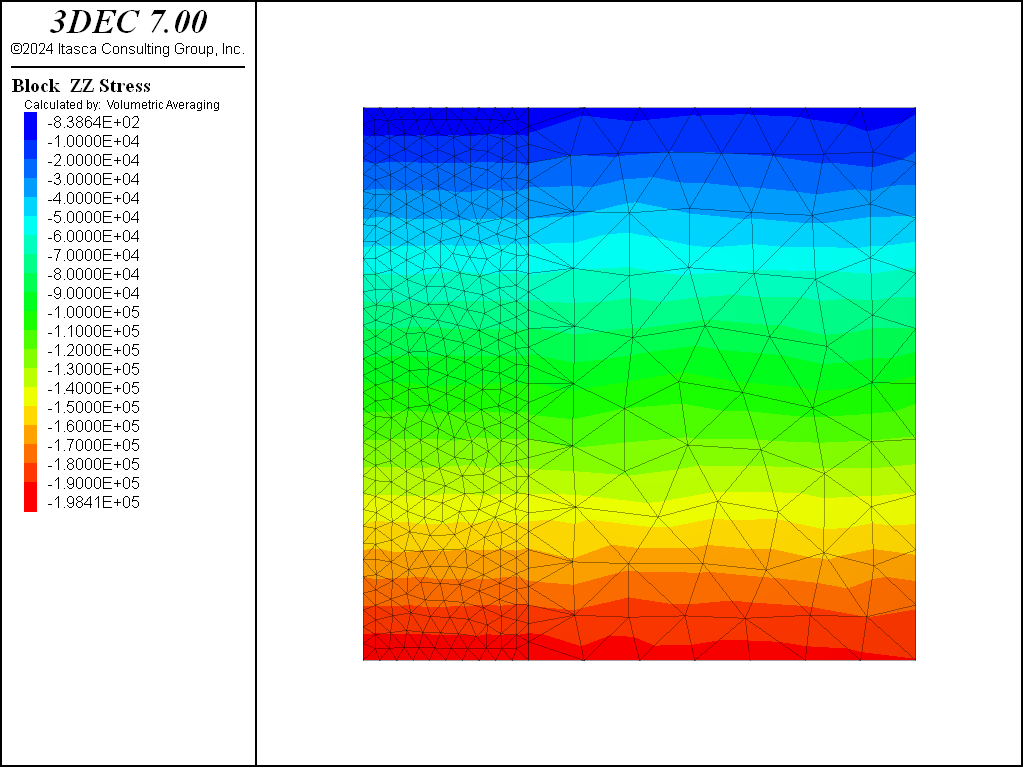
The best solution is to use the block insitu command to set initial stresses to conform to the desired \(K_o\) value (ratio of horizontal to vertical stress). For example, the model solve command in the previous data file could be replaced by the following lines:

block insitu topography ratio-x 0.75 ratio-y 0.75
model solve

A stable state is achieved with \(K_o\) = 0.75; fewer steps are needed to reach equilibrium, and the stress state is uniform (see the figure below). Note that there is a slight nonuniformity, but this is related to the contouring routine and the coarseness of the zoning.

Alternatively, the model can be run with an elastic behavior for the initial equilibrium calculation, and then changed to the nonlinear behavior model for the final state. Replace the model solve command with the following lines:

model solve elastic

The result is the same as that shown in the figure below. The material is prevented from yielding during the compaction process, but the original properties are restored when equilibrium is achieved.

Figure 2: Uniform stresses