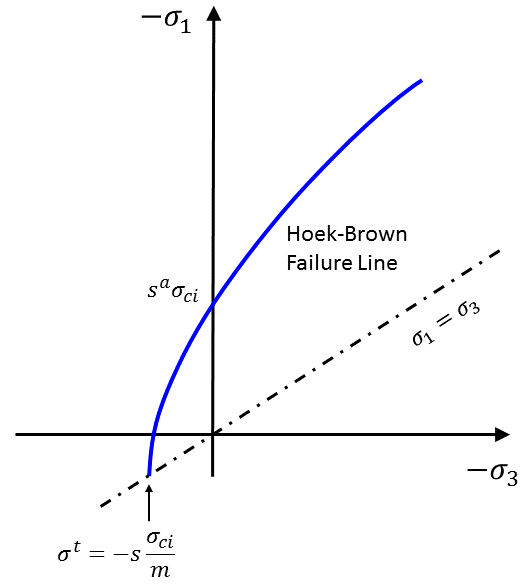Hoek-Brown-PAC Model
The Hoek-Brown failure criterion is an empirical relation that characterizes the stress conditions that lead to failure in intact rock and rock masses. It has been used very successfully in design approaches that use limit equilibrium solutions, but there has been little direct use in numerical solution schemes. Alternatively, equivalent friction and cohesion have been used with a Mohr-Coulomb model that is matched to the nonlinear Hoek-Brown strength envelope at particular stress levels Numerical solution methods require full constitutive models, which relate stress to strain in a general way; in addition to a failure (or yield) criterion, a “flow rule” is also necessary, in order to provide a relation between the components of strain rate at failure. There have been several attempts to develop a full constitutive model from the Hoek-Brown criterion: Pan and Hudson (1988), Carter et al. (1993) and Shah (1992), for example. These formulations assume that the flow rule has some fixed relation to the failure criterion, and that the flow rule is isotropic, whereas the Hoek-Brown criterion is not. In the formulation described here, there is no fixed form for the flow rule: it is assumed to depend on the stress level, and possibly some measure of damage.
In what follows, the failure criterion is taken as a yield surface, using the terminology of plasticity theory. Usually, a failure criterion is assumed to be a fixed, limiting stress condition that corresponds to ultimate failure of the material. However, numerical simulations of elastoplastic problems allow continuing the solution after “failure” has taken place, and the failure condition itself may change as the simulation progresses (by either hardening or softening). In this event, it is more reasonable to speak of “yielding” than failure. There is no implied restriction on the type of behavior that is modeled: both ductile and brittle behavior may be represented, depending on the softening relation used.
General Formulation
The “generalized” Hoek-Brown criterion (Hoek and Brown, 1980 and 1998), adopting the convention of positive compressive stress, is
where \(\sigma_1\) and \(\sigma_3\) are the major and minor effective principal stresses, and \(\sigma_{ci}\), \(m_b\), \(s\), and \(a\) are material constants that can be related to the Geological Strength Index (\(GSI\)) and rock damage (Hoek et al. 2002). For interest, the unconfined compressive strength is given by \(\sigma_{c}\) = \(\sigma_{ci}\) \(s^a\), and the tensile strength by \(\sigma_{t}\) = - \(s\) \(\sigma_{ci}\) / \(m_b\), (see Figure 1). Note that the criterion (Equation (1)) does not depend on the intermediate principal stress, \(\sigma_{2}\). Thus, the failure envelope is not isotropic.
Assume that the current principal stresses are (\(\sigma_1,\sigma_2,\sigma_3\)), and that initial trial stresses (\(\sigma_1^t\), \(\sigma_2^t\), \(\sigma_3^t\)) are calculated by using incremental elasticity:
where \(E_1 = K + 4G/3\) and \(E_2 = K - 2G/3\), and (\(\Delta e_1,\Delta e_2,\Delta e_3\)) is the set of principal strain increments. If the yield criterion (Equation (1)) is violated by this set of stresses, the strain increments (prescribed as independent inputs to the model) are assumed to be composed of elastic and plastic parts:
Note that plastic flow does not occur in the intermediate principal stress direction. The final stresses (\(\sigma_1^f\), \(\sigma_2^f\), \(\sigma_3^f\)) output from the model are related to the elastic components of the strain increments. Hence:
Eliminating the current stresses, using Equations (2) and (4):
We assume the flow rule
where the factor \(\gamma\) depends on stress and is recomputed at each timestep. Eliminating \(\Delta e_1^p\) from Equation (5):
At yield, Equation (1) is satisfied by the final stresses. That is,
By substituting values of \(\sigma_1^f\) and \(\sigma_3^f\) from Equation (7), Equation (8) can be solved iteratively for \(\Delta e_3^p\), which is then substituted in Equation (7) to give the final stresses. The method of solution is described later, but first the evaluation of \(\gamma\) is discussed.
Flow Rules
We need to consider an appropriate flow rule, which describes the volumetric behavior of the material during yield. In general, the flow parameter \(\gamma\) will depend on stress, and possibly on history. It is not meaningful to speak of a “dilation angle” for a material when its confining stress is low or tensile, because the mode of failure is typically by axial splitting, not shearing. Although the volumetric strain depends, in a complicated way, on stress level, we consider certain specific cases for which behavior is well-known, and determine the behavior for intermediate conditions by interpolation. Three cases are considered:
Associated Flow Rule
It is known that many rocks under unconfined compression exhibit large rates of volumetric expansion at yield, associated with axial splitting and wedging effects. The associated flow rule provides the largest volumetric strain rate that may be justified theoretically. This flow rule is expected to apply in the vicinity of the uniaxial stress condition (\(\sigma_3 \approx 0\)). An associated flow rule is one in which the vector of plastic strain rate is normal to the yield surface (when both are plotted on similar axes). Thus,
where the subscripts denote the components in the principal stress directions, and \(F\) is defined by Equation (8). Differentiating this expression, and using Equation (6),
Radial Flow Rule
Under the condition of uniaxial tension, we might expect that the material would yield in the direction of the tensile traction. If the tension is isotropically applied, we imagine (since the test is almost impossible to perform) that the material would deform isotropically. Both of these conditions are fulfilled by the radial flow rule, which is assumed to apply when all principal stresses are tensile. For a flow-rate vector to be coaxial with the principal stress vector, we obtain
Constant-Volume Flow Rule
As the confining stress is increased, a point at which the material no longer dilates during yield is reached. A constant-volume flow rule is therefore appropriate when the confining stress is above some user-prescribed level, \(\sigma_3 = \sigma_3^{\rm cv}\). This flow rule is given by
Composite Flow Rule
We propose to assign the flow rule (and, thus, a value for \(\gamma\)) according to the stress condition. In the fully tensile region, the radial flow rule (\(\gamma_{\rm rf}\)) will be used. For compressive \(\sigma_1\) and tensile or zero \(\sigma_3\), the associated flow rule (\(\gamma_{\rm af}\)) is applied. For the interval \(0 < \sigma_3 < \sigma_3^{\rm cv}\), the value of \(\gamma\) is linearly interpolated between the associated and constant-volume limits:
Finally, when \(\sigma_3 > \sigma_3^{\rm cv}\), the constant-volume value, \(\gamma = \gamma_{\rm cv}\), is used.
If \(\sigma_3^{\rm cv}\) is set equal to zero, then the model condition approaches a nonassociated flow rule with a zero dilation angle. If \(\sigma_3^{\rm cv}\) is set to a very high value relative to \(\sigma_{ci}\), the model condition approaches an associated flow state.
Implementation Procedure
The equations presented above are implemented. One difficulty with the failure criterion Equation (8) is that real values for \(F\) do not exist if \(\sigma_3 < -s \sigma_{ci} / m_b\). During an iteration process, this condition is likely to be encountered, so it is necessary that the expression for \(F\), and its first derivatives, be continuous everywhere in stress space. This is fulfilled by adapting the composite expression
To initialize the iteration, a starting value for \(\Delta e_3^p\) is taken as the absolute maximum of all the strain increment components. This value, denoted by \(\Delta e_1\), is inserted into Equation (7), together with the value for \(\gamma\) found from the flow-rule equations, and the resulting stress values inserted into Equations (14) and (15). The resulting value of \(F\) is denoted by \(F_1\). Taking the original value of \(F\) as \(F_0\) (and the corresponding plastic strain increment of zero as \(\Delta e_0\)), we can estimate a new value of the plastic strain increment, using a variant of Newton’s method:
From this, we find a new value of \(F\) (call it \(F_2\)) and, if it is sufficiently close to zero, the iteration stops. Otherwise, we set \(F_0 = F_1\), \(F_1 = F_2\), \(\Delta e_0 = \Delta e_1\), and \(\Delta e_1 = \Delta e_2\) and apply Equation (16) again.
Tests show that the iteration scheme converges for all stress paths tried so far, including cases in which \(s\) = 0 (material with zero unconfined compressive strength), which led to problems in previous implementations. For high confining stresses, the iteration converges in one step, but at low confining stresses, up to ten steps are necessary (the limit built into the code is presently 15).
Material Softening
In the Hoek-Brown model, the material properties \(\sigma_{ci}\), \(m_b\), \(s\), and \(a\) are assumed to remain constant, by default. Material softening after the onset of plastic yield can be simulated by specifying that these mechanical properties change (i.e., reduce the overall material strength) according to a softening parameter. The softening parameter selected for the Hoek-Brown model is the plastic confining strain component, \(e^p_3\). The choice of \(e^p_3\) is based on physical grounds. For yield near the unconfined state, the damage in brittle rock is mainly by splitting (not by shearing) with crack normals oriented in the \(\sigma_3\) direction. The parameter \(e^p_3\) is expected to correlate with the microcrack damage in the \(\sigma_3\) direction.
The value of \(e^p_3\) is calculated by summing the strain increment values for \(\Delta e^p_3\) calculated by Equation (16). Softening behavior is provided by specifying tables that relate each of the properties \(\sigma_{ci}\), \(m_b\), \(s\), and \(a\) to \(e^p_3\). Each table contains pairs of values: one for the \(e^p_3\) value, and one for the corresponding property value. It is assumed that the property varies linearly between two consecutive parameter entries in the table.
A multiplier, \(\mu\) (denoted as multable), can also be specified to relate the softening behavior to the confining stress \(\sigma_3\). The relation between \(\mu\) and \(\sigma_3\) is also given in the form of a table. (See Cundall et al. (2003) for an application of softening parameters.)
References
Carter, T. G., J. L. Carvalho and G. Swan. “Towards the Practical Application of Ground Reaction Curves,” in Innovative Mine Design for the 21st Century (Proceedings of the International Congress on Mine Design — Kingston, Ontario, Canada — August 1993), pp. 151-171. W. F. Bawden and J. F. Archibald, eds. Rotterdam: A. A. Balkema (1993).
Cundall, P., C. Carranza-Torres and R. Hart. “A New Constitutive Model Based on the Hoek-Brown Criterion,” in FLAC and Numerical Modeling in Geomechanics — 2003 (Proceedings of the 3rd International FLAC Symposium, Sudbury, Ontario, Canada, October 2003), pp. 17-25. R. Brummer et al., eds. Lisse: Balkema (2003).
Hoek, E., C. Carranza-Torres and B. Corkum. “Hoek-Brown Failure Criterion — 2002 Edition,” in Proceedings of NARMS-TAC 2002, 5th North American Rock Mechanics Symposium and 17th Tunnelling Association of Canada Conference — Toronto, Canada — July 7 to 10, 2002. Vol.~1., pp. 267-271. R. Hammah et al., eds. Toronto: University of Toronto Press (2002).
Pan, X. D., and J. A. Hudson. “A Simplified Three Dimensional Hoek-Brown Yield Criterion,” in Rock Mechanics and Power Plants (Proceedings of the ISRM Symp.), pp. 95-103. M. Romana, ed. Rotterdam: A. A. Balkema (1988).
Shah, S. A Study of the Behaviour of Jointed Rock Masses. Ph.D. Thesis, University of Toronto (1992).
hoek-brown-pac Model Properties
Use the following keywords with the zone property (FLAC3D) or block zone property (3DEC) command to set these properties of the Hoek-Brown-PAC model.
- hoek-brown-pac
- bulk f
bulk modulus, \(K\)
- constant-a f
Hoek-Brown parameter, \(a\)
- constant-mb f
Hoek-Brown parameter, \(m_b\)
- constant-s f
Hoek-Brown parameter, \(s\)
- constant-sci f
Hoek-Brown parameter, \(\sigma_{ci}\)
- poisson f
Poisson’s ratio, \(\nu\)
- shear f
shear modulus, \(G\)
- stress-confining-prescribed f
Hoek-Brown parameter, confining stress at user-prescribed level, \(\sigma^{cv}_3\)
- young f
Young’s modulus, \(E\)
- strain-3-plastic f (a)
accumulated plastic strain in direction of least compressive principal stress, \(e^p_3\)
- table-a s (a)
name of the table relating \(a\) to \(e^p_3\).
- table-mb s (a)
name of the table relating to \(m_b\) to \(e^p_3\).
- table-multiplier s (a)
name of the table relating a multiplier to \(\sigma_3\).
- table-s s (a)
name of the table relating \(s\) to \(e^p_3\).
- table-sci s (a)
name of the table relating \(\sigma_{ci}\) to \(e^p_3\).
- number-iteration i (r)
number of iterations
Key
- (a) Advanced property.
- This property has a default value; simpler applications of the model do not need to provide a value for it.
- (r) Read-only property.
- This property cannot be set by the user. Instead, it can be listed, plotted, or accessed through FISH.
Notes
- Only one of the two options is required to define the elasticity: bulk modulus \(K\) and shear modulus \(G\), or Young’s modulus \(E\) and Poisson’s ratio \(\nu\). When choosing the latter, Young’s modulus \(E\) must be assigned in advance of Poisson’s ratio \(\nu\).
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |