General Formulation of Structural-Element Logic
The low-level implementation details of the structural-element logic are presented here. This information need only be read by users interested in gaining a thorough understanding of the implementation (perhaps, in order to implement nonstandard interaction between structural elements and the grid). The structural-element logic has been developed in a general and flexible fashion in order to support various (as yet unforeseen) application scenarios.
Structural-Element Links
Structural elements only interact with one another via nodes; and nodes, in turn, only interact with the grid via links. Thus, structural-element links provide the sole means by which structural elements interact with the grid. Each link connects a node to a target entity. Each node may only have one link associated with itself. There are two types of links: (1) node-to-zone, which connect nodes to zones (not simply to gridpoints); and (2) node-to-node, which connect nodes to other nodes.
In addition to localizing the interaction between structural elements and the grid, links also provide a general mechanism for implementing nonlinear constitutive behavior at a node, in terms of that node’s local coordinate system. A link supports the following three attachment conditions, which are specified independently for each local direction of its source node:
- free Velocity of the source node in this local direction is unrelated to the velocity of the target entity.
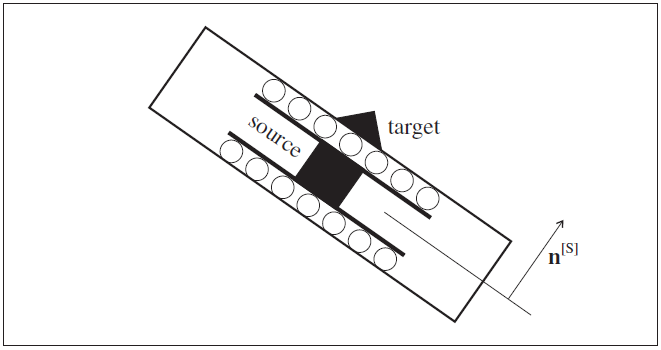
- rigid Velocity of the source node in this local direction is slaved to remain equal to the component of the velocity of the target entity in this direction (see Figure 1).
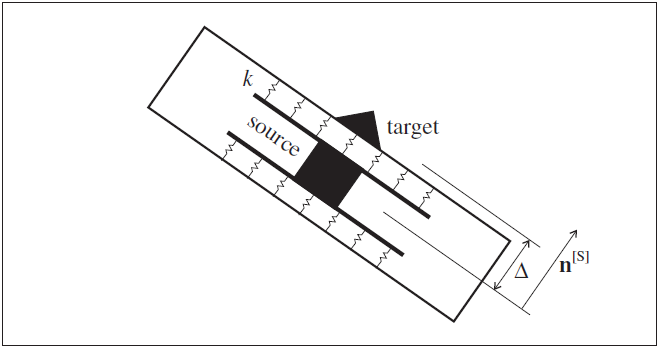
- deformable Denote the attachment direction by \({\bf n}^{[{\rm S}]}\). The source node and target entity are connected by a spring oriented in the direction \({\bf n}^{[{\rm S}]}\). The spring stiffness is an average stiffness per unit area associated with the link (see Figure 2).
Deformable attachment conditions allow generalized constitutive models, which relate increments of displacement and total force in a particular local direction, to be included in the model. There are a total of five such models used to implement the grid interactions of cables, piles, geogrids and liners (see Table 1). Only the linear and normal-yield springs are available for general use (see the structure link attach command). A normal-yield spring can be used to introduce plastic hinges between beam elements or pile elements (see Plastic Hinge Formation in a Beam Structure), and plastic-hinge lines along edges between shell-type elements (see Plastic Hinge Formation in a Shell Structure). The normal-yield spring provides elastic perfectly plastic behavior in both tension and compression, as well as the ability to track the formation of a gap that may form during yield in each direction.
| DOF | beam | cable | pile | shell | geogrid | liner |
|---|---|---|---|---|---|---|
| 1 | rigid | SY | SY | rigid | PY | PY |
| 2 | rigid | rigid | PY | rigid | PYDP | PYDP |
| 3 | rigid | rigid | PYDP | rigid | rigid | NY |
| 4 | free | free | free | free | free | free |
| 5 | free | free | free | free | free | free |
| 6 | free | free | free | free | free | free |
In Table 1, the symbols are defined as follows. “Rigid” means rigidly connected to the zone in which the element is embedded; “free” means that there is no connection in this degree of freedom. SY means shear-yield spring. PY and PYDP mean pile-yield and pile-yield dependent springs, which act together to produce the behavior of a single nonlinear spring acting in the plane defined by these two directions. NY means normal-yield spring. The nonlinear spring behaviors are not described here; instead, the overall element-to-grid interaction behavior of each element type that uses these springs is described in its own section.
A plastic hinge may be introduced between two nodes by creating a node-to-node link between the two nodes, aligning the node-local system for the target node such that a normal-yield spring can be inserted in the direction of the axis about which the hinge is to rotate, while all other directions are kept free (see Plastic Hinge Formation in a Beam Structure and Plastic Hinge Formation in a Shell Structure). The properties of the normal-yield spring should be set:
- Set the area equal to unity, and set the stiffness per unit area approximately ten times larger than the stiffness of the structural components using the node.
- Set the compressive- and tensile-yield strengths equal to the plastic-moment capacity (for beams and piles), or plastic-moment capacity per unit length (for shell-type elements).
The orientation of the node-local system is set automatically at the start of a set of cycles (or when the model cycle 0 command is executed), based on the type of elements that use the node (see Structural Element Nodes). When using the element creation commands (structure shell create etc.), if any of the nodes making up the newly created elements lie within zones, then node-to-zone links will be created and assigned the default attachment conditions shown in Figure 1:
Element-to-grid interaction occurs via node-to-zone links. These links store the zone, and an interpolation location within the zone, to allow transfer of forces and velocities between the nodes and the zones. By default, these interpolation locations will not change, even if running in large-strain mode. The interpolation locations can be allowed to migrate through the grid by setting the large-strain sliding flag of the link to on. Typically, one sets this flag to on for cables, piles, geogrids and liners, which then automatically set the flag to on for all links used by these elements. The migration process employs the large-strain sliding tolerance (see the tolerance options available to the structure link command).
Finite Element Stiffness Matrices
The structural response of each structural element is described by the stiffness that it provides to the surrounding system by means of its nodes. Each structural element has an associated stiffness matrix that is formed using finite-element techniques. The stiffness matrix \([\bf k]\) relates generalized nodal displacements (translations and rotations) \(\{\bf d \}\) to generalized nodal forces (forces and moments) \(\{\bf F \}\) by means of the relation \(\{ {\bf F} \} = [{\bf k}] \{ {\bf d} \}\), in which \([\bf k]\) is a square symmetric matrix of a size equal to the number of degrees of freedom associated with the finite element.
Six finite-element stiffness matrices have been implemented: a 2-noded beam finite element, and five 3-noded shell finite elements. These stiffness-matrix formulations are described in the following two subsections. Beam elements and pile elements utilize the beam finite element; cable elements utilize a degenerate form of the beam finite element in which only the local axially directed degrees-of-freedom are employed; and, shell elements, geogrid elements and liner elements utilize different shell finite elements. Note that the elements-to-grid interaction occurs by means of the links which connect the nodes used by elements to the zones.
Beam Finite Element
The beam finite element in the program is a two-noded, straight, finite element with six degrees of freedom per node: three translational components and three rotational components (see Beam Sign Convention). The beam finite element stiffness matrix formulation is given in explicit form by McGuire and Gallagher (1979, pp. 81-91). The element models the structural behavior of a beam that is straight, prismatic and symmetrical about both principal cross-sectional axes (bisymmetrical), and composed of isotropic material. The formulation considers displacements resulting from uniform axial deformation, flexural deformation, and twisting deformation. It neglects displacements resulting from transverse-shearing deformations, and displacements resulting from the out-of-plane (longitudinal) warping of a cross section that torsional forces may cause. According to McGuire and Gallagher, the equations embodied by the resulting stiffness matrix are sufficient for the analysis of the large majority of the frameworks encountered in structural-engineering practice.
Shell Finite Elements
There are five 3-noded, triangular finite elements available for shell-type elements: 2 plane-stress elements, 1 plate-bending element and 2 shell elements. The plane-stress elements model membrane action only, the plate-bending element models bending action only, and the shell elements model general shell behavior as a superposition of membrane and bending actions (see Bending Action and Membrance Action). These elements operate upon the 18 degrees of freedom available to the shell-type elements (see Shell-Type Coordinate System).
CST Plane-Stress Element (6 degrees of freedom)
The CST plane-stress element is a three-noded plane-stress finite element with two translational degrees-of-freedom per node (shown in Figure 3 (a) by removing the rotational degree-of-freedom). The CST hybrid element is described, and an explicit formulation of \([{\bf k}_{\rm CST}]\) is given by Cook et al. (1989).
CST Hybrid Plane-Stress Element (9 degrees of freedom)
The CST hybrid plane-stress element is a three-noded plane-stress finite element with three degrees of freedom per node: two translational components and one rotational component (shown in Figure 3 (a)). The CST hybrid plane-stress element is formulated by the assumed-stress hybrid approach. It provides a more competent membrane response than a constant strain triangle (CST) through the inclusion of “drilling freedoms,” \(\theta_z\), among its degrees of freedom. The CST hybrid element is described, and an explicit formulation of \([{\bf k}_{\rm CSTH}]\) is given by Cook (1987).
DKT Plate Bending Element (9 degrees of freedom)
The DKT plate bending element is a three-noded plate finite element with three degrees of freedom per node: one translational component and two rotational components (shown in Figure 3 (b)). The DKT plate bending element enforces the Kirchhoff plate theory assumptions at six discrete locations (corners and mid-sides) within the element; thus, the designation DKT for Discrete Kirchhoff Triangle. The element is described by Batoz et al. (1980), who conclude that it is one of the most efficient and reliable three-node (9 degrees of freedom) plate bending elements available at the time of publication. An explicit formulation of \([{\bf k}_{\rm DKT}]\) is given by Batoz (1982).
DKT-CST Hybrid Shell Element (18 degrees of freedom)
The DKT-CST hybrid shell element is a three-noded, flat, thin-shell finite element with six degrees of freedom per node: three translational components and three rotational components. It combines a nine degrees-of-freedom CST hybrid plane element to model membrane action in the shell with a nine degrees-of-freedom DKT plate element to model bending action in the shell. This composite flat shell element is referred to as a DKT-CST hybrid, and is described by Cook et al. (1989, pp. 351-352).
Let a typical element lie in the \(xy\)-plane of a local coordinate system \(xyz\). Nodal degrees-of-freedom are shown in Figure 3, where \(\lfloor \theta_x \quad \theta_y \rfloor = \lfloor {\partial w \over \partial y} \quad -{\partial w \over \partial x} \rfloor\). Let these degrees of freedom be called \(\{{\bf d'} \}\), and be arranged in the order
where \(\lfloor {\bf u}_i \rfloor = \lfloor u_1\quad u_2 \quad u_3 \rfloor\), \(\lfloor {\bf\theta}_{xi} \rfloor = \lfloor \theta_{x1}\quad \theta_{x2} \quad \theta_{x3} \rfloor\), and so on. For the DKT-CST hybrid shell element, whose stiffness matrix in local \(xyz\)-coordinates is called \([{\bf k'}]\), we have
where \([{\bf k}_{\rm CSTH}]\) is the stiffness matrix of a CST hybrid plane-stress element, and \([{\bf k}_{\rm DKT}]\) is the stiffness matrix of a DKT plate-bending element.
The following observations about the DKT-CST hybrid element are appropriate (also see the observations about the DKT-CST element in the next section).
- \([{\bf k}_{\rm CSTH}]\) only contains degrees of freedom associated with membrane action, and \([{\bf k}_{\rm DKT}]\) only contains degrees of freedom associated with bending action. Although membrane-bending coupling is present throughout an actual curved shell, it is absent in an individual element (as evidenced by the 9 by 9 null matrices of (1)). Nevertheless, the element works well enough to be competitive with curved elements, as demonstrated by Carpenter et al. (1986).
- The element provides a solution which converges to the classical Kirchhoff thin-plate solution. Thus, the element is appropriate for modeling thin shells in which the displacements caused by transverse-shearing deformations can be neglected.
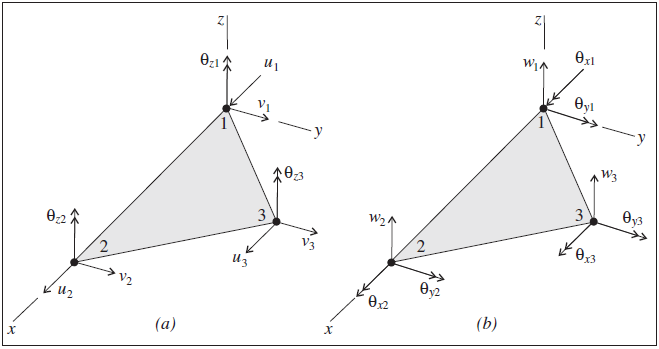
Figure 3: DKT-CST hybrid flat shell finite element in a local xy-plane: (a) degrees of freedom associated with membrane action (CST hybrid sub-element); (b) degrees of freedom associated with bending action (DKT sub-element)
DKT-CST Shell Element (15 degrees of freedom)
The DKT-CST shell element is a three-noded, flat, thin-shell finite element with five degrees of freedom per node: three translational components and two rotational components. It combines a six degrees-of-freedom CST plane element to model membrane action in the shell with a nine degrees-of-freedom DKT plate element to model bending action in the shell. This composite flat shell element is referred to as a DKT-CST, and is described by Cook et al. (1989, pp. 351-352).
Let a typical element lie in the \(xy\)-plane of a local coordinate system \(xyz\). Nodal degrees-of-freedom are shown in Figure 3 by removing \(\theta_z\), where \(\lfloor \theta_x \quad \theta_y \rfloor = \lfloor {\partial w \over \partial y} \quad -{\partial w \over \partial x} \rfloor\). Let these degrees of freedom be called \(\{{\bf d^\star} \}\), and be arranged in the order
where $lfloor {bf u}_i rfloor = lfloor u_1quad u_2 quad u_3 rfloor$, $lfloor {ubmtheta}_{xi} rfloor = lfloor theta_{x1}quad theta_{x2} quad theta_{x3} rfloor$, and so on. For the DKT-CST shell element, whose stiffness matrix in local $xyz$-coordinates is called $[{bf k^star}]$, we have
where \([{\bf k}_{\rm CST}]\) is the stiffness matrix of a CST plane-stress element, and \([{\bf k}_{\rm DKT}]\) is the stiffness matrix of a DKT plate bending element.
The following observations about the DKT-CST element are appropriate.
- \([{\bf k}_{\rm CST}]\) only contains degrees of freedom associated with membrane action, and \([{\bf k}_{\rm DKT}]\) only contains degrees of freedom associated with bending action. Although membrane-bending coupling is present throughout an actual curved shell, it is absent in an individual element (as evidenced by the null matrices of (2).
- The element provides a solution which converges to the classical Kirchhoff thin-plate solution. Thus, the element is appropriate for modeling thin shells in which the displacements caused by transverse-shearing deformations can be neglected.
- The element differs from the DKT-CST hybrid element by not having drilling degrees-of-freedom. This makes the element overly stiff for problems with large membrane-stress gradients. For such problems, the DKT-CST hybrid element will perform better. For problems without large membrane-stress gradients, the performance of the DKT-CST element will be much improved, making it competitive with the DKT-CST hybrid element.
- The lack of drilling degrees-of-freedom makes this element more suitable for coupling with the model grid than the DKT-CST hybrid element. The zones have a linear displacement variation, and the 3 drilling degrees-of-freedom give the DKT-CST hybrid a quadratic in-plane displacement variation along its edges. When a shell-type element is rigidly connected to the grid, only the translational degrees-of-freedom are slaved to move with the grid, while the rotational degrees-of-freedom are left free. Because we are not constraining the drilling degrees-of-freedom, it is possible for gaps to form between the element and the grid. These incompatibilities seem to be activated when shell-type elements of different sizes meet along a common line. The DKT-CST element has a linear in-plane displacement variation along its edges, which is fully compatible with that of the zones and, thus, gaps cannot form when these elements are rigidly connected to zones.
- The two preceding observations lead to the following general recommendation regarding choice of shell finite element. For problems in which a shell element is being connected to zones, use the DKT-CST element. For all other problems, use the DKT-CST hybrid element.
Stress Recovery Procedure
The stress-recovery procedure is outlined in Stress Recovery Procecure. A more detailed description of the process is provided here. Stress recovery is applied to a group of shell-type elements. Nodal averaging of bending and membrane stress resultants only occurs for elements within this group. Stress recovery consists of two steps:
Compute stress-resultant field.
Define the surface coordinate system at each node.
This system has its \(z\)-direction equal to the average \(z\)-direction of all shell-type elements using the node, and has its \(x\)-direction equal to the projection of a user-specified surface vector onto the \(z\)-plane.
Compute the bending and membrane stress resultants
(\(M_x\), \(M_y\), \(M_{xy}\), \(N_x\), \(N_y\), and \(N_{xy}\)) at each node. These values are found by first computing them within each shell-type element at its nodes, and then averaging the contributions from all shell-type elements that use each node.
Note that these six stress resultants vary linearly over each element.
The bending and membrane stress resultants within each shell-type element are found using the flexibility-stiffness transformation from McGuire and Gallagher (1979, pp. 76-77) to determine which displacements are consistent with a given set of nodal forces acting on the element. This is done by forming a flexibility matrix that is derived from the element stiffness matrix. The flexibilities are derived from the stiffnesses by defining a stable, statically determinate support system, removing from the stiffness matrix the rows and columns corresponding to the support components, and inverting the remainder. These displacements are then fed into stress-recovery procedures appropriate to the particular finite element.
Compute the transverse-shear stress resultants (\(Q_x\) and \(Q_y\)) within each shell-type element by enforcing the equilibrium equations
\[ \begin{align}\begin{aligned}Q_x = {\partial M_x \over \partial x} + {\partial M_{xy} \over \partial y}\\Q_y = {\partial M_y \over \partial y} + {\partial M_{xy} \over \partial x}\end{aligned}\end{align} \]by assuming that the bending resultant field varies linearly over each element. Note that \(Q_x\) and \(Q_y\) are constant over each shell-type element, and are not averaged at nodes.
Compute stress field at specified shell depth using Stresses From Resultants, and then rotating the stresses into the global system.
Governing Equations
The discretization and time integration of the equations that govern the dynamic response of the structural elements and their associated entities (i.e., nodes and links) utilize standard finite-element practice. The description given here is similar to that given in Chapter 13 of Cook et al. (1989).
The equations that govern the dynamic response of a structure can be derived by requiring the work of external forces to be absorbed by the work of internal, inertial and damping forces for any small, kinematically admissible motion. For a single element, this work balance becomes
where \(\{ \delta {\bf u} \}\) and \(\{ \delta {\bf \epsilon} \}\) are, respectively, small arbitrary displacements and their corresponding strains, \(\{ {\bf F} \}\) are body forces, \(\{ {\bf \Phi} \}\) are prescribed surface tractions that act over a portion of the element surface \(S_e\), \(\{ {\bf p}_i \}\) are concentrated loads that act at a total of \(n\) points on the element, \(\{ {\bf u} \}_i^T\) is the displacement of the point at which load \(\{ {\bf p}_i \}\) is applied, \(\{ {\bf \sigma} \}\) are stresses, \(\rho\) is the mass density of the material, \(\kappa_d\) is a material-damping parameter analogous to viscosity, and volume integration is carried out over the element volume, \(V_e\).
If we express the displacement field \(\{ {\bf u} \}\) (which is a function of both space and time) and its first two time derivatives as
where shape functions \([{\bf N}]\) are functions of space only, and nodal degrees-of-freedom \(\{{\bf d}\}\) are functions of time only, then (4) represent a local separation of variables. By substituting (4) into (3), and noting that \(\{ \delta{\bf u} \}\), and thus \(\{ \delta{\bf d} \}\), are arbitrary, one obtains
where the element mass and damping matrices are defined as
and the element internal force and external load vectors are defined as
where \([{\bf B}]\) is the strain-displacement matrix that satisfies \(\{\delta {\bf \epsilon}\} = [{\bf B}]\{{\bf d}\}\).
(5) is a system of coupled, second-order, ordinary differential equations in time, and is called a finite-element semi-discretization because, although displacements \([{\bf d}]\) are discrete functions of space, they are still continuous functions of time. The structural-element logic employs an explicit, direct-integration method which discretizes (5) in time, using the central-difference method to obtain a sequence of uncoupled algebraic equations.
Recall that (5) was written for a single element. Equations for the assembled structural system can be written as
where \(\{{\bf A}\}\) designates the accumulated out-of-balance force, and uppercase English alphabet characters designate structure matrices which are constructed by the conceptual expansion of element matrices to “structure size,” followed by addition of overlapping coefficients. See any standard finite-element text (e.g., Cook et al. 1989) for a detailed description of the assembly procedure.
The equations of motion, (9), are written for a specific instant of time:
where subscript \(n\) denotes time \(n\Delta t\), and \(\Delta t\) is the size of the time increment or timestep.
Central-Difference Approximations
The central-difference approximations for acceleration at time \(n\Delta t\), velocity at time \((n - {\scriptstyle 1/2})\Delta t\), and velocity at time \(n\Delta t\) are given by
These expressions are second-order accurate, which implies that halving the timestep should approximately quarter the error in the approximation.
Accumulated Out-of-Balance Force Vector
The structure internal force vector that makes up one portion of the accumulated out-of-balance force vector \(\{{\bf A}\}_n\) in (10) is obtained by assembling the contributions from each structural element and from each deformable direction of each link
with
in which the central-difference approximation of (12) has been employed. The internal-force vector \(\{ {\bf r}^{\rm int} \}\) that is maintained by each structural element and each deformable direction of each link is also updated during the computation of \(\{ {\bf R}^{\rm int} \}\).
After distributing all of the internal forces to the appropriate nodes, each rigidly attached direction, \({\bf n}^{[{\rm S}]}\), of each link contributes the following portion of the accumulated out-of-balance force of its source node \({\bf A}^{[{\rm S}]}\) to the accumulated out-of-balance force \({\bf A}^{[{\rm T}]}\) of its target entity as
Mass Matrix
The structure mass matrix in (10) is obtained by utilizing a nodal-lumping scheme, and assembling the contributions from each structural element
with
where \(\rho_j\), \(V_j\) and \(n_j\) are the mass density, volume and number of nodes of element \(j\). The rotational inertias are found by assuming that the portion of element mass seen by each node is distributed as a sphere.
After distributing the mass associated with all of the structural elements to the appropriate nodes, each rigidly attached direction of each link contributes the following portion of its source mass in direction- \(k\) \(m_k^{[{\rm S}]}\) to the accumulated mass in target direction-\(i\) \(m_i^{[{\rm T}]}\), using the weighting function
where \({\bf n}_i^{[{\rm S}]}\) and \({\bf n}_i^{[{\rm T}]}\) are, respectively, the unit-vector triads of the source and target local coordinate systems.
Damping Formulation
The derivation of equation (6) utilized a viscous-damping parameter that is suitable for modeling a Newtonian fluid; however, when modeling structural systems, we are less interested in viscous damping than in dry friction and hysteresis loss. These energy-loss mechanisms are not well-understood and, from a practical standpoint, (6) does not correctly represent structural damping. Thus, three ad hoc damping schemes (local damping, combined local damping and Rayleigh or proportional damping) are provided. The implementation details of the three damping schemes are presented here; refer to Mechanical Damping and Rayleigh Damping for a description of the rationale behind each scheme.
The starting point for all three damping schemes is given by rewriting (10) as
where \(\{ {\bf R}^{\rm d} \}_n\) represents the force produced by the damping mechanism at time \(n\Delta t\).
Local Damping
Substitution of (11) into (15) yields
The use of a diagonal mass matrix (as described in Mass Matrix) uncouples this set of equations such that we can rewrite them for a single degree of freedom \(i\) as
Local damping is provided by setting
where \(\lambda_i\) is the local-damping factor for degree-of-freedom \(i\), and
The local-damping formulation is implemented by computing an undamped \((\dot D_i )^{\rm ud}\) and a damped \(( \dot D_i )^{\rm d}\) new velocity:
and setting the actual new velocity equal to the damped velocity (only if the velocity has not changed sign) as
It can be shown that this implementation maintains second-order accuracy as follows. Assume that
This implies that
which makes (18) an exact expression of (17). Note that if the assumption of (19) is not satisfied (i.e., the velocity either changes sign or is zero), then no damping is applied to this degree of freedom.
Combined Local Damping
Combined local damping is provided by utilizing the same procedure as described for local damping, but with (17) replaced by
where
Rayleigh Damping
Rayleigh damping results by forming the damping matrix \([ {\bf C} ]\) as a linear combination of the stiffness and mass matrices:
where \(\beta\) and \(\alpha\) are called, respectively, the stiffness- and mass-proportional damping constants. The relation between \(\beta\), \(\alpha\) and the fraction of critical damping \(\xi\) at frequency \(\omega\) is given by
Damping attributable to stiffness increases with increasing frequency, whereas damping attributable to mass increases with decreasing frequency.
Damping constants \(\beta\) and \(\alpha\) are related to the fractions of critical damping (\(\xi_1\) and \(\xi_2\)) at frequencies (\(\omega_1\) and \(\omega_2\)) by
The governing equation of motion used when Rayleigh damping is active is derived as follows. Express the force produced by the damping mechanism (\(\{ {\bf R}^{\rm d} \}_n\) in (15)) as the sum of the stiffness and mass contributions:
and substitute this expression into (15) to obtain
Substitution of the central-difference approximations given by (11) and (13) into (20), followed by rearrangement of terms, yields
in which the stiffness contribution to the damping force is obtained by assembling the contributions from each structural element and from each deformable direction of each link:
with
Computation of Stable Timestep
Time integration carried out using the central-difference method is a conditionally stable process. The stable timestep for our central-difference equations ((16) if local or combined local damping is active, or (20) if Rayleigh damping is active) is given by (Belytschko 1983)
where \(\omega_{\rm max}\) is the highest natural frequency of the discretized system, and \(\xi_{\rm max}\) is the fraction of critical damping at \(\omega_{\rm max}\). The value of \(\xi_{\rm max}\) is dependent upon the damping scheme,
The natural frequencies, \(\omega_n\), of the discretized system are given by solution of the eigenproblem,
The maximum frequency can be bounded by applying Gerschgorin’s Theorem (Isaacson and Keller 1963) to (26) which, for a diagonal mass matrix, states that
where \(n_e\) is the number of degrees of freedom, and \(G_i\) is the stiffness sum for the \(i\)th row of the assembled stiffness matrix
The six components of \(G_i\) are stored at each structural-element node and expressed in terms of the node-local system. Stiffness contributions are provided by all structural elements and by all deformable directions of all links. After distributing all of the stiffnesses to the appropriate nodes, each rigidly attached direction of each link contributes the following portion of its source stiffness in direction-\(k\) \(G_k^{[{\rm S}]}\) to the accumulated stiffness in target direction-\(i\) \(G_i^{[{\rm T}]}\), using the same weighting function as given by (14), namely
where \({\bf n}_i^{[{\rm S}]}\) and \({\bf n}_i^{[{\rm T}]}\) are, respectively, the unit-vector triads of the source and target local coordinate systems.
The final timestep computed by the structural-element portion of the program is
where \(\beta_u\) is a user-specified safety factor, and \(\Delta t_{\rm stab}\) is computed using (24), (25) and (27), in which (27) is only applied to active degrees-of-freedom.
Mass Scaling
The structural-element portion of the program may be run in one of three modes (fully dynamic, fully static or partially dynamic):
- When run in the fully dynamic mode (
structure scale-rotational-massoff), mass scaling is not applied; instead, the mass matrix reflects the actual mass of the structural system and is assembled as described in Mass Matrix. The timestep necessary to ensure a stable integration of the equations of motion is determined as described in Computation of Stable Timestep. - When run in the fully static mode, the values in the mass matrix are adjusted to ensure that all degrees of freedom have the same frequency response — one that is appropriate to ensure a stable integration of the equations of motion for a fixed value of timestep. The procedure by which this is accomplished is described below.
- When run in the partially dynamic mode (
structure scale-rotational-masson), the mass matrix reflects the actual mass of the translational degrees-of-freedom, and only the translational degrees-of-freedom are considered when determining the timestep necessary to ensure a stable integration of the equations of motion. The masses of the rotational degrees-of-freedom are adjusted to ensure that all rotational degrees-of-freedom have the same frequency response — one that is appropriate to ensure a stable integration of the equations of motion for the fixed value of timestep determined for the translational degrees-of-freedom. The procedure by which this is accomplished is described below.
Fully Static Mode
For a given value of timestep \(\Delta\tilde t\), stability requires that
where the estimated stable timestep has been multiplied by a safety factor of one-half.
By setting the maximum frequency equal to its bounding value provided by (27), one can write
in which \(\psi\) has been introduced to represent the second term. One can ensure that all degrees of freedom have the same frequency response by setting each \(M_i\) such that
\(\psi\) can be computed directly because \(\xi_{\rm max}\) is given by (25).
Partially Dynamic Mode
Set all translational masses using the procedure described in Mass Matrix.
Determine the timestep necessary to ensure a stable integration of the equations of motion by only considering the translational degrees-of-freedom when using the procedure described in Computation of Stable Timestep.
Determine the highest natural frequency of the discretized system by applying (27) to only the translational degrees-of-freedom, and call this value \(\omega^\star\). Set all masses associated with rotational degrees-of-freedom such that they satisfy
\[M_i = G_i / {\omega^\star}^2\]in order to ensure that the rotational degrees-of-freedom do not produce a larger natural frequency than \(\omega^\star\).
Computational Algorithm
- Assume that boundary conditions consisting of externally applied loads, \(\{{\bf R}^{\rm ext}\}\), as well as structural element, link and nodal properties have been specified.
- Set initial conditions:
Assemble the structure mass matrix \(\lceil {\bf M} \rfloor\) by considering the mode in which the structural-element portion of the program is being run. For the fully dynamic case, employ the procedure described in Mass Matrix. For the fully static or partially dynamic cases, employ the procedures described in Mass Scaling.
Compute stable timestep \(\Delta t\), as described in Computation of Stable Timestep.
Compute the accumulated out-of-balance force vector \(\{ {\bf A} \}_n\):
- Set \(\{ {\bf A} \}_n = \{ {\bf R}^{\rm ext} \}_n\).
- Assemble the contributions from each structural element, each deformable direction of each link, and each rigidly attached direction of each link, as described in Accumulated Out-of-Balance Force Vector.
- If Rayleigh damping is active, assemble the stiffness contribution to the damping force \(\{ {\bf R}^{\beta} \}_n\) using (22) and (23).
Update all nodal velocities \(\{ \dot{\bf D} \}_{n \scriptscriptstyle + 1/2}\):
- For all active degrees-of-freedom (i.e., those that are not fixed and are not slaved), update velocities using (16) if local or combined local damping is active, or (20) if Rayleigh damping is active.
- For each rigidly attached direction \({\bf n}^{[{\rm S}]}\) of each link, set velocity of source node \(\dot{\bf D}^{[{\rm S}]}\) equal to component of velocity of target entity in the attached direction: \(\quad\dot{\bf D}^{[{\rm S}]} = \left( \dot{\bf D}^{[{\rm T}]} \cdot {\bf n}^{[{\rm S}]} \right) {\bf n}^{[{\rm S}]}\)
Update all nodal positions. Each node stores:
- its reference position \({\bf x}^{\rm ref}\), which corresponds to its position at the time that all related stiffness matrices were formed,
- its current position \({\bf x}^{\rm cur}\), and
- its accumulated rotation \({\bf \theta}^{\text{cur}}\) since the last update of \({\bf x}^{\text{ref}}\).
The displacement that has occurred since the last update of \({\bf x}^{\text{ref}}\) is given by
\[\begin{split}\begin{Bmatrix} {\bf d} \end{Bmatrix} = \begin{Bmatrix} {\bf d}^{\text{tran}} \\ {\bf d}^{\text{rot}} \end{Bmatrix} = \begin{Bmatrix} {\bf x}^{\text{cur}} - {\bf x}^{\text{ref}} \\ {\bf \theta}^{\text{cur}} \end{Bmatrix}\end{split}\]and the current positions and rotations are updated using the central-difference approximation of (12):
\[ \begin{align}\begin{aligned}\begin{Bmatrix} {\bf x}^{\text{cur}} \end{Bmatrix}_{n+1} = \begin{Bmatrix} {\bf x}^{\text{cur}} \end{Bmatrix}_n + \begin{Bmatrix} {\bf \dot{d}}^{\text{tran}} \end{Bmatrix}_{n+1/2} \Delta t\\\begin{Bmatrix} {\bf \theta}^{\text{cur}} \end{Bmatrix}_{n+1} = \begin{Bmatrix} {\bf \theta}^{\text{cur}} \end{Bmatrix}_n + \begin{Bmatrix} {\bf \dot{d}}^{\text{rot}} \end{Bmatrix}_{n+1/2} \Delta t\end{aligned}\end{align} \]Update all structural element stiffness matrices if a large-strain update is due; otherwise, set
\[[{\bf k}]_{n \scriptscriptstyle + 1/2} = [{\bf k}]_{n \scriptscriptstyle - 1/2} \; \text{for all elements}\]Set \(n \leftarrow n + 1\), and go to step 3.
References
AISC. Manual of Steel Construction, Eighth Edition. Chicago: American Institute of Steel Construction Inc. (1980).
Batoz, J. L. “An Explicit Formulation for an Efficient Triangular Plate-Bending Element,” Int. J. Num. Meth. Engng., 18(7), 1077-1089 (1982).
Batoz, J. L., K. J. Bathe and L. W. Lo. “A Study of Three-Node Triangular Plate Bending Elements,” Int. J. Num. Meth. Engng., 15(12), 1771-1812 (1980).
Belytschko, T. “An Overview of Semidiscretization and Time Integration Procedures,” in Computational Methods for Transient Analysis, Chapter 1, pp. 1-65. T. Belytschko and T. J. R. Hughes, eds. New York: Elsevier Science Publishers, B. V. (1983).
Beneito, C. and Ph. Gotteland. “Three-Dimensional Numerical Modeling of Geosynthetics Mechanical Behavior,” in FLAC and Numerical Modeling in Geomechanics (Proceedings of the Second International FLAC Symposium on Numerical Modeling in Geomechanics, Lyon, France, 29-31 October 2001). D. Billaux et al., eds. Lisse: Balkema (2001).
Carpenter, N., H. Stolarski and T. Belytschko. “Improvements in 3-Node Triangular Shell Elements,” Int. J. Num. Meth. Engng., 23(9), 1643-1667 (1986).
Cernica, J. N. Geotechnical Engineering: Foundation Design, New York: John Wiley & Sons Inc. (1995).
Clayton, C. R. I., J. Milititsky and R. T. Woods. Earth Pressure and Earth-Retaining Structures, pp. 145-148. London: Blackie Academic & Professional (1993).
Cook, R. D. “A Plane Hybrid Element with Rotational D. O. F. and Adjustable Stiffness,” Int. J. Num. Meth. Engng., 24(8), 1499-1508 (1987).
Cook, R. D., D. S. Malkus and M. E. Plesha. Concepts and Applications of Finite Element Analysis, Third Edition. New York: John Wiley & Sons Inc. (1989).
Isaacson, E., and H. B. Keller. Analysis of Numerical Methods, pp. 135-136. New York: John Wiley & Sons Inc. (1963).
Massonnet, C. E. Résistance Des Matériaux. Sciences Et Lettres, Liége (1960).
McGuire, W., and R. H. Gallagher. Matrix Structural Analysis. New York: John Wiley & Sons Inc. (1979).
St. John, C. M., and D. E. Van Dillen. “Rockbolts: A New Numerical Representation and Its Application in Tunnel Design,” in Rock Mechanics — Theory - Experiment - Practice (Proceedings of the 24th U.S. Symposium on Rock Mechanics, Texas A&M University, June 1983), pp. 13-26. New York: Association of Engineering Geologists (1983).
Ugural, A. C. Stresses in Plates and Shells, pp. 1-16. New York: McGraw-Hill Publishing Company Inc. (1981).
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |