Oedometer Test with Plastic-Hardening Model
Note
To view this project in FLAC3D, use the menu command . Choose “ConstitutiveModels/ OedometerPlasticHardening” and select “OedometerPlasticHardening.prj” to load. The project’s main data file is shown at the end of this example.
This section presents the simulation of an oedometer test to reveal the capability of the Plastic-Hardening (PH) model to reproduce the evolution of lateral stress ratio \(K_0 = \sigma_h/\sigma_h\). Three kinds of sands with friction angles of 30, 35, and 40 degrees are used in the simulations of this case (Case 1) and the default consolidation coefficient is calculated as \(K_{nc} = 1 − \sin \phi\). The model properties are listed in Table 1. The properties not listed in the table are using the default values. Initially the model is in equilibrium with isotropic stress state in each zone, \(\sigma_1\) = \(\sigma_2\) = \(\sigma_3\) = −1 kPa.
| Parameter | Dense | Medium | Loose |
|---|---|---|---|
| \(E^{ref}_{50}\) (kPa) | 4.0e4 | 3.0e4 | 2.0e4 |
| \(\phi\) | 40 | 35 | 30 |
| \(\psi\) | 10 | 5 | 0 |
| \(K_{nc}\) (Case 2) | 0.7 | 0.6 | 0.5 |
| \(p_{ref}\) (kPa) | 100.0 | ||
| \(m\) | 0.5 | ||
| \(\sigma^{ini}_{1 \sim 3}\) (kPa) | -1.0 | ||
| \(OCR\) | 1.0 |
The results of stress ratio evolution due to compression in the oedometer tests are shown in Figure 1, and it is seen that they correctly reproduce the expected evolution path. Figure 2 presents vertical oedometer pressure versus vertical strain. The slope of the curves at the specified reference pressure of 100 kPa reproduces the expected oedometer stiffness (as \(E^{ref}_{oed}\) is not provided as part of input, it is assigned to the same as \(E^{ref}_{50}\) by default; see the property section of the PH model).
The test is repeated in Case 2 using predefined values of \(K_{nc}\) = 0.7, 0.6, and 0.5, respectively. The results for \(K_0\) are plotted in Figure 3 and Figure 4 shows variation of vertical oedometer pressure versus axial strain. Again, correct stress paths and oedometer stiffness at the reference vertical pressure are successfully reproduced.
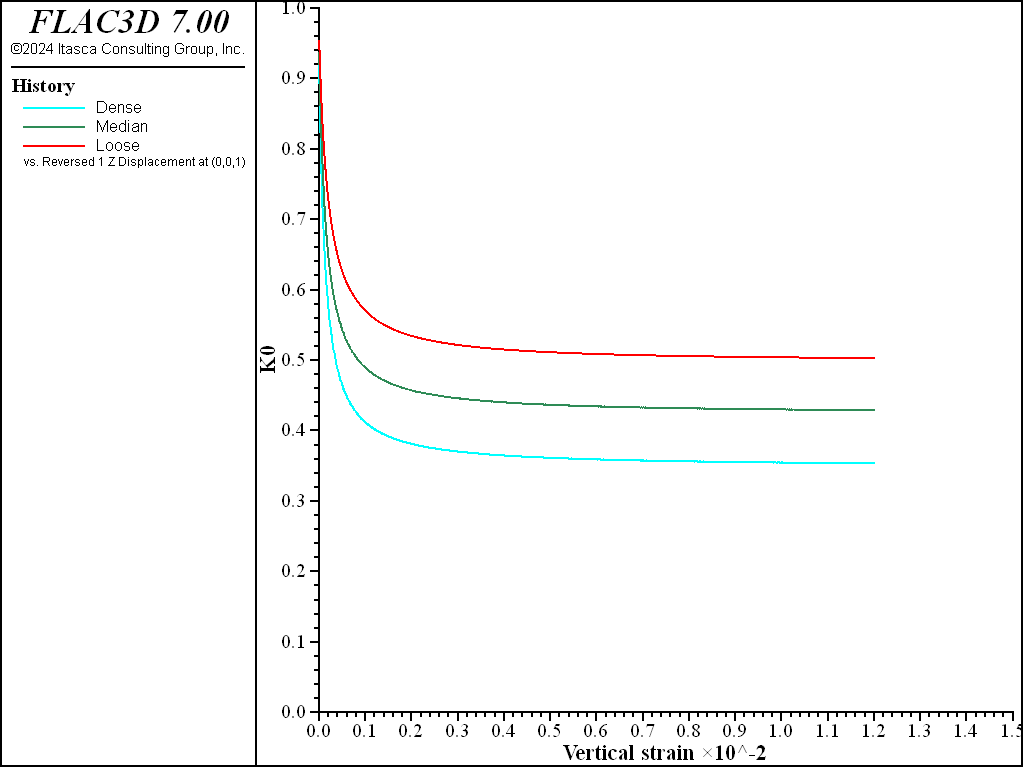
Figure 1: \(K_0\) path calculated from the oedometer test with friction angles of 30, 35, and 40 degrees and default \(K_{nc}\) values.
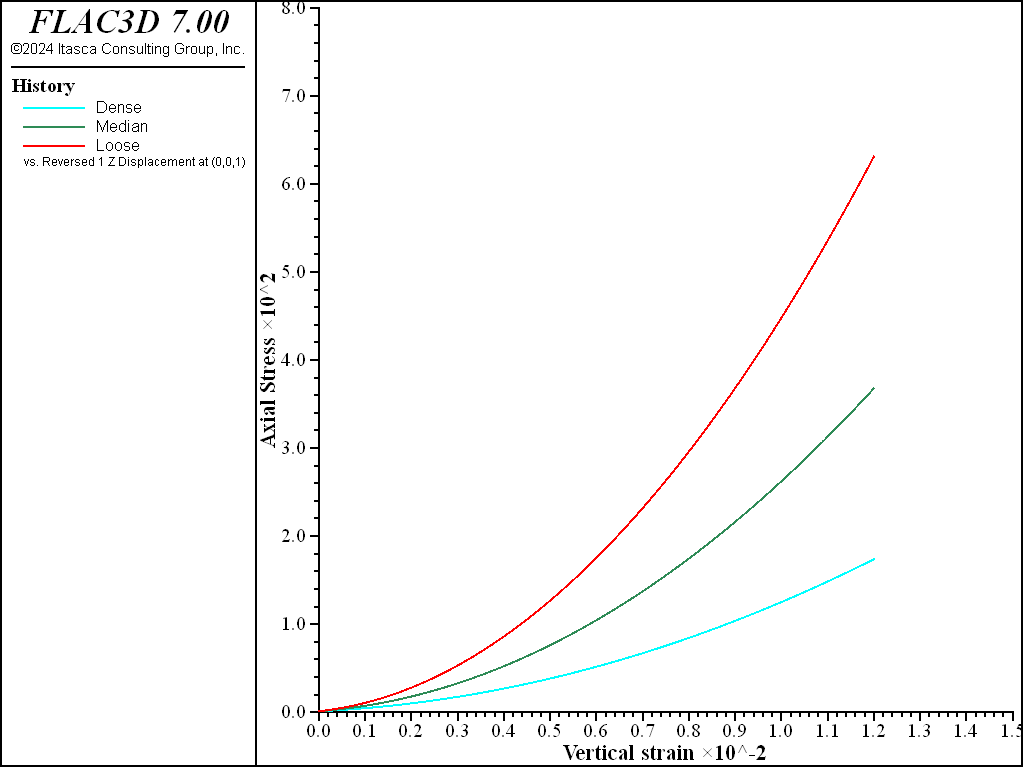
Figure 2: Vertical pressure versus vertical strain from the oedometer test with friction angles of 30, 35, and 40 degrees and default \(K_{nc}\) values.
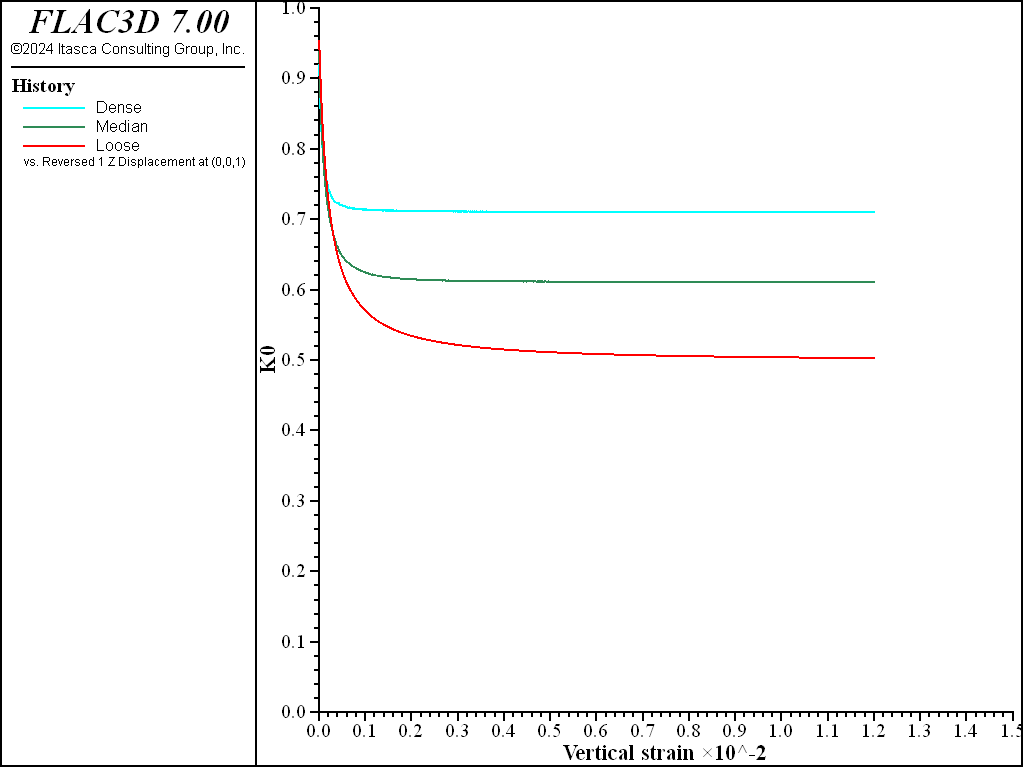
Figure 3: \(K_0\) path calculated from the oedometer test with friction angles of 30, 35, and 40 degrees and specified \(K_{nc}\) values.
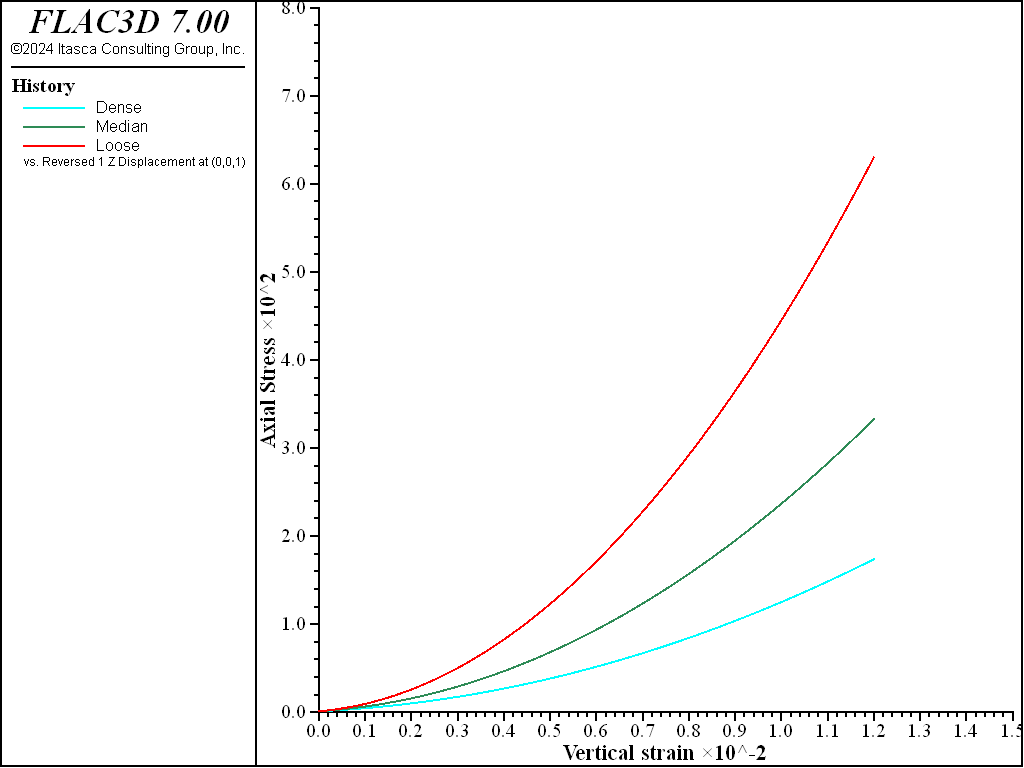
Figure 4: Vertical pressure versus vertical strain from the oedometer test with friction angles of 30, 35, and 40 degrees and specified \(K_{nc}\) values.
Data File
OedometerPlasticHardening.dat
model large-strain off
zone create brick size 1 1 5
zone cmodel assign plastic-hardening
zone prop dens 1000 pressure-reference=100. exponent=0.5 ...
over-consolidation-ratio=1.0 factor-cut 0.01
zone prop stress-1-effective=-1 stress-2-effective=-1 stress-3-effective=-1
zone prop stiffness-50-reference=4e4 friction=40. dilation=10. ...
coefficient-normally-consolidation=[_Knc1] range id 1
zone prop stiffness-50-reference=3e4 friction=35. dilation= 5. ...
coefficient-normally-consolidation=[_Knc2] range id 3
zone prop stiffness-50-reference=2e4 friction=30. dilation= 0. ...
coefficient-normally-consolidation=[_Knc3] range id 5
zone cmodel assign null range id-list 2 4
;
zone gridpoint fix velocity
zone face apply velocity-z -1e-6 ...
range union position-z 1 position-z 3 position-z 5
zone initialize stress xx -1 yy -1 zz -1
;
[global _z15 = zone.near(0.5, 0.5, 4.5)]
[global _z13 = zone.near(0.5, 0.5, 2.5)]
[global _z11 = zone.near(0.5, 0.5, 0.5)]
fish def _k0_d
global _k0_l = 0.5*(z.s.xx(_z15)+z.s.yy(_z15)) / z.s.zz(_z15)
global _k0_m = 0.5*(z.s.xx(_z13)+z.s.yy(_z13)) / z.s.zz(_z13)
global _k0_d = 0.5*(z.s.xx(_z11)+z.s.yy(_z11)) / z.s.zz(_z11)
end
zone history displacement-z position 0 0 1
zone history stress-zz position 0.5 0.5 4.5
zone history stress-zz position 0.5 0.5 2.5
zone history stress-zz position 0.5 0.5 0.5
fish history _k0_d
fish history _k0_m
fish history _k0_l
history interval 10
;
model step 12000
model save [string.build('oed%1', _ICase)]
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |
