Cyclic Undrained DSS Tests with P2PSand Model
Note
To view this project in FLAC3D, use the menu command . Choose “Dynamic/ CyclicUndrainedDirectSimpleShear” and select “CyclicUndrainedDirectSimpleShear.prj” to load. The main data files used are shown at the end of this example. The remaining data files can be found in the project.
One-zone numerical tests of undrained cyclic direct simple shear (DSS) loading responses are performed. All these tests are starting from an initial effective vertical stress (\(\sigma^{\prime}_{v0}\)) along z-axis at 100 kPa (around 1 atm), \(K_0=0.5\), and zero initial static shear stresses. All parameters are with the default parameters except the initial relative densities are different. Pore-pressure in the zone is allowed for building-up. The out-of-plane (alone y-axis) strains are restricted. The degrees-of freedom at the zone top are attached so that all grid points at the top have the same displacements to satisfy the DSS conditions. The gridpoints at the zone top are velocity-controlled. Once the shear stress (\(\tau\)) amplitude reaches a certain value (\(CSR \times \sigma^{\prime}_{v0}\)), the velocities of gridpoints at the zone top will be reverted. In this example, the parameter study is performed by a Python-based master file.
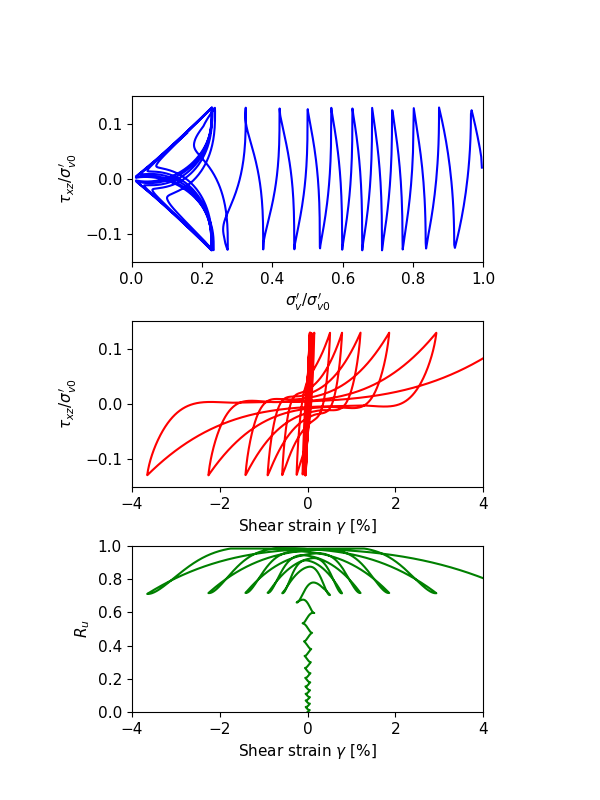
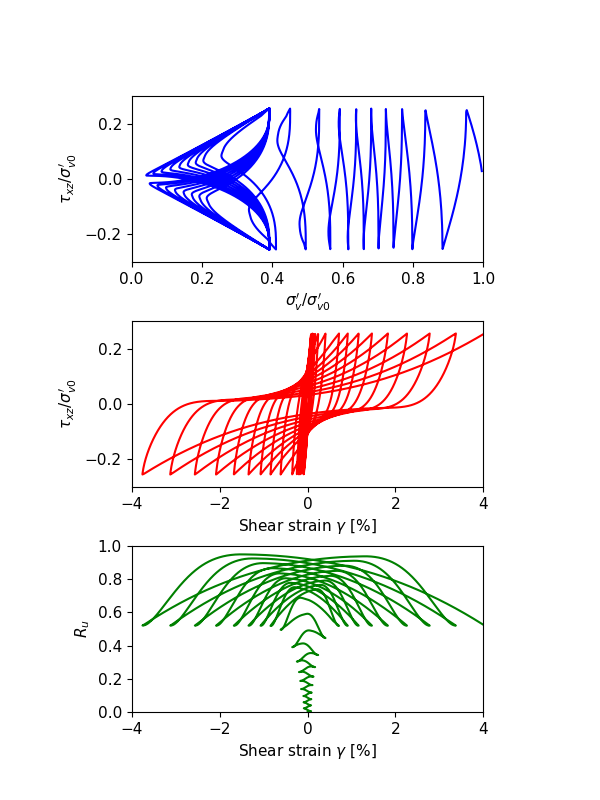
The numerical results of undrained cyclic DSS loading responses with the relative density at \(D_r\) = 0.3, 0.5 and 0.7, are illustrated in Figure 1, 2 and 3, to represent relative loose, median dense and dense sands, respectively. In each of the figures, the top sub-figure is plotting \(\sigma^{\prime}_v/\sigma^{\prime}_{v0}\) versus \(\tau_{xz}/\sigma^{\prime}_{v0}\), the center sub-figure is plotting \(\sigma^{\prime}_v/\sigma^{\prime}_{v0}\) versus \(\gamma\), and the bottom sub-figure is plotting \(R_u\) versus \(\gamma\). All illustrated responses reach about \(\gamma = 3\%\) (S.A.) shear strain with the fitted CSR values at approximately 15 cycles. The shear stress - shear strain responses illustrate shear strain progresses even after the excess pore pressure ratio (\(R_u\)) reaches 99%.
For relatively loose sands as shown in Figure 1, the shear strain increases to a very small value at the first several cycles. After dilatancy surface has been hit, the shear strain dramatically increases to around 3% \(\sigma^{\prime}_v\) is close to 0, and \(R_u\) is close to 1, merely after a couple of extra cycles. For relative dense sands as shown in Figure 3, the shear strain increases approximately in each cycle, rather than just the last few cycles as seen in the relatively loose sands. The median dense sands (Figure 2) presents intermediate behaviors as expected.
The trend of the simulated results for sands from loose to dense state is consistent to the general observations: At the same other conditions, a denser sand have a higher CSR value. As the relative density is increasing, the deformation mode is transferring from liquefaction flow to cyclic mobility. Stress-strain loops for loose sands contain flat segments, a phenomenon term as “neutral phase”, where little or small shear stiffness develops during deformation; stress-strain loops for dense sands have no-zero sloping segments indicating significantly higher shear resistance.
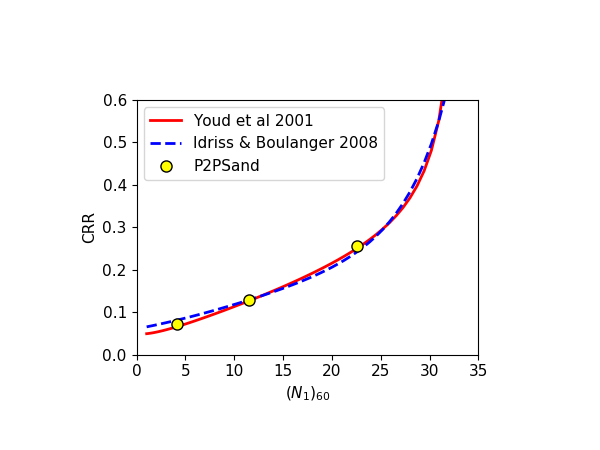
The results by P2PSand model are compared with the empirical curves by Youd et al (2001) and Idriss and Bounlanger (2008) in Figure 4. The relation of \((N_1)_{60} = 46D_r^2\) is used.
Data File
CyclicUndrainedDirectSimpleShear.dat
model large-strain off model configure dynamic fluid model fluid active off zone dynamic active off program call 'input' [input_parameters] ; zone create brick size (1,1,1) ; assign constitutive model zone cmodel assign p2psand ;;; initial conditions zone initialize stress-zz [-Sv0] zone initialize stress-xx [-Sv0*K0] zone initialize stress-yy [-Sv0*K0] ;;; material properties zone property density [rho_d] pressure-ref [Patm] factor-cut 0.01 ;;; input equivalent relative-density-initial corresponding to field condition zone property relative-density-initial [dr0] ;;; or directly input (N1)60 in field condition ;zone property n-1-60 [46.0*dr0*dr0] ;;; initial stresses should be input as properties when p2psand model ;;; is first assigned fish operator ini_stress(z, modelname) if zone.model(z) == modelname then local pp = zone.pp(z) zone.prop(z,'stress-xx-initial') = zone.stress.xx(z) + pp zone.prop(z,'stress-yy-initial') = zone.stress.yy(z) + pp zone.prop(z,'stress-zz-initial') = zone.stress.zz(z) + pp zone.prop(z,'stress-xy-initial') = zone.stress.xy(z) zone.prop(z,'stress-yz-initial') = zone.stress.yz(z) zone.prop(z,'stress-xz-initial') = zone.stress.xz(z) endif end [ini_stress(::zone.list, 'p2psand')] ;;; assign water constitutive model zone fluid cmodel assign isotropic zone fluid property porosity [poro] zone initialize fluid-density [dw] zone gridpoint initialize fluid-modulus 0.0 ;;; boundary conditions zone gridpoint fix velocity-y zone gridpoint fix velocity range position-z 0 zone attach gridpointid 4 to-gridpointid 8 snap off zone attach gridpointid 6 to-gridpointid 8 snap off zone attach gridpointid 7 to-gridpointid 8 snap off ;;; apply conditions zone face apply stress-zz [-Sv0] range position-z 1.0 zone dynamic active on model dynamic time-total 0 zone gridpoint initialize fluid-modulus [Kw] zone gridpoint initialize fluid-tension -1e20 ; [global zptr1 = zone.find(1)] [global gptr1 = gp.near(1,1,1)] fish define ssx local pp1 = zone.pp(zptr1) global sxx = zone.stress.xx(zptr1) + pp1 global syy = zone.stress.yy(zptr1) + pp1 global szz = zone.stress.zz(zptr1) + pp1 global sxz = zone.stress.xz(zptr1) global rup = (p0 + (sxx+syy+szz)/3.0)/p0 global ssx = gp.disp.x(gptr1) end ; zone dynamic damping rayleigh 0.002 1 model dynamic timestep fix 4.0e-5 ; history interval 25 model history dynamic time-total fish history ssx fish history sxz fish history szz fish history rup ; zone gridpoint fix velocity-x [rate] range position-z 1 ; fish define toThisShearStrain if math.abs(ssx) < ssv tothisShearStrain = false else toThisShearStrain = true endif end ; fish define cyclic while_stepping if zone.stress.xz(zptr1) > csr*Sv0 then command zone gridpoint fix velocity-x [-rate] range position-z 1 endcommand else if zone.stress.xz(zptr1) < -csr*Sv0 then command zone gridpoint fix velocity-x [ rate] range position-z 1 endcommand endif end ; model solve dynamic time-total 2000 fish-halt toThisShearStrain history export '1' '2' '3' '4' '5' file [txtfile] truncate model save [savefile]
⇐ Shaking Table Test with Finn Model: Simulation of the Liquefaction of a Layer | Solving Dynamic Problems ⇒
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |