Excavation in a Saturated Soil
Problem Statement
Note
View this project in FLAC3D:
- Pick “ExampleApplications”
- Pick “ExcavationInSaturatedSoil”
- Select “ExcavationIn… .prj” to load
The project’s main data file is shown at the end of this example.
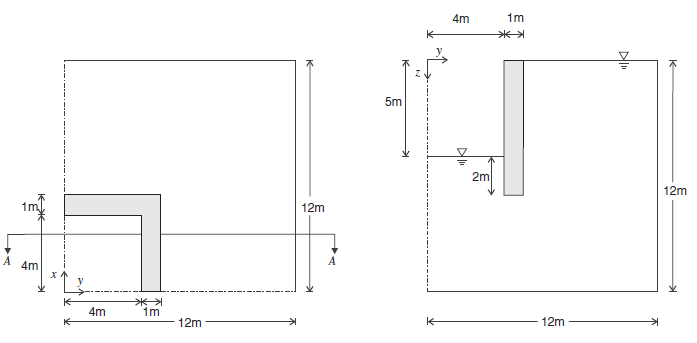
An excavation is planned in a saturated soil layer resting on an impervious base. The soil layer has a thickness of 12 m. The level of the phreatic surface is constant and corresponds to the soil top-surface. The excavation will have a square cross-section of dimensions 8 m × 8 m, and a depth of 5 m. In preparation for this work, the excavation site has been surrounded by vertical impervious walls 1 m thick that extend 2 m below the excavation bottom. After excavation, pumps are installed to lower the water level to the excavation bottom. The problem is to assess the total upheave at the excavation bottom resulting from excavation and drainage.
The problem is three-dimensional but, by symmetry, a quarter of the domain may be considered in the analysis. A system of coordinate axes is defined with the origin at the center of the excavation in the plane of the soil surface, and the \(z\)-axis pointing downward. In this example, boundaries at \(|x|\) = 12 m and \(|y|\) = 12 m are viewed as planes of symmetry. Figure 1 provides a sketch of the problem conditions.
The soil is considered as an elastic material. The soil and water have several properties:
| bulk modulus | \(K\) | 390 MPa |
| shear modulus | \(G\) | 280 MPa |
| soil dry density | \(ρ_d\) | 1200 kg/m3 |
| water density | \(ρ_w\) | 1000 kg/m3 |
| wall density | \(ρ_{wall}\) | 1500 kg/m3 |
| permeability | \(k\) | 10-12 m2/Pa-s |
| porosity | \(n\) | 0.3 |
| fluid bulk modulus | \(K_f\) | 2.0 GPa |
The modulus \(g\) of the gravity vector may be approximated as 10 m/s2. The initial state corresponds to a state of equilibrium (after installation of the walls), in which the horizontal isotropic stresses are such that \(σ'_{xx}\) = \(σ'_{yy}\) = 0.4\(σ'_{zz}\).
Modeling Procedure
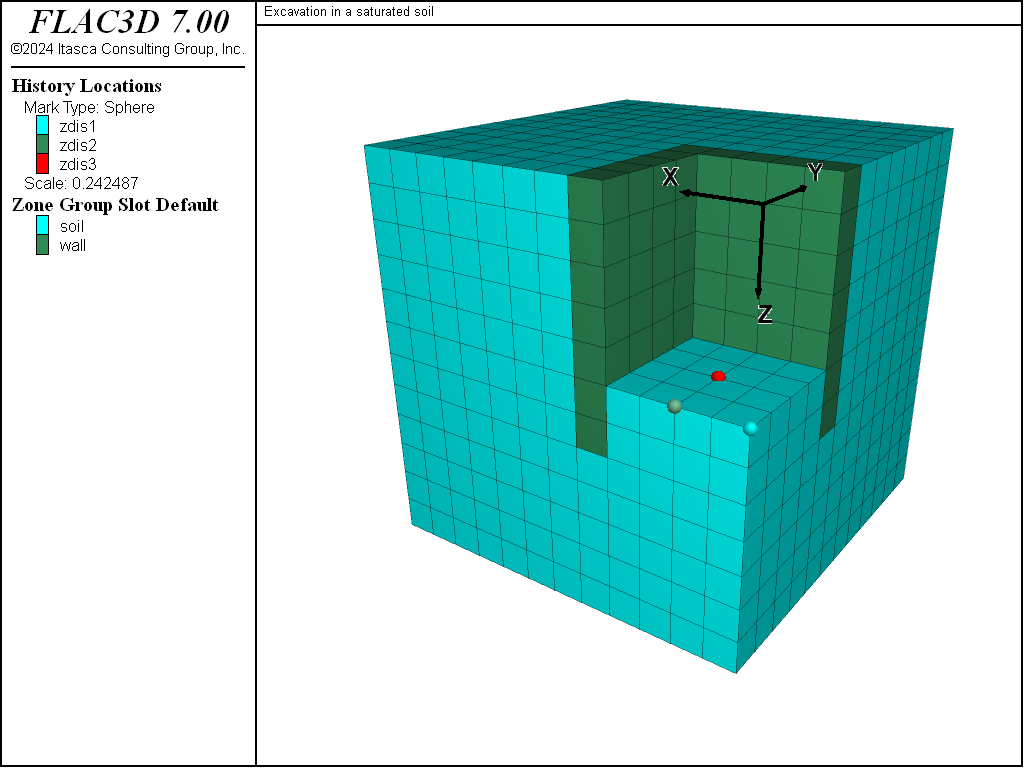
The FLAC3D model has the dimensions 12 m × 12 m × 12 m; the grid has a total of 12 × 12 × 12 cubic zones of the dimensions 1 m × 1 m × 1 m. A fluid null model is assigned to the zones within the excavation and wall volumes, and a mechanical null model is assigned to the zones within the excavation. (See Figure 2 for a plot of the grid with the excavation removed.)
Note that, in this problem, the value \(ρ_d\) + \(n\)\(ρ_w\) for the saturated density of soil is equal to the wall density. Hence, the initial state is characterized by the uniform pore-pressure distribution \(p\) = \(ρ_w\)\(g\)\(z\) and the vertical stress distribution \(σ_{zz}\) = -(\(ρ_d\) + \(n\)\(ρ_w\))\(g\)\(z\). The horizontal stresses are found to be \(σ_{xx}\) = \(σ_{yy}\) = -[0.4\(ρ_d\) + (0.4(n-1)+1)\(ρ_w\)]\(g\)\(z\). Those stresses are applied at the excavation walls to model the initial undisturbed stage.
As an illustration of the modeling procedure for a staged excavation, the analysis is divided into three stages. In the first stage, applied stresses at the excavation walls are changed to the isotropic value \(σ_{xx}\) = \(σ_{yy}\) = \(σ_{zz}\) = - \(ρ_w\)\(g\)\(z\), corresponding to the water pressure in the undrained excavation. The pore pressure is fixed at the excavation bottom and at the soil surface. Flow of water is prevented using the command model fluid active off. The model is cycled to equilibrium to simulate a rapid (undrained) excavation process in the fluid-flow time scale.
In the second stage, the pressures are removed from the excavation walls, and flow of water is again disallowed. The model is cycled to model the effect of rapid lowering of the water table inside the excavation.
In the third stage, the pore pressure is fixed at the value zero at the excavation bottom, flow of water is allowed, and the model is cycled further. The pore pressure is monitored at a point located 1 m below the excavation center (red ball in Figure 2) to detect when steady-state flow conditions are reached. No effort is made to represent the true time scale of consolidation effects; we are simply interested in the final steady state.
The data file for this problem, “excav.dat,” is listed in main data file.
Results
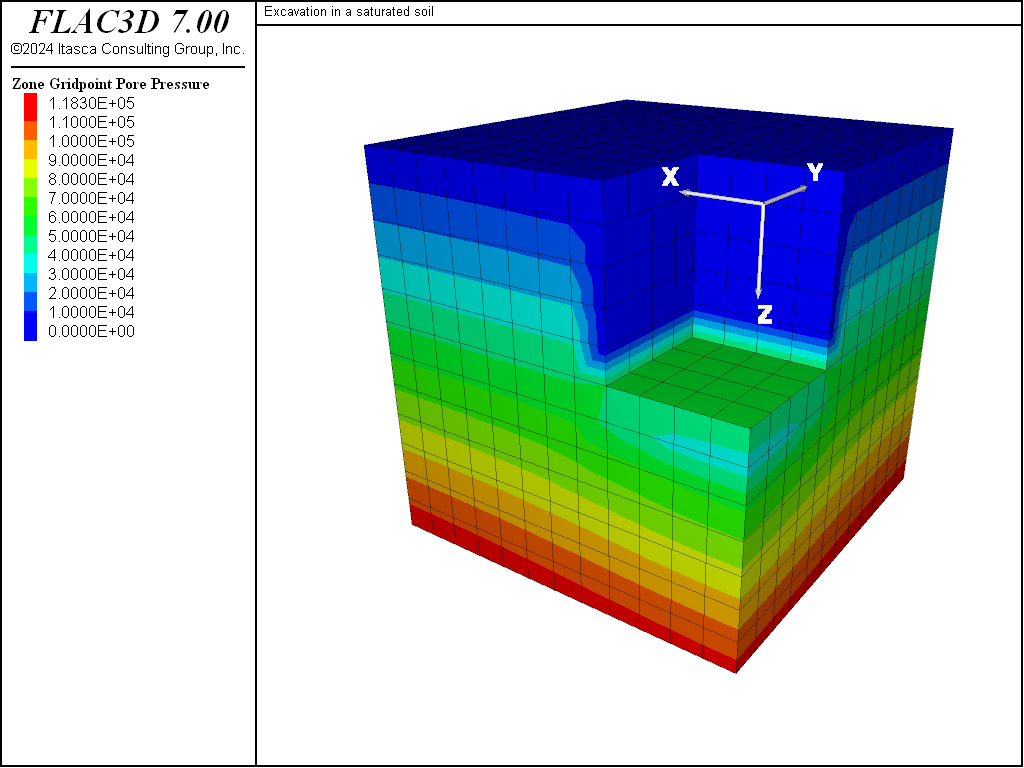
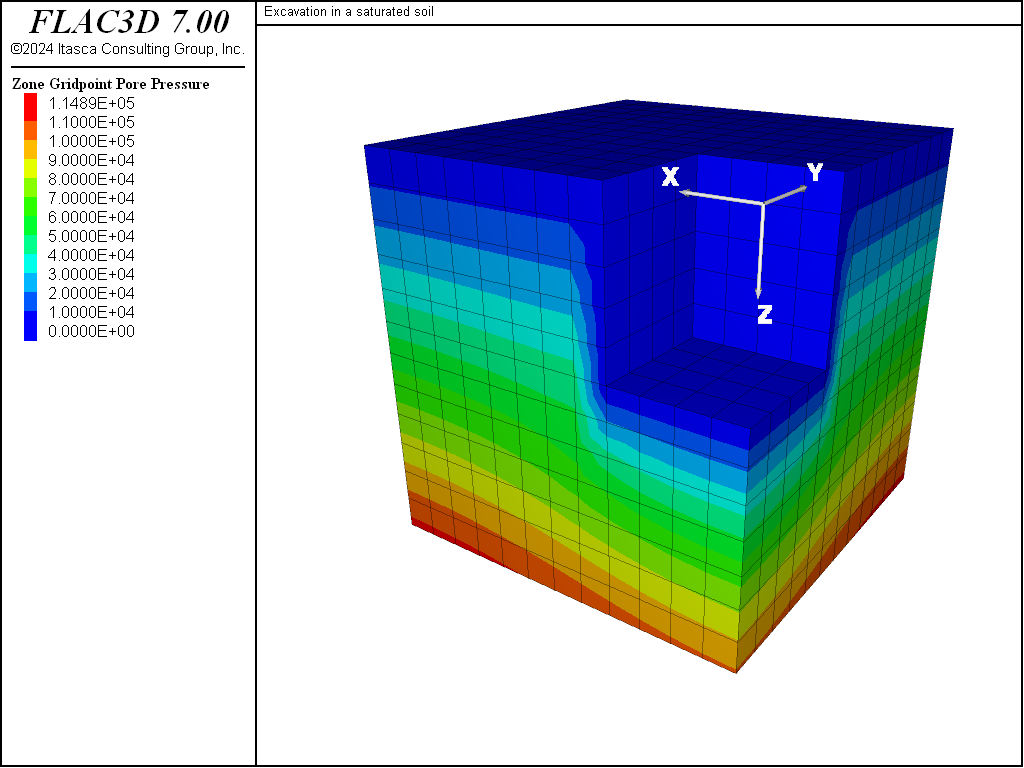
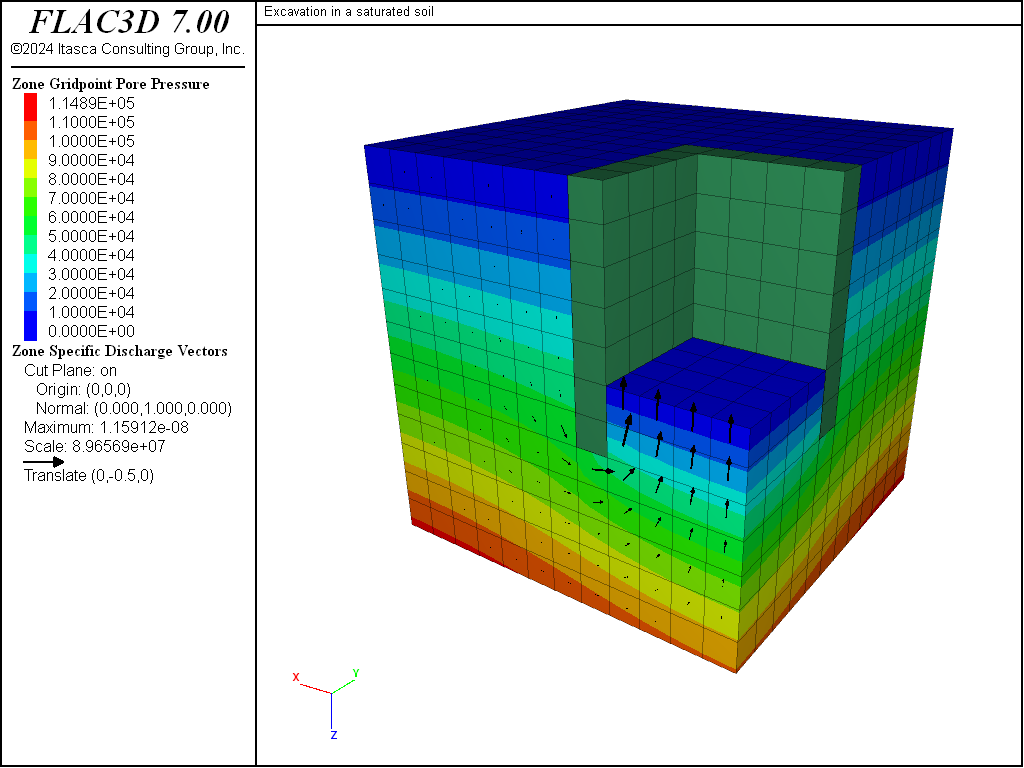
The pore-pressure contours at the end of each of the three stages are shown in Figure 3, Figure 4 and Figure 5.
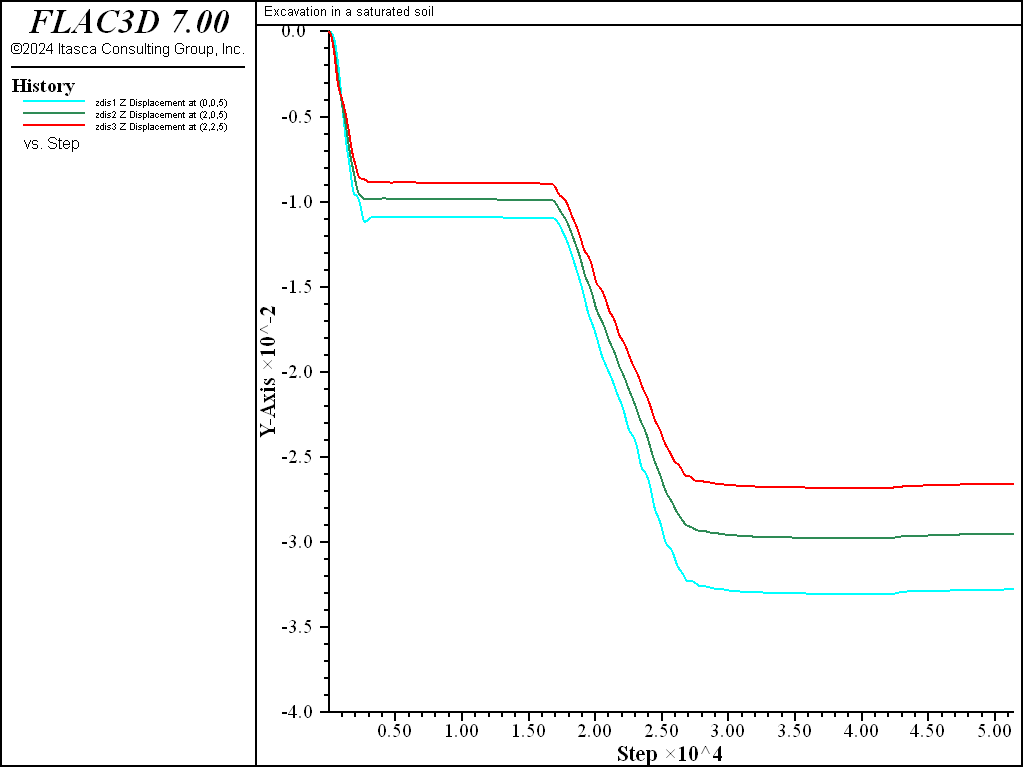
Histories of the vertical displacement at three points at the excavation base (balls in Figure 2) are taken. Results are presented in Figure 6. Heave at the excavation base is shown to occur during the first and second stages. This is caused by the removal of soil and drainage of water inside the excavation. During the third stage, a slight settlement occurs at the base as a result of groundwater flow into the region.
The steady-state flow of groundwater into the excavation at the third stage is shown by the flow vector plot in Figure 7.
Data File
ExcavationInSaturatedSoil.dat
;------------------------------------------------------
; Excavation in a saturated soil
;------------------------------------------------------
model new
model large-strain off
fish automatic-create off
model title 'Excavation in a saturated soil'
model config fluid
; --- geometrical model ---
zone create brick point 1 (12,0,0) point 2 (0,12,0) point 3 (0,0,12) ...
size 12 12 12 rat 1 1 1
zone group 'soil'
zone group 'excavate' range position (0,0,0) (4,4,5)
zone group 'wall' range union position (4,0,0) (5,5,7) ...
position (0,4,0) (4,5,7)
zone face skin ; Label model boundaries
; --- fluid flow model ---
zone fluid cmodel assign isotropic
zone fluid property permeability 1e-12 porosity 0.3
zone initialize fluid-density 1e3
zone gridpoint initialize fluid-modulus 2.0e9
zone gridpoint initialize fluid-tension -1e-3
zone gridpoint initialize pore-pressure 0 gradient (0,0,1e4)
zone fluid cmodel assign null range group 'wall'
; --- mechanical model ---
zone cmodel assign elastic
zone property bulk 3.9e6 shear 2.8e6 density 1.2e3
zone property density 1.5e3 range group 'wall'
; --- initialize stress field to gravity ---
model gravity (0,0,10)
zone initialize-stresses ratio 0.8 total
; --- excavate and label excavation boundaries ---
zone cmodel assign null range group 'excavate'
zone fluid cmodel assign null range group 'excavate'
zone face group 'Base' range position (0,0,5) (4,4,5)
zone face group 'Side' range union position (4,0,0) (4,4,5) ...
position (0,4,0) (4,4,5)
; --- boundary conditions
zone face apply velocity-normal 0 range group 'East' or 'West'
zone face apply velocity-normal 0 range group 'North' or 'South'
zone face apply velocity-normal 0 range group 'Top'
zone gridpoint fix pore-pressure range union group 'Bottom' or 'Base'
zone face apply stress-normal 0 gradient (0,0,-1.2e4) range group 'Side'
zone face apply stress-normal -7.5e4 range group 'Base'
; --- initial state ---
model solve ratio-local 1e-4 ; check initial equilibrium
; --- histories ---
zone history name 'zdis1' displacement-z position (0,0,5)
zone history name 'zdis2' displacement-z position (2,0,5)
zone history name 'zdis3' displacement-z position (2,2,5)
;
; --- excavation ---
model fluid active off
; apply fluid pressure at walls
zone face apply stress-normal 0 gradient (0,0,-1.e4) range group 'Side'
zone face apply stress-normal -5.e4 range group 'Base'
model solve ratio-local 1e-4
model save 'excavation1'
;
; --- drainage ---
zone face apply-remove stress-normal ; remove original static stresses
zone face apply stress-normal 0 gradient (0,0,-1.e4) ...
servo reduce lower-bound 2e-2 ratio local range group 'Side'
zone face apply stress-normal -5.e4 ...
servo reduce lower-bound 2e-2 ratio local range group 'Base'
;
model solve ratio-local 1e-4
model save 'excavation2'
;
; --- percolation ---
model fluid active on
zone gridpoint fix pore-pressure 0 range group 'Base'
model cycle 9000
model save 'excavation3'
⇐ Pillar Loads at Intersecting Tunnels | One-Dimensional Consolidation Considering Secondary Compression ⇒
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |