Factor of Safety Contours
Problem Statement
Note
To view this project in FLAC3D, use the menu command . Choose “TheoryAndBackground/FactorOfSafety/ FOSContours” and select “FOSContours.prj” to load. The project’s main data files are shown at the end of this example.
Typically, application of the strength reduction method produces one single factor of safety per simulation, corresponding to one global minimum stability state. However, the ability to calculate multiple minimum states may be of interest, for example, along a complex slope profile such as a benched cut or a slope with a berm (e.g., see Cheng et al. 2007). A “safety map” may be constructed through a series of analyses using the limit equilibrium method to identify multiple possible failure surfaces for slopes of this type (Baker and Leshchinsky 2001).
A simple procedure to determine multiple local stability states with the strength reduction method is to exclude different regions of the slope when performing the strength reduction calculation.
Alternatively, the explicit dynamic solution method employed in FLAC3D allows multiple local
stability surfaces to be identified in one FLAC3D simulation. When using the
model factor-of-safety command the velocity magnitude of each grid point is stored for each
global factor of safety tested. This data is stored as part of the model state. By comparing the
velocity data at a grid point against a limiting velocity you can determine the greatest factor
of safety checked that resulted in that specific grid point being stable.
By using the bracket-limit keyword you can guarantee that there will be enough tests to fill out a meaningful contour map.
Finding the limiting velocity that determines if a given gridpoint should be considered stable or unstable can be done after the fact, by examining the velocities from the last unstable state and by trying different values in the factor of safety plot until a result seems acceptable.
This technique is demonstrated for a slope profile consisting of two double-inclination slopes separated by a horizontal berm. This example is taken from Cheng et al. (2007), who produced a set of local minimum stability states for this slope using the Morgenstern-Price limit equilibrium method. The slope configuration and resulting local minima locations are shown in Figure 1.
FLAC3D Model
The slope geometry is drawn in the Extrusion pane, and the extruded-grid input record is saved
as data file “geometry.dat”. The slope is oriented in the \(x\)-\(z\) plane and is one
zone thick in the \(y\)-direction. The mesh density is specified with the
extrude set automatic-zone command.
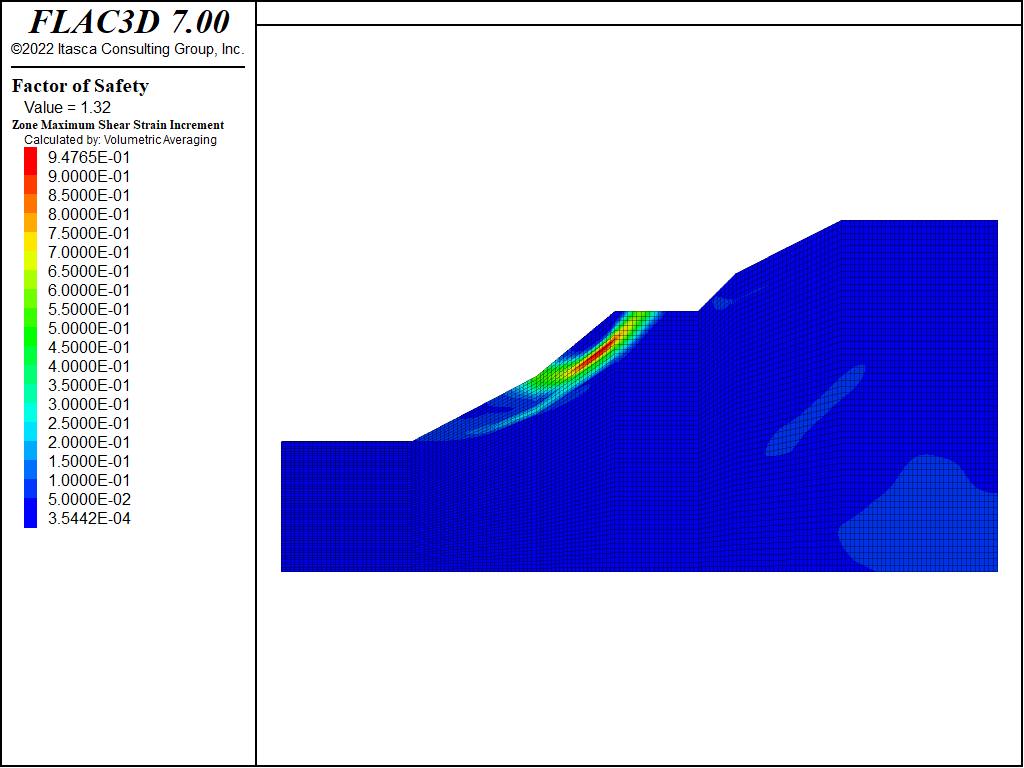
A FLAC3D simulation is first run to determine the global minimum factor of safety for this
slope using the model factor-of-safety command. The result, shown by the shear strain
contour plot in Figure 2, is a global minimum factor of safety of 1.32
with a multiple failure surface that corresponds to the two surfaces with the smallest factor of
safety values shown in the lower slope in Figure 1. The bracket-limit
keyword was used to guarantee a minimum factor of safety test interval of 0.05.
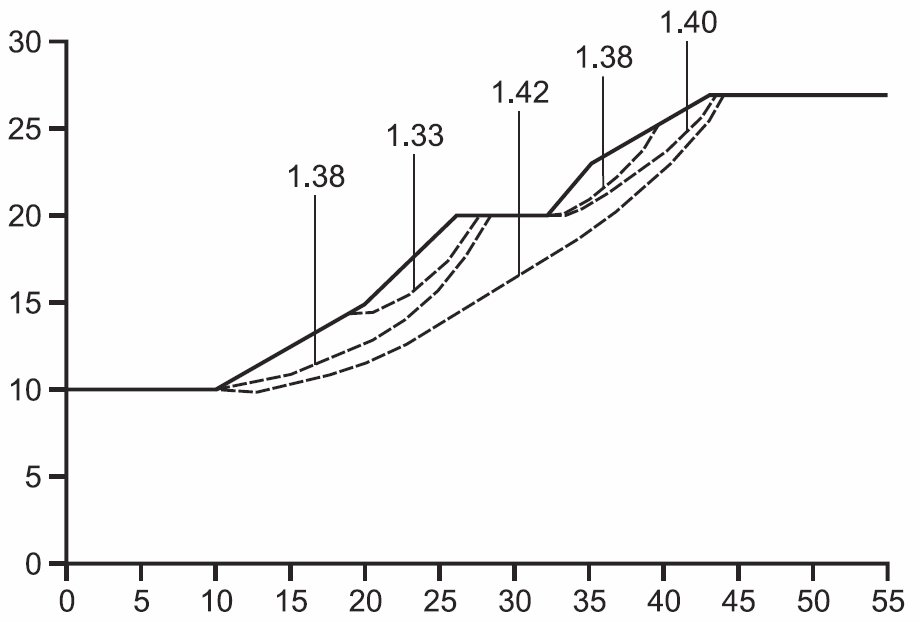
Figure 1: Local minima surfaces from limit equilibrium solution for slope with berm (from Cheng et al. 2007).
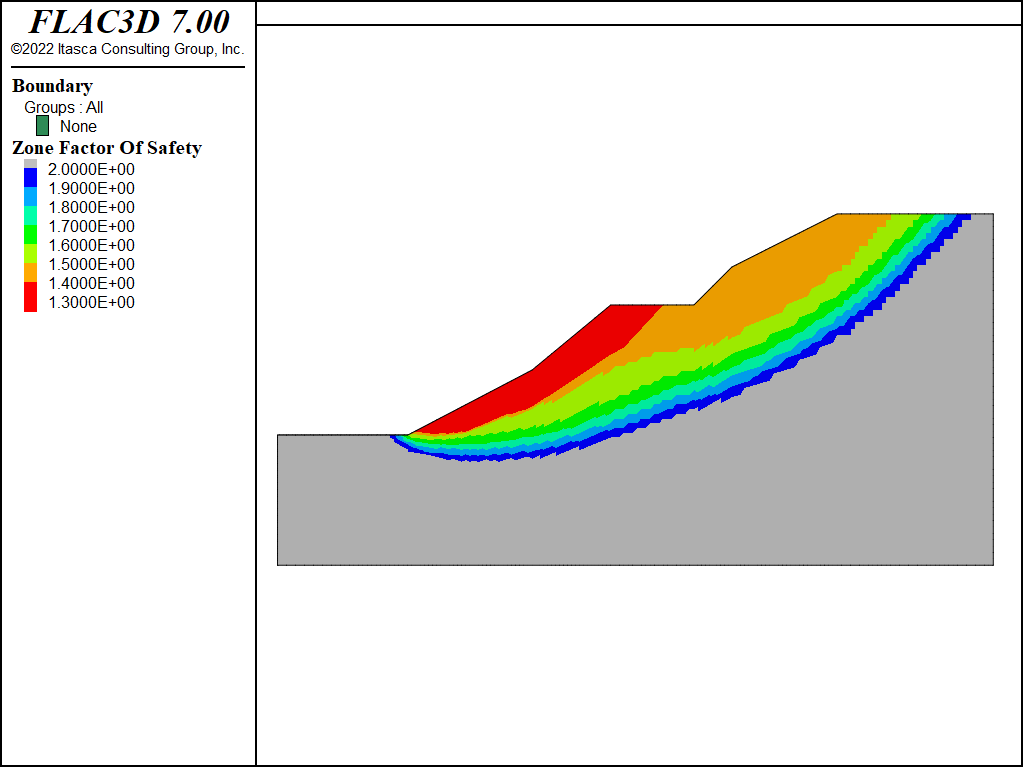
The factor of safety contour plot produced for this example is shown in Figure 3. The contours compare quite well with the local minima surfaces plot in Figure 1. Note that the global minimum contour line (at a factor of 1.33) in Figure 3 closely matches the smallest local minimum surface in Figure 1. The next contour lines, at factors of 1.35 and 1.4 below and above the berm, also compare well with the failure surfaces identified in Figure 3. The factor of safety contour plot also shows a contour shape (see, for example, the 1.45 contour in Figure 3) that curves upward beneath the berm. Note that this effect on the shape of the failure surface is not seen with the limit equilibrium method; compare to the 1.42 surface in Figure 1.
This exercise demonstrates that the strength reduction method can be applied to produce multiple potential failure surfaces in one simulation by monitoring failure in terms of the development of unstable regions (defined by high gridpoint velocities) as the strength of the material is incrementally reduced.
References
Baker, R., and D. Leshchinsky. “Spatial distribution of safety factors,” J. Geotech. Geoenviron. Eng., 127(2), 135-45 (2001).
Cheng, Y.M., T. Lansivaara and W.B. Wei. “Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods,” Computers and Geotechnics, 34, 137-150, 2007.
Data Files
BermFOS.dat
model new
; Geometry created in 2D extruder, exported from state record.
program call 'geometry' suppress
model large-strain off
extrude set automatic-zone direction construction size 160
zone generate from-extrude
zone face skin ; Label model boundaries
; Assign constitutive model and properties
zone cmodel assign mohr-coulomb
zone property bulk 6.25e6 shear 2.88462e6 density 2000
zone property cohesion 5000 friction 30 tension 1e100
; Assign boundary conditions
zone face apply velocity-normal 0 range group 'East' or 'West'
zone face apply velocity-normal 0 range group 'North' or 'South'
zone face apply velocity (0,0,0) range group 'Bottom'
model gravity 10
model solve elastic convergence 1
model save 'initial'
; Solve for initial factor-of-safety
model factor-of-safety convergence 10 filename 'Berm' bracket-limit 0.05
; Save initial state with FOS information included
model save 'final'
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |