Matrix Fluid Flow
Introduction
As well as flow through joints (see Joint Fluid Flow), 3DEC can also model the flow of fluid through the blocks or matrix (between the joints). It is assumed that the blocks represent a saturated, permeable solid, such as soil or cracked rock mass. The flow in the matrix is coupled to the flow in the joints such that fluid in the joints can flow into the surrounding matrix (leak-off). As with the joint flow, the matrix flow modeling may be done by itself, independent of the usual mechanical calculation of 3DEC, or it may be done in parallel with the mechanical modeling in order to capture the effects of fluid/solid interaction.
Several characteristics are provided with the fluid-flow capability.
Different zones may be assigned different permeabilities. Currently only isotropic permeability is possible.
Fluid pressure, flux, and impermeable boundary conditions may be prescribed.
Fluid sources (wells) may be inserted into the material as either point sources or volume sources. These sources correspond to either a prescribed inflow or outflow of fluid and vary with time.
Any of the mechanical and thermal models may be used with the fluid-flow models. In coupled problems, the compressibility and thermal expansion of the saturated material are allowed.
This section is divided into several sub-sections.
The mathematical model description and the corresponding numerical formulation for fluid flow and coupled fluid flow-mechanical processes are described in the 3DEC Fluid-Mechanical Formulation and Numerical Formulation sections.
Properties and Units for Fluid Flow Analysis discusses the material properties required for a fluid-flow analysis, and includes the appropriate units for these properties.
Fluid-Flow Boundary Conditions, Initial Conditions, Sources, and Sinks talks about initial conditions, and provides a description of the different boundary conditions and fluid sources and sinks that can be applied in a 3DEC model.
The calculation modes and associated commands for analyses involving fluid flow are described in Calculation Modes for Fluid-Mechanical Interaction and two verification problems are described in Verification Examples.
Note that a summary of fluid flow properties and units used throughout this section is given in Section 6 ← fix that of this manual, and a summary of 3DEC commands is provided in Section 7. ← and that
3DEC Fluid-Mechanical Formulation – Mathematical Description
In this section, the simulation of fluid flow and fluid-mechanical coupling is considered.
Conventions and Definitions
As a notation convention, the symbol \(a_i\) denotes component \(i\) of the vector \(\{ a \}\) in a Cartesian system of reference axes; \(A_{ij}\) is component \((i,j)\) of tensor \([A]\). Also, \(f_{,i}\) is used to represent the partial derivative of \(f\) with respect to \(x_i\). (The symbol \(f\) denotes either a scalar variable or a vector component.)
The Einstein summation convention applies only on indices \(i\), \(j\), and \(k\), which take the values 1, 2, 3 for components that involve spatial dimensions. The indices may take any values when used in matrix equations.
SI units are used to illustrate parameters and dimensions of variables. See System of Units for conversions to other systems of units.
The following reference quantities are useful in the characterization of transient fluid flow.
Characteristic length:
Fluid diffusivity:
where \(k\) is the mobility coefficient (3DEC permeability), \(M\) is the Biot modulus, \(\alpha\) is the Biot coefficient, \({\alpha}_1 = K + 4/3 G\), \(K\) is the drained bulk modulus, and \(G\) is the shear modulus of the porous material.
The Biot coefficient takes into account the grain compressibility for the porous material. If \(\alpha\) is equal to unity, the grains are considered to be incompressible and the Biot modulus \(M\) is equal to \(K_f / n\), where \(K_f\) is fluid bulk modulus and \(n\) is porosity. The fluid diffusivity becomes
In 3DEC, the Biot coefficient is always 1 (incompressible grains).
Note that for flow-only calculations (rigid material), the fluid diffusivity is
See Properties and Units for Fluid Flow Analysis for additional discussion on the relations between these properties.
Governing Differential Equations
The differential equations describing the fluid-mechanical response of a porous material are as follows.
Transport Law
The fluid transport is described by Darcy’s law:
Where \(q_i\) is the specific discharge vector, \(p\) is fluid pore pressure, \(k\) is the tensor of absolute mobility coefficients (3DEC permeability tensor) of the medium, \(\rho_f\) is the fluid density, and \(g_i\), \(i\) = 1,3 are the three components of the gravity vector.
For future reference, the quantity \(\phi = (p - \rho_f x_j g_j) / (\rho_f g)\) (where \(g\) is the modulus of gravity vector) is defined as the head, and \(\rho_f g \phi\) as the pressure head.
Balance Laws
For small deformations, the fluid mass balance may be expressed as
where \(q_v\) is the volumetric fluid source intensity in [1/sec], and \(\zeta\) is the variation of fluid content or variation of fluid volume per unit volume of porous material due to diffusive fluid mass transport, as introduced by Biot (1956).
The balance of momentum has the form
where \(\rho = \rho_d + n s \rho_w\) is the bulk density, and \(\rho_d\) and \(\rho_w\) are the densities of the dry matrix and the fluid, respectively, \(n\) is porosity, and \(s\) is saturation.
In 3DEC, the saturation is always \(s\) = 1.
Constitutive Laws
Changes in the variation of fluid content are related to changes in pore pressure, \(p\), saturation, \(s\), and mechanical volumetric strains, \(\epsilon\). The response equation for the pore fluid is formulated as
The constitutive response of the porous solid has the form
Where the quantity on the left-hand side is the Terzaghi effective stress, \(H\) is the functional form of the constitutive law, \(K\) is a history parameter, and \(\xi_{ij}\) is the strain rate.
In particular, the elastic relations that relate effective stress to strains are (small strain)
Compatability Equations
The relation between strain rate and velocity gradient is
Numerical Formulation
Introduction
Substitution of the fluid mass balance Equation (6) in the constitutive equation for the pore fluid Equation (8) yields the expression for the fluid continuity equation:
In the 3DEC numerical approach, the flow domain is discretized into tetrahedral zones defined by four nodes. (The same discretization is used for mechanical and thermal calculations, when applicable.) Pore pressure is assumed to be a nodal variable.
The numerical scheme relies on a finite difference nodal formulation of the fluid continuity equation. The formulation can be paralleled to the mechanical constant stress formulation that leads to the nodal form of Newton’s law. It is obtained by substituting the pore pressure, specific discharge vector, and pore-pressure gradient for velocity vector, stress tensor, and strain-rate tensors, respectively. The resulting system of ordinary differential equations is solved using an explicit mode of discretization in time (default mode).
The principal results are summarized below Saturated Fluid Flow. Starting from a state of mechanical equilibrium, a coupled hydromechanical static simulation in 3DEC involves a series of steps. Each step includes one or more flow steps (flow loop) followed by enough mechanical steps (mechanical loop) to maintain quasi-static equilibrium, or an initialization with the block gridpoint initialize pore-pressure, block insitu pore-pressure, or block water table command.
Saturated Fluid Flow
In this section, we consider flow in a medium that remains fully saturated at all times.
Finite-Difference Approximation to Space Derivatives
By convention, the tetrahedron nodes are referred to locally by a number from 1 to 4, face \(n\) is opposite node \(n\), and the superscript (\(f\)) relates to the value of the associated variable on face \(f\).
A linear pore-pressure variation and constant fluid density are assumed within a tetrahedron. The pressure head gradient, expressed in terms of nodal values of the pore pressure by application of the Gauss divergence theorem, may be written as
where \({n}^{(l)}\) is the exterior unit vector normal to face \(l\), \(S\) is the face surface area, and \(V\) is the tetrahedron volume.
For numerical accuracy, the quantity \(x_i - x_i^1\), where \(x_i^1\) corresponds to the coordinates of one of the tetrahedron’s corners, may be substituted for \(x_i\) in the expression of the pressure head in Equation (13) without affecting the value of the pressure head gradient. Accordingly, Equation (13) takes the form
where the nodal quantity \(p^{*l}\) is defined as
Nodal Formulation of the Mass Balance Equation
For fully saturated flow (\(s\) is constant and equal to one), the fluid continuity Equation (12) may be expressed as
where
is the equivalent of the instantaneous “body forces,” \(\rho b_i\), used in the mechanical node formulation, and
First consider a single tetrahedron. Using this analogy, the nodal discharge, \(Q_e^n\) [m3/s], \(n\) = 1,4, equivalent to the tetrahedron-specific discharge and the volumetric source intensity, \(b^*\), may be expressed as
where
and
In principle, the nodal form of the mass balance equation is established by requiring that, at each global node, the sum of equivalent nodal discharges (\(-Q_e^n\)) from tetrahedra meeting at the node and nodal contribution (\(Q_w^n\)) of applied boundary fluxes and sources be zero.
The components of the tetrahedron-specific discharge vector in (19) are related to the pressurehead gradient by means of the transport law (see Equation (50)). In turn, the components of the pressurehead gradient can be expressed in terms of the tetrahedron nodal pore pressures, using Equation (14).
In order to save computer time, local matrices are assembled. A zone formulation is adopted, whereby the sum \(Q_z^n\) of contributions Equation (19) from all tetrahedra meeting at a node, \(n\), is formed. Local zone matrices \([M]\) that relate the four nodal values \(\{ Q_z \}\) to the eight nodal pressure heads \(\{ p^{*} \}\) are assembled. Because these matrices are symmetrical, 10 components are computed; these are saved at the beginning of the computation. By definition of zone matrices, we have
where \(\{ p^* \}\) is the local vector of nodal pressure heads for the zone.
In turn, global nodal values \(Q_T^n\) are obtained by superposition of zone contributions. Taking some liberty with the notation, we write for each global node \(n\),
where \([C]\) is the global matrix and \(\{ p^* \}\) is, in this context, the global vector of nodal pressure heads.
Returning to our previous consideration, we write
where, for simplicity of notation, the \(\sum\) sign is used to represent summation of the contributions at global node \(n\) of all zones meeting at that node. (A zone contribution consists of contributions of tetrahedra involved in the zone.) Using Equation (19) for \(Q_e^n\) and Equation (18) for \(q_v^*\) in Equation (24), we obtain, after some manipulation,
where \(Q_T^n\) is a function of the nodal pore pressures defined in Equation (23) together with Equation (15), \(\sum Q_{app}^n\) is the known contribution of applied volume sources, boundary fluxes, and point sources, having the form
Equation (25) is the nodal form of the mass-balance equation at node \(n\); the right-hand side term \(Q_T^n + \sum Q_{app}^n\) is referred to as the out-of-balance discharge. When the fluid is at rest (the fluid-flow calculation is turned off), the out-of-balance flow discharge vanishes and pore-pressure changes are caused by mechanical and/or thermal deformations only.
In 3DEC, the Biot modulus is a nodal property, and we may write, using Equation (21),
where
After substitution of Equation (27) in Equation (25), we write, rearranging terms,
where
An expression such as Equation (29) holds at each global node involved in the discretization. Together, these expressions form a system of ordinary differential equations that is solved in 3DEC, for given \(d p_v^n / dt\), using the explicit finite-difference scheme.
Explicit Finite-Difference Formulation
In the explicit formulation, the value of the quantity \(p−p_v\) at a node is assumed to vary linearly over a time interval \(\Delta t\). In principle, the derivative in the left-hand side of Equation (29) is expressed using forward finite differences, and the out-of-balance flow-discharge is evaluated at time \(t\). Starting with an initial pore-pressure field, nodal pore pressures at incremental time values are updated, provided the pore pressure is not fixed, using the expression
where
and
Numerical stability of the explicit scheme can only be achieved if the timestep remains below a limiting value.
Stability Criterion
To derive the stability criterion for the flow calculation, we consider the situation in which a node, \(n\), in an assembly of zones is given a pore-pressure perturbation, \(p_0\), from a zero initial state. Using Equation (23), we obtain
After one fluid-flow timestep, the new pore pressure at node \(n\) is (see Equation (31) through Equation (38))
To prevent alternating signs of pore pressures as the computation is repeated for successive \(\Delta t\), the coefficient of \(p_0\) in the preceding relation must be positive. Such a requirement implies that
The value of the poro-mechanical timestep used in 3DEC is the minimum nodal value of the righthand side in Equation (37), multiplied by the safety factor of 0.8.
To assess the influence of the parameters involved, it is useful to keep in mind the following representation of the critical timestep. If \(L_c\) is the smallest tetrahedron characteristic length, we may write an expression of the form
where \(\Delta t_{cr}\) is the critical timestep, \(c\) is the fluid diffusivity, and \(a\) is a constant, larger than unity, that depends on the medium geometrical discretization (e.g., \(a\) = 6 for a regular discretization in cubes; see Karlekar and Desmond (1982) for a thermal analogy).
The critical timestep in Equation (38) corresponds to a measure of the characteristic time needed for the diffusion “front” to propagate throughout the tetrahedron. To estimate the time needed for the front to propagate throughout a particular domain, a similar expression can be used, provided \(L_c\) is interpreted as the characteristic length of the domain under consideration. Consider the case where no leakage occurs and the properties are homogeneous. By taking the ratio of characteristic times for the domain and the tetrahedron, we see that the number of steps needed to model the propagation of the diffusion process throughout that domain is proportional to the ratio of square characteristic lengths for the domain and the tetrahedron. That number may be so large that the use of the explicit method alone could become prohibitive. However, in many groundwater problems, the advantage of this first-order method is that the calculated timestep is usually small enough to follow nodal pore-pressure fluctuations accurately.
Mechanical Timestep and Numerical Stability
The presence of the fluid will increase the apparent mechanical bulk modulus of the medium which, in turn, affects the magnitude of the nodal mass in the density scaling scheme used for numerical stability in 3DEC. An upper bound for this apparent modulus may be found by considering undrained, poro-mechanical conditions for which \({{\partial\zeta}\over{\partial t}}\) = 0. The incremental expression of the fluid constitutive law Equation (8) then takes the form
Adopting the incremental form of the elastic law Equation (10) to describe the volumetric part of the stress-strain constitutive relation in a time interval, we can write
Substitution of Equation (39) in Equation (40) gives
This apparent tangent bulk modulus, \(K + M\), is used in place of \(K\) when calculating nodal inertial mass.
Also note that in 3DEC, the dry density, \({\rho}_d\), of the medium is considered in the input. The saturated density, \(\rho = {\rho}_d + n s{\rho}_f\), is calculated internally using the input value for fluid density, \({\rho}_f\), porosity, \(n\), and saturation, \(s\). Body forces are then adjusted accordingly in Newton’s equations of motion.
Total Stress Correction
In the 3DEC formulation, nodal pore pressures are calculated first. The zone pore pressures are then derived by arithmetic averages of nodal values.
The total stresses are then adjusted, consistent with the definition of Terzaghi effective stress, by adding an increment \(\Delta \sigma_{ij}\) to account for the contribution from pore pressure changes (see Equation (13)). The stress increment \(\Delta \sigma_{ij}\) is expressed as
where
is the contribution from flow, and
is the contribution from the thermal-mechanical coupling. Also, in those expressions, the overline symbol stands for the zone average in the sense mentioned above.
Properties and Units for Fluid Flow Analysis
The properties that relate to fluid flow in 3DEC are the permeability coefficient, \(k\), the fluid mass density, \(\rho_f\) , the fluid bulk modulus, \(K_f\) , and porosity, \(n\). These properties are examined below.
Permeability Coefficient
The isotropic permeability coefficient, \(k\) (e.g., m2/(Pa-sec) in SI units), used in 3DEC is also referred to in the literature as the mobility coefficient. It is the coefficient of the pressure term in Darcy’s law and is related to the hydraulic conductivity, \(k_h\) (e.g., m/s), by the expression
where \(g\) is the gravitational acceleration.
The intrinsic permeability, \(\kappa\) (e.g., in m2), is related to \(k\):
where \(\mu\) is the dynamic viscosity (e.g., units of N-sec/m2).
Equation (45) or Equation (46) may be used to derive \(k\) (required by 3DEC) from either \(k_h\), in velocity units, or \(\kappa\), in [length]2 units (remember that \(k\) must end up with units [L3 T/M] — e.g., in SI units this would be m3 sec/kg (or m2/Pa-sec))). Using the values \(\mu\) = 1.011 × 10-3 kg/(m-sec) for water at 20° C, \(\rho_w g\) = 9.81 × 103 Pa/m and 1 Darcy = 10-8 cm2, conversions may be derived to calculate \(k\) in SI units for water in
\(k\) (in SI units) ≡ \(\kappa\) (in cm2) × 9.9 × 10−2
\(k\) (in SI units) ≡ \(k_h\) (in cm/sec) × 1.02 × 10−6
\(k\) (in SI units) ≡ permeability in darcies × 9.8 × 10−13
If there is a variation of permeability across the grid, the timestep will be controlled by the largest permeability (see Equation (38)). For problems in which steady state (but not transient behavior) is required, it may be beneficial to limit the variations in permeability to improve convergence speed. For example, there will probably be little difference in the final state between systems where there is a 20:1 variation in permeability, compared to a 200:1 variation when the flow is moving entirely from one permeability region to the other.
The isotropic permeability coefficient is a zone property specified using the zone command.
Mass Density
Three different mass densities may be given as input to 3DEC in different circumstances: the dry density of the solid matrix, \(\rho_d\); the saturated density of the solid matrix, \(\rho_s\); and the density of the fluid, \(\rho_f\). Note that densities are only required if gravitational loading is specified.
If 3DEC is configured for fluid flow (model configure matrixflow), then the dry density of the solid material must be used. 3DEC will compute the saturated density of each element using the known density of the fluid and the porosity, \(n\): \(\rho_s = \rho_d + n \rho_f\).
The only case when the saturated density is given as input is for an effective stress calculation (static pore-pressure distribution) not carried out in model configure matrixflow mode. The block water table command, block gridpoint initialize pore-pressure command, or block insitu pore-pressure command specifies the location of the water table. The dry density is specified for zones above the water table, and the saturated density for zones below.
The solid density (dry or saturated) is given using the block zone property density command. The fluid density is imposed globally using the block fluid property density command. All densities are zone variables in 3DEC, and are mass densities (e.g., kg/m3 in SI units).
Fluid Bulk Modulus
The fluid bulk modulus \(K_f\) is defined as
where \(\Delta P\) is the change in pressure for a volumetric strain of \(\Delta V_f / V_f\).
The “compressibility” of the fluid, \(C_f\), is the reciprocal of \(K_f\) (i.e., \(C_f = 1/K_f\)). For example, for pure water at room temperature, \(K_f\) = 2 × 109 Pa, in SI units. In real soils, pore water may contain some dissolved air or air bubbles, which substantially reduce its apparent bulk modulus. For example, Chaney (1978) reports that the fluid modulus can be reduced by an order of magnitude for an air/water mixture at 99% saturation in compacted sand. For groundwater problems, the bulk modulus of water may be different in different parts of the grid to account for the varying amounts of air present. A FISH function may be used to change local moduli according to some law (e.g., the modulus may be made proportional to pressure to represent a gas), but the user should be careful not to make nonphysical assumptions.
Fluid Modulus and Convergence
If a steady-state flow solution is required, the modulus \(K_f\) is unimportant to the numerical convergence process, because the response time of the system and the timestep are both inversely proportional to \(K_f\): the same number of steps are necessary, independent of \(K_f\).
For a transient or coupled analysis, the diffusivity is controlled by the ratio of fluid stiffness to matrix stiffness. The solution will run faster for lower bulk moduli, but the bulk modulus cannot be set to an arbitrarily low value because the time is related to the diffusivity. However, from a numerical point of view, it is not necessary to use values of \(K_f\) that are larger than 20 times (\(K +4/3G)n\) in the simulation (see Storage, Diffusivity, and Timestep).
Fluid modulus is a global variable set using the block fluid property bulk command.
Fluid Modulus for Drained and Undrained Analyses
In 3DEC, whenever the fluid bulk modulus is selected and model configure matrixflow is specified, the drained bulk modulus must be specified for the solid matrix. The apparent (undrained) bulk modulus of the solid matrix will then be computed and will evolve with time.
An undrained analysis may also be performed without specifying model configure matrixflow. In this case, the undrained bulk modulus, \(K_u\), for the solid matrix should be specified. The undrained bulk modulus is
Porosity
Porosity, \(n\), is a dimensionless number defined as the ratio of void volume to total volume of an element. It is related to the void ratio, \(e\), by
The default value of \(n\), if not specified, is 0. \(n\) should be given as a positive number between 0 and 1, but small values (e.g., less than 0.2) should be used with great caution because the apparent stiffness of the pore fluid is proportional to \(K_f /n\). For low values of \(n\), the stiffness may become very large in comparison to the stiffness of the solid material, causing the 3DEC solution to take a very long time to converge. Consider reducing \(K_f\) in this case (see Storage, Diffusivity, and Timestep for further guidance).
Porosity is used by 3DEC to calculate the saturated density of the medium and evaluate Biot modulus in the case when the fluid bulk modulus is given as an input. 3DEC does not update porosity during the calculation cycle, because the process is time-consuming and only the slope of the transient response is affected. Porosity is a zone property specified using the zone command.
Fluid-Flow Boundary Conditions, Initial Conditions, Sources, and Sinks
Boundaries are impermeable by default; all gridpoints/flow knots are initially “free” (i.e., the pore pressure at such knots is free to vary according to the net inflow and outflow from neighboring zones). The opposite condition, bound pp, may also be set at any flow knot. In general, fluid may enter or leave the grid at an external boundary if the pore pressure is fixed.
Pore pressures can be assigned to block boundaries or interior flow knots using the flowknot apply pore-pressure command. The flowknot apply discharge command causes a prescribed inflow or outflow to be applied to the flow knots in the range (volume / time).
Initial distributions of pore-pressure may be specified with the block gridpoint initialize pore-pressure, block water table, or block insitu pore-pressure commands. It is important that the initial distributions are consistent with the gravitational gradient implied by the value of gravity, the given density of water and the values of porosity within the grid. If the initial distributions are inconsistent, then flow may occur in all zones at the start of a run. When setting up a simulation, a few steps should be taken to check for this possibility.
If a model contains joints, effective stresses will be initialized along the joints (i.e., the presence of pore pressures will be accounted for within the contact stresses when stresses are initialized in the grid). This occurs either with or without model configure matrixflow specified. Flow along joints (e.g., fracture flow) is described in “Joint Fluid Flow.”
Calculation Modes for Fluid-Mechanical Interaction
The calculation mode and commands required for a pore-pressure analysis depend on whether the grid has been configured for fluid flow (i.e., whether the model configure matrixflow command has been specified).
The flow calculation can be performed independent of, or coupled to, the mechanical deformation calculation when model configure matrixflow is specified. The different types of coupling that can be performed are described in the sub-section below.
Grid Not Configured for Fluid Flow
If the command model configure matrixflow has not been given, then a fluid-flow analysis cannot be performed, but it is still possible to assign pore pressure at gridpoints and joint contacts. In this calculation mode, pore pressures do not change, but failure, which is controlled by the effective stress state, may be induced when plastic constitutive models are used. In addition, deformation and failure will occur on joints in response to specified pore pressures. This mode is described in more detail in “Pore Pressure in 3DEC”.
Grid Configured for Fluid Flow
If the command model configure matrixflow is given, a transient fluid-flow analysis can be performed, and change in pore pressures can occur. When model configure matrixflow is given, pore pressures are calculated at flow knots rather than gridpoints. Each gridpoint has an equivalent flow knot, except at block boundaries where gridpoints on opposite sides of a joint share a single flow knot. This ensures that the flow in the fracture and in the matrix is coupled. Flow knot pressures are copied to the equivalent gridpoints every step and zone pore pressures are derived using averaging.
Both effective stress (static pore-pressure distribution) and undrained calculations can be carried out in model configure matrixflow mode. In addition, a fully coupled analysis can be performed, in which changes in pore pressure generate deformation, and volumetric strain causes the pore pressure to evolve.
If the grid is configured for fluid flow, dry densities must be assigned by the user (both below and above the water level), because 3DEC takes the fluid influence into account in the calculation of body forces.
Fluid properties are assigned to zones. Zone fluid properties include isotropic permeability and porosity. Zone fluid properties are assigned with the block zone fluid property command. Fluid density and fluid bulk modulus are assigned with the block fluid property command.
The zone fluid properties can be printed with the block zone list fluid command. The flowknot list command can be used to print out flowknot information including volumes and pressures. Fluid density, along with the location of the water table (if specified) can be printed with the block list water command. The fluid flow properties can be plotted –> –> –> ).
An initial gridpoint/flow knot pore-pressure distribution is assigned the same way for the model configure matrixflow mode as for the non-model configure matrixflow mode (i.e., with the block gridpoint initialize pore-pressure command, the block insitu pore-pressure command or the block water table command). Pore pressures can be fixed at boundary gridpoints/flowknots with the flowknot apply pore-pressure command. Fluid sources and sinks can be applied with the flowknot apply discharge or flowplane edge apply discharge commands. Fluid-Flow Boundary Conditions, Initial Conditions, Sources, and Sinks describes the various fluid-flow boundary and initial conditions.
The fluid-flow solution is controlled by the model fluid and model solve commands. Several keywords are available to help the solution process. For example, model fluid active on or off turns on or off the fluid flow calculation mode. The application of these commands and keywords depends on the level of coupling required in the fluid flow analysis as described in the following sub-sections.
Results from a fluid-flow analysis are provided in several forms. The commands block gridpoint list pore-pressure and block zone list pore-pressure print gridpoint and zone pore pressures, respectively. Flow knot information is printed using flowknot list. Histories of flow knot pore pressures can be monitored with the flowknot history pore-pressure command. And for a transient calculation, the pore pressure can be plotted versus real time by monitoring the flow time with the model history fluid time-total command. Plots contours of gridpoint pore pressures (found under –> –> –> ). Specific discharge vectors can be plotted by –> –> –> ). Several fluid-flow variables can be accessed through FISH.
Storage, Diffusivity, and Timestep
The rate of flow through the medium depends on both the permeability and the storativity. The storativity is given by
Where \(K\) is the drained bulk modulus and \(G\) is the shear modulus. The left term represents the fluid storage, whereas the right term depends only on the stiffness of the matrix. The diffusivity is then given by
So, the rate of fluid flow through the medium is proportional to the permeability and inversely proportional to the storage. This means that the rate of flow is therefore proportional to the fluid bulk modulus and matrix modulus. A stiffer fluid will result in faster flow and therefore smaller timesteps.
The fluid timestep depends only on the fluid diffusivity (computed using only the left term of Equation (50) in Equation (51). It also depends on the smallest zone size \(L_z\)
From this, it is clear that a reduction in the fluid bulk modulus will increase the timestep.
In a coupled flow problem, the true diffusivity is controlled by the ratio of fluid stiffness versus matrix stiffness
If \(R_k\) is large (i.e., the fluid stiffness is much greater than the matrix stiffness), the calculated timestep (Equation (52)) will be very small and the problem diffusivity will be controlled by the matrix. The value for \(K_f\) can be reduced in order to increase the timestep and reach steady-state computationally faster. If \(K_f\) is reduced such that \(R_k\) = 20, then the diffusivity should be within 5% of the diffusivity for infinitely stiff fluid. Note that, in any case, \(K_f\) should not be made higher than the physical value of the fluid (2 GPa for water).
Another useful quantity that can be used to help decide on the fluid flow calculation method is the characteristic time of the diffusion process, as given in Equation (54).
The characteristic time of the mechanical process is given in Equation (55).
Flow-Only Calculation
Flow-only calculations may be performed to determine the flow and pressure distribution in some system independent of any mechanical effects. This approach is useful when permeabilities are large or mechanical loading is slow; thereby pore pressures equilibrate quickly and the effect of mechanical loading on the pore pressures can be ignored. In this case, 3DEC may be run in the fluid-flow mode without any mechanical calculation being done. Mechanical calculations may or may not be done subsequently.
The first step in the command procedure for a flow-only calculation is to issue a model configure matrixflow command so that extra memory can be assigned for the fluid-flow calculation. The mechanical calculation should be inhibited with the model mechanical active off command.
The fluid-flow properties must be specified for all zones in which fluid flow may occur. Initial and boundary conditions are assigned to complete the fluid-flow problem setup. Flux boundary conditions, for instance, can be assigned by specifying the flowknot apply discharge command with the range keyword to correspond to the boundaries of that domain. Zones that are excavated are automatically nulled for fluid flow.
The model step command may be specified to execute a given number of fluid-flow steps. Currently there are no model solve capabilities for fluid flow calculations in 3DEC, except for the specification of solution time. Methods for stopping the flow calculation are given in the sub-sections below.
If the computed pore-pressure distribution is then to be used in a mechanical calculation where pore pressure can be assumed to remain constant, the model fluid active off and model mechanical active on commands should be given. The fluid bulk modulus should also be set to zero to prevent extra pore pressures from being generated by mechanical deformation.
Steady State
To solve a flow-only problem to steady state, the time is not important. A reduction in fluid bulk modulus will increase the timestep by Equation (52), but more time will be required to reach equilibrium; therefore, the solution time is not dependent on the choice of \(K_f\). There is currently no model solve command for fluid in 3DEC, so the user must monitor some quantity (e.g., pore pressure) to determine if steady state conditions have been reached (i.e., a negligible change in pore pressures with time). Similarly, the absolute values of permeabilities are not important; however, permeability contrasts are important.
A simple example is given below. A one-dimensional column of height 20 m is created and the pore pressure is held at 1 KPa on the bottom and 0 at the top. The pore pressure evolution at two points is shown in Figure 1 and the final pore pressure with discharge vectors are shown in Figure 2.
Fluid1DFlowCalculation
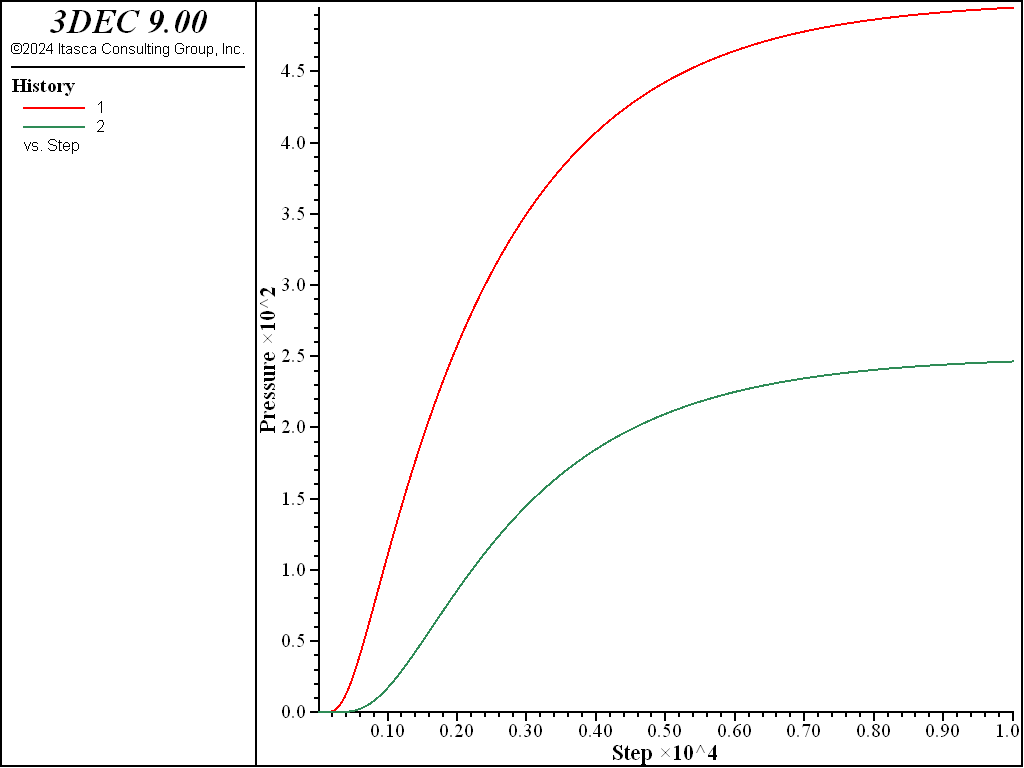
Figure 1: History of pore pressure at two points in the steady-state model.

Figure 2: Pore pressures and discharge vectors in the steady state model after 10,000 steps.
steady_state.dat
model new
model configure matrixflow
model large-strain off
block create brick 0 1 0 1 0 20
block zone generate edgelength 1
block zone cmodel assign elastic
block zone property bulk 5e8 shear 2e8 density 2000
;
block zone fluid property permeability 1e-10 porosity 0.3
block fluid property bulk 2e9
block fluid property density 1000
;
flowknot apply pore-pressure 1e3 range position-z 0
flowknot apply pore-pressure 0 range position-z 20
;
flowknot history pore-pressure position 0 0 10
flowknot history pore-pressure position 0 0 15
;
model fluid active on
model mechanical active off
;
model cycle 10000
;
;
Transient
In situations where time is important, the fluid bulk modulus cannot be set arbitrarily. The rate of flow depends on the storativity Equation (50) but, in a flow-only calculation, there are no mechanical considerations, so the stiffness contribution of the matrix (the right term in Equation (50)) is not calculated. Therefore the user must adjust the fluid bulk modulus to account for this storage term. The apparent fluid bulk modulus is then given by
The steady state example is rerun using this value for the fluid bulk modulus and the pore pressure evolution with time can now be seen (Figure 3). A time for the run can be specified using model solve fluid time. The results look the same as for the steady-state case except that the fluid time is now shown on the \(x\)-axis. A verification of the transient solution using this technique is given in Example “Fluid1DTransientFlow.”
Fluid1DTransientFlow
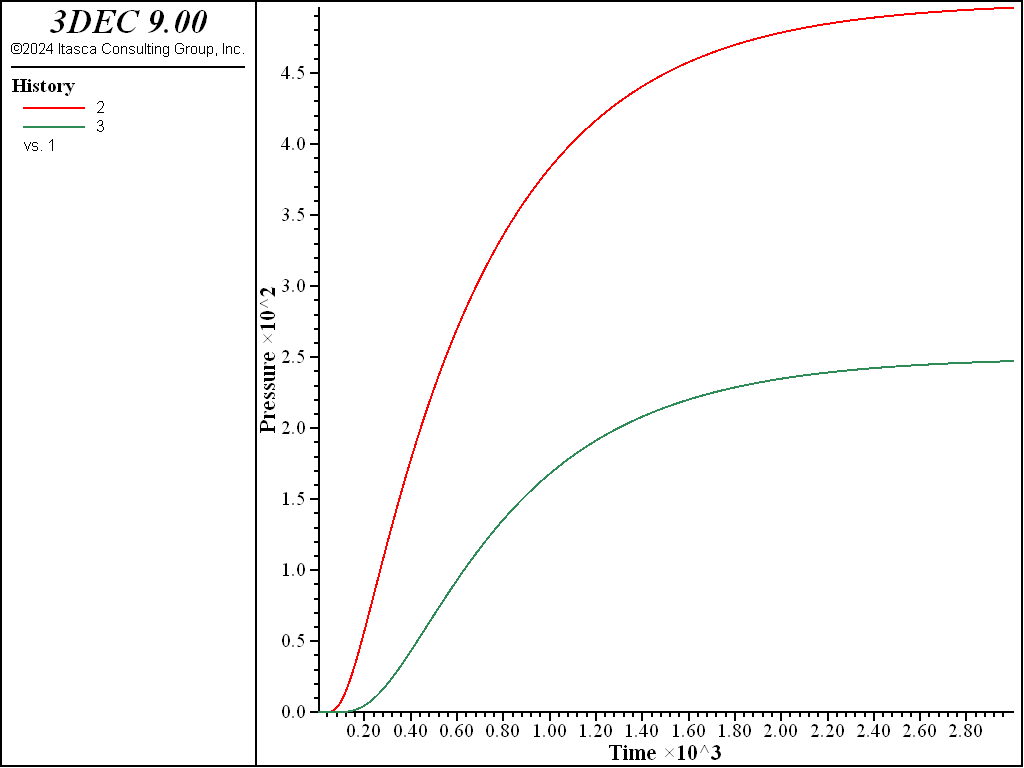
Figure 3: Pore pressure histories for the transient flow example
transient.dat
model new
model configure matrixflow
model large-strain off
;
fish define params
bulk_ = 5e8
shear_ = 2e8
poros_ = 0.3
kf_ = 2e9 ; true bulk modulus of fluid
end
[params]
;
block create brick 0 1 0 1 0 20
block zone generate edgelength 1
block zone cmodel assign elastic
block zone property bulk [bulk_] shear [shear_] density 2000
;
block zone fluid property permeability 1e-10 porosity [poros_]
;
; apparent fluid bulk modulus forigin transient flow
fish define kfa
kfa = poros_/((poros_/kf_)+(1.0/(bulk_+4.0*shear_/3.0)))
end
;
block fluid property bulk [kfa]
block fluid property density 1000
;
flowknot apply pore-pressure 1e3 range position-z 0
flowknot apply pore-pressure 0 range position-z 20
;
model history fluid time-total
flowknot history pore-pressure position 0 0 10
flowknot history pore-pressure position 0 0 15
;
model fluid active on
model mechanical active off
;
model solve fluid time 3000
;
No Flow — Mechanical Generation of Pore Pressure
In situations with very low permeabilities or very fast loading, pore pressure changes will be induced by the mechanical loading faster than they can dissipate. This undrained (short-term) response may be analyzed in 3DEC by configuring the grid for fluid flow (model configure matrixflow) but turning off the fluid flow calculation (model fluid active off). The fluid modulus is given a realistic value and the mechanical calculations are turned on (model mechanical active on). When this is done, pore pressures will be generated as a result of mechanical deformations. For example, the “instantaneous” pore pressures produced by a footing load can be computed in this way.
If the fluid bulk modulus is much greater than the solid bulk modulus, convergence will be slow; it may be possible to reduce the fluid bulk modulus without significantly affecting the behavior (see Storage, Diffusivity, and Timestep).
The data file below illustrates pore pressure buildup produced by a footing load on an elastic-plastic material contained in a box. The left boundary of the box is a line of symmetry, and the pore pressure is fixed at zero along the top surface to prevent pore-pressure generation there. The porosity is set to 0.5; the permeability is not needed because flow is not calculated.
undrained.dat
model new
model random 10000
model configure matrixflow
model large-strain off
block create brick 0 21 0 1 0 10
block densify segments 7 1 4 join
block zone generate edgelength 0.5 range position-x 0 6 position-z 4 10
block zone generate edgelength 1
;
; --- mechanical model ---
block zone cmodel assign mohr-coulomb
block zone property density 2000 bulk 5e7 shear 3e7 ...
friction 25 cohesion 1e5 tension 1e10
block gridpoint apply velocity-x 0 range position-x 0
block gridpoint apply velocity-z 0 range position-z 0
block gridpoint apply velocity-x 0 range position-x 21
block gridpoint apply velocity-y 0 range position-y 0
block gridpoint apply velocity-y 0 range position-y 1
;
; --- apply load slowly ---
fish define ramp
ramp = math.min(1.0,float(global.step)/1000.0)
end
block face apply stress-zz -0.3e6 fish ramp ...
range position-x -0.1 3.1 position-z 10
; --- fluid flow model ---
block zone fluid property porosity 0.5
block fluid property bulk 9e8
;
; --- fix pp to 0 at surface
flowknot apply pore-pressure 0 range position-z 10
;
; --- histories ---
flowknot history pore-pressure position 2 0.5 9
;
; --- solve undrained ---
model fluid active off
model mechanical active on
block zone nodal-mixed-discretization on
model solve
model save 'load'
As a large amount of plastic flow occurs during loading, the normal stress is applied gradually by using the FISH function ramp to supply a linearly varying multiplier to the bound command. Figure 4 shows pore-pressure contours and displacement vectors. It is important to realize that the plastic flow will occur in reality over a very short period of time (of the order of seconds); the word “flow” here is misleading because, compared to fluid flow, it occurs instantaneously. Hence, the undrained analysis (with model fluid active off) is realistic.
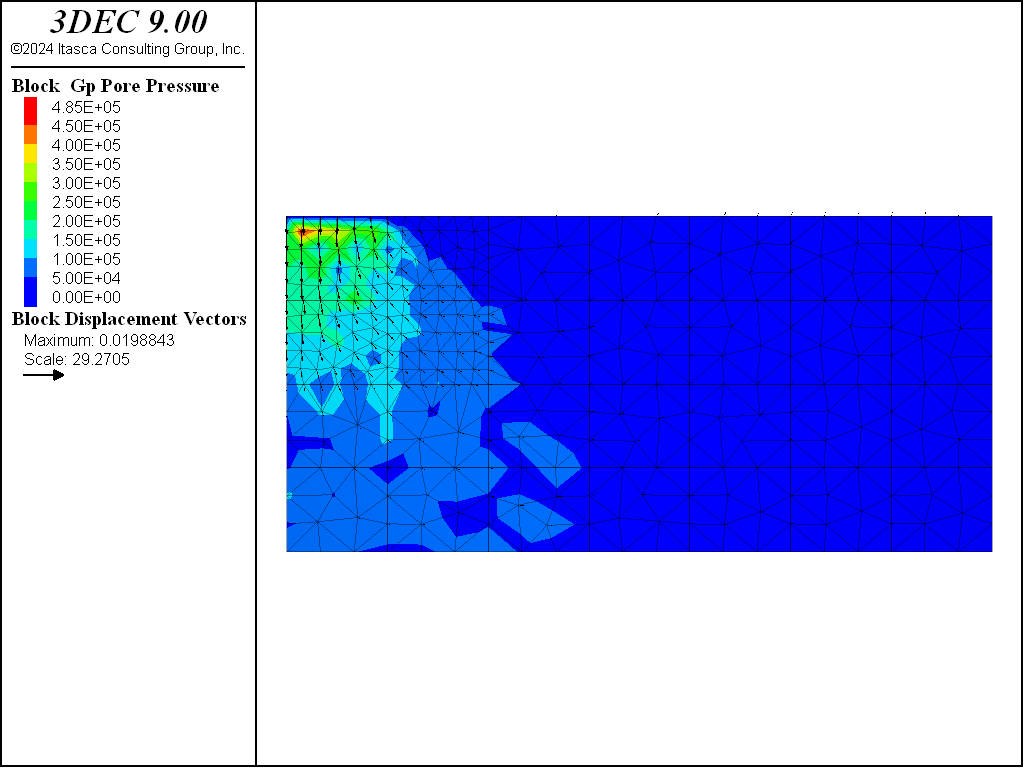
Figure 4: Pore pressures and displacements in undrained model.
Unfortunately, linear tetrahedral elements (as used in 3DEC) are not very good at simulating undrained conditions. This is evident from the uneven pore pressure contours in Figure 4. Currently, the fluid flow logic does not work with hexahedral zones or higher order tetrahedral zones in 3DEC. One way to overcome this problem is to perform the undrained simulation without model configure matrixflow on. To use this “dry” method, set the solid bulk modulus to the undrained value:
Then set the pore pressures using block insitu pore-pressure or block water table. Note that this approach assumes perturbations in pore pressure due to mechanical effects are small relative to the in-situ pore pressures.
Coupled Flow and Mechanical Calculations
By default, 3DEC will do a coupled fluid-flow and mechanical calculation if the grid is configured for fluid, and if the fluid bulk modulus and permeability are set to realistic values. The full fluid-mechanical coupling in 3DEC occurs in two directions: pore-pressure changes cause volumetric strains that influence the stresses; in turn, the pore pressure is affected by the straining that takes place.
The relative time scales associated with consolidation and mechanical loading should be appreciated. Mechanical effects occur almost instantaneously (of the order of seconds, or fractions of seconds). However, fluid flow is a long process: the dissipation associated with consolidation takes place over hours, days or weeks.
Relative time scales may be estimated by considering the ratios of characteristic times for the coupled and undrained processes. The characteristic time associated with the undrained mechanical process is found by using the saturated mass density for \(\rho\) and the undrained bulk modulus, \(K_u\), as defined in Equation (48) for \(K\) in Equation (54). The ratio of the diffusion characteristic time (Equations (54) and (55)) and the undrained mechanical characteristic time is thus
In most cases, \(M\) is approximately 1010 Pa, but the mobility coefficient \(k\) may differ by several orders of magnitude; typical values are
10−19m2/Pa-sec for granite;
10−17m2/Pa-sec for limestone;
10−15m2/Pa-sec for sandstone;
10−13m2/Pa-sec for clay; and
10−7m2/Pa-sec for sand.
For rock and soil, \(\rho\) is of the order of 103 kg/m3, while \(K +4/3G\) is approximately 1010 Pa. Using those orders of magnitude in Equation (58), we see that the ratio of fluid-to-mechanical time scales may vary between \(L_c\) for sand, \(10^6\ L_c\) for clay, \(10^8\ L_c\) for sandstone, \(10^{10}\ L_c\) for limestone, and \(10^{12}\ L_c\) for granite. If we exclude materials with mobility coefficients larger than that of clay, we see that this ratio remains very large, even for small values of \(L_c\).
In practice, mechanical effects can then be assumed to occur instantaneously when compared to diffusion effects. This is also the approach adopted in 3DEC, where no time is associated with any of the mechanical steps taken together with the fluid-flow steps. The use of the dynamic option in 3DEC may be considered to study the fluid-mechanical interaction in materials such as sand, where mechanical and fluid time scales are comparable.
In most modeling situations, the initial mechanical conditions correspond to a state of equilibrium that must first be achieved before the coupled analysis is started. Typically, at small fluid-flow time (compared to \(t_c\) — see Equation (54)), a certain number of mechanical steps must be taken for each fluid step to reach quasi-static equilibrium. At larger fluid-flowtime, if the system approaches steady-state flow, several fluid-flow timesteps may be taken without significantly disturbing the mechanical state of the medium. A corresponding numerical simulation may be controlled manually by alternating between flow-only (model fluid active on and model mechanical active off) and mechanical-only (model fluid active off and model mechanical active on) modes. The model step command can be used to perform calculations for both the flow-only and mechanical-only processes.
As an alternative approach, the tedious task of switching between flow-only and mechanical-only modes may be avoided by using the model solve or model cycle command in combination with appropriate settings. By default, if both flow and mechanical calculations are on, 3DEC takes one mechanical timestep for each fluid timestep. Generally, it is desirable to reach a quasi-equilibrium state for each mechanical calculation, so more mechanical steps are probably wanted for each fluid step. This is achieved by using the command model mechanical substep n with model mechanical follower on. If \(n\) = 100, then 100 mechanical steps will be executed for each fluid step.
It is also possible to set a limit to the out-of-balance force under which quasi-static mechanical equilibrium is assumed using the mechanical ratio keywords with the model solve command. Mechanical stepping will stop when the unbalanced force falls below the specified limit and the next fluid step will be executed.
In some circumstances, the user may wish to execute multiple fluid steps per mechanical step. This can be achieved by using the model fluid follower on and model fluid substep commands.
Fully Coupled Analysis
To illustrate a fully coupled analysis, we continue the footing simulation done in the No Flow — Mechanical Generation of Pore Pressure section with appropriate settings to calculate the consolidation beneath the footing. Note that when the command model solve fluid time is given, a ratio is also provided. This is because as the calculation progresses, the mechanical unbalanced force ratio decreases below the default threshold for solution (1.0e-5); therefore, to ensure that the desired amount of fluid time is simulated, the ratio threshold must be decreased.
The data file is “COUPLED.3DDAT” shown below.
coupled.3ddat (matrix)
model restore 'load'
;
; --- turn on fluid flow ---
block zone fluid property permeability 1e-12
block gridpoint initialize displacement 0 0 0
block gridpoint initialize velocity 0 0 0
block initialize velocity 0 0 0
;
; --- histories ---
history delete
history interval 1000
model history fluid time
block history displacement-z position 0 1 10
block history displacement-z position 1 1 10
block history displacement-z position 2 1 10
flowknot history pore-pressure position 2 1 9
flowknot history pore-pressure position 5 1 5
flowknot history pore-pressure position 10 1 7
;
; --- set mechanical limits ---
model fluid active on
model mechanical substep 100
model mechanical follower on
;
; --- solve to 1 million seconds ---
;
model mechanical time-total 0
model solve fluid time 1e6 or ratio 1e-4
model save 'age_1e6'
;
The screen printout should be watched during the calculation process — eight variables are updated on the screen after the model solve command is issued: 1) the current step number; 2) the time; 3) the maximum (mechanical) unbalanced force; 4) the clock time; 5) the unbalanced force ratio (mechanical); 6) the flow time; 7) the number of mechanical steps executed this flow step; and 8) the number of fluid steps executed this mechanical step.
The unbalanced force-ratio limit is set to 1e-4 for this problem; enough mechanical steps are taken to keep the maximum unbalanced force ratio below this limit. However, the limit to mechanical steps, defined by model mechanical substep is set to 100 in this example. If the actual number of mechanical steps taken is always equal to the set value of model mechanical substep, then something must be wrong. Either the force limit or number of substeps has been set too low, or the system is unstable and cannot reach equilibrium. The quality of the solution depends on the force tolerance: a small tolerance will give a smooth, accurate response, but the run will be slow; a large tolerance will give a quick answer, but it will be noisy.
Figure 5 shows the time histories to 1,000,000 seconds of displacements under the footing load (approximately 11.5 days). In this simulation, pore pressures remain fixed at zero on the ground surface; hence, the excess fluid escapes upward. The leveling off of the histories indicates that full consolidation has been reached.
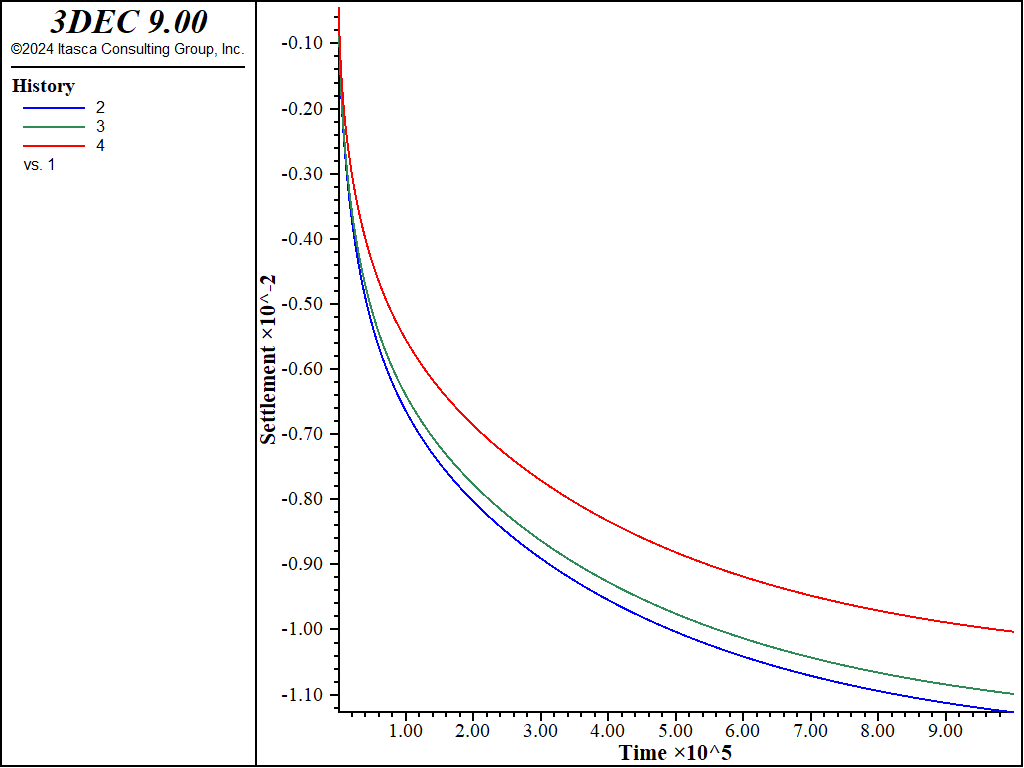
Figure 5: Histories of displacement under the footing for the coupled analysis.
Uncoupled Analysis
The fully coupled simulation takes quite a long time to run. In many circumstances, fairly accurate results can be obtained with an uncoupled approach. This example shows how this could be done for the footing problem.
First, a flow-only calculation is made with fluid bulk modulus set using Equation (56), then a mechanicalonly calculation is performed with fluid bulk modulus set to zero. The final displacements for the uncoupled drained simulation are plotted in Figure 6. The final settlement matches within 3% of the coupled flow results.
uncoupled.3ddat
model restore 'load'
;
; --- turn on fluid flow ---
block zone fluid property permeability 1e-12
block gridpoint initialize displacement 0 0 0
block gridpoint initialize velocity 0 0 0
block initialize velocity 0 0 0
;
; --- histories ---
history delete
history interval 100
model history fluid time
block history displacement-z position 0 1 10
block history displacement-z position 1 1 10
block history displacement-z position 2 1 10
flowknot history pore-pressure position 2 1 9
flowknot history pore-pressure position 5 1 5
flowknot history pore-pressure position 10 1 7
;
; solve uncoupled to 1 million sec ---
;
model fluid active on
model mechanical active off
model mechanical time-total 0
;
fish define kfa
kfa = 0.5/((0.5/9e8)+(1.0/(5e7+4.0*3e7/3.0)))
end
;
block fluid property bulk [kfa]
model solve fluid time 1e6
;
;
model fluid active off
model mechanical active on
block fluid property bulk 0
model solve
;
;
model save 'age_1e6_uncoup'
;
;

Figure 6: Displacement under the footing for the uncoupled analysis.
Selection of a Modeling Approach for Fully Coupled Analysis
As shown above, a fully coupled hydromechanical analysis with 3DEC is often time consuming and sometimes unnecessary. The following guidelines suggest when to use each modeling approach.
Long-Term Behavior (Drained Response)
If the time of interest is much greater than the characteristic diffusion time, \(t_c\) Equation (54), then the pore-pressure field can be uncoupled from the mechanical field. Steady state pore pressure can be determined with a fluid-only simulation (Flow-Only Calculation) or by specifying pore pressures and not doing any flow calculations at all (Pore Pressure and Effective Stress).
Short-Term Behavior (Undrained Response)
If the time of interest is very short compared to the characteristic diffusion time, \(t_c\) Equation (54), then the influence of fluid flow on the simulation results will probably be negligible. An undrained simulation can be performed as described in the No Flow — Mechanical Generation of Pore Pressure section.
Medium-Term Behavior (Coupled Response) — Stiff Matrix
If the time of interest is of the order of \(t_c\), and the matrix is stiff relative to the fluid (\(R_k\) << 1 in Equation (53)), then the fully coupled simulation is not required. The modeling technique will depend on the driving mechanisms (fluid or mechanical perturbation):
In mechanically driven simulations, the pore pressure may be assumed to remain constant. A no-flow approach may be used (Pore Pressure and Effective Stress).
In pore pressure-driven simulations (e.g., settlement caused by fluid extraction), volumetric strains will not significantly affect the pore-pressure field, and the flowcalculation can be performed independently. Perform a fluid-only flow calculation (Flow-Only Calculation) followed by a mechanical only calculation with the fluid bulk modulus set to 0 (Uncoupled Analysis).
Medium-Term Behavior (Coupled Response) — Soft Matrix
If the time of interest is of the order of \(t_c\), and the matrix is soft relative to the fluid (\(R_k\) > 1 in Equation (53)), then the modeling approach depends on the driving mechanism.
In mechanically driven simulations, calculations can be time consuming. As discussed in Storage, Diffusivity, and Timestep, it may be possible to reduce the value of \(K_f\), such that \(R_k\) = 20, and not significantly affect the response.
In most practical cases of pore pressure-driven systems, experience shows that the coupling between pore pressure and mechanical fields is weak. It may be possible to perform the simulation in flow-only mode followed by mechanical-only mode. See Uncoupled Analysis.
Verification Examples
Several verification problems that illustrate the fluid-flow modeling capabilities in 3DEC are presented.
Transient Groundwater Flow in a Confined Layer
A long embankment of width \(L\) = 100 m rests on a shallow saturated layer of soil. The width (\(L\)) of the embankment is large in comparison to the layer thickness, and its permeability is negligible when compared to the permeability, \(k\) = 10-12 m2/(Pa sec), of the soil. The Biot modulus for the soil is measured to be \(M\) = 10 GPa. Initial steady-state conditions are reached in the homogeneous layer. The purpose is to study the pore-pressure change in the layer as the water level is raised instantaneously upstream by an amount \(H_0\) = 2 m. This corresponds to a pore-pressure rise of \(p_1 = H_0 {\rho}_w g\) (with the water density \({\rho}_w\) = 1000 kg/m3 and acceleration of gravity \(g\) = 10 m/s2) at the upstream side of the embankment. Figure 7 shows the geometry of the problem.
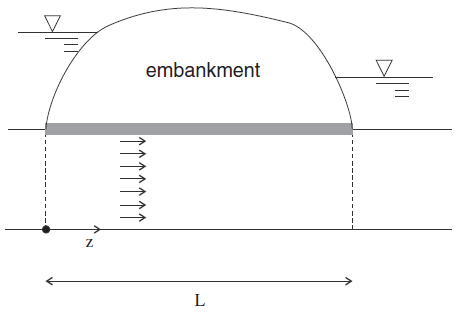
Figure 7: Confined flow in a soil layer.
The flow in the layer may be assumed to be one-dimensional. The model has width \(L\). The excess pore pressure, \(p\), initially zero, is raised suddenly to the value \(p_1\) at one end of the model. The corresponding analytical solution has the form
where the \(z\)-axis is running along the embankment width and has its origin at the upstream side, \(\hat{p} = {p\over p_1}\), \(\hat{z} = {z \over {L}}\), \(\hat{t} = c t/L^2\) and \(c = M k\).
In the 3DEC model, the layer is defined as a column of 25 joined blocks. The excess pore pressure is fixed at the value of 2 ×104 Pa at the face located at \(z\) = 0, and at zero at the face located at \(z\) = 100 m. The model grid is shown in Figure 8.
The analytical solution is programmed as a FISH function for direct comparison to the numerical results at selected fluid-flow times corresponding to \(\hat{t}\) = 0.05, 0.1, 0.2 and 1.0. The analytical and numerical pore-pressure results for these times are stored in tables.
Figure 8: 3DEC grid for fluid flow in a confined soil layer.
Example “verification-transient.dat” contains the 3DEC data file for this problem, using the explicit formulation to obtain the solution. The corresponding project file, “verification-transient.3dprj”, is located in the “datafiles\Fluid-flow\matrix flow” folder. The comparison of analytical and numerical excess pore pressures at four fluid-flow times for the explicit solution is shown in Figure 9. Normalized excess pore pressure (\(p/p_1\)) is plotted versus normalized distance (\(z/L\)), where Tables 2, 4, and 6 contain the analytical solution for excess pore pressures, and Tables 1, 3, and 5 contain the 3DEC solutions. The four flow times are 5 × 104, 105, 2 × 105, and 106 seconds for the explicit and implicit solutions. Steady-state conditions are reached by the last time considered. For both solution formulations, the difference between analytical and numerical pore pressures at steady state is less than 0.1%.
verification-transient.dat
program log on
program log-file 'verification-transient.log'
; -------------------------------------------------------------------------
;
; --- confined 1d transient flow ---
;
; -------------------------------------------------------------------------
model new
fish automatic-create off
;
model title 'Unsteady groundwater flow in a confined layer: explicit method'
;
model configure matrixflow
model large-strain off
;
; --- fish constants ---
fish define constants
global c_cond = 1e-12 ; permeability
global c_biom = 1e10 ; biot modulus
global length = 100. ; layer width
global dp1 = 2e4 ; pore pressure rise, face 1
global tabn = -1
global tabe = 0
global overl = 1. / length
local d = c_cond * (c_biom)
global dol2 = d * overl * overl
global pi2 = math.pi * math.pi
end
[constants]
;
block create brick 0 10 0 10 0 [length]
;
block zone generate edgelength 10
;
block zone cmodel assign elastic
block zone property density 2500 shear 2e9 bulk 5e9
;
block zone fluid property permeability [c_cond]
; Biot modulus = Kf/n. Let porosity = 0.5, therefore Kf = 0.5e10
block zone fluid property porosity 0.5
block fluid property bulk 0.5e10
block fluid property density 1000
;
flowknot apply pore-pressure [dp1] range position-z 0
flowknot apply pore-pressure 0 range position-z 100
;
model history fluid time
flowknot history pore-pressure position 0 0 0
flowknot history pore-pressure position 0 0 50
flowknot history pore-pressure position 0 0 100
;
; --- fish function ---
fish define num_sol
tabn = tabn + 2
local t_hat = fluid.time.total * dol2
loop foreach local pnt block.gp.list
local rad = math.sqrt(block.gp.pos.x(pnt)^2 + ...
block.gp.pos.y(pnt)^2) * overl
if rad < 1.e-4 then
local x = block.gp.pos.z(pnt) * overl
table(tabn,x) = block.gp.pp(pnt) / dp1
end_if
end_loop
table.label(tabn) = '3DEC at '+string(t_hat)
end
;
fish define ana_sol
local top = 2. / math.pi
local n_max = 100 ; max number of terms -exact solution
tabe = tabe + 2
local t_hat = fluid.time.total * dol2
local tp2 = t_hat * pi2
loop foreach local pnt block.gp.list
local rad = math.sqrt(block.gp.pos.x(pnt)^2 + ...
block.gp.pos.y(pnt)^2) * overl
if rad < 1.e-4 then
local x = block.gp.pos.z(pnt) * overl
local n = 0
local nit = 0
local tsum = 0.0
local tsumo = 0.0
local converge = 0
loop while n < n_max
n = n + 1
local fn = float(n)
local term = math.sin(math.pi*x*fn) * math.exp(-tp2*fn*fn) / fn
tsum = tsumo + term
if tsum = tsumo then
nit = n
table(tabe,x) = 1. - x - top * tsum
converge = 1
n = n_max
else
tsumo = tsum
end_if
end_loop
if converge = 0 then
local str = ...
string.build("no convergence x = %1 - t = %2",x,fluid.time.total)
local oo = io.out(str)
exit
end_if
end_if
end_loop
table.label(tabe) = 'Analytical at '+string(t_hat)
end
;
; --- settings ---
model mechanical active off
model fluid active on
;
; --- test ---
model solve fluid time 5e4
block gridpoint list pore-pressure ...
range position-x -0.001 0.001 position-y -0.001 0.001
[num_sol]
[ana_sol]
;
model solve fluid time 10e4
[num_sol]
[ana_sol]
;
model solve fluid time 20e4
[num_sol]
[ana_sol]
;
model solve fluid time 100e4
[num_sol]
[ana_sol]
;
model save 'verification-transient'
;
;
;
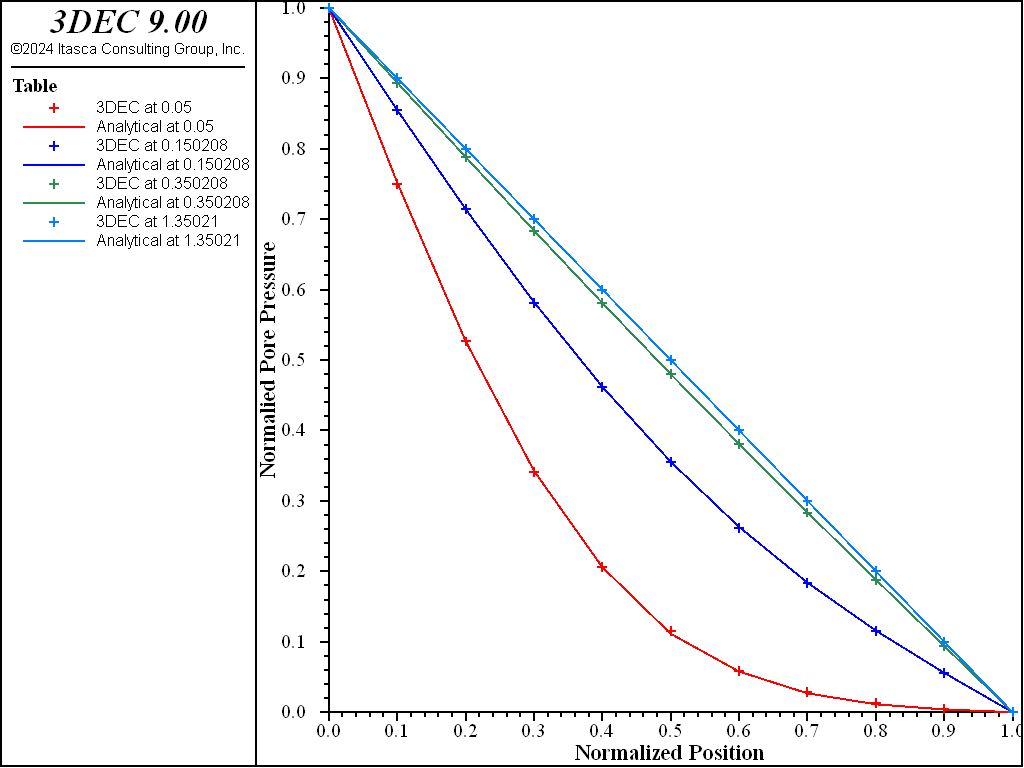
Figure 9: Comparison of excess pore pressures for the explicit solution algorithm (analytical values = lines; numerical values = crosses).
One-Dimensional Consolidation
A saturated layer of soil of thickness \(H\) = 20 m (shown in Figure 10) and large horizontal extent rests on a rigid impervious base. A constant surface load, \(p_z\) = 105 Pa, is applied on the layer under undrained conditions. The soil matrix is homogeneous and behaves elastically; the isotropic Darcy’s transport law applies. The applied pressure is initially carried by the fluid, but as time goes on, the fluid drains through the layer surface, transferring the load to the soil matrix. The solution to this one-dimensional consolidation problem may be expressed in the framework of the Biot theory (see Detournay and Cheng 1993).
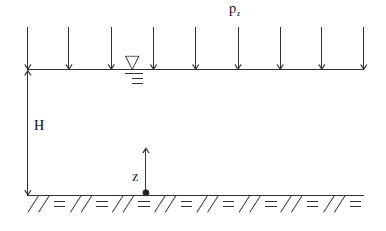
Figure 10: One-dimensional consolidation.
The diffusion equation for the pore pressure, \(p\), has the form
where:
\(c\) = \(k / S\) ;
\(S\) = \({{1}\over{M}} + {{\alpha^2}\over{\alpha_1}}\) = the storage coefficient;
\(\alpha_1\) = \(K + {{4}\over{3}} G\) ;
\(M\) = is the Biot modulus; and
\(\alpha\) = is the Biot coefficient.
The boundary conditions are \(\sigma_{zz} = -p_z H(t)\) and \(p\) = 0 at \(z = H\) (\(H(t)\) is the step function), and \(u_z\) = 0 and \({{\partial p}\over{\partial z}}\) = 0 at \(z\) = 0.
Because the stress is constant, Equation (60) reduces to
with boundary conditions \(p\) = 0 at \(z = H\), and \({{\partial p}\over{\partial z}}\) = 0 at \(z\) = 0.
The initial value, \(p_0\), for the pore pressure induced from loading of the layer may be derived from the fluid constitutive law (\(p = M(\zeta - \alpha {\epsilon}_{zz})\)) by considering undrained conditions (\(\zeta\) = 0) and using the one-dimensional mechanical constitutive law (\({\sigma}_{zz} = \alpha_1 {\epsilon}_{zz} - \alpha p\)) to express strain in terms of stresses. It is given by
The solution for the pore pressure is
where:
\(\hat{p}\) = \({{p}\over{p_z}}\);
\(a_m\) = \({{\pi}\over{2}} (2 m +1)\);
\(\hat{z}\) = \({{H-z}\over{H}}\); and
\(\hat{t}\) = \({{ct}\over{H^2}}\).
The vertical displacement, \(u_z\), is found by considering the equilibrium equation \(\partial {\sigma}_{zz} / \partial z\) = 0, together with the mechanical constitutive equation \({\sigma}_{zz} = \alpha_1 {\epsilon}_{zz} - \alpha p\). By expressing \({\epsilon}_{zz}\) as \(\partial u_z / \partial z\), we obtain upon integration, taking Equation (63) and the boundary conditions into account,
here \({\hat{u}}_z\) is defined as \({\hat{u}}_z = {{\alpha_1 u_z}\over{H p_z}}\).
Several properties are prescribed for this example:
dry bulk modulus, \(K\) |
5 × 108 Pa |
dry shear modulus, \(G\) |
2 × 108 Pa |
Biot modulus, \(M\) |
4 × 109 Pa |
Biot coefficient, \(\alpha\) |
1.0 |
permeability, \(k\) |
10-10 \({m^2}\over{Pa-sec}\) |
The 3DEC model grid for this problem is a column of 20 zones of unit dimensions lined up along the \(z\)-axis. (See Figure 11.) The base of the column is fixed, and lateral displacements are restricted in the \(x\)- and \(y\)-directions. A mechanical pressure, \(p_z\), is applied at the top of the column.
At first, flow is prevented and the model is stepped to equilibrium to establish the initial undrained conditions. At the end of this stage, the stress \({\sigma}_{zz}\) has the value \(-p_z\), in equilibrium with the applied pressure, and the pore pressure has the initial undrained value \(p_0 = \alpha p_z/\alpha_1 S\) (see Equation (62)). Drainage is then allowed by setting the pore pressure to zero at the top of the column. The 3DEC model is cycled to a flow time of 5000 seconds, which is approximately the magnitude of the characteristic time, \(t_c = H^2/c\), for this problem.
The analytical solution for the pore pressure, \(\hat{p}\), and vertical displacement, \({\hat{u}}_z\), at the column mid-height are evaluated using FISH functions, and compared to the numerical solution as time proceeds. The results are plotted versus fluid-flow time in Figures 12 and 13. The transfer of pore pressure to effective stress is illustrated in Figure 14, where the evolutions of normalized total stress, \(-{\sigma}_{zz} / p_z\), effective stress, \(-({\sigma}_{zz} + p) / p_z\), and pore pressure, \(p / p_z\), with fluid-flow time are presented. The 3DEC data file is listed in Example “consolidation.dat – one-dimensional consolidation”. The corresponding project file is located in the “datafiles\Fluid-flow\matrix_flow” folder.
Figure 11: 3DEC grid for one-dimensional consolidation.
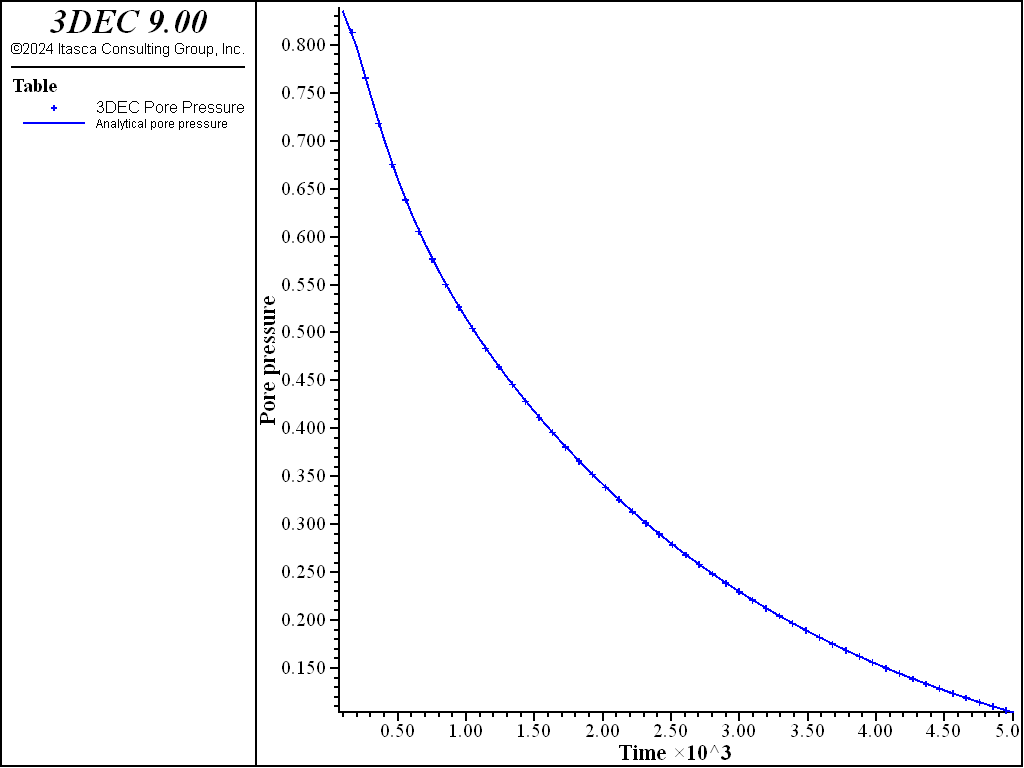
Figure 12: Comparison between analytical and numerical values of pore pressure halfway up the column in a 1D consolidation test.
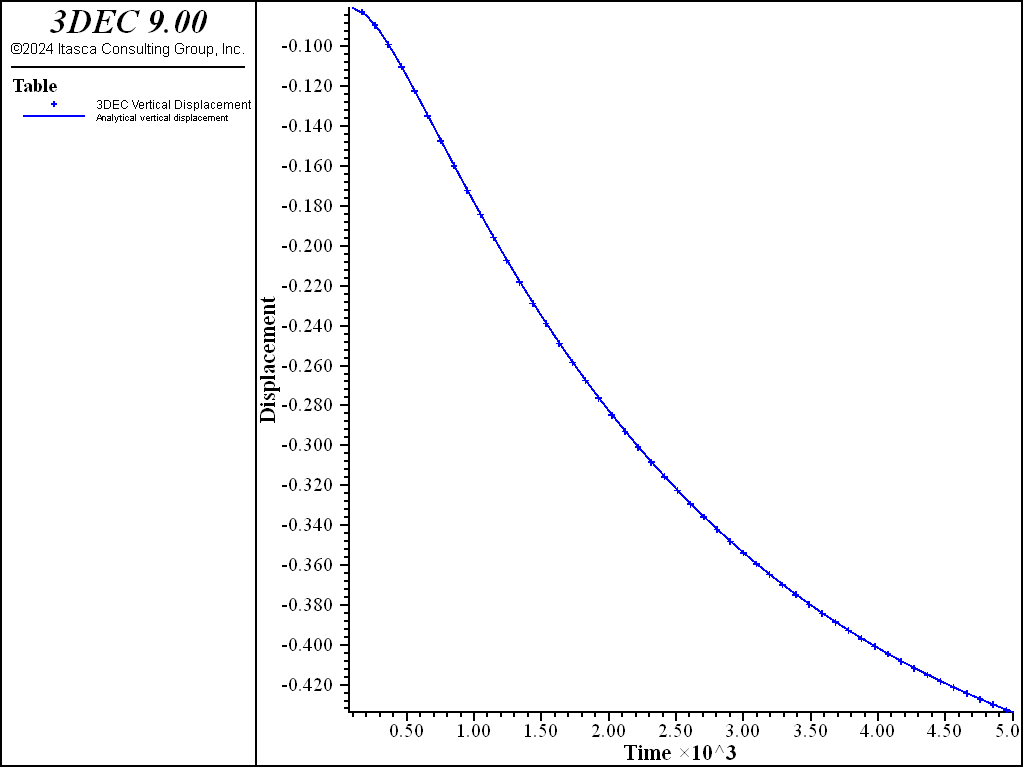
Figure 13: Comparison between analytical and numerical values for vertical displacement halfway up the column in a 1D consolidation test.
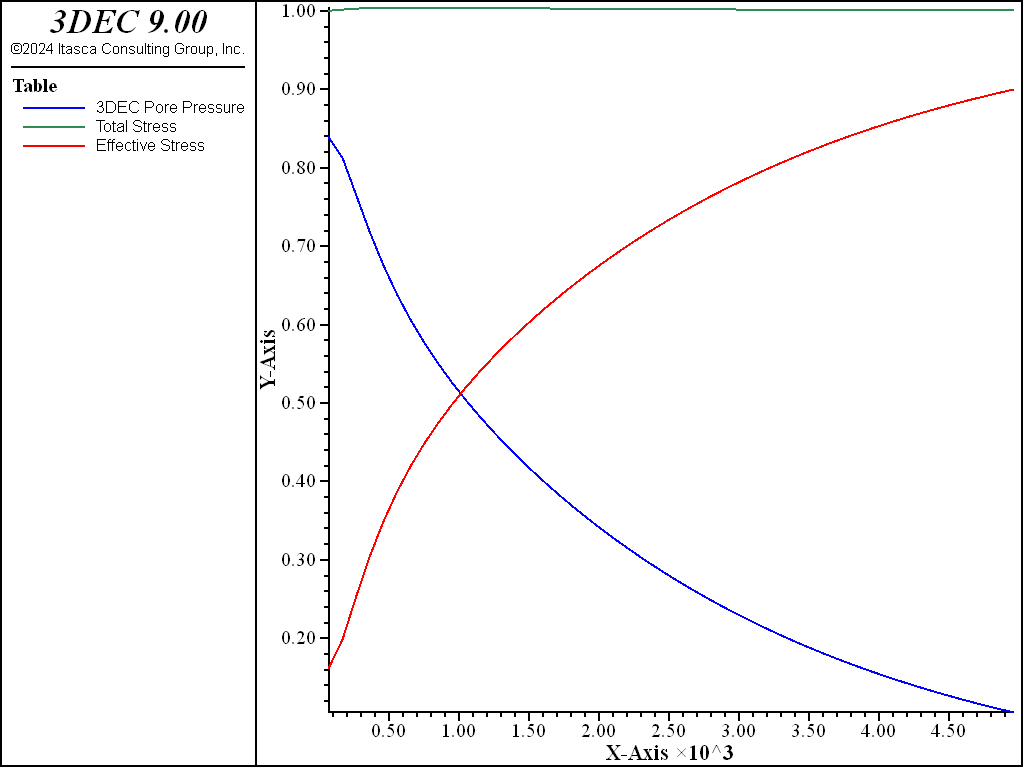
Figure 14: Evolution of pore pressure, total and effective stresses in a 1D consolidation test.
consolidation.dat – one-dimensional consolidation
model new
fish automatic-create off
model title "One-dimensional consolidation (coupled)"
model configure matrixflow
model large-strain off
fish define constants
global c_perm = 1e-10
global c_biotm = 4.e9
global c_bulk = 5.e8
global c_shear = 2.e8
global c_porosity = 0.5
global c_bulkw = c_biotm * c_porosity
local comod = c_bulk + 4. * c_shear / 3.
local storage = 1. / c_biotm + 1.0 / comod
local cv = c_perm / storage
global hh = 20
global bt = cv / (hh * hh)
global pi2 = math.pi * .5
global pz = 1e5
global sig0 = - pz
global p0 = pz / (comod * storage)
global uz0 = pz * hh / comod
end
[constants]
; --- model geometry ---
block create brick 0 1 0 1 0 [hh]
block zone generate edgelength 1
fish define point
global pnt = block.gp.near(0.,0.,10.)
global zpnt = block.zone.near(0.5,0.5,10.5)
global zz = (hh - block.gp.pos.z(pnt)) / hh
end
[point]
;
; --- mechanical model ---
block zone cmodel assign elastic
block zone property bulk [c_bulk] shear [c_shear] density 2000
block gridpoint apply velocity-x 0 velocity-y 0 range position-x -10 10
block gridpoint apply velocity-z 0 range position-z 0
;
block face apply stress-zz [sig0] range position-z 20
;
; --- fluid flow model ---
block zone fluid property permeability [c_perm]
block zone fluid property porosity [c_porosity]
block fluid property bulk [c_bulkw]
;
; --- fish function ---
fish define pp10
pp10 = block.gp.pp(pnt) / pz
global ft = fluid.time.total
global c_szz = block.zone.stress.zz(zpnt) / sig0
global c_eszz = (block.zone.stress.zz(zpnt) + block.zone.pp(zpnt)) / sig0
global c_uz = block.gp.disp.z(pnt) / uz0
global ftbt = ft*bt
end
; --- histories ---
fish history pp10
fish history c_szz
fish history c_eszz
fish history c_uz
fish history ft
fish history ftbt
;
; --- first establish undrained response ---
model fluid active off
model solve ratio 1e-4
model save 'consol-undrained'
;
; --- drained response ---
history purge
flowknot apply pore-pressure 0 range position-z 20
model fluid active on
history interval 2000
model mechanical follower on
model mechanical substep 1
;
model solve fluid time-total 5000
;
;
history export '1' vs '5' table '1'
history export '4' vs '5' table '2'
history export '2' vs '5' table '3'
history export '3' vs '5' table '4'
;
table '1' label '3DEC Pore Pressure'
table '2' label '3DEC Vertical Displacement'
table '3' label 'Total Stress'
table '4' label 'Effective Stress'
;
program call 'analytical.fis'
model save 'consol-drained'
program return
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Apr 02, 2024 |
