Burger’s Contact Model: Stress Relaxation
Problem Statement
Note
The project file for this example may be viewed/run in PFC.[1] The data files used are shown at the end of this example.
The Burger’s Model is exercised with a simple system consisting of two balls fixed with a non-zero initial overlap. The time-decay of the normal force is compared against the expected analytical solution.
Analytical Solution
Consider the stress relaxation condition (i.e., the response of the contact force to the unit displacement). For convenience, eq. (5) in the Burger’s model description is reshown below:
where:
with symbols \(\pm\) and \(\mp\) corresponding to the cases of normal and shear direction, respectively (For example, \(\pm\) means \(+\) for normal direction and \(-\) for shear direction.).
The Laplace transform of (1) is given by (3) under the initial condition of \(\dot{u} = u = 0\), \(\dot{f} = f = 0\).
where \(U(s) = \mathcal{L}[u(t)]\) and \(F(s) = \mathcal{L}[f(t)]\).
The transfer function of the system is given by:
For the unit input \(u(t)= 1\) therefore \(U(s) = 1/s\), the response is given by:
which is expressed by:
where \(z_1\) and \(z_2\) are the roots of the quadratic equation \(a_2 s^2 + a_1 s + 1 = 0\), and
Therefore, the analytical solution of time domain for inputting a unit displacement \(u(t)=1\) is given by:
PFC Model
Numerical simulations are conducted in PFC2D and PFC3D with the datafiles shown below. The two systems are identical; they consists in two balls of equal radius of 0.05 and density 2600 kg/m3 , with an initial overlap (i.e. a step input) of \(u(t=0) = 0.01\). The only difference resides in the shape of the particles: spheres in 3D and unit-thickness disks in 2D, which reflects in the mass and timesteps in the systems being different.
Figures 1 and 2 show the time-decay of the normal force calculated by PFC, compared to the analytical solution. In both models, the numerical solution shows that the contact force exponentially decreases as time increases, which coincides with the analytical solution shown by the blue dashed line in the figures.
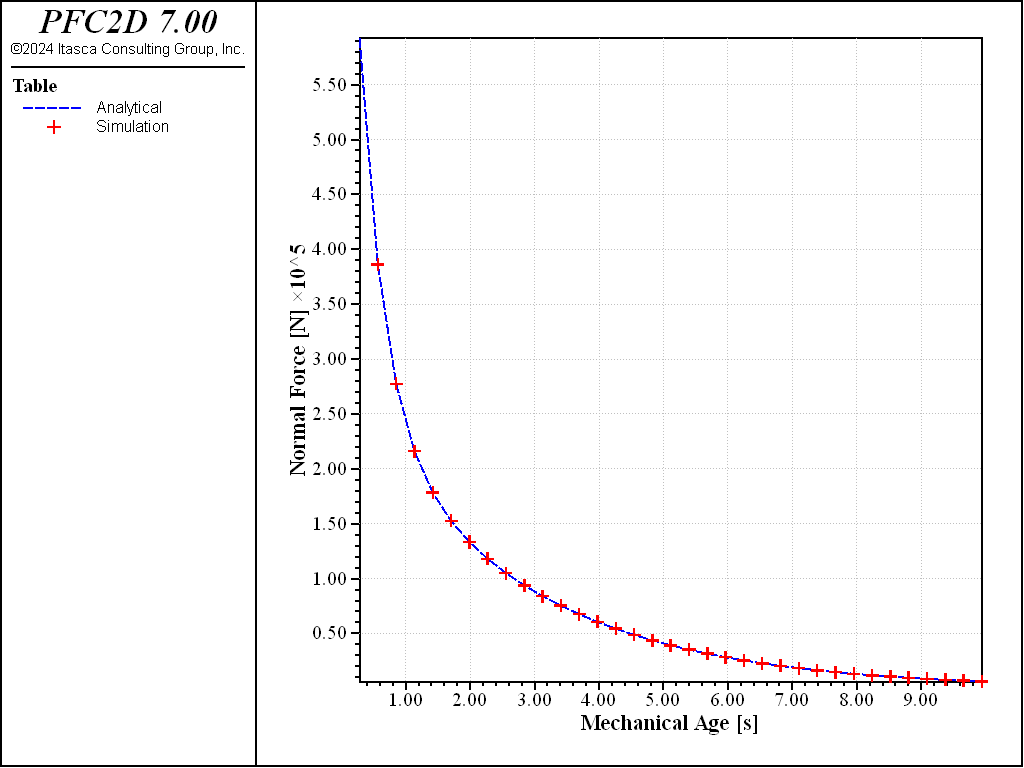
Figure 1: Time history of normal contact force of Burger’s model. The simulation results are shown in red marks, the analytical solution with the blue dashed line (2D model).
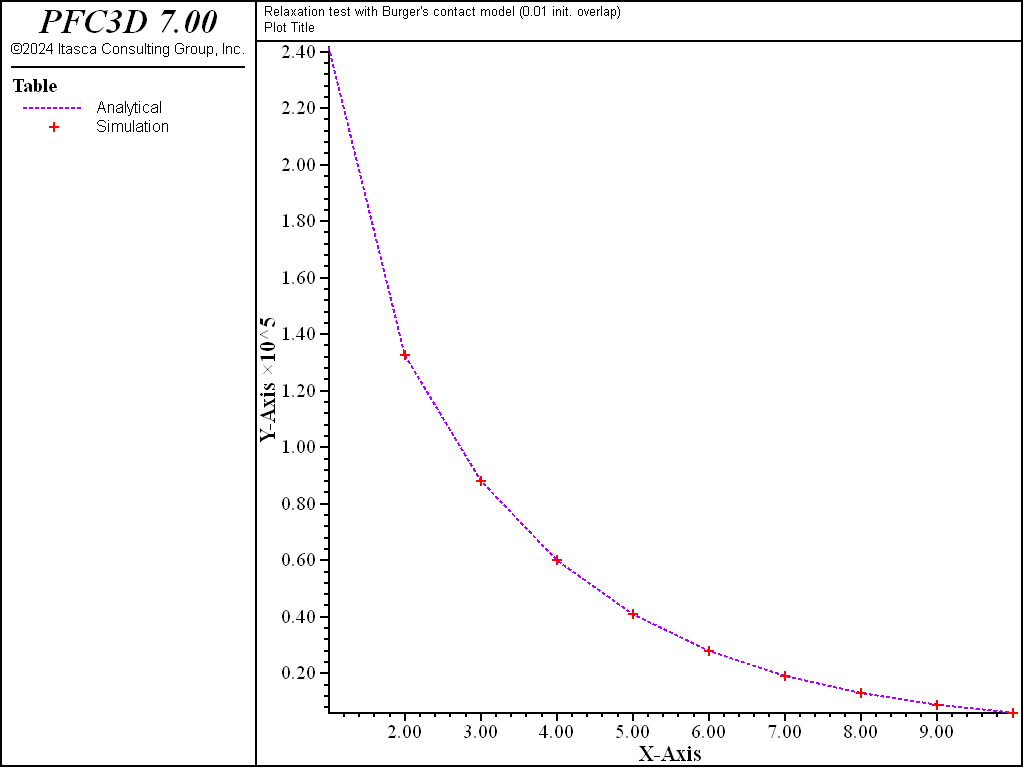
Figure 2: Time history of normal contact force of Burger’s model. The simulation results are shown in red marks, the analytical solution with the blue dashed line (3D model).
Data Files
burger.dat (2D)
;=========================================================================
; fname: burger.dat (2D)
;
; Relaxation test with Burger's contact model (initial overlap of 0.01)
;=========================================================================
model new
model large-strain on
;---------------------------
[k_set = 1.0e8]
[c_set = 1.0e8]
[f_set = 0.0 ]
[rad = 0.05 ]
[un = 0.01 ]
;---------------------------
fish define cal_cf
global cpnt, age0
cal_cf = comp.x(contact.prop(cpnt,'bur_force'))
cal_age = mech.time.total - age0
end
;---------------------------
fish define compare_func
local numPnt = table.size(1)
global errmax = 0.0
local a1 = c_set/k_set + c_set * (1.0/k_set + 1.0/k_set)
local a2 = c_set*c_set/(k_set*k_set)
local b1 = c_set
local b2 = c_set*c_set/k_set
local z1 = (-a1+math.sqrt(a1*a1-4.0*a2))/(2.0*a2)
local z2 = (-a1-math.sqrt(a1*a1-4.0*a2))/(2.0*a2)
local aa1 = (b2*z1+b1)/a2/(z1-z2)
local aa2 = (b2*z2+b1)/a2/(z2-z1)
loop n (1,numPnt)
local tt = table.x(1,n)
table.x(2,n) = table.x(1,n)
table.y(2,n) = un*(aa1*math.exp(z1*tt)+aa2*math.exp(z2*tt))
errmax = math.max(errmax,math.abs(table.y(1,n)-table.y(2,n))/table.y(2,n))
endLoop
io.out(string.build(' Max. error = %1 %',string(errmax*100)))
end
;=====================================
contact cmat default model burger property ...
'bur_knk' [k_set] 'bur_cnk' [c_set] ...
'bur_knm' [k_set] 'bur_cnm' [c_set] ...
'bur_ksk' [k_set] 'bur_csk' [c_set] ...
'bur_ksm' [k_set] 'bur_csm' [c_set] ...
'bur_fric' [f_set]
; --- Create two balls, assign properties and BCs.
model domain extent -1 1
ball create id 1 rad [rad] position-y 0.0
ball create id 2 rad [rad] position-y [2.0*rad-un]
ball attribute density 2600.0
ball fix velocity-x velocity-y spin
model clean
[cpnt = contact.find('ball-ball',1)]
;
fish history name '1' cal_cf
fish history name '2' cal_age
history interval = 1000
[age0 = mech.time.total]
model mechanical timestep fix 2.840299219037086e-04
model solve time 10.0
history export '1' vs '2' table '1'
[compare_func]
model save 'system-final'
program return
;=========================================================================
; eof: burger.dat (2D)
burger.dat (3D)
;=========================================================================
; fname: burger.p3dat
;
; Relaxation test with Burger's contact model (0.01 init. overlap)
;=========================================================================
model new
model large-strain on
model title 'Relaxation test with Burger\'s contact model (0.01 init. overlap)'
;---------------------------
[k_set = 1.0e8]
[c_set = 1.0e8]
[f_set = 0.0 ]
[rad = 0.05 ]
[un = 0.01 ]
;---------------------------
fish define cal_cf
global cpnt, age0
cal_cf = comp.x(contact.prop(cpnt,'bur_force'))
cal_age = mech.time.total - age0
end
;---------------------------
fish define compare_func
local numPnt = table.size(1)
global errmax = 0.0
local a1 = c_set/k_set + c_set * (1.0/k_set + 1.0/k_set)
local a2 = c_set*c_set/(k_set*k_set)
local b1 = c_set
local b2 = c_set*c_set/k_set
local z1 = (-a1+math.sqrt(a1*a1-4.0*a2))/(2.0*a2)
local z2 = (-a1-math.sqrt(a1*a1-4.0*a2))/(2.0*a2)
local aa1 = (b2*z1+b1)/a2/(z1-z2)
local aa2 = (b2*z2+b1)/a2/(z2-z1)
loop n (1,numPnt)
local tt = table.x(1,n)
table.x(2,n) = table.x(1,n)
table.y(2,n) = un*(aa1*math.exp(z1*tt)+aa2*math.exp(z2*tt))
errmax = math.max(errmax,math.abs(table.y(1,n)-table.y(2,n))/table.y(2,n))
endLoop
io.out(string.build(' Max. error = %1 %',string(errmax*100)))
end
;=====================================
contact cmat default model burger property ...
bur_knk [k_set] bur_cnk [c_set] ...
bur_knm [k_set] bur_cnm [c_set] ...
bur_ksk [k_set] bur_csk [c_set] ...
bur_ksm [k_set] bur_csm [c_set] ...
bur_fric [f_set]
; --- Create two balls, assign properties and BCs.
model domain extent -1 1
ball create id 1 rad [rad] position-z 0.0
ball create id 2 rad [rad] position-z [2.0*rad-un]
ball attribute density 2600.0
ball fix velocity-x velocity-y velocity-z spin
model clean
[cpnt = contact.find('ball-ball',1)
;
fish history cal_cf
fish history cal_age
history interval = 1000
model mechanical timestep fix 1e-3
[age0 = mech.time.total]
model solve time 10.0
history export '1' vs '2' table '1'
[compare_func]
model save 'system-final'
program return
;=========================================================================
; eof: burger.p3dat
Endnotes
| [1] | To view this project in PFC, use the program menu.
⮡ PFC |
| Was this helpful? ... | PFC © 2021, Itasca | Updated: Feb 25, 2024 |
