Array Style Programming with PFC and NumPy
An alternative NumPy array-based interface to PFC is also provided.
Instead of dealing with individual Ball objects, the array interface deals with the attributes and properties of all balls simultaneously.
Note
NumPy is an extension to Python which defines a powerful array object and many useful numerical operations. Using NumPy and array style programming can be much faster than looping natively in Python. The style of programming is different from that defined in the object-oriented interface.
For more information about NumPy see: http://numpy.org
import itasca as it
it.command ("python-reset-state false")
from itasca import ballarray as ba
import numpy as np
First, we import the itasca, ballarray and numpy modules.
Note that the ballarray module is a submodule of the itasca
module. To shorten the typing required we import these modules as a
shortened name.
Next, we create a simple model as before,
dim = 2.5e-2
rad = dim / 20.0
it.command("""
model new
model large-strain on
model domain extent -5e-2 6e-2 -6e-2 5e-2 -5e-2 5e-2
contact cmat default model linear property kn 1e1 dp_nratio 0.2
ball generate cubic box -{xdim} {xdim} -{ydim} {ydim} -{xdim} {xdim} rad {rad}
ball attribute dens 2600
""".format(xdim=dim-rad, ydim=2*dim-rad, rad=rad))
Scalar Arrays
Now we call the radius function defined in the ballarray module.
radii = ba.radius()
radii
- output:
[ 0.00125 0.00125 0.00125 ..., 0.00125 0.00125 0.00125]
Note
When a large array is printed out in the terminal, only the beginning and ending of the array is shown. The ellipsis shows the gap.
The variable radii is an array of all the ball radii. Next we test that this is indeed an array and check that it has the correct shape.
assert type(radii) is np.ndarray
print (radii.shape)
print (it.ball.count(),)
- output:
(16000,) 16000
We set the ball radii to 75% smaller and update the radii values.
- Methods starting with
set_in the array interface are used to send values back to PFC. - Simply changing the
radiusarray only changes our copy of the data. - Arrays used to set model values must have the correct shape. In this case they must be a one-dimensional array of length equal to the number of balls.
radii *= 0.75
ba.set_radius(radii)
radii = ba.radius()
radii
- output:
[ 0.0009375 0.0009375 0.0009375 ..., 0.0009375 0.0009375 0.0009375]
Multidimensional Arrays
Here we define a variable positions which contains a
multidimensional array of the ball positions.
positions = ba.pos()
positions
- output:
[[-0.02375 -0.04875 -0.02375] [-0.02125 -0.04875 -0.02375] [-0.01875 -0.04875 -0.02375] ..., [ 0.01875 0.04875 0.02375] [ 0.02125 0.04875 0.02375] [ 0.02375 0.04875 0.02375]]
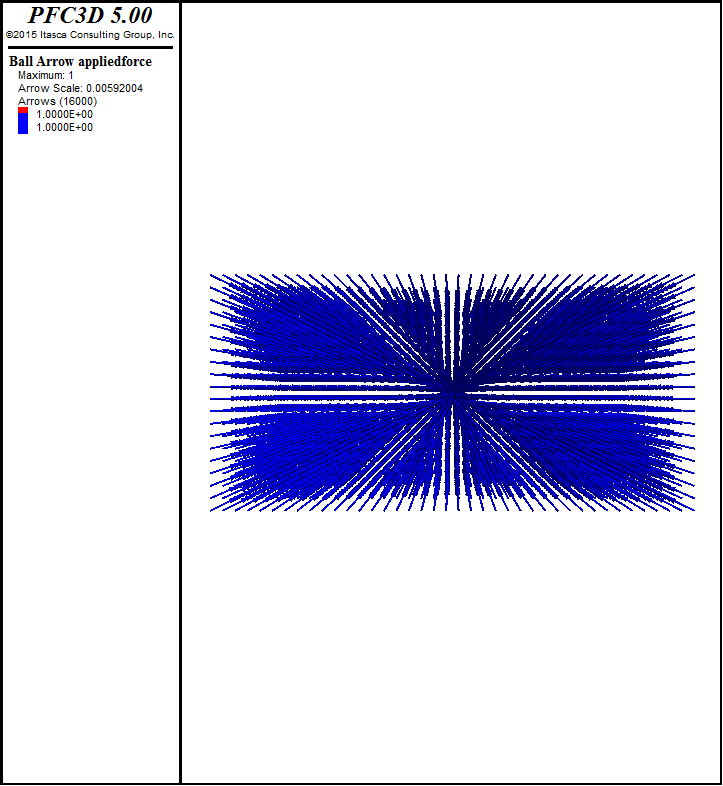
As an example we will apply a 5e-3 N force to each ball in the
direction toward the origin. The origin is in the middle of the model so the
force vectors will point inward. First we define a new array force
force = -5e-3 * (positions.T/np.linalg.norm(positions,axis=1)).T
force
- output:
[[ 0.0020059 0.00411737 0.0020059 ] [ 0.00182427 0.00418509 0.00203889] [ 0.00163391 0.00424817 0.00206962] ..., [-0.00163391 -0.00424817 -0.00206962] [-0.00182427 -0.00418509 -0.00203889] [-0.0020059 -0.00411737 -0.0020059 ]]
then use the ballarray interface to set this as the applied force to each ball.
ba.set_force_app(force)
The following image shows this force applied to each particle in the direction of the origin.
It is often useful to get individual (one-dimensional) arrays for each component direction.
x, y, z = positions.T
y
- output:
[-0.04875 -0.04875 -0.04875 ..., 0.04875 0.04875 0.04875]
Note
The arrays referred to by x, y and z are array views
which means they are references to the data in the positions
variable. Changing x will change the values in the variable
positions. This is an optimization that avoids copying but can
be confusing.
NumPy arrays support comparison operators which return mask arrays,
y>0
- output:
[False False False ..., True True True]
which are arrays of True or False values.
Mask arrays can be used in assignments. In the example below, we set the radii of all the balls in the positive y half-space back to the origional size.
radii[y>0] /= 0.75
ba.set_radius(radii)
The following image shows the updated ball radii.
Ball Creation
The ballarray module also provides a create method that can be used for fast creation of balls in the model.
This methods takes a one-dimensional array of scalars to specify radii as first argument, and {two-dimensional in 2D;
three-dimensional in 3D} array of scalars to specify positions as second argument. The function also accepts optional
arguments that allows to specify attributes and properties for the created balls. These optional arguments accept scalars
or arrays with consistent dimensions.
For instance, the following lines create a collection of 100000 balls with random radii and random positions
from vec import vec
nballs = 100000
rmin = 8.0e-4
rmax = 1.2e-3
dom_lo = vec((-5e-2,-6e-2,-5e-2))
dom_hi = vec(( 6e-2, 5e-2, 5e-2))
brad = rmin + np.random.rand(nballs) *(rmax-rmin)
bpos = dom_lo + np.random.rand(nballs,3) *(dom_hi-dom_lo)
ba.create(brad,bpos)
Note that the create method simply uses the input radii and positions, and does not check that balls do not overlap.
The following lines demonstrate how optional arguments can be specified as well, in this case the density and the local damping coefficient.
it.command("ball delete")
ba.create(brad,bpos,density=1000.0,damp=0.7)
In the line above, both density and damping are specified with constant scalar values. Arrays of consistent shapes can also be used as demonstrated below where density is specified as a one-dimensional array.
bdens = np.full_like(brad,1000.0)
x,y,z = bpos.T
bdens[x<0] *= 2.0
it.command("ball delete")
ba.create(brad,bpos,density=bdens,damp=0.7)
Properties can also be specified with the props optional arguments, that expects a dictionary structure as demonstrated below.
it.command("ball delete")
ba.create(brad,bpos,density=bdens,damp=0.7,props={'kn':1e4,'ks':1e4})
it.command("ball delete")
kn = np.full_like(brad,1.0e4)
kn[z<0] = 2e4
ba.create(brad,bpos,density=bdens,damp=0.7,props={'kn':kn,'ks':1e4,'myprop':'george'})
Example File
The source code for the examples here is array_interface.py.
| Was this helpful? ... | 3DEC © 2019, Itasca | Updated: Feb 25, 2024 |