30.0 - Update Spatial Searching Data Structures
The model domain has been introduced to streamline spatial searching and simplify some commonly performed simulation tasks. The domain is a box aligned with the global coordinate system where all PFC model components exist. The domain is decomposed into equidimensional boxes, or cells, for proximity detection, and each cell holds a list of pieces that overlap it in some sense. The resulting data structure is termed a cell space. Such data structures can significantly reduce the computational overhead of delineating objects in a region of space because one must only query the cells in the region of interest. When using a cell space, spatial proximity can be determined for all objects in a time that is proportional to the number of objects. In comparison, testing each object against one another for proximity takes a time that is proportional to the square of the number of objects, which is a very computationally intensive proposition. As contacts are created/deleted during cycling based on piece proximity, the act of contact detection relies heavily on an efficient cell space implementation.
During this cycle point, all cell space data structures holding pieces are validated so that contact detection can be accomplished during the following cycle point. Each piece is abstracted for spatial searching by a set of axis-aligned bounding boxes termed extents. Extents are used to expedite the process of determining which cells a piece may overlap. Prior to describing the cell space implementation in detail, the piece extent concept is expanded upon below.
Piece Extents
The minimum extent of a piece is the smallest axis-aligned bounding box that completely encloses the piece as shown below.
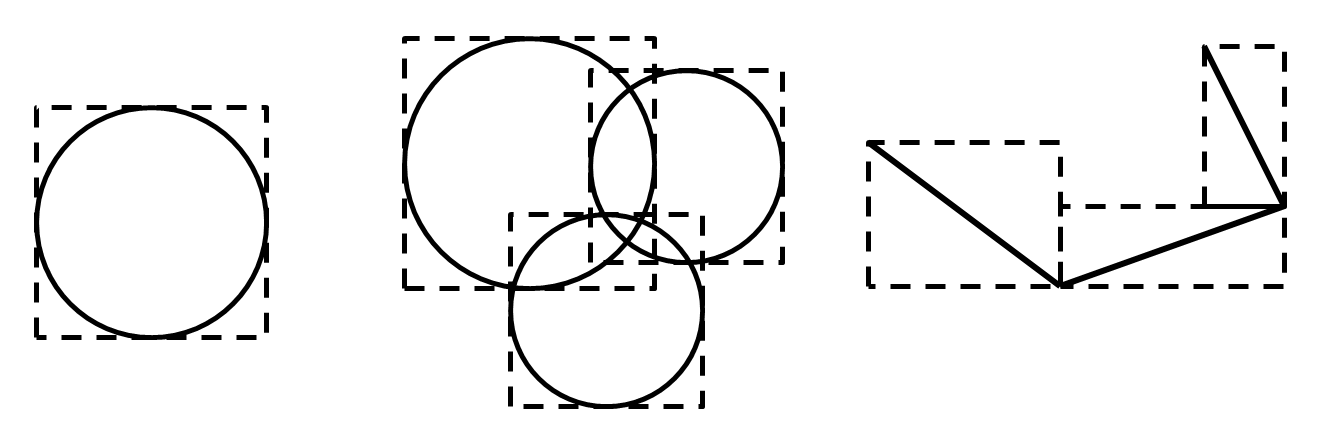
Figure 1: Minimum extents for a ball (left), pebbles of a clump (center) and facets of a wall (right).
If pieces were mapped into cells based solely on their minimum extents, one could not guarantee that contacts would be created prior to the cycle when forces may develop between pieces. This is problematic because large forces may exist during a single cycle, leading to model instability. In PFC, we can guarantee that contacts are created prior to the cycle that forces develop by mapping pieces into the cell space using an enlarged extent and limiting the piece translation during a cycle. This guarantee holds provided that either the automatic or scaled timestep determination mode is active. See the “Timestep Determination” section for more information about these modes and this subsection for a detailed description of the kinematic constraint on piece motion. This guarantee is elaborated upon in the “Contact Update” section.
The minimum extent is enlarged in each direction by a contact detection tolerance factor
\(\varepsilon\), that can be specified by the user (see the ball tolerance,
clump tolerance, rblock tolerance, and wall tolerance commands). This tolerance, calculated when the
piece is mapped into the cell space, is given by:
where \(\left | \mathbf{v} \right |\) is the magnitude of the translational velocity of the piece, \(\Delta t\) is the current timestep, and \(E_p\) is a measure of the size of the piece. \(E_p\) is the diameter of the ball or pebble while, for facets, \(E_p\) is the average length of the minimum extent sides. \(\varepsilon_v\) is set with the velocity keyword, \(\varepsilon_e\) is set with the extent keyword and \(\varepsilon_c\) is set with the constant keyword.
Pieces are mapped into the cell space based on their cell extents, shown in the following
figure. As pieces move, they are remapped into the cell space (i.e., removed from the cells into
which they were previously mapped and mapped into the appropriate cells). Remapping is triggered
whenever the piece cumulatively moves more than \(\varepsilon\) in any direction from its position when
it was last mapped into the cell space. For pebbles and facets, one must account for cumulative
movement, including rotation about either the clump centroid or the wall center of rotation. The
maximum interaction distance, \(\overline{r}_i\), is specified with the proximity keyword in
either the cmat add, cmat default, or cmat modify commands. This allows for
interactions at a distance to be modeled with PFC by increasing the cell extent so that pieces
farther apart can be detected as in proximity with one another. The maximum of all interaction
distances specified in the Contact Model Assignment Table (CMAT) is used for all pieces.
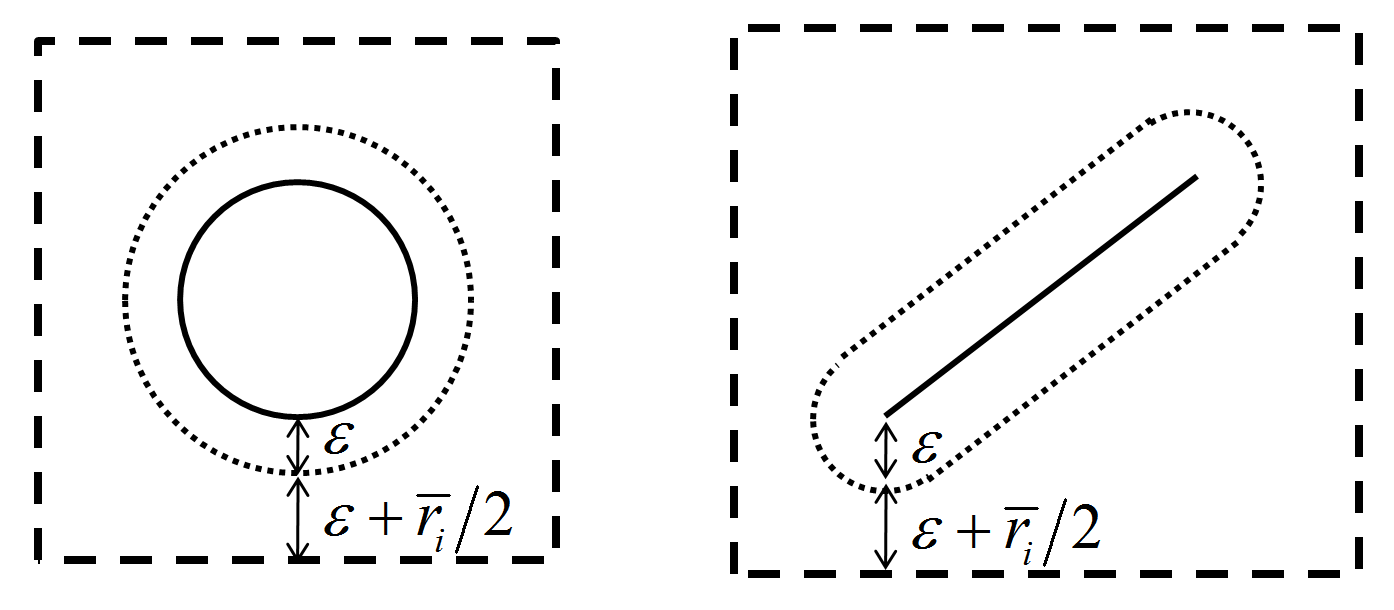
Figure 2: Cell extents for a ball/pebble and a facet. \(\varepsilon\) is the tolerance, and \(\overline{r}_i\) is the maximum interaction distance.
When pieces are extended, their cell extents may overlap many more cells than are appropriate for efficient spatial proximity detection. As shown in the “Contact Update” section, one would ideally want to search for pieces within a distance of \(2 \varepsilon + \frac{\overline{r}_i}{2}\) of a dirty piece for potential contacts. To alleviate mapping pieces into cells outside of this distance, a conformal surface check is used. One may think of a conformal surface as consisting of all points \(2 \varepsilon + \frac{\overline{r}_i}{2}\) from the surface of the piece as shown below. A piece is thus mapped into the cells that its conformal surface overlaps, which is a subset of the cells that its cell extent overlaps.
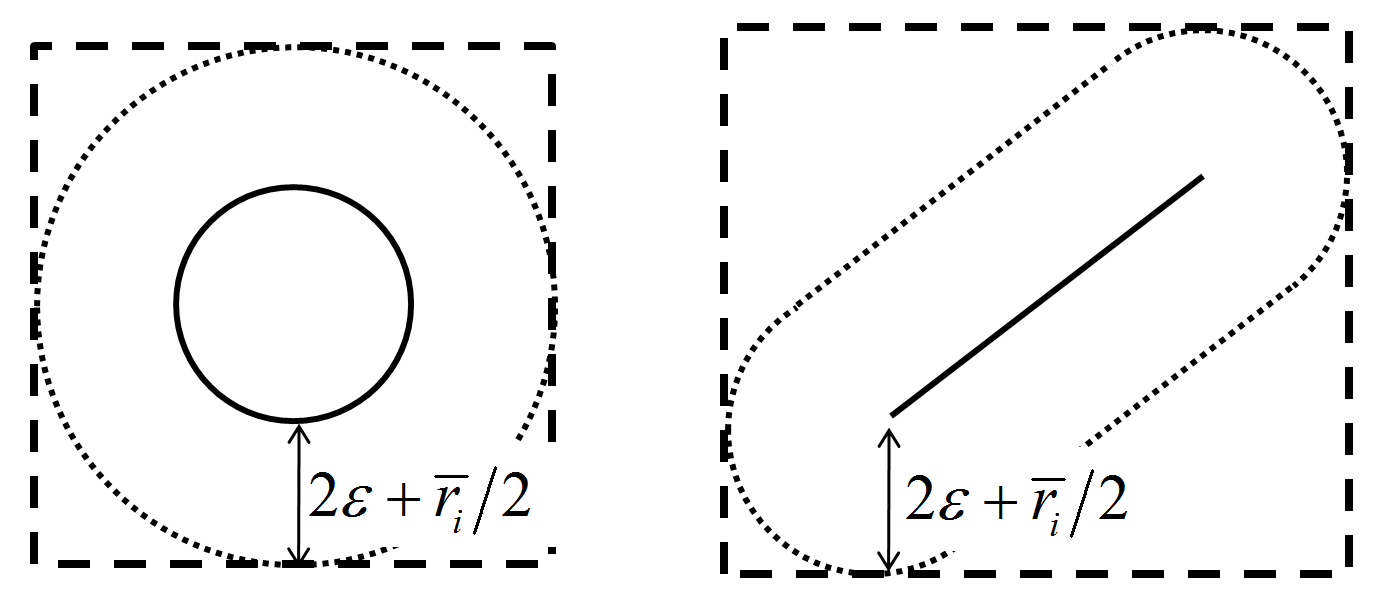
Figure 3: Conformal surface for a ball/pebble and a facet. \(\varepsilon\) is the tolerance, and \(\overline{r}_i\) is the maximum interaction distance.
Cell Space
Once the model-domain dimensions have been specified, the space is subdivided into \(N\) equidimensional parent cells, each with side length \(len\). By default there are {1,000 in 2D; 10,000 in 3D} parent cells. The list of parent cells is held in a one-dimensional array of length \(N\). Each parent cell holds a list of objects that are mapped into that cell. As the pieces are initially generated, their cell extents are calculated and they are deemed dirty. PFC adopts a method similar to the [Yao2004] approach, where pieces are dirty upon creation or during a cycle if remapping is required. A dirty list is constructed so that only those pieces requiring remapping are operated upon during this cycle point. Such a local remapping scheme is highly advantageous in bonded-particle simulations where few pieces require remapping during any given cycle. [Yao2004] demonstrate that, for molecular-dynamics simulations, local remapping can be more efficient than global remapping as well. The underlying data structure supporting spatial searching must, as a result, be easily modifiable at the local level to take advantage of local remapping.
One can determine into which parent cells a piece may be mapped by intergerizing the upper and lower bounds of its cell extent in each dimension
where the the vector \(\mathbf N\) contains the number of cells in each dimension, the vector \(\mathbf {cextent}_{\rm lb}\) contains the lower bound of the cell extent, the vector \(\mathbf {cextent}_{\rm ub}\) contains the upper bound of the cell extent, the vector \(\mathbf x_0\) is the origin of the cell space and the vectors \(\mathbf {ind}_{\rm lb}\), and \(\mathbf {ind}_{\rm ub}\) are the lower and upper indices of the cells in each dimension, respectively. The \(\lfloor \rfloor\) operator is the floor function. Given the vector integer indices, \(\mathbf {ind}\), falling between \(\mathbf {ind}_{\rm lb}\) and \(\mathbf {ind}_{\rm ub}\) in each dimension, the index of the corresponding parent cell in the one-dimensional array can be calculated
where \(\mathbf {ind}_{\rm z} = 0\) in 2D and the subscripts denote the components of the vector.
In addition to the list of pieces held by each cell, each piece holds a list of all cells into which it has been mapped. As pieces are mapped into parent cells, the number of pieces with extent centroids lying within each cell is summed along with their extent sizes defined as the extent {areas in 2D; volumes in 3D}. The method described thus far is a linked-cell algorithm. In order to assist with spatial searching, an iterator data structure is implemented so that one can simply and efficiently inspect all pieces within the proximity of a search window.
When more than a specified number of piece-extent centroids map into a single cell, a check is performed to determine whether or not the cell should be refined. Cell refinement refers to partitioning a parent cell into equidimensional child cells. Upon refinement, the parent cell no longer provides access to mapped pieces but instead contains an independent, embedded cell space. A refined cell space has a spatial size equal to the size of the parent-cell extent, a one-dimensional array holding lists of pieces mapped into its cells, and an iterating capability. The goal of the refinement strategy is to scale the cell size locally to accommodate inhomogeneous variations in piece extent sizes automatically and dynamically. The goal is that no user tuning be required to achieve nearly optimal search performance for a wide range of problems. Refinement is indicated if the parent cell size is more than a specified factor of times larger than the average size of piece extents whose centroids map into the parent cell. This test mitigates refinement of a small cell overlapped by pieces with large extents. The parent cell is partitioned into equidimensional cells to match the target number of piece extents per cell.
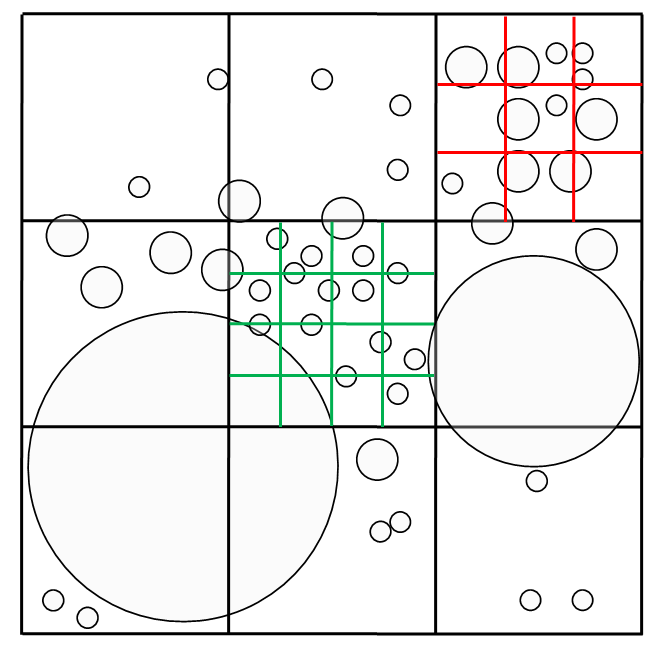
Figure 4: Parent cells are locally refined into children to match a target number of objects in the cell.
As cycling continues, the piece distribution may change so that a refined cell space is no longer effective. For instance, small pieces may migrate through a coarse matrix, flow may change the piece size distribution locally or few pieces may reside in a previously occupied region of space. Refined cells are checked to ensure that extent centroids continue to be mapped into them, and that the average size of the mapped extents remains consistent with the refinement criteria. Violation of either of these conditions indicates that the refined cell space should be deleted, with remaining pieces placed in the parent cell. In this way, the spatial subdivisions can be dynamically regenerated in response to model evolution.
[Mio2007] demonstrated an alternate linked-cell implementation with optimal performance when the number of objects mapped per cell is approximately 1 to 5. The figure below presents the relative performance of the PFC spatial-search implementation described above without refinement; these results are used to guide the cell-refinement algorithm. Approximately 11,000 uniform balls in 3D are generated in a cubical region such that they do not overlap (generated with 100,000 tries). These balls are subsequently enlarged by a factor of 1.5. Gravity is disabled, an initial velocity is supplied to the balls, and the model is cycled for 250 cycles. The extents are enlarged in each direction by 25% of the ball radius. The model domain is set such that ~120,000 ball extents fit within the model domain without overlap. The reported relative slowdown factors are based on the remapping and contact detection times summed while cycling. This measure of performance is referred to as the detection time, where reported values are always averaged over two runs. Optimal schemes have relative slowdown factors of 1 while larger values convey longer detection times. It is evident that 5-20 piece extents per cell are optimal with little performance sensitivity within this range.
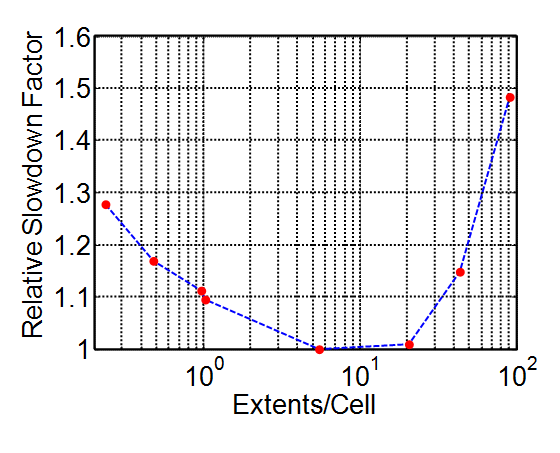
Figure 5: Results showing the relative performance of detection (i.e., remapping plus contact detection) as a function of the number of piece extents that can fit in a cell without overlap for the linked-cell implementation.
As a result of the simulations above, the target number of objects per cell is fixed at 10. Once the condition of more than 10 pieces whose centroids fall within a cell is detected, that cell is tested for refinement. Once fewer than 2 pieces map into a cell and that cell is a child cell, that cell is unrefined. This is accomplished on multiple threads via a wait-free list data structure termed a lazy list similar to [Heller2005].
– Next Cycle Point: Create/delete Contacts –
References
| [Heller2005] | Heller, S., M. Herlihy, V. Luchangco, M. Moir, B. Scherer, and N. Shavit, “A lazy concurrent list-based set algorithm,” In 9th International Conference on Principles of Distributed Systems (OPODIS), Dec. 2005 (2005). |
| [Mio2007] | Mio, H., A. Shimosaka, Y. Shirakawa and J. Hidaka, “Cell optimization for fast contact detection in the discrete element algorithm,” Advanced Powder Technology, 18 (4), 441-453 (2007). |
| [Yao2004] | (1, 2) Yao, Z., J. Wang, G. Liu and M. Cheng, “Improved neighbor list algorithm in molecular simulations using cell decomposition and data sorting method,” Computer Physics Communications, 161, 27-35 (2004). |
| Was this helpful? ... | 3DEC © 2019, Itasca | Updated: Feb 25, 2024 |
