Verification Examples
Slip on a Joint Induced by a Propagating Harmonic Shear Wave
Problem Statement
This problem concerns the effects of a planar discontinuity on the propagation of an incident shear wave. Two homogeneous, isotropic, semi-infinite elastic regions, separated by a planar discontinuity with a limited shear strength, are shown in Figure 1. A normally incident, plane-harmonic shear wave will cause slip at the discontinuity, resulting in frictional energy dissipation. Thus, the energy will be reflected, transmitted and absorbed at the discontinuity. The problem is modeled with 3DEC, and the results are used to determine the coefficients of transmission, reflection and absorption. These coefficients are compared with ones given by an analytical solution (Miller 1978).
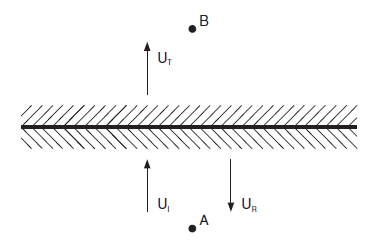
Figure 1: Transmission and reflection of incident harmonic wave at a discontinuity.
Analytic Solution
The coefficients of reflection (R), transmission (T ) and absorption (A) given by Miller (1978) for the case of uniform material are
where \(E_I\), \(E_T\) and \(E_R\) represent the energy flux per unit area per cycle of oscillation associated with the incident, transmitted and reflected waves, respectively. The coefficient \(A\) is a measure of the energy absorbed at the discontinuity. The energy flux \(E_I\) is given by
where:
\(T\) = \((2 \pi) / \omega\) = the period for the incident wave;
\(\sigma_s\) = shear stress;
\(v_s\) = particle velocity in the \(x\)-direction; and
\(\omega\) = frequency of incident wave (radian/sec).
For elastic media,
Hence,
in which \(c\) is the velocity of the propagating shear wave.
The energy flux of the incident wave, \(E_I\), is evaluated at Point A (see Figure 1) for no slip at the discontinuity. The energy flux of the transmitted wave, \(E_T\), is evaluated at Point B for the case of slip at the discontinuity. The energy flux of the reflected wave, \(E_R\), is calculated by determining the difference of velocities in two cases: slip and no slip.
Numerical Model
The numerical results are determined for four values of the dimensionless frequency \(\omega \gamma U/\tau_s\), where \(\gamma = (\rho G)^{1/2}\), \(\tau_s\) = discontinuity cohesion, \(U\) = displacement amplitude of incident wave, \(\rho\) = density of the media, and \(G\) = shear modulus of the media.
The problem geometry modeled by 3DEC is shown in Figure 2. The media were modeled with elastic, fully deformable blocks of height (\(h/ 2\)), width \(b\) and length \(l\). The blocks are separated by a planar discontinuity extending in the \(xz\)-plane. The blocks were internally discretized into tetrahedral zones, as shown in Figure 3. Nonreflecting boundary conditions were used on the top and bottom of the model. Displacements at boundaries along the \(yz\)-plane at \(x\) = 0 and \(x\) = \(b\) were restrained in the \(y\)-direction to simulate plane shear wave conditions. Displacements at boundaries were restrained in the \(z\)-direction along the \(xy\)-plane at \(z\) = 0 and \(z\) = l to simulate the plane-strain condition.
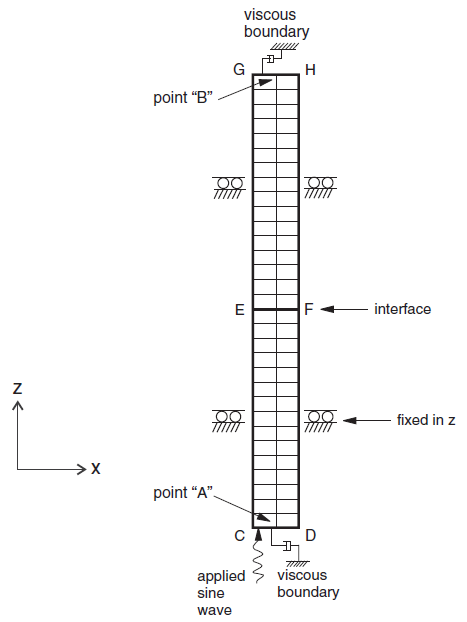
Figure 2: Geometry for the problem of slip induced by harmonic shear.
Material Properties
The material properties of the elastic media and planar discontinuity are given in the following two tables.:
| Mass density density | 2,650 kg/m3 |
| Shear modulus shear | 10,000 MPa |
| Bulk modulus bulk | 16,667 MPa |
| Normal stiffness stiffness-normal | 10,000 MPa/m |
| Shear stiffness stiffness-shear | 10,000 MPa/m |
| Friction angle friction | 0 |
| Cohesion cohesion | 2.5, 0.5, 0.1 and 0.02 MPa |
Dynamic Loading
The harmonic shear stress applied at the bottom boundary has the following characteristics:
maximum stress of incident wave: 1.0 MPa
frequency of incident wave: 1 Hz
type of harmonic wave: sinusoidal
Note that the magnitude of the incident wave must be doubled in the numerical model to account for the simultaneous presence of the nonreflecting boundary.
Results
The analytical solution forwave propagation through a slipping discontinuity (Miller 1978) assumes a Mohr-Coulomb discontinuity failure criterion with constant cohesion. In 3DEC, however, when discontinuity shear and/or tensile strength is exceeded, the cohesion and tension are ignored in all subsequent calculations. Because the analytical solution assumes a constant discontinuity cohesion regardless of stress history, a FISH function which prevents setting cohesion and tension to zero when discontinuity shear and/or tensile strength is exceeded was prepared (see the file “sihsw.fis” below).
An initial run assumed that the discontinuity remains elastic by setting the discontinuity cohesion to 2.5 MPa. A stress wave of amplitude 1 MPa and frequency 1 Hz was applied at the base of the model. It should be noted that the displacements and velocities are determined at the nodal points of the tetrahedron. The stresses, however, are determined at the centroid of the tetrahedron. The time histories of shear stress, velocity and displacement are monitored at Points A (40, 15, −200) and B (40, 15, 200). The linear history of stresses are monitored close to Points A and B. The shear stresses at Points A and B are shown in Figure 4. From the amplitude of the stress history at A and B, it is clear that there was perfect transmission of the wave through the discontinuity. It is also clear from Figure 4 that the nonreflecting boundary condition provides perfect absorption of normally incident waves.
In the next run, the cohesion was lowered to 0.5 MPa to permit slip along the discontinuity. The recorded shear stresses at Points A and B are shown in Figure 5. The peak stress at Point A is the superposition of the incident wave and the wave reflected from the slipping discontinuity. Figure 6 and Figure 7 show the shear stress at Points A and B for a discontinuity cohesion of 0.1 and 0.02 MPa. It can be seen in Figure 5 through Figure 7 that the shear stress of Point B is limited by the discontinuity strength at 0.5, 0.1, and 0.02 MPa, respectively.
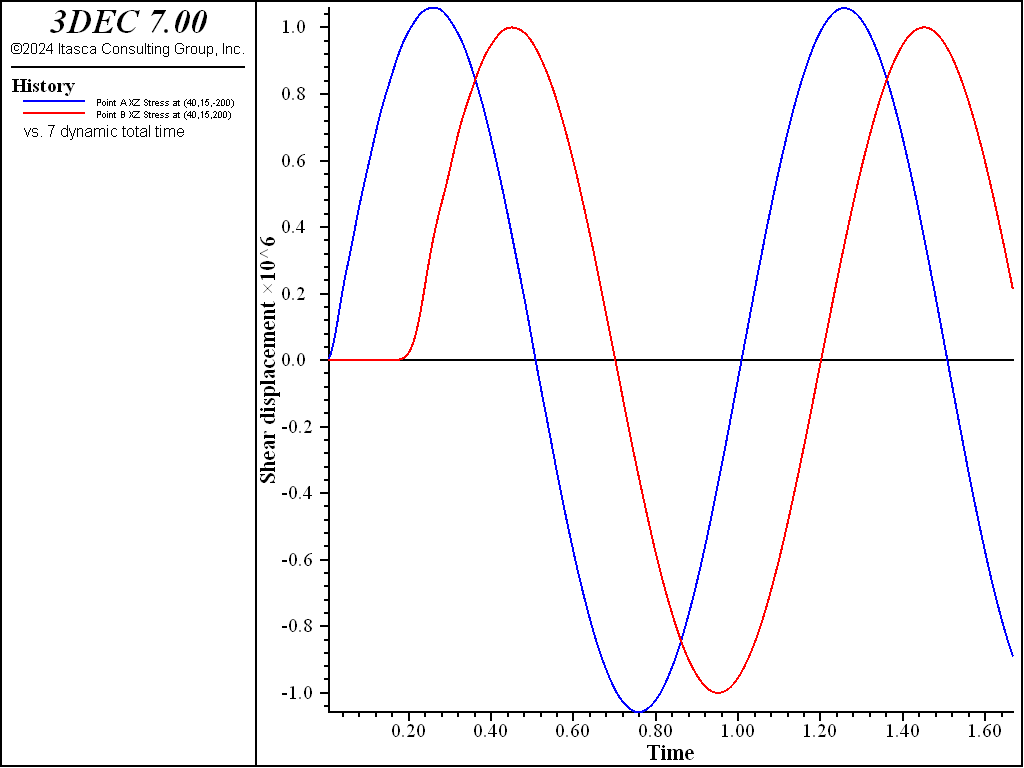
Figure 4: Shear stress vs time at Points A and B for the case of an elastic discontinuity (cohesion = 2.5 MPa).
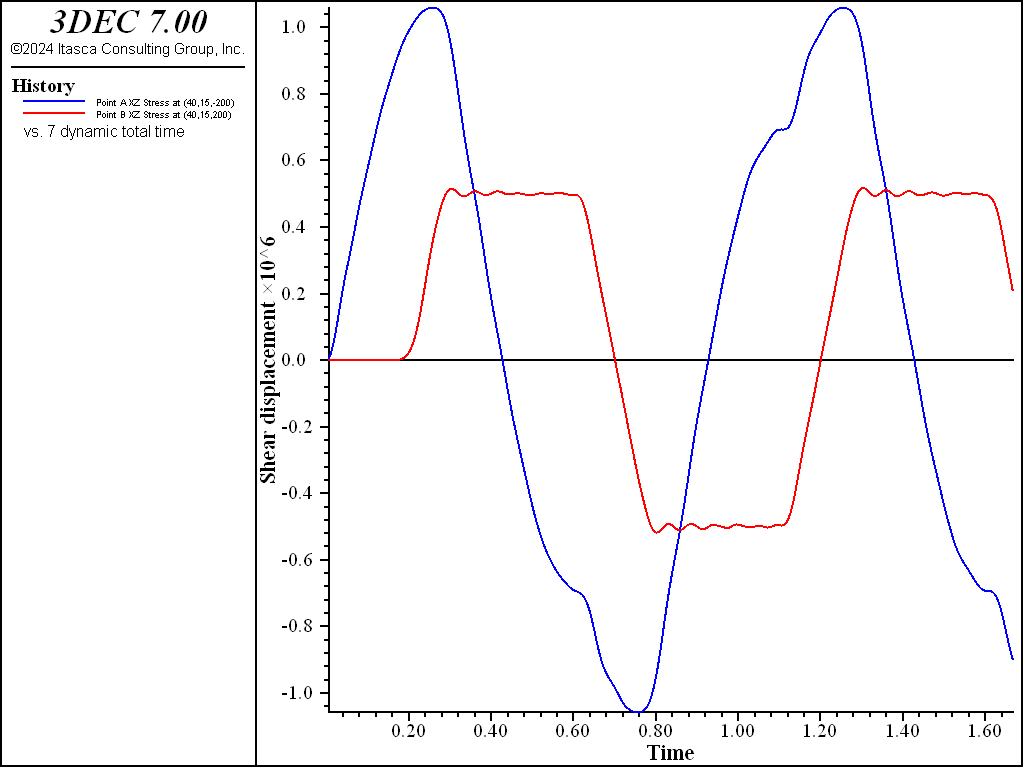
Figure 5: Shear stress vs time at Points A and B for the case of an elastic discontinuity (cohesion = 0.5 MPa).

Figure 6: Shear stress vs time at Points A and B for the case of an elastic discontinuity (cohesion = 0.1 MPa).
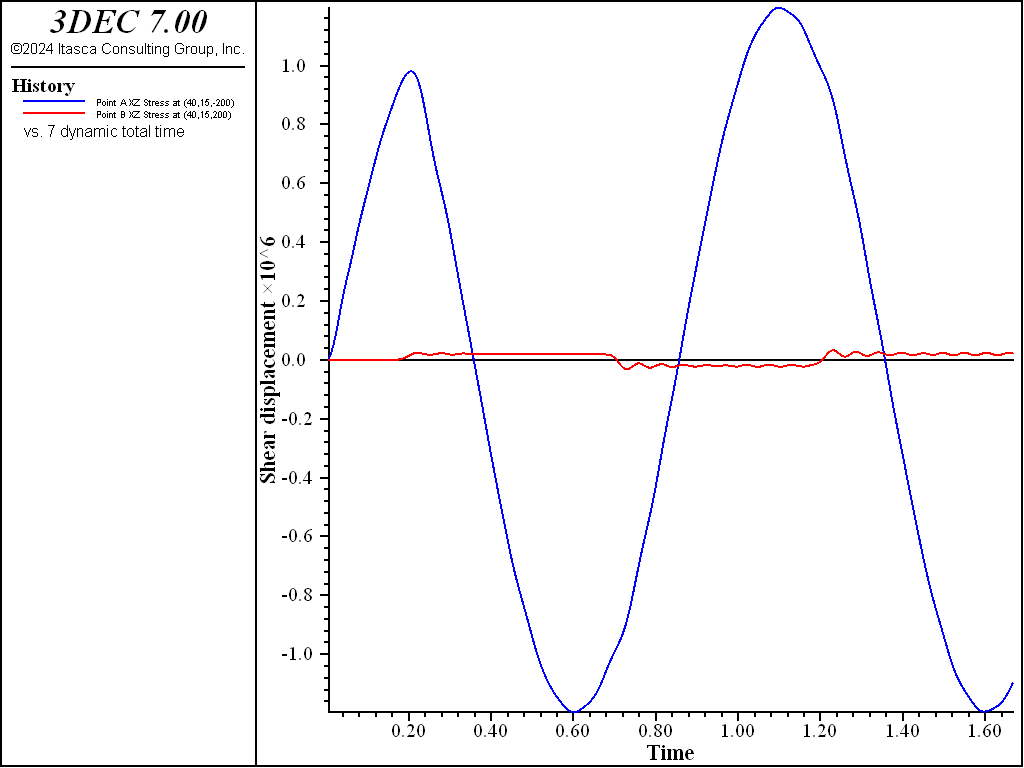
Figure 7: Shear stress vs time at Points A and B for the case of an elastic discontinuity (cohesion = 0.02 MPa).
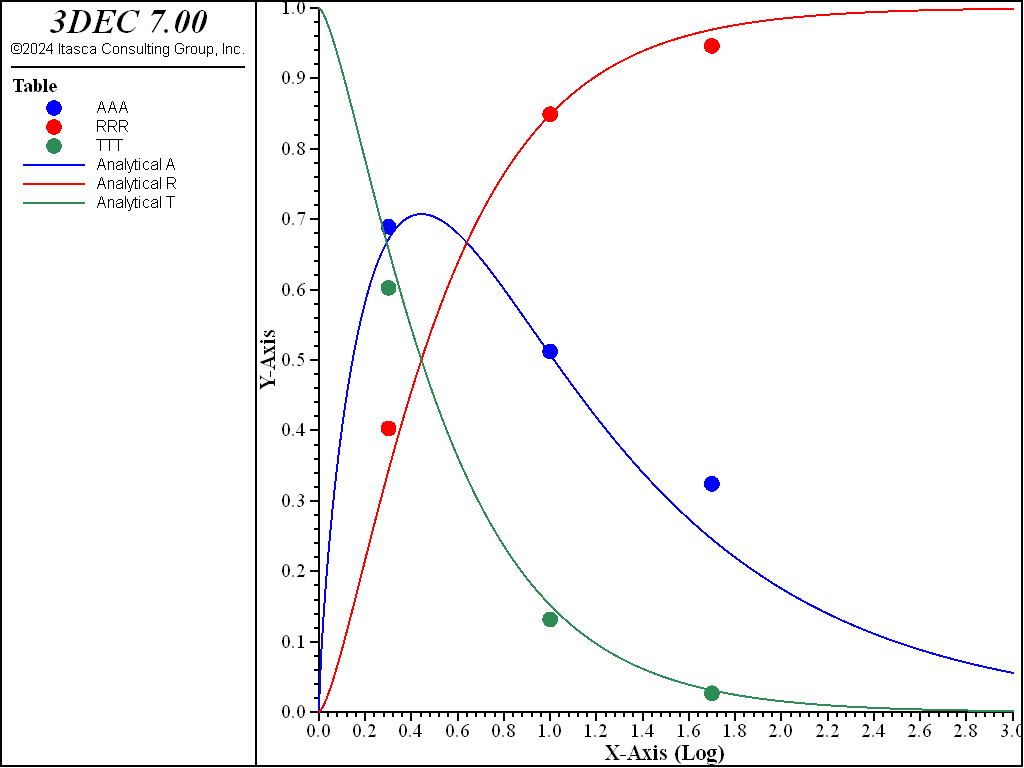
The energy flux, \(E_I\), is evaluated using Equation (2) at Point A for non-slipping discontinuities (i.e., cohesion = 2.5 MPa). \(E_T\) is evaluated at Point B for the slipping discontinuity (i.e., cohesion = 0.5, 0.1 and 0.02MPa). \(E_R\) is determined at PointB by taking the difference in velocity from the runs with slipping and non-slipping discontinuities. The coefficients of reflection (R), transmission (T ), and absorption (A) are computed using Equation (1) (see FISH function fenergy in file “sihsw.fis” below), and are plotted in Figure 8, along with the analytical solution (Miller 1978). The 3DEC results agree very well with the analytical solution (Figure 8).
Data File
;---------------------------------------------------------------------
; script file for dynamic problem 'Slip induced by harmonic wave'
;---------------------------------------------------------------------
model new
fish automatic-create off
model title "Slip induced by harmonic wave"
model config dyn
model large-strain on
fish define setup
global mat_shear = 1e10
global mat_dens = 2650
global freq = 1.0
global tload = 10.0
global w = 2.0 * math.pi * freq
global height = 400.0
end
[setup]
block create brick 0,80 0,30 -200,200
block cut joint-set dip-direction=90 dip 0 origin 80,0,0
;
block zone generate edgelength 31
;
block zone cmodel assign el
block zone prop dens=[mat_dens] bulk=16.667e9 shear=[mat_shear]
;
; set viscous boundary along xy plane at z=-200 and z=200
block gridpoint apply visc-x visc-z range pos-z -200
block gridpoint apply visc-x visc-z range pos-z 200
;
; set roller boundary along xz plane at y=0 and y=30
block gridpoint apply vel-y=0 range pos-y 0
block gridpoint apply vel-y=0 range pos-y 30
;
; set zvel=0 along yz plane at x=0 and x=80
block gridpoint apply vel-z=0 range pos-x 0
block gridpoint apply vel-z=0 range pos-x 80
;
; shear stress along xz plane at z=-200
; set sinusoidal wave function for the
; applied stress at the boundary
; freq = 1 Hz[freq = 10.0]
fish def sin_
sin_ = math.sin(2.0*math.pi*mech.time*freq)
end
block face apply stress-xz 2e6 fish sin_ range pos-z -200
; set histories
hist interval=10
block hist name 'Point A' stress-xz pos 40,15,-200
block hist name 'Point B' stress-xz pos 40,15,200
block hist name 'v1' vel-x pos (40,15,-200)
block hist name 'v2' vel-x pos (40,15,200)
block hist name 'd1' disp-x pos (40,15,-200)
block hist name 'd2' disp-x pos (40,15,200)
model hist name 'time' dynamic time-total
program call "sihsw.fis"
model save 'dint_ini'
; joint is elastic
block contact jmodel assign el
block contact prop stiffness-normal=10.0e9 stiffness-shear=10.0e9
block contact material-table default prop stiffness-normal=10.0e9 ...
stiffness-shear=10.0e9
model cyc 3000
history export 'v1' vs 'time' table '1'
table '1' export 'elastic' truncate
[find_u]
model save "dinte"
; ---cohesion 0.5 ---
model rest "dint_ini"
; joint is perfectly plastic
block contact jmodel assign mohr
block contact prop stiffness-normal=10.0e9 stiffness-shear=10.0e9 ...
coh=0.5e6 ten=1e12 coh-res 0.5e6 ten-res 1e12
block contact material-table default prop stiffness-normal=10.0e9 ...
stiffness-shear=10.0e9
model cyc 3000
table '1' import 'elastic'
history export 'v1' vs 'time' table '2'
history export 'v2' vs 'time' table '3'
[energy(0.5e6)]
; create and export tables for comparison with analytical solution
table '10' export 'AAA' truncate
table '11' export 'RRR' truncate
table '12' export 'TTT' truncate
model save "dint0p5"
; --- cohesion 0.1 ---
model rest "dint_ini"
block contact jmodel assign mohr
block contact prop stiffness-normal=10.0e9 stiffness-shear=10.0e9 ...
coh=0.1e6 ten=1e12 coh-res 0.1e6 ten-res 1e12
block contact material-table default prop stiffness-normal=10.0e9 ...
stiffness-shear=10.0e9
model cyc 3000
table '1' import 'elastic'
history export 'v1' vs 'time' table '2'
history export 'v2' vs 'time' table '3'
; import existing tables or results so new values are appended
table '10' import 'AAA'
table '11' import 'RRR'
table '12' import 'TTT'
[energy(0.1e6)]
; now export
table '10' export 'AAA' truncate
table '11' export 'RRR' truncate
table '12' export 'TTT' truncate
model save "dint0p1"
; --- cohesion 0.1 ---
model rest "dint_ini"
block contact jmodel assign mohr
block contact prop stiffness-normal=10.0e9 stiffness-shear=10.0e9 ...
coh=0.02e6 ten=1e12 coh-res 0.02e6 ten-res 1e12
block contact material-table default prop stiffness-normal=10.0e9 ...
stiffness-shear=10.0e9
model cyc 3000
table '1' import 'elastic'
history export 'v1' vs 'time' table '2'
history export 'v2' vs 'time' table '3'
table '10' import 'AAA'
table '11' import 'RRR'
table '12' import 'TTT'
[energy(0.02e6)]
table '10' export 'AAA' truncate
table '11' export 'RRR' truncate
table '12' export 'TTT' truncate
model save "dint0p02"
; --- get analytical solution ---
model new
table '10' import 'AAA'
table '11' import 'RRR'
table '12' import 'TTT'
table '10' label 'AAA'
table '11' label 'RRR'
table '12' label 'TTT'
program call "sihsw-ana.fis"
[analytical_table]
model save 'anal_tables'
Fish File
;--------------------------------------------------------------------------
; FISH functions for dynamic problem 'Slip induced by harmonic wave'
;---------------------------------------------------------------------------
fish def ini_time
global speed = math.sqrt(mat_shear/mat_dens)
global time0 = 0.0
global time1 = height/speed
global time2 = time1 + 1./freq
end
[ini_time]
fish define find_u
command
history export 'd1' vs 'time' table '4'
end_command
local pnt = table.get(4)
local s = table.size(pnt)
local max_disp = 0.0
local min_disp = 1e20
loop local i (1,s)
local time = table.x(pnt,i)
if time >= time1 then
if time <= time2 then
local val = math.abs(table.y(pnt,i))
max_disp = math.max(max_disp,val)
min_disp = math.min(min_disp,val)
end_if
end_if
end_loop
global UUU = (max_disp - min_disp) * 0.5
; write to file for use later
local status = file.open('ufile.txt',1,1)
local line = array.create(1)
line(1) = UUU
status = file.write(line,1)
status = file.close
end
fish define read_u
local status = file.open('ufile.txt',0,1)
local line = array.create(1)
file.read(line,1)
UUU = float(line(1))
end
fish define energy(cohesion) ;- compute energy coefficients
; for slipping-joint example -
; table 1 - x-velocity at point A for elastic joint case
; table 2 - x-velocity at point A for slipping joint case
; table 3 - x-velocity at point B for slipping joint case
; table 10 - A values for all cases
; table 11 - R values for all cases
; table 12 - T values for all cases
; Ei - energy flux for incident wave
; Et - energy flux for transmitted wave
; Er - energy flux for reflected wave
; AAA - a measure of energy absorbed at the interface
; Places AAA, RRR, TTT results in A, R, T tables
local Cs = math.sqrt(mat_shear / mat_dens)
local factor = mat_dens * Cs
local Ei = 0.0
local Et = 0.0
local Er = 0.0
local t_n_1 = 0.0
local AAA = 0.0
local TTT = 0.0
local RRR = 0.0
local items = table.size(1)
loop local i (1,items)
local t_n = table.x(1,i)
local d_t = t_n - t_n_1
t_n_1 = t_n
local Vsa_e = table.y(1,i)
local Vsa_s = table.y(2,i)
local Vsb_s = table.y(3,i)
Ei = Ei + factor * Vsa_e * Vsa_e * d_t
Et = Et + factor * Vsb_s * Vsb_s * d_t
Er = Er + factor * (Vsa_s-Vsa_e) * (Vsa_s-Vsa_e) * d_t
end_loop
RRR = math.sqrt(Er/Ei)
TTT = math.sqrt(Et/Ei)
AAA = AAA + math.sqrt(1.0-RRR*RRR-TTT*TTT)
; for analytical solution
read_u
local g = math.sqrt(mat_dens*mat_shear)
local x = (w * g * UUU) / cohesion
local aaatab = table.get(10)
table(aaatab,x) = AAA
local rrrtab = table.get(11)
table(rrrtab,x) = RRR
local ttttab = table.get(12)
table(ttttab,x) = TTT
end
Line Source in an Infinite Elastic Medium with a Discontinuity
Problem Statement
This problem concerns the dynamic behavior of a single discontinuity under explosive loading. The problem, shown in Figure 9, consists of a planar crack of infinite lateral extent in an elastic medium, and a dynamic load at some distance, \(h\), from the discontinuity. This problem was modeled using 3DEC to determine the dynamic response of the discontinuity for a line source (in the \(z\)-direction). The slip of the interface at a Point P, obtained by numerical analysis using 3DEC, is compared with the closed-form solution derived by Day (1985).
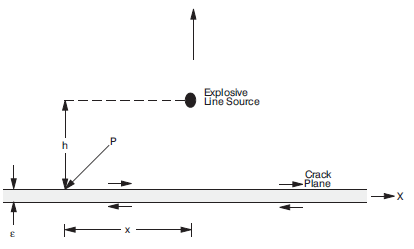
Figure 9: Problem geometry for an explosive source near a slip-prone discontinuity.
Analytic Solution
The closed-form solution for crack slip as a function of time was derived by Day (1985) and is given by
where
\(r\) = \((x^2 + h^2)^{1/2}\), distance from the point source to the point on the crack where the slip is monitored;
\(H(\tau)\) = step function;
\(\tau\) = \(t - (r/\alpha)\);
\(m_o\) = source strength;
\(\alpha\) = velocity of pressure wave;
\(\beta\) = velocity of shear wave;
\(\rho\) = density;
\(\eta_\alpha\) = \({(\alpha^{-2} - p^2)}^{1/2}, Re\ \eta_\alpha\ \ge\ 0\);
\(\eta_\beta\) = \({(\beta^{-2} - p^2)}^{1/2}, Re\ \eta_\beta \ \ge\ 0\);
\(R(p)\) = \({(1 - 2\beta^2\ p^2)}^2 + 4\beta^4\ \eta_\alpha\ \eta_\beta\ p^2 + 2\beta\ \eta_\beta\ \gamma\); and
\(p~\) = \({{1} \over {r^2}} \biggl[ \ \bigl(\tau + {{r} \over {\alpha}}\bigr)x + i\bigl(\tau + {{2r} \over {\alpha}}\bigr)^{1/2}\ \tau^{1/2}\ h\ \biggr]\).
The slip response of the discontinuity for any source history, \(S(t)\), can be obtained by convolution of Figure 9 and the source function, \(S(t)\):
Figure 10 shows the dimensionless analytical results of slip history at a Point P for a smooth step function, and for the following values of the variables: \(\alpha^2 = 3\beta^2\), \(h = x\) and \(\gamma = 0\). The analytic solution is implemented in FISH function fana slp (listed below).
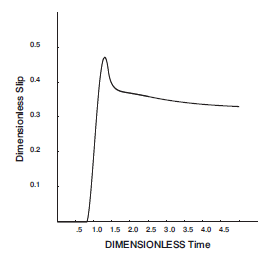
Figure 10: Dimensionless analytical results of slip history at Point P (dimensionless slip = \((4h \rho \beta^2/m_o)\delta u\), dimensionless time = \(t\beta / h\)) (Day 1985).
Model Setup
Figure 11 shows the problem geometry modeled by 3DEC. The source is located at A (\(x\) = 0 and \(z\) = 2 \(h\)), and the discontinuity is located at \(z = h\). The dynamic input was applied at the semicircular boundary of radius 0.05 h. The slip movement was monitored at Point P on the discontinuity.
The continuous medium was modeled with elastic, fully deformable blocks, as shown in Figure 12, and each block was further discretized into tetrahedral zones. In order to generate only one zone in the \(y\)-direction, the thickness of the block in the \(y\)-direction and the average edge length of the tetrahedron were assumed to be the same. The average edge length was 0.065 \(h\). All of the joints except the discontinuity were “joined” in order to model a continuous elastic medium. The discontinuity was assigned a high normal stiffness and high tensile strength in order to meet the assumption implied in the analytical solution.
Nonreflecting boundary conditions were applied along the horizontal boundaries at the top and bottom of the model and along the vertical boundary at \(x\) = 4 \(h\). A symmetric boundary condition was applied along the vertical boundary at \(x\) = 0. In order to simulate plane-strain conditions, displacement in the \(y\)-direction is restrained along \(xz\)-planes at \(y\) = 0 and \(y\) = 0.065 \(h\).
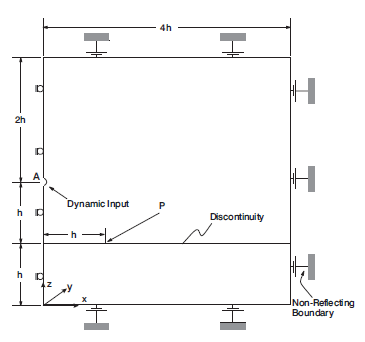
Figure 11: Problem geometry and boundary conditions for numerical model.
Properties of Joints and Continuous Medium
The following properties were used for the elastic blocks.
| Geometric scale | \(h\) = 10, 000 MPa/m |
| Mass density density | 10,000 MPa/m |
| Shear modulus shear | 100 Pa |
| Bulk modulus bulk | 166.67 Pa |
The Mohr-Coulomb joint constitutive relation was used in the analysis. The specific 3DEC parameters used for the joint relation are listed below.
| Normal stiffness stiffness-normal | 10,000 Pa/m |
| Shear stiffness stiffness-shear | 0.1 Pa/m |
| Friction angle friction | 0 |
| Cohesion cohesion | 0 |
Dynamic Loading
Radial velocities corresponding to the dynamic solution for a line source in an infinite medium were enforced at the semicircular boundary. To avoid problems with the singularity at the source, dynamic input was applied over a surface 0.05 \(h\) from the nominal point source.
3DEC analysis with both velocity and pressure input showed that velocity input gives a better match with the analytical solution than pressure input. The velocity boundary provides a more accurate representation of the dynamic stress than the pressure boundary, because in pressure input, the source function is simply scaled by static stress magnitude and neglects the inertial effects of dynamic stress at the input boundary.
The radial displacement for a line source given by Lemos (1987) is
where \(r\) is the radial distance.
The corresponding velocity is
The actual input velocity record at \(r = 0.05 h\), as shown in Figure 13, was obtained by convoluting Equation (4) and Equation (3).
Figure 13: Input radial velocity time history prescribed at \(r = 0.05\ h\) (dimensionless velocity = \((h^2\rho\beta / m_o)v\), dimensionless time = \(\tau\beta/ h)\).
Velocity history at the boundary at \(r = 0.05 h\) is calculated in the FISH function fvel inp (listed below).
Results
The dimensionless slip at Point P is plotted against the dimensionless time, and is shown in Figure 14. The dimensionless slip is compared with the analytical solution given by Day (1985). Velocity input was used on the semicircular region at \(r = 0.05 h\) for 3DEC. The error at the peak slip for 3DEC is 1.7%.
The results shown in Figure 14 were obtained with a mesh of maximum zone length of 0.065 \(h\). The slip response on the discontinuity involves higher frequency components because of zero friction along the discontinuity. This requires a finer mesh for accurate representation.
The dimensionless slip in Figure 14 for 3DEC analysis shows a good agreement with the analytical solution until the dimensionless time of 1.49. The results show, after dimensionless time of 1.49, a considerable deviation, which can be attributed to boundary reflections.
Nonreflecting boundaries are used along the top, bottom, and right-hand side boundaries. Such viscous boundaries, designed to absorb normally incident \(p-\) and \(s\)-waves, cannot be fully effective in this dynamic slip problem because the discontinuity crosses the boundary. Viscous boundaries, however, are preferable to roller boundaries.
Figure 14: Comparison of dimensionless slip at Point P with Coulomb joint model (dimensionless slip = \((4h\rho\beta^2/ m_o)\delta u\), dimensionless time = \(\tau\beta/h\)).
Data File - Line Source
;==========================================================================
; verification test -- 3dec modeling of slipping crack under dynamic load
; Joint Model: Mohr-Coulomb Model
; elastic blocks
;
; dynamic analysis
;==========================================================================
;
model new
model random 10000
model config dynamic
model large-strain on
; --- geometry ---
block create brick 0,40 0,0.65 0,40
;
block cut j-set dip 0 d-d 0 ori 0,0,10
block hide range pos-x 0,40 pos-y 0,10 pos-z 0,10
block cut j-set dip 45 d-d 90 ori 0,0,25 join
block hide range plane dip 45 d-d 90 ori 0,0,25 above
block cut j-set dip 45 d-d 270 ori 0,0,15 join
;
block hide off
block cut tunnel ...
face-1 0,0,20.5 0.19,0,20.46 .35,0,20.35 0.46,0,20.2 .5,0,20.0 ...
.46,0,19.8 0.35,0,19.64 .19,0,19.53 0.0,0,19.5 ...
face-2 0,.65,20.5 0.19,.65,20.46 .35,.65,20.35 0.46,.65,20.2 .5,.65,20.0 ...
.46,.65,19.8 0.35,.65,19.64 .19,.65,19.53 0.0,.65,19.5 ...
group 'tunnel'
;
block delete range group 'tunnel'
block zone gen edgelength 0.650
model save "day3d-zoned"
model rest "day3d-zoned"
; --- properties ---
block zone cmodel assign el
block zone prop dens=1.0 bulk=166.67 shear=100.0
block contact jmodel assign mohr
block contact prop stiffness-normal 1e4 stiffness-shear 0.1 ten 1e6
block contact material-table default prop stiffness-normal 1e4 ...
stiffness-shear 0.1
;
; --- boundary conditions
block gridpoint apply visc-x visc-z range pos-z 0 ; xz plane at z=0
block gridpoint apply visc-x visc-z range pos-z 40 ; xz plane at z=40
block gridpoint apply visc-x visc-z range pos-x 40 ; xz plane at x=40
;
; set roller boundary along xz plane at y=0 and y=0.65
block gridpoint apply vel-y=0 range pos-y 0.0
block gridpoint apply vel-y=0 range pos-y 0.65
; set symm boundary at x=0
block gridpoint apply vel-x=0 range pos-x -1 .5
; set velocity boundary condition along cylindrical notch
program call "vel_inp.fis"
program call "ana_slp.fis"
model cycle 1
program call "day3d.fis"
[_load( 0.0, 20.0, 0.5)]
;
block insitu stress -1.0e-9 -1.0e-9 -1.0e-9 0 0 0
; set histories
hist interval=10
fish hist dtime_
fish hist name 'Input Velocity' bvel_
fish hist name 'Analytical Solution' aslip_
fish hist name '3DEC Solution' nslip1_
fish hist nslip2_
block hist vel-x pos 0.5 20 0.3
block hist vel-z pos 0 20.5 .03
block hist vel-z pos 0 19.5 0.03
model hist dynamic time-total
fish callback add _compare 1
model cyc 4000
model save "day3d"
Fish File
;=====================================================
;
; calculates unit forces on the contour of the opening
;
;=====================================================
;
fish def _load(xc_, zc_, dist_)
loop foreach igp_ block.gp.list
x_ = block.gp.pos.x(igp_)
z_ = block.gp.pos.z(igp_)
d_ = math.sqrt((x_-xc_)*(x_-xc_)+(z_-zc_)*(z_-zc_))
if math.abs(d_-dist_) < 0.05*dist_
nx_ = (x_-xc_)/d_
nz_ = (z_-zc_)/d_
gp_id = block.gp.id(igp_)
command
block gridpoint apply vel-x [nx_] vel-z [nz_] ...
table [_vtab] range id [gp_id]
end_command
end_if
end_loop
end
;=====================================================
;
; finds contacts closest to the point of interest
; input 2 vectors
;
;=====================================================
fish def _find(f_, b_)
global v_s_
global h_n_
global rho_
global m0_
dfmax_ = 1.e30
dbmax_ = 1.e30
loop foreach icx_ block.subcontact.list
pos_ = block.subcontact.pos(icx_)
df_= math.mag(pos_ - f_)
db_= math.mag(pos_ - b_)
if df_ < dfmax_ then
dfmax_ = df_
icf_ = icx_
end_if
if db_ < dbmax_ then
dbmax_ = db_
icb_ = icx_
end_if
end_loop
vscale_ = m0_/(h_n_*h_n_*rho_*v_s_)
dscale_ = 0.25*m0_/(h_n_*rho_*v_s_*v_s_)
end
[v_s_=10.]
[h_n_=10.]
[rho_=1.]
[m0_=1.]
[_find( (10,10,0), (10,10,0.65) )]
;=====================================================
;
; stores analytical solution in the histories, and
; convertes numerical solution in the dimensionless
; form
;
;=====================================================
[nslip1_max = 0.0]
[aslip_max = 0.0]
fish def _compare
;while_stepping
dtime_ = dynamic.time.total*v_s_/h_n_
bvel_ = table(_vtab,dynamic.time.total)/vscale_
aslip_ = table(_utab,dtime_)
slip1_ = block.subcontact.disp.shear(icf_)
slip2_ = block.subcontact.disp.shear(icb_)
nslip1_ = math.mag(slip1_)/dscale_
nslip2_ = math.mag(slip2_)/dscale_
nslip1_max = math.max(nslip1_max,nslip1_)
aslip_max = math.max(aslip_max,aslip_)
end
Fish File - Velocity Input
;=====================================================
;
; Fish function for generating the radial velocity
; input profile at r=0.05h
;
; Input:
; vl --- P-wave velocity
; per --- period of wave
; tt --- total time
; xd --- horizontal distance
; nt --- total number of dat points
;
; Output:
; velocity profile stored in table 1
;=====================================================
;
fish def ini_par
vl = 0.0
per = 0.0
tt = 0.0
xd = 0.0
nt = 1000
_vtab = '1' ; table storing velocity profile
_fptab = '2'
_vhtab = '3'
end
[ini_par]
;
fish def vel_inp
if xd <= 0.0
exit
endif
if per <= 0.0
exit
endif
_w = 2.0*math.pi/per
_dt = tt/float(nt)
_ca = -1./(2.0*math.pi*vl)
_cb = _ca/(xd * xd)
_cc = _cb * _dt
;
; Obtain velocity record by performing convolution
; using the radial displacement for a step function
; and second derivative of the pressure history
;
loop _n (1, nt)
_t = float(_n-1) * _dt
table.x(_fptab, _n) = _t
if _t < 0.5*per
table.y(_fptab, _n) = 0.5*_w*_w*math.cos(_w*_t)
_nfp = _n
else
table.y(_fptab, _n) = 0.0
endif
end_loop
;
; --- displacement -----
;
_t0 = xd/vl
_j0 = int(_t0/_dt)
_j0 = _j0 + 1
loop _n (1, nt)
_t = float(_n-1) * _dt
if _n < _j0
table.y(_vhtab, _n) = 0.0
else
_t = _t0 + 0.5*_dt + float(_n-_j0)*_dt
_cf = _t*vl/xd
_cf2 = _cf * _cf
_cs = math.sqrt(_cf2 - 1.0)
_cg = _cs / _t
table.y(_vhtab, _n) = _cc / _cg
endif
table.x(_vhtab, _n) = _t
end_loop
;
; ---- velocity ---------
;
table.y(_vtab, 1) = 0.0
table.x(_vtab, 1) = 0.0
loop _n (2, nt)
_vn = 0.0
_j1 = math.min(_nfp, _n-1)
loop _n1 (1, _j1)
_vn = _vn + table.y(_fptab, _n1) * table.y(_vhtab, (_n - _n1))
end_loop
table.y(_vtab, _n) = _vn
end_loop
;
; Change sign for pressures source
;
_vmax = -1e20
_vmin = 1e20
loop _n (1, nt)
table.y(_vtab, _n) = -1.0*table.y(_vtab, _n)
_vi = table.y(_vtab, _n)
vmin = math.min(_vmin, _vi)
vmax = math.max(_vmax, _vi)
table.x(_vtab, _n) = float(_n-1)*_dt
end_loop
; oo = io.out(' vmin, vmax = ', string(vmin), ',', string(vmax))
end
[vl=17.32]
[per=1.2]
[tt=1.4]
[xd=0.5]
[nt=1000]
tab [_vtab] add 0,0
tab [_fptab] add 0,0
tab [_vhtab] add 0,0
[vel_inp]
Fish File - Analytical Solution
;=====================================================================
; This function evaluates the dynamic response of the slip of a
; single discontinuity of infinite extent caused by an explosive
; loading. Analytical solution of a line source in an elastic medium
; with a discontinuity is given by S. M. Day (1985).
;
; Input: _nt --- total number of data points to be created
; _dt --- time increment
; _xd --- horizontal distance, x
; _hd --- vertical distance, _hd
; per --- period of input function
; rho --- density
; m0 --- source strength
; gamma --- dimensionless bonding parameter
; _vp --- velocity of pressure wave
; _vs --- velocity of shear wave
;
; Output: Dimensionless relation stored in table 4.
; Non-normalized values are stored in table 6.
;=====================================================================
;
fish def add_complex(Re_a, Im_a, Re_b, Im_b)
; Summation of two complex variables
; Input : Za, Zb
; Output: Z = Re(Z) + Im(Z)
Re_z = Re_a + Re_b
Im_z = Im_a + Im_b
end
;
fish def mult_complex(Re_a, Im_a, Re_b, Im_b)
; multiplication of two complex variables
; Input : Za, Zb
; Output: Z = Re(Z) + Im(Z)
Re_z = Re_a*Re_b - Im_a*Im_b
Im_z = Re_a*Im_b + Im_a*Re_b
end
;
fish def divi_complex(Re_a, Im_a, Re_b, Im_b)
; division of complex variables Za/Zb
_deno = Re_b * Re_b + Im_b * Im_b
if _deno = 0.0
divi_compex = 1
exit
endif
Re_z = (Re_a*Re_b + Im_a*Im_b)/_deno
Im_z = (Im_a*Re_b - Re_a*Im_b)/_deno
end
;
fish def sqrt_complex(Re_x, Im_x)
; squart root of a complex variable
; Input : Zx
; Output: Zr = Re(Zr) + Im(Zr)
; _theta = atan2(Im_x, Re_x) * 0.5
_arg = float(Im_x/Re_x)
_theta = math.atan(_arg) * 0.5
_sqrtr = math.sqrt(math.sqrt(Re_x*Re_x + Im_x*Im_x))
Re_zr = _sqrtr*math.cos(_theta)
Im_zr = _sqrtr*math.sin(_theta)
end
;
fish def ana_slp
;
; Input _nt, _dt, _xd, _hd, gamma, per, rho
;
global _nt
global _dt
global _xd
global _hd
global gamma
global per
global rho
global _vs
global _vp
global m0
global _utab
global _ftab
global _uftab
_dt = float(_dt)
_xd = float(_xd)
_hd = float(_hd)
gamma = float(gamma)
per = float(per)
rho = float(rho)
;
_vs2 = _vs*_vs
_vs4 = _vs2*_vs2
_2vs2 = 2.0 * _vs2
_4vs4 = 4.0 * _vs4
_r = math.sqrt(_xd*_xd + _hd*_hd)
_r2 = _r * _r
loop _n (1, _nt)
_t = float(_n) * _dt
_tau = _t - _r/_vp
if _tau > 0.0
_t2r2 = math.sqrt(_t*_t - (_r/_vp)*(_r/_vp))
Re_cp = _t*_xd / _r2
Im_cp = _t2r2*_hd / _r2
Re_a = Re_cp
Im_a = Im_cp
Re_b = Re_cp
Im_b = Im_cp
mult_complex(Re_a,im_a,Re_b,im_b) ; Z^ 2 ---> Re(Z) + Im(Z)
Re_z2 = Re_z
Im_z2 = Im_z
;
Re_x = 1.0/(_vp*_vp) - Re_z2
Im_x = -1.0 * Im_z2
sqrt_complex(Re_x,Im_x) ; sqrt(Zx)
Re_cetap = Re_zr
Im_cetap = Im_zr
;
Re_x = 1.0/(_vs*_vs) - Re_z2
Im_x = -1.0 * Im_z2
sqrt_complex(Re_x,Im_x) ; sqrt(Zx)
Re_cetas = Re_zr
Im_cetas = Im_zr
;
Re_a = 1.0 - _2vs2 * Re_z2
Im_a = -1.0 * _2vs2 * Im_z2
Re_b = Re_a
Im_b = Im_a
mult_complex(Re_a,Im_a,Re_b,Im_b) ; (1. - 2.*vs^ 2*cp^ 2) ^ 2
Re_temp1 = Re_z
Im_temp1 = Im_z
;
Re_a = Re_cetap
Im_a = Im_cetap
Re_b = Re_cetas
Im_b = Im_cetas
mult_complex(Re_a,Im_a,Re_b,Im_b) ; cetap * cetas
Re_a = Re_z
Im_a = Im_z
Re_b = Re_z2
Im_b = Im_z2
mult_complex(Re_a,Im_a,Re_b,Im_b) ; cetap * cetas * cp^ 2
Re_temp2 = _4vs4 * Re_z
Im_temp2 = _4vs4 * Im_z
;
Re_cr = Re_temp1 + Re_temp2
Im_cr = Im_temp1 + Im_temp2
Re_cr = Re_cr + 2.0 * _vs * gamma * Re_cetas
Im_cr = Im_cr + 2.0 * _vs * gamma * Im_cetas
_dut = 2.0*m0*_vs*_vs/(math.pi*rho*_vp*_vp)
; note Re_a, Im_a store (cetap*cetas)
Re_b = Re_cp
Im_b = Im_cp
mult_complex(Re_a,Im_a,Re_b,Im_b) ; cetap * cetas * cp
;
Re_a = Re_z
Im_a = Im_z
Re_b = Re_cr
Im_b = Im_cr
if divi_complex(Re_a,Im_a,Re_b,Im_b) = 1 ; cetap * cetas * cp / cr
oo = io.out(' divided by zero')
exit
endif
_dut = _dut * Re_z / _t2r2
table.y(_utab, _n) = _dut
else
table.y(_utab, _n) = 0.0
endif
end_loop
;
_nf = int(per/_dt + 0.0001)
_sum = 0.0
loop _n (1, _nf)
_ph = float(_n) * _dt / per
if _ph < 1.0
table.y(_ftab, _n) = math.sin(math.pi * _ph)
else
table.y(_ftab, _n) = 0.0
endif
_sum = _sum + table.y(_ftab, _n)
end_loop
;
; du vs. time relation
;
loop _i (1, _nt)
_uf = 0.0
_n = math.min(_nf, _i)
loop _j (1, _n)
_uf = _uf + table.y(_utab,_i-_j+1)*table.y(_ftab,_j)
end_loop
table.y(_uftab, _i) = _uf / _sum
table.x(_uftab, _i) = float(_i) * _dt
end_loop
;
; Dimensionless relation
;
loop _n (1, _nt)
table.y(_utab, _n) = (4.0*_hd*rho*_vs*_vs/m0)*table.y(_uftab, _n)
table.x(_utab, _n) = float(_n) * _dt * _vs / _hd
end_loop
;
end
[_nt=1000]
[_dt = 0.005]
[_xd=10.]
[_hd=10.]
[_vs=10.]
[_vp=17.320508]
[gamma=0.0]
[per=0.6]
[rho=1.0]
[m0=1.0]
[_utab='4']
[_ftab='5']
[_uftab='6']
;
tab [_utab] add 0,0
tab [_ftab] add 0,0
tab [_uftab] add 0,0
[ana_slp]
References
Bathe, K.-J., and E. L.Wilson. Numerical Methods in Finite Element Analysis. Englewood Cliffs, New Jersey: Prentice-Hall Inc. (1976).
Belytschko, T. “An Overview of Semidiscretization and Time Integration Procedures,” in Computational Methods for Transient Analysis, Ch. 1, pp. 1-65. New York: Elsevier Science Publishers, B.V. (1983).
Biggs, J. M. Introduction to Structural Dynamics. New York: McGraw-Hill (1964).
Chopra, A. K. Dynamics of Structures. Prentice Hall (1995).
Cundall, P. A. “Adaptive Density-Scaling for Time-Explicit Calculations,” in Proceedings of the 4th International Conference on Numerical Methods in Geomechanics (Edmonton, Canada, 1982), pp. 23-26 (1982).
Cundall, P. A., et al. “Computer Modeling of Jointed Rock Masses,” U.S. Army, Engineer Waterways Experiment Station, Technical Report WES-TR-N-78-4 (August 1978).
Cundall, P. A., et al. “NESSI – Soil Structure Interaction Program for Dynamic and Static Problems,” Norwegian Geotechnical Institute, Report 51508-9 (December 1980).
Cundall, P. A., et al. “Solution of Infinite Domain Dynamic Problems by Finite Modelling in the Time Domain,” in Proceedings of the 2nd International Conference on Applied Numerical Modelling (Madrid, Spain, September 1978), pp. 341-351. London: Pentech Press (1979).
Day, S. M. “Test Problem for Plane Strain Block Motion Codes,” S-Cubed Memorandum (May 1 1985).
Ferreira, A. J. M., and G. E. Fasshauer. “Computation of natural frequencies of shear deformable beams and plates by an RBF-pseudospectral method,” Comput. Methods Appl. Mech. Engrg., 196, 134-146 (2006).
Gemant, A., and W. Jackson. “The Measurement of Internal Friction in Some Solid Dielectric Materials,” The London, Edinburgh, and Dublin Philosophical Magazine & Journal of Science, XXII, 960-983 (1937).
Gerrard, C. M. “Elastic Models of Rock Masses Having One, Two and Three Sets of Joints,” Int. J. Rock Mech. Min. Sci. & Geomech. Abstr., 19, 15-23 (1982).
Kuhlmeyer, R. L., and J. Lysmer. “Finite Element Method Accuracy for Wave Propagation Problems,” J. Soil Mech. & Foundations Div., ASCE, 99(SM5), 421-427 (May, 1973).
Kunar, R. R., P. J. Beresford and P. A. Cundall. “A Tested Soil-Structure Model for Surface Structures,” in Proceedings of the Symposium on Soil-Structure Interaction (Roorkee University, India, January 1977), Vol. 1, pp. 137-144. Meerut, India: Sarita Prakashan (1977).
Lemos, J. “A Distinct Element Model for Dynamic Analysis of Jointed Rock with Application to Dam Foundations and Fault Motion.” Ph.D. Thesis, University of Minnesota (June 1987).
Lemos, J. “Numerical Issues in the Representation of Masonry Structural Dynamics with Discrete Elements,” in Proceedings of the ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (Rethymno, Crete, Greece, 13-16 June 2007). M. Papadrakakis et al., eds. (2007).
Lysmer, J., and R. Kuhlemeyer. “Finite Dynamic Model for Infinite Media,” J. Eng. Mech., Div. ASCE, 95:EM4, 859-877 (1969).
Lysmer, J., and G. Waas. “Shear Waves in Plane Infinite Structures,” J. Eng. Mech., Div. ASCE, 98, 85-105 (1972).
Miller, R. K. “The Effects of Boundary Friction on the Propagation of Elastic Waves,” Bull. Seis. Soc. America, 68, 987-998 (1978).
Myer, L. R., L. J. Pyrak-Nolte and N. G. W. Cook. “Effects of Single Fractures on Seismic Wave Propagation,” in Proceedings of the International Symposium on Rock Joints, pp. 413-422. Rotterdam: A. A. Balkema (1990).
Ohnishi, Y., et al. “Verification of Input Parameters for Distinct Element Analysis of Jointed Rock Mass,” in Proceedings of the International Symposium on Fundamentals of Rock Joints (Björkliden, Sweden, September 1985), pp. 205-214. O. Stephansson, ed. Luleå: CENTEK Publishers (1985).
Otter, J. R. H., A. C. Cassell and R. E. Hobbs. “Dynamic Relaxation,” Proc. Inst. Civil Eng., 35, 633-665 (1966).
Roesset, J. M., and M. M. Ettouney. “Transmitting Boundaries: A Comparison,” Int. J. Num. & Analy. Methods Geomech., 1, 151-176 (1977).
Seed, H. B., P. P. Martin and J. Lysmer. “The Generation and Dissipation of Pore Water Pressures during Soil Liquefaction,” University of California, Berkeley, Earthquake Engineering Research Center, NSF Report PB-252 648 (August 1975).
Singh, B. “Continuum Characterization of Jointed Rock Masses: Part I – The Constitutive Equations,” Int. J. Rock Mech. Min. Sci. & Geomech. Abstr., 10, 311-335 (1973).
Wegel, R. L., and H.Walther. “Internal Dissipation in Solids for Small Cyclic Strains,” Physics, 6, 141-157 (1935).
White, W., S. Valliappan and I. K. Lee. “Unified Boundary for Finite Dynamic Models,” J. Eng. Mech., Div. ASCE, 103, 949-964 (1977).
Wolf, J. P. Dynamic Soil-Structure Interaction. New Jersey: Prentice-Hall (1985).
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |