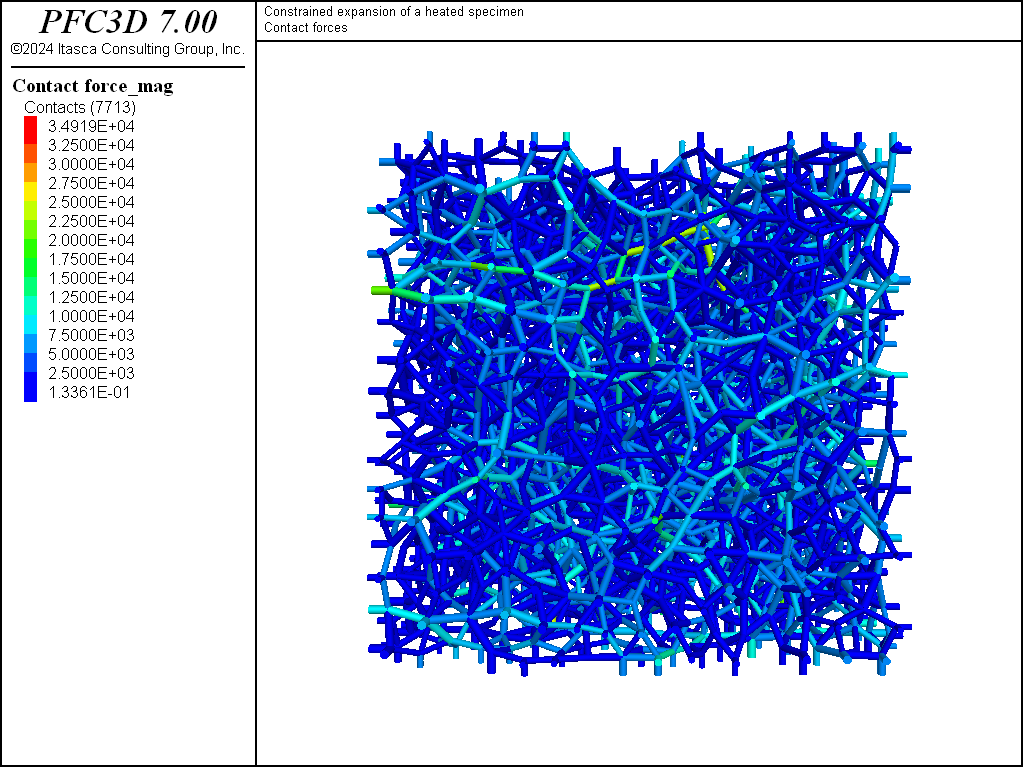
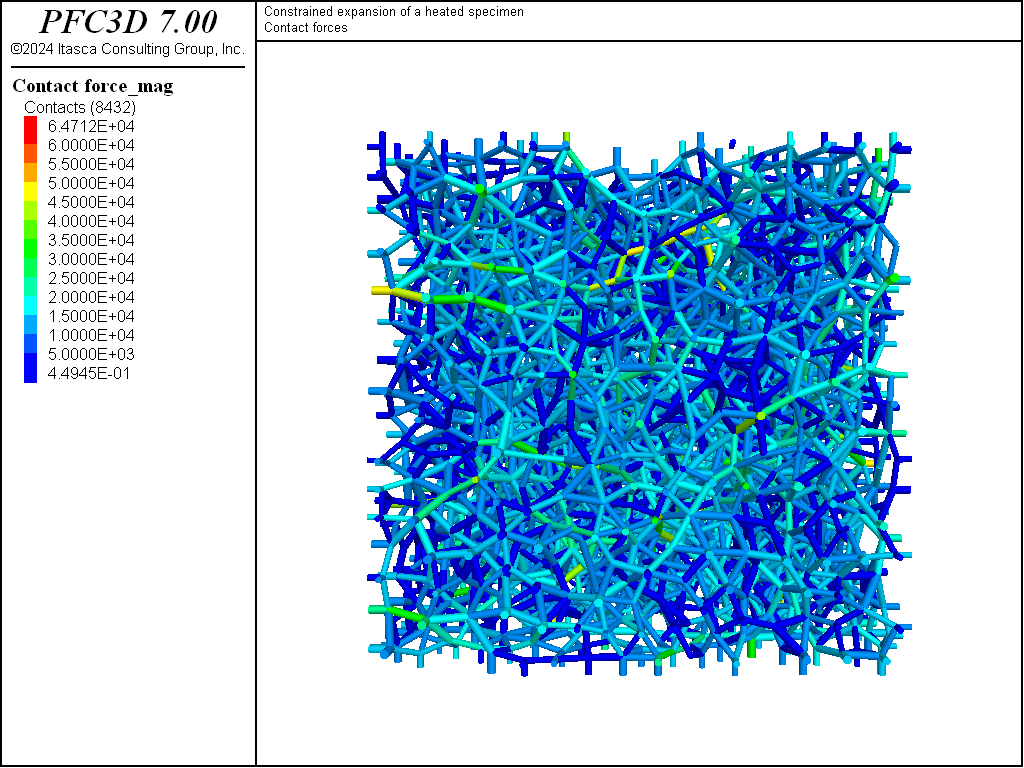
Heated Specimen with Fixed Boundaries

Note

The project file for this example may be viewed/run in PFC.[1] The data files used are shown at the end of this example.

A temperature increment, \(\Delta T\), is applied to a cubic specimen with constrained boundaries. The surrounding six walls are fixed to constrain the expansion of the specimen, and thermally induced stresses are measured and compared with the analytical values.

Analytical Values

The stress-strain relation with thermally induced strain is given by Equation (1) ([Timoshenko1970a]):

(1)\[\begin{split}\epsilon_x &= {1 \over E} {\big[ \sigma_x - \nu (\sigma_y+\sigma_z) \big]} + \alpha_t \Delta T \\ \epsilon_y &= {1 \over E} {\big[ \sigma_y - \nu (\sigma_z+\sigma_x) \big]} + \alpha_t \Delta T \\ \epsilon_z &= {1 \over E} {\big[ \sigma_z - \nu (\sigma_x+\sigma_y) \big]} + \alpha_t \Delta T\end{split}\]

where \(E\) and \(\nu\) are the Young’s modulus and the Poisson’s ratio, respectively. Also, \(\alpha_t\) is the coefficient of linear thermal expansion.

The analytical values for thermally induced stresses on the isotropic specimen are given by Equation (2), substituting \(\sigma_x=\sigma_y=\sigma_z\) and \(\epsilon_x=\epsilon_y=\epsilon_z=0\) into Equation (1):

(2)\[\sigma_x = \sigma_y = \sigma_z = -\alpha_t \Delta T {E \over {1-2\nu}}\]

Model and Results

The file “constrained_expansion.dat” is used for this example. A 2 × 2 × 2 m specimen is created. It comprises approximately 4000 balls with uniform size distribution (radius range from 0.05 to 0.08 m) and a porosity of 0.38. Once the specimen is generated and equilibrated under an isotropic stress state of 100kPa, contact bonds are installed at ball-ball contacts.

The stress and strains are measured using a measurement sphere with a radius of 0.95 m centered within the specimen, and the stresses are also measured on the boundary walls. In PFC, the particle thermal-expansion coefficient is the same as the coefficient of linear thermal expansion: \(\alpha_t\) = 3 × 10^-6/°C in this case.

The increment of stress measured at the boundary walls during thermal isotropic constrained expansion are:

(3)\[\begin{split}\Delta \sigma_xx &= -2.98 \times 10^5 \\ \Delta \sigma_yy &= -2.95 \times 10^5 \\ \Delta \sigma_zz &= -3.04 \times 10^5\end{split}\]

Figures 1 and 2 shows the contact forces colored by magnitude before and after thermal expansion.

Figure 1: Contact forces before thermal isotropic constrained expansion.

Figure 2: Contact forces after thermal isotropic constrained expansion.

To evaluate the analytical solution, the Young’s modulus, \(E\), and the Poisson’s ratio, \(\nu\), are computed by a confined compression test of the specimen at a lateral confinement 100 kPa.

(4)\[\begin{split}E &= 366 \ {\rm MPa} \\ \\ \nu &= 0.314\end{split}\]

Incorporating these values into Equation (2) leads to:

(5)\[\sigma_x = \sigma_y = - 2.95 \times 10^5\]

This value compares well with the measured stress increments reported in (3). The difference may be attributed to the fact that the specimen is not completely uniform; the arbitrary packing produces heterogeneity in the material microstructure.

Reference

[Timoshenko1970a]

Timoshenko, S. P., and J. N. Goodier. Theory of Elasticity, 3rd Ed. New York: McGraw-Hill, 1970.

Data Files

constrained_expansion.dat

; fname: constrained_expansion.dat (3D)
;
; Itasca Consulting Group, Inc.
; ========================================================================
; Thermal option verification problem:
;        Constrained expansion of a heated specimen
;
; ========================================================================
program log-file 'constrained_expansion.log'
program log on
; ========================================================================
model new
model large-strain on
model title 'Constrained expansion of a heated specimen'

; -------------------- build specimen ------------------------------------
model domain extent -5 5
contact cmat default  model linearcbond    ...
              method deformability emod 3.0e9 kratio 1.0
              
wall generate box -1 1
model random 10001
ball distribute resolution 1.0    ...
                porosity 0.38     ...
                radius 0.05 0.08  ...
                box -1 1

ball attribute density 2500.0 damp 0.7
model cycle 2000 calm 100
model mechanical timestep scale
model solve

ball property 'fric' 0.5
ball attribute displacement multiply 0.0 
model cycle 1000
model mechanical timestep auto
model solve

model save 'initial'

; --------------- apply isotropic stress ---------------------------------
model restore 'initial'
program echo off
  program call 'triaxial_utils.p3fis'
program echo on

; expand walls 
[expand_walls(1.25)]

; install measurement sphere and activate strain calculation
measure create id 1 radius 0.95
[ini_measure]
fish callback add accumulate_mstrains 11.0 

; activate wall servo-control
[tsa = -1.0e5]
[tsl = -1.0e5]
[do_zservo = true]
fish callback add servo_walls 1.0

[tol =  5e-3]
[gain_cnt = 0]
[gain_update_freq = 100]
[gain_safety_fac = 0.1]
fish define stop_me
    gain_cnt = gain_cnt + 1
    if gain_cnt >= gain_update_freq then
        compute_gain(gain_safety_fac)
        gain_cnt = 0
    endif
    if math.abs((swxx - tsl)/tsl) > tol
        exit
    endif
    if math.abs((swyy- tsl)/tsl) > tol
        exit
    endif
    if math.abs((swzz - tsa)/tsa) > tol
        exit
    endif
    if mech.solve("ratio-average") > 1e-4
        exit
    endif
    stop_me = 1
end

[wlx0 = wlx] 
[wly0 = wly]
[wlz0 = wlz]
[swxx0 = swxx] 
[swyy0 = swyy]
[swzz0 = swzz]
[smxx0 = smxx] 
[smyy0 = smyy]
[smzz0 = smzz]

fish history emxx
fish history emyy
fish history emzz
fish history ewxx
fish history ewyy
fish history ewzz
fish history  smxx
fish history  smyy
fish history  smzz
fish history  swxx
fish history  swyy
fish history  swzz
model history name "100" mechanical ratio-average 

[compute_gain(0.1)]
model solve fish-halt stop_me

; bond active ball-ball contacts
contact method bond gap 0.0 range contact type "ball-ball"
contact property cb_tenf 1e20 cb_shearf 1e20 range contact type "ball-ball"
model save 'iso'

;-------------- estimate Young Modulus and Poisson ratio -----------------
model restore 'iso'
model calm
ball attribute displacement multiply 0.0 
[do_zservo = false]
[wlx0 = wlx] 
[wly0 = wly]
[wlz0 = wlz]
wall attribute vel-z  0.0001 range id 1
wall attribute vel-z -0.0001 range id 2


[gain_cnt = 0]
[compute_gain(0.5)]
[gain_safety_fac = 0.5]
fish define stop_me2
  gain_cnt = gain_cnt + 1
  if gain_cnt >= gain_update_freq then
    compute_gain(gain_safety_fac)
    gain_cnt = 0
  endif
  if ewzz <= -1e-4 then
    stop_me2 = 1
  endif
end

[ini_measure]
[smxx0 = smxx] 
[smyy0 = smyy]
[smzz0 = smzz]
[swxx0 = swxx] 
[swyy0 = swyy]
[swzz0 = swzz]
history delete
;set display fish ewzz
model solve fish-halt stop_me2

fish define compute_deformability
  local  stress = measure.stress(mp)  
  global ymodm  = (smzz - smzz0) / emzz 
  global pratm  = - 0.5*(emxx + emyy) / emzz
  ;
  global ymodw  =  (swzz - swzz0) / ewzz 
  global pratw  = - 0.5*(ewxx + ewyy) / ewzz
  
end
[compute_deformability]
model save 'aniso'

;---------------- fix walls and apply +100 deg C -------------------------
model restore 'iso'
fish callback remove servo_walls 1.0
model calm
ball attribute displacement multiply 0.0
wall attribute velocity multiply 0.0
[ini_measure]
[swxx0 = swxx] 
[swyy0 = swyy]
[swzz0 = swzz]
[smxx0 = smxx] 
[smyy0 = smyy]
[smzz0 = smzz]

history delete
model configure thermal
ball thermal attribute expansion 3.0e-6
ball thermal attribute specific-heat 1.0e3
ball thermal attribute temperature 0.0
ball thermal attribute temperature-increment=100.0
model cycle 1
model thermal off mechanical on
model cycle 1000
model solve

fish define compute_dsig
  global dsmxx = smxx - smxx0 
  global dsmyy = smyy - smyy0 
  global dsmzz = smzz - smzz0 
  global dswxx = swxx - swxx0 
  global dswyy = swyy - swyy0 
  global dswzz = swzz - swzz0 
end
[compute_dsig]

model save 'final'

program log off
program return
; ========================================================================
; eof: constrained_expansion.dat (3D)

Endnotes

[1]	To view this project in PFC, use the program menu. Help ▼ Examples…   ⮡   PFC     ⮡   Thermal       ⮡   ConstrainedExpansion         ⮡   ConstrainedExpansion.prj