WIPP-Salt Model: Hydrostatic Compression Test

Note

To view this project in 3DEC, use the menu command Help ► Examples…. Choose “CreepMaterialModels/ CompressionCrushedSalt” and select “CompressionCrushedSalt.prj” to load. The project’s main data files are shown at the end of this example.

Results of the hydrostatic compression test are presented here to validate the WIPP-Salt model in 3DEC. The test involves one zone at an initially elastic state of equilibrium. The zone is allowed to creep for a period of 23 days, during which time the fractional density is monitored and compared to the analytical calculation.

In this hydrostatic compression test, the confining pressure is held constant. The rate of change of density (see WIPP-Salt model) is

(1)\[\dot{\rho} = B_0 \left[e^{-B_1 \sigma} - 1 \right] e^{B_2 \rho}\]

Note that \(B_0 \left[e^{-B_1 \sigma} - 1 \right]\) is constant for this problem.

Using definition \(F_d = \rho / \rho_f\) (see WIPP-Salt model) for the fractional density, and given that \(\rho = \rho_{\circ}\) at \(t\) = 0, integration of Equation (1) yields

(2)\[F_d = - {{1}\over{B_2 \rho_f}} ln \biggl[-B_2 B_0 \left[e^{-B_1 \sigma} - 1 \right]t + e^{-B_2 \rho_{\circ}} \biggr]\]

where \(\rho_f\) is the density of intact salt.

Also, integrating \(\dot{\epsilon}_v = -\dot{\rho}/\rho\) (see WIPP-Salt model), we obtain, for zero initial strain,

(3)\[\epsilon_v = - ln {{\rho}\over{\rho_{\circ}}}\]

Numerical results for fractional density versus creep time are compared to the analytical calculations in Figure 1 for a stress level of 8.97 MPa. The initial density is 1350 kg/m³, and the final density is 2300 kg/m³.

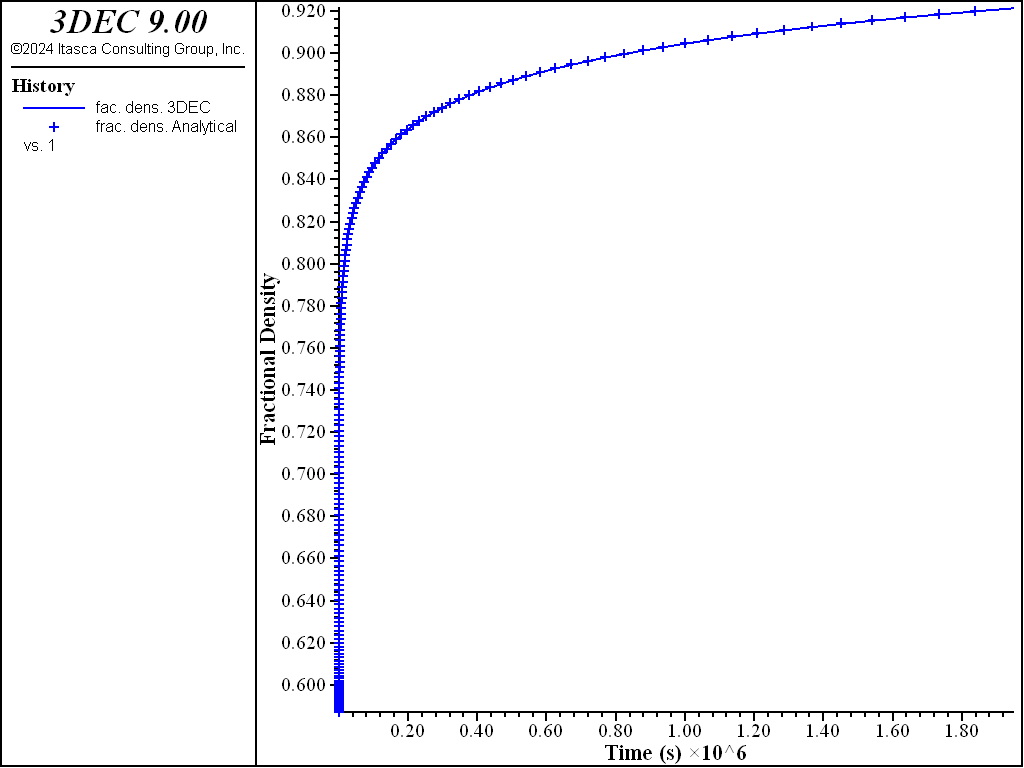
Figure 1: Comparison of numerical and analytical prediction for fractional density.

Data File

CompressionCrushedSalt.dat

model new
; File: CompressionCrushedSalt.dat
; Hydrostatic compression of crushed salt
; --- constants ---
fish define cons
   global valsig = -8.97e6
   global valb0  = 1.3e8
   global valb1  = 0.82e-6
   global valb2  = -1.72e-2
   global valrho = 1350.
   global valrhof= 2300.
   global valbf  = 58.6383e9
   global valsf  = 35.3163e9
   global valterm = valb0 * (math.exp(-valb1*valsig)-1.)
   global valcons = math.exp(-valb2*valrho)
end
[cons]
;
; --- geometry ---
model configure creep
model large-strain off
block create brick 0 5 0 5 0 5
block zone generate hexahedra 
block zone cmodel assign wipp-salt
block zone property bulk 1.186E8 shear 7.14E7 young 1.784E8 poisson 0.2493 ...
  activation-energy 1.2E4 constant-a 4.56 constant-b 127 constant-d 5.79E-36 ...
  creep-rate-critical 5.39E-8 constant-gas 1.987 exponent 4.9 temperature 300 ...
  density [valrho] bulk-final [valbf] shear-final [valsf] density-final [valrhof] ...
  compaction-0 [valb0] compaction-1 [valb1] compaction-2 [valb2] density-salt [valrho]
;
program call 'solution.fis'

; --- histories ---
history interval 100
model history creep time-total
model history timestep
fish history name 'fac. dens. 3DEC' c_frd
fish history name 'frac. dens. Analytical' c_frdsol
fish history name 'error' c_err
fish history c_ev
fish history c_evsol
fish history c_rbulk
block history displacement-x position 5 0 0
block history displacement-x position 5 5 5
block history displacement-z position 0 0 5
block history displacement-z position 5 0 5
;
model creep timestep starting 5.e-7
model creep timestep minimum 5.e-7
model creep timestep maximum 5e4
model creep timestep lower-multiplier 1.001
model creep timestep automatic
;
block face apply stress [valsig] 0.0 0.0 0 0 0 range position-x 5
block face apply stress 0.0 [valsig] 0.0 0 0 0 range position-y 5
block face apply stress 0.0 0.0 [valsig] 0 0 0 range position-z 5
block gridpoint apply velocity-x 0 range position-x 0
block gridpoint apply velocity-y 0 range position-y 0
block gridpoint apply velocity-z 0 range position-z 0

; --- initial conditions ---
block insitu stress [valsig] [valsig] [valsig] 0 0 0

model solve time-total 2e6
;
model save 'crushed_salt'
;
;