Excavation in a Saturated Soil
Problem Statement
Note
The project file for this example may be viewed/run in 3DEC.[1] The data files used are shown at the end of this example.
An excavation is planned in a saturated soil layer resting on an impervious base. The soil layer has a thickness of 12 m. The level of the phreatic surface is constant and corresponds to the soil top-surface. The excavation will have a square cross-section of dimensions 8 m × 8 m, and a depth of 5 m. In preparation for this work, the excavation site has been surrounded by vertical impervious walls 1 m thick which extend 2 m below the excavation bottom. After excavation, pumps are installed to lower the water level to the excavation bottom. The problem is to assess the total upheave at the excavation bottom resulting from excavation and drainage.
The problem is three-dimensional but, by symmetry, a quarter of the domain may be considered in the analysis. A system of coordinate axes is defined with the origin at the center of the excavation in the plane of the soil surface, and the \(z\)-axis pointing downward. In this example, boundaries at \(|x|\) = 12 m and \(|y|\) = 12 m are viewed as planes of symmetry. Figure 1 provides a sketch of the problem conditions.
The soil is considered as an elastic material. The soil and water have several properties:
bulk modulus, \(K\): 390 MPa
shear modulus, \(G\): 280 MPa
soil dry density, \(\rho_d\): 1200 kg/m3
water density, \(\rho_w\): 1000 kg/m3
wall density, \(\rho_{wall}\): 1500 kg/m3
permeability, \(k\): 10−12 m2/Pa-s
porosity, \(n\): 0.3
fluid bulk modulus, \(K_f\): 2.0 GPa
The modulus \(g\) of the gravity vector may be approximated as 10 m/s2. The initial state corresponds to a state of equilibrium (after installation of the walls), in which the horizontal isotropic stresses are such that \({\sigma'}_{xx} = {\sigma'}_{yy} = 0.4{\sigma'}_{zz}\).
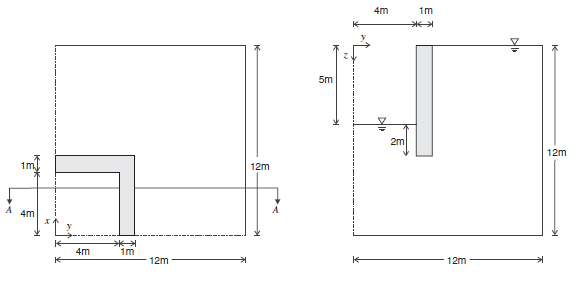
Figure 1: Excavation — quarter-section.
Modeling Procedure
The 3DEC model has the dimensions 12 m × 12 m × 12 m; the grid is made up of 0.5 m zones around the excavation and 1 m zones further away. (See Figure 2 for a plot of the grid.)
Note that, in this problem, the value \(\rho_d + n \rho_w\) for the saturated density of soil is equal to the wall density. Hence, the initial state is characterized by the uniform pore-pressure distribution \(p = \rho_w g z\) and the vertical stress distribution \({\sigma}_{zz} = -(\rho_d + n \rho_w) g z\). The horizontal stresses are found to be \({\sigma}_{xx}={\sigma}_{yy}=-[0.4 \rho_d + (0.4(n-1)+1) \rho_w] g z\). Those stresses are applied at the excavation walls to model the initial undisturbed stage.

Figure 2: 3DEC model.
As an illustration of the modeling procedure for a staged excavation, the analysis is divided into three stages. In the first stage, applied stresses at the excavation walls are changed to the isotropic value \({\sigma}_{xx}=\sigma_{yy}=\sigma_{zz}=- \rho_w g z\), corresponding to the water pressure in the undrained excavation. The pore pressure is fixed at the excavation bottom and at the soil surface. Flow of water is prevented using the command model fluid active off. The model is cycled to equilibrium to simulate a rapid (undrained) excavation process in the fluid-flow time scale.
In the second stage, the pressures are removed from the excavation walls, and flow of water is again disallowed. The model is cycled to model the effect of rapid lowering of the water table inside the excavation.
In the third stage, the pore pressure is fixed at the value zero at the excavation bottom, flow of water is allowed and the model is cycled further. The pore pressure is monitored at a point located 1 m below the excavation center (number 2 in Figure 2) to detect when steady-state flow conditions are reached. No effort is made to represent the true time scale of consolidation effects; we are simply interested in the final steady state.
The model contains 1728 zones and requires 140 MB of RAM. The data file for this problem, “excav.dat”, is listed in below.
Results
The pore-pressure contours at the end of each of the three stages are shown in Figure 3, 4, and 5.
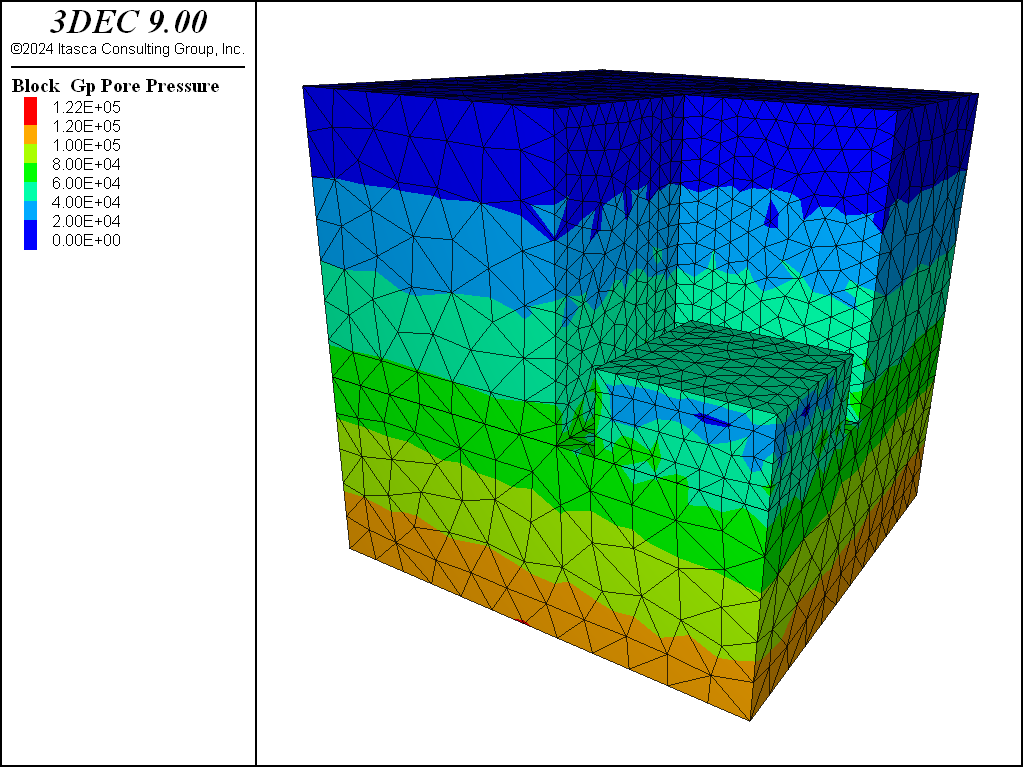
Figure 3: Pore-pressure contours after undrained excavation.
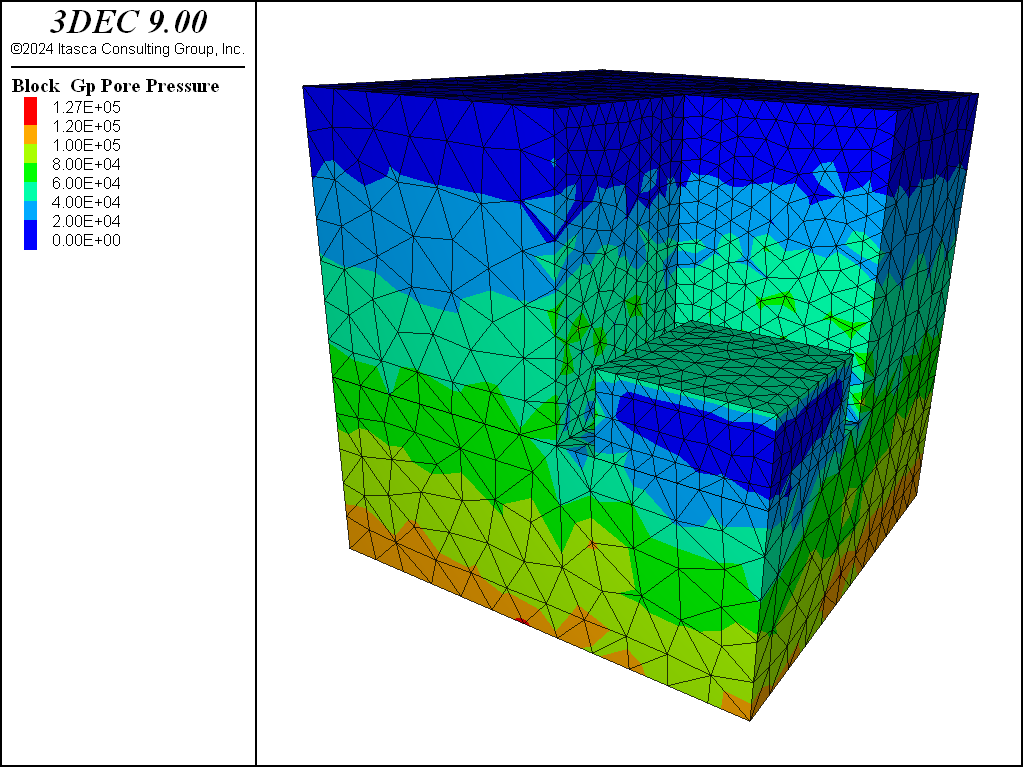
Figure 4: Pore-pressure contours after rapid drainage of the excavation.
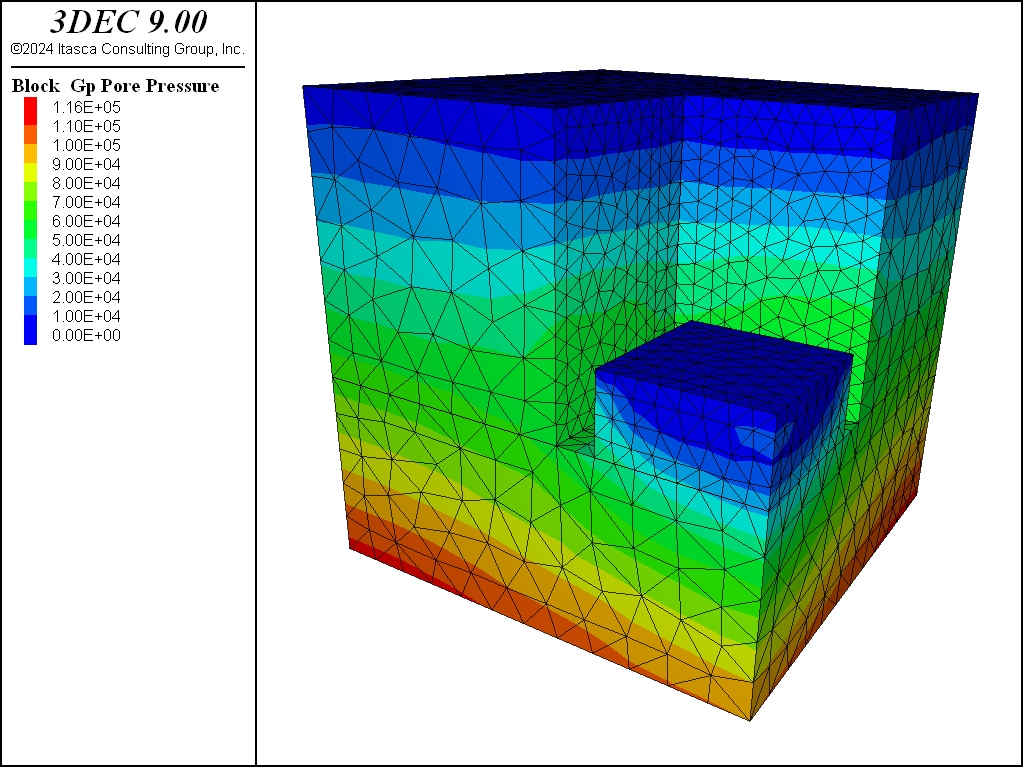
Figure 5: Pore-pressure contours after groundwater flow reaches steady state.
Histories of the vertical displacement at three points (numbers 6, 7, and 9 in Figure 2) located at the excavation base are taken. Results are presented in Figure 6. Heave at the excavation base is shown to occur during the first and second stages. This is caused by the removal of soil and drainage of water inside the excavation. During the third stage, a slight settlement occurs at the base as a result of groundwater flow into the region.
The steady-state flow of groundwater into the excavation at the third stage is shown by the flow vector plot in Figure 7.
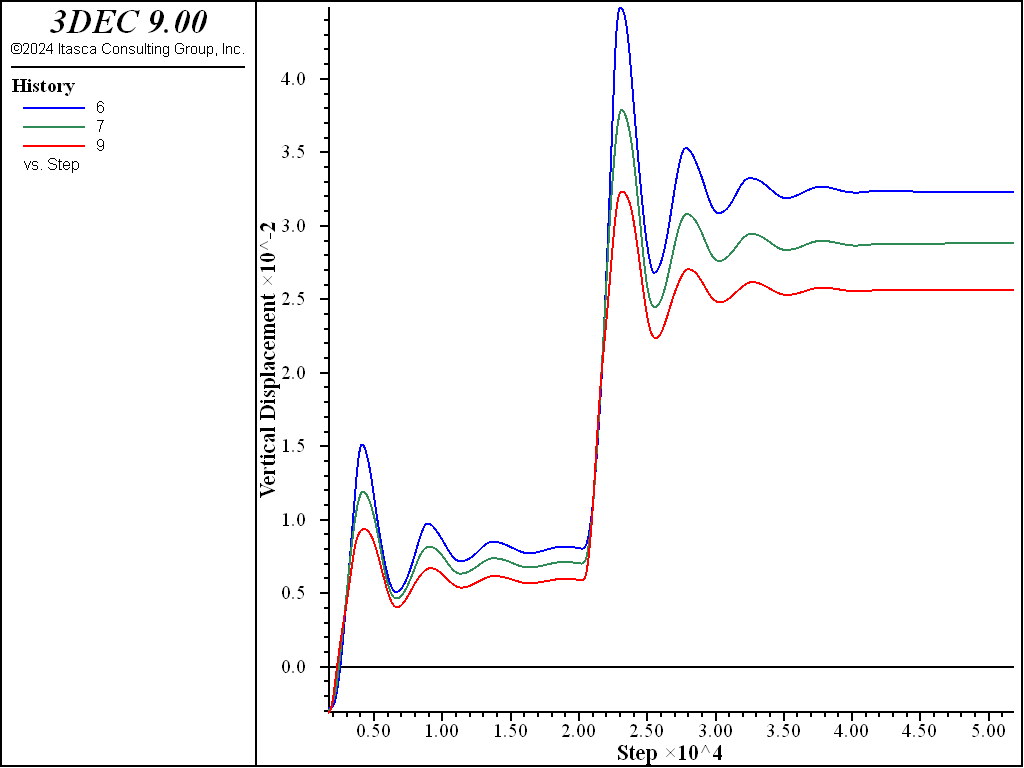
Figure 6: Vertical displacement histories at three points in the excavation base.
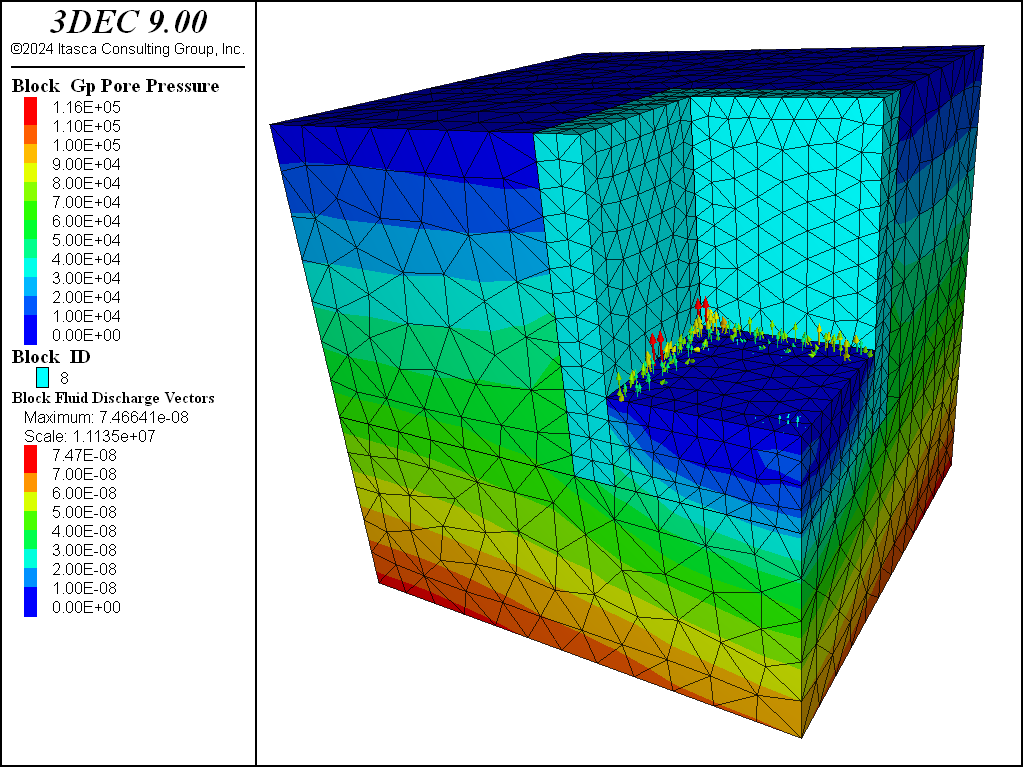
Figure 7: Steady-state fluid flow into the excavation.
Data File
excav.dat
program log on
program log-file 'excav.log'
;------------------------------------------------------
; Excavation in a saturated soil
;------------------------------------------------------
model new
fish automatic-create off
model title 'Excavation in a saturated soil'
;
model configure matrixflow
model large-strain off
;
; --- geometrical model ---
block create brick 0 12 0 12 -12 -7
block create brick 0 4 0 4 -7 -5
block create brick 5 12 0 5 -7 0
block create brick 0 5 5 12 -7 0
block create brick 5 12 5 12 -7 0
block group 'soil'
block hide
block create brick 4 5 0 4 -7 0
block create brick 0 4 4 5 -7 0
block create brick 4 5 4 5 -7 0
block group 'wall'
block hide off
;
block join
;
block zone generate edgelength 0.5 ...
range position-x 0 5 position-y 0 5 position-z -7 0
block zone generate edgelength 1
;
; --- properties ---
block zone cmodel assign elastic
block zone property density 1.5e3 bulk 3.9e6 shear 2.8e6
;
block fluid property density 1.0e3
; zero bulk modulus forigin initial balance stage
block fluid property bulk 1e-6
;
block zone fluid property porosity 0.3 range group 'soil'
block zone fluid property porosity 0.0 range group 'wall'
block zone fluid property permeability 1e-12 range group 'soil'
block zone fluid property permeability 0.0 range group 'wall'
;
; --- initial conditions
block insitu stress 0 0 0 0 0 0 gradient-z 1.2e4 1.2e4 1.5e4 0 0 0
block insitu pore-pressure 0 gradient 0 0 -1.0e4
;
; remove pressure inside wall blocks
block insitu pore-pressure 0.0 ...
range position-x -0.1 4.9 position-y 3.9 4.9 position-z -4.9 0.1
block insitu pore-pressure 0.0 ...
range position-x 3.9 4.9 position-y -0.1 4.9 position-z -4.9 0.1
;
; --- boundary conditions
block face apply stress 0 0 0 0 0 0 gradient-z 1.2e4 1.2e4 1.5e4 0 0 0 ...
range position-x -0.1 4.1 position-y -0.1 4.1 position-z -5
;
block gridpoint apply velocity-x 0.0 range position-x 0
block gridpoint apply velocity-x 0.0 range position-x 12
block gridpoint apply velocity-y 0.0 range position-y 0
block gridpoint apply velocity-y 0.0 range position-y 12
block gridpoint apply velocity-z 0.0 range position-z -12
;
flowknot apply pore-pressure 0.0 range position-z 0
flowknot apply pore-pressure 0.0 gradient -1.0e4 ...
range position-x -0.1 4.1 position-y -0.1 4.1 position-z -5
;
; --- settings ---
;
model gravity 0 0 -10.0
;
model fluid active off
;
block history displacement-x position 4 0 0
block history displacement-z position 4 0 0
;
; --- initial state ---
model solve
model cycle 1000
model save 'excav-0'
block list maxima
=========================================
;
history delete
model mechanical time-total 0
;
; --- histories ---
history interval 10
model history fluid time-total
flowknot history pore-pressure position 0 0 -6
block history displacement-x position 4 0 0
block history displacement-x position 4 0 -2
block history displacement-x position 4 2 0
block history displacement-z position 0 0 -5
block history displacement-z position 2 0 -5
block history displacement-z position 4 0 -5
block history displacement-z position 2 2 -5
block history displacement-z position 4 2 -5
block history displacement-z position 4 4 -5
block history displacement-z position 10 0 -1
block history displacement-z position 10 0 -2
flowknot history pore-pressure position 0 1 -6
flowknot history pore-pressure position 0 2 -6
flowknot history pore-pressure position 0 3 -6
flowknot history pore-pressure position 1 0 -6
flowknot history pore-pressure position 1 1 -6
flowknot history pore-pressure position 1 2 -6
flowknot history pore-pressure position 1 3 -6
;
; --- excavation ---
model fluid active off
; set real bulk modulus
block fluid property bulk 2.0e9
;
; remove effective stresses; leave pp load
block face apply stress 0 0 0 0 0 0 gradient-z -0.2e4 -0.2e4 -0.5e4 0 0 0 ...
range position-x -0.1 4.1 position-y -0.1 4.1 position-z -5.1 0.1
block gridpoint apply velocity-x 0.0 range position-x 0
block gridpoint apply velocity-x 0.0 range position-x 12
block gridpoint apply velocity-y 0.0 range position-y 0
block gridpoint apply velocity-y 0.0 range position-y 12
block gridpoint apply velocity-z 0.0 range position-z -12
;
model solve
model save 'excav-1'
block list maxima
===================================================
;
; --- drainage ---
fish define relaxsetup
global step0 = global.step
global ncycle = 1000
end
[relaxsetup]
;
fish define relax
global relax
local rstep = global.step - step0
if rstep < ncycle then
relax = 1.0 - (float(rstep)/float(ncycle))
else
relax = 0.0
endif
end
;
; remove pp load in 1000 steps
block face apply-remove stress ...
range position-x -0.1 4.1 position-y -0.1 4.1 position-z -5.1 0.1
block face apply stress 0 0 0 0 0 0 gradient-z 1.0e4 1.0e4 1.0e4 0 0 0 ...
fish relax ...
range position-x -0.1 4.1 position-y -0.1 4.1 position-z -5.1 0.1
block gridpoint apply velocity-x 0.0 range position-x 0
block gridpoint apply velocity-x 0.0 range position-x 12
block gridpoint apply velocity-y 0.0 range position-y 0
block gridpoint apply velocity-y 0.0 range position-y 12
block gridpoint apply velocity-z 0.0 range position-z -12
model cycle [ncycle]
model solve
model save 'excav-2'
block list maxima
========================================
;
; --- percolation ---
model fluid active on
model mechanical follower on
model mechanical substep 1
flowknot apply pore-pressure 0 ...
range position-x -0.1 4.1 position-y -0.1 4.1 position-z -5.1 0.1
;
model cycle 10000
model save 'excav-3'
block list maxima
;
;
Endnote
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Nov 12, 2025 |
