UCS Test with Voronoi Blocks

Problem Description

Note

The project file for this example may be viewed/run in 3DEC.[1] The data files used are shown at the end of this example.

This example describes how to perform an unconfined compression test on a cylindrical sample made up of bonded Voronoi blocks.

3DEC Model

The model is created by first importing a simple DXF of a parallelepiped. The shape is 6x6x12.5 cm. A voronoi assembly of blocks is then generated using the block generate voronoi command with the from-geometry keyword. A maximum edge length of 6 mm is specified, resulting in 3361 Voronoi blocks.

The model is then cut into a cylinder by importing a dxf of a cylinder and using the command block cut geometry. This step is necessary because the Voronoi blocks along the edges of the parallelepiped exhibit unrealistic alignment, leading to increased strength resulting from the “crystalline” packing. By cutting away the edges, this alignment is disrupted.

The blocks are then zoned and the resulting 3DEC model is shown in Figure 1.

../../../../_images/ucs-voro-sample.png

Figure 1: Blocks making up the model.

The zones are assumed to be elastic with a Young’s modulus of 76 GPa and a Poisson’s ratio of 0.25. The properties were chosen to mimic the numerical experiments described in Lan et al (2013). The contacts between the blocks were also assigned properties from Lan et al (2013) as shown in the following properties:

Table 1: Joint Properties

Property

value

Normal stiffness

7.6e4 GPa/m

Shear stiffness

7.6e4 GPa/m

Cohesion

40 MPa

Friction

10 degrees

Tension

14.4 MPa

The block is loaded by applying a constant velocity of 0.05 m/s to the gridpoints on the top and bottom of the block. Axial stress is calculated by summing the vertical (z) reaction forces of all the top and bottom gridpoints and dividing by twice the cross-sectional area. The axial strain is simply the sum of displacement of the top and bottom gridpoints divided by the original length.

The model is then cycled for 35,000 steps. The model solve command is not used because the model will never reach equilibrium.

Results and Discussion

The axial stress versus axial strain curve from the 3DEC simulation is shown in Figure 2. A peak stress of ~752 MPa is observed, which is close to the value obtained in Lan et al (2013).

A cross-section of the “cracks” that form are shown in Figure 3. This figure is generated by plotting the joints, contouring by normal displacement and then checking the box to specify an aperture threshold of 1e-5 m, so that only the open joints are plotted.

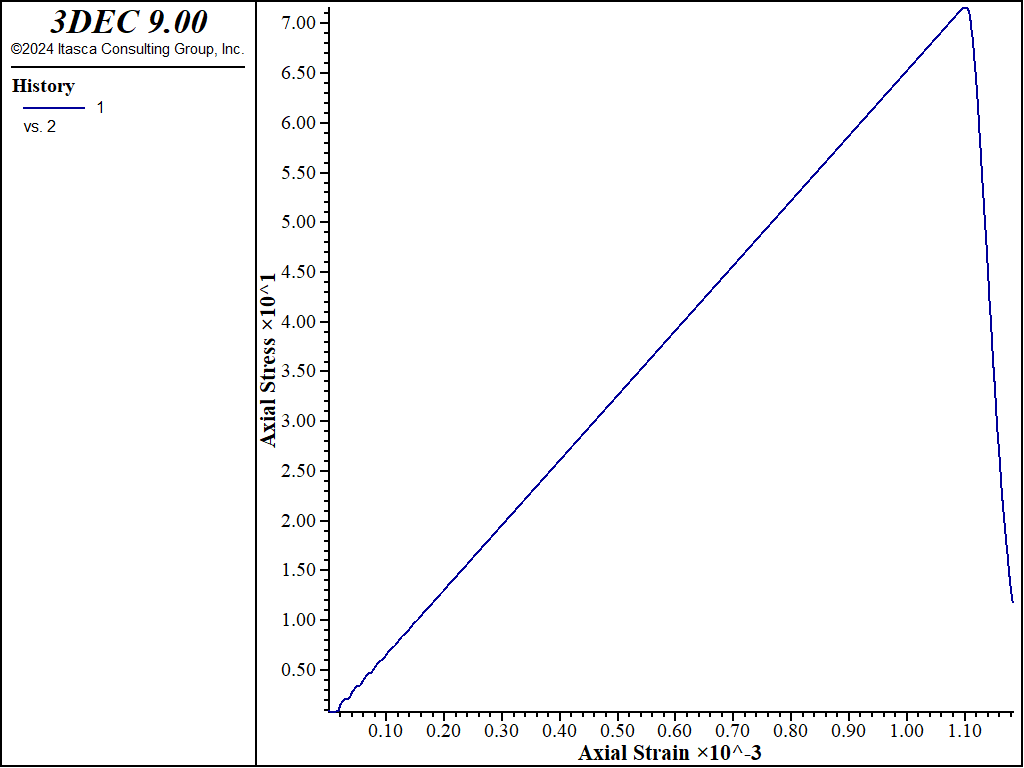
../../../../_images/ucs-voro-ss.png

Figure 2: Axial stress versus axial strain in the UCS test.

../../../../_images/ucs-voro-cracks.png

Figure 3: Cracks at the end of the UCS test. The normal displacement on the joints are plotted if the normal displacement (opening) exceeds 0.01 mm.

References

Lan, H., Martin, C.D., Qi, S. and Li, T., 2013. A 3D grain based model for characterizing the geometric heterogeneity of brittle rock, in Proceedings of the 47th U.S. Rock Mechanics / Geomechanics Symposium, San Francisco, CA, USA, 23-26 June, American Rock Mechanics Association.

Data Files

sample.dat

model new
model random 10000
block tolerance 1e-6

; make parallelepiped to fill with voronois
geometry import 'parallelepiped.dxf'
block generate voronoi maximum-edge 0.006

; cut out cylinder to prevent alignment of voronois along the edges
model domain extent -1 1
geometry import 'cylinder.dxf'
block cut geometry 'cylinder'

block delete range cylinder end-1 0 0 0 end-2 0 0 0.125 radius 0.025 not
model save 'voro_rigid.sav'

;model restore 'voro_rigid.sav'
block zone generate-new maximum-edge 0.002

; delete blocks that didn't zone
block delete range deformable not

model save 'voro_defor.sav'

ucs_test.dat

model restore 'voro_defor'
model large-strain on 

; properties in MPa
block zone cmodel assign elastic 
block zone property young 76e3 pois 0.25 density 0.002
block contact jmodel mohr
block contact property  stiffness-normal 7.6e7 stiffness-shear 7.6e7 ...
  cohesion 40 tension 14.4 friction 10
block contact material-table default property stiffness-normal 7.6e7 ...
  stiffness-shear 7.6e7 friction 10

block gridpoint group 'top' range position-z 0.125
block gridpoint group 'bottom' range position-z 0.

block gridpoint apply velocity-z -0.05 range group 'top'
block gridpoint apply velocity-z 0.05 range group 'bottom'

model cycle 1

; make lists of gridpoints forigin monitoring reaction forces
[global area = math.pi*0.025^2]
[global length = 0.125]

fish define findList
    gp_list_top = list
    gp_list_bottom = list
    loop foreach gp block.gp.list
        if block.gp.isgroup(gp,'top')
            gp_list_top("end") = gp
        endif
        if block.gp.isgroup(gp,'bottom')
            gp_list_bottom("end") = gp
        endif
    endloop
end
[findList]
[global gp_top = gp_list_top(1)]

fish define zzstress
  ; compression positive,unit MPa
  local top_reaction    = -list.sum(block.gp.force.reaction.z(::gp_list_top))
  local bottom_reaction = list.sum(block.gp.force.reaction.z(::gp_list_bottom))
 
  zzstress = 0.5*(top_reaction + bottom_reaction)/area
  zzstrain = -2.0*block.gp.disp.z(gp_top)/length
end

fish history zzstress
fish history zzstrain

model cycle 30000
model save 'ucs.sav'

Endnote