Natural Modes of Oscillation
For many problems, the important frequencies are related to the natural mode of oscillation of the system. Examples of this type of problem include seismic analysis of surface structures such as dams or dynamic analysis of underground excavations.
For these problems, the fundamental frequency, \(f\), associated with the natural mode of oscillation is
where:
\(C\) = speed of propagation associated with the mode of oscillation; and
\(\gamma\) = longest wavelength.
For an elastic continuous system, the speed of propagation, \(C_p\), is given by \(C_p = [(K + 4/3\ G) / \rho]^{1/2}\) for \(p\)-waves, and \(C_s = (G/\rho)^{1/2}\) for \(s\)-waves, where \(K\) = bulk modulus, \(G\) = shear modulus, and \(\rho\) = density.
The longest wavelength, characteristic length or fundamental wavelength depends on boundary conditions. Consider a solid bar of length 1 with boundary conditions, as shown in the figure below (part (a)). The fundamental mode shapes for cases (1), (2), and (3) are as shown in part (b).
If shear motion of the bar gives rise to the lowest natural mode, then \(C_s\) is used in the preceding equation; otherwise, \(C_p\) is used if motion parallel to the axis of the bar gives rise to the lowest natural mode.
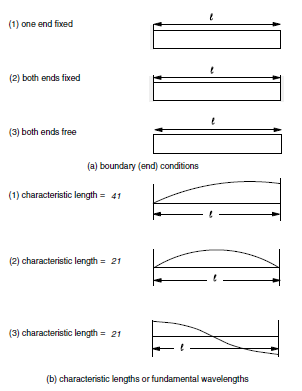
Figure 1: Comparison of fundamental wavelengths for bars with varying end conditions.
Example Problems (from Cundall et al. (1979), pp. 71-73)
In the limit of very high joint stiffness, an assemblage of blocks should resemble a continuum, both statically and dynamically. Consider the problem of eight square deformable blocks resting on a rigid base. Three problems can be treated: an unconfined column; a confined column in compression; and a column in shear.
The column is loaded by applying gravity in either the \(x\)- or \(z\)-direction. For the dynamic case, the mass damping is zero, with stiffness-proportional damping as follows:
fraction of critical = 0.1
frequency = 10.0
The case of confined compression is modeled by inhibiting lateral displacement along the vertical boundaries, which prevents lateral deformation of the blocks. For unconfined compression, lateral displacement is not inhibited. For the column in shear, vertical motion along all boundaries is inhibited. Other properties are:
bulk modulus |
\(K\) = 1.5 × 104 |
for compression tests |
shear modulus |
\(G\) = 0.428562 × 104 |
for compression tests |
Poisson’s ratio |
0.4 |
for compression tests |
bulk modulus |
\(K\) = 1.0 × 104 |
for shear tests |
shear modulus |
\(G\) = 1.0 × 104 |
for shear tests |
density |
\(\rho\) = 1.0 |
|
applied gravity |
\(g_y\) = -1.0 |
for compression tests |
\(g_y\) = 0.1 |
for shear tests |
|
column height |
\(L\) = 800 |
|
column width |
\(W\) = 100 |
|
number of blocks |
\(n\) = 8 |
The moduli appropriate to the various modes of deformation are given below.
Confined Compression |
Unconfined Compression |
Shear |
|---|---|---|
\(K + (4/3)\ G\) |
\(4 G\ \biggl[ {{(1/3)\ G + K} \over {K + (4/3)\ G}} \biggr]\) |
\(G\) |
(plane strain, Young’s modulus) |
||
2.5714 × 104 |
1.4286 × 104 |
1.0 × 104 |
Table 3 compares the theoretical periods and calculated (3DEC) natural periods of oscillation. The theoretical values for natural period of oscillation are calculated as
natural period, \(T = 4 L\ \sqrt{(\rho / E^*)}\)
where \(E^*\) is the appropriate modulus selected from Table 2.
Confined Compression |
Unconfined Compression |
Shear |
|
|---|---|---|---|
Theoretical |
19.96 |
26.77 |
32.00 |
3DEC |
20.47 |
27.83 |
32.24 |
The data file for each of these problems is listed.
Data File - Confined Compression
;-----------------------------------------------------------------------
; Natural periods of an Elastic Column: Confined compression
;-----------------------------------------------------------------------
model new
model title "Natural periods of an Elastic Column: Confined"
model configure dynamic
model large-strain on
;geometry
block create brick -50,50 -50,50 -400,400
block cut joint-set dip 0 dip-direction 180 origin 0,0,0 ...
spacing 100 number = 7
; zones
block zone generate edgelength 200
block zone cmodel assign elastic
block zone property bulk 2e4 shear 0.428562e4 density 1
; joints
block contact jmodel assign elastic
block contact property stiffness-normal 4e5 stiffness-shear 4e5
block contact material-table default property stiffness-normal 4e5 ...
stiffness-shear 4e5
; boundary conditions
block gridpoint apply velocity-x 0 range position-x -50
block gridpoint apply velocity-x 0 range position-x 50
block gridpoint apply velocity-y 0 range position-y -50
block gridpoint apply velocity-y 0 range position-y 50
block gridpoint apply velocity-z 0 range position-z -400
; program call fish functions used to determine period
program call "period.fis"
model gravity 0 0 -1.0
history interval 100
fish history z_dis
model history dynamic time-total
block mechanical damping rayleigh 0.1 1.0 stiffness
model solve time-total 11
[print_period]
Data File - Unconfined Compression
;-----------------------------------------------------------------------
; Natural periods of an Elastic Column: Confined compression
;-----------------------------------------------------------------------
model new
model title "Natural periods of an Elastic Column: Unconfined"
model configure dynamic
model large-strain on
;geometry
block create brick -50,50 -50,50 -400,400
block cut joint-set dip 0 dip-direction 180 origin 0,0,0 ...
spacing 100 number = 7
; zones
block zone generate edgelength 200
block zone cmodel assign elastic
block zone property bulk 2e4 shear 0.428562e4 density 1
; joints
block contact jmodel assign elastic
block contact property stiffness-normal 4e5 stiffness-shear 4e5
block contact material-table default property stiffness-normal 4e5 ...
stiffness-shear 4e5
; boundary conditions
block gridpoint apply velocity-z 0 range position-z -400
; program call fish functions used to determine period
program call "period.fis"
model gravity 0 0 -1.0
history interval 100
fish history z_dis
model history dynamic time-total
block mechanical damping rayleigh 0.1 1.0 stiffness
model solve time-total 15
[print_period]
Data File - Shear
;-----------------------------------------------------------------------
; Natural periods of an Elastic Column: Shear
;-----------------------------------------------------------------------
model new
model title "Natural periods of an Elastic Column: Shear"
model configure dynamic
model large-strain on
;geometry
block create brick -50,50 -50,50 -400,400
block cut joint-set dip 0 dip-direction 180 origin 0,0,0 ...
spacing 100 number = 7
; zones
block zone generate edgelength 200
block zone cmodel assign elastic
block zone property bulk 2e4 shear 1e4 density 1
; joints
block contact jmodel assign elastic
block contact property stiffness-normal 4e5 stiffness-shear 4e5
block contact material-table default property stiffness-normal 4e5 ...
stiffness-shear 4e5
; boundary conditions
block gridpoint apply velocity-z 0 range position-x -50
block gridpoint apply velocity-z 0 range position-x 50
block gridpoint apply velocity-z 0 range position-y -50
block gridpoint apply velocity-z 0 range position-y 50
block gridpoint apply velocity-x 0 range position-z -400
; program call fish functions used to determine period
program call "period.fis"
model gravity 0.1,0,0
history interval 100
fish history x_dis
model history dynamic time-total
block mechanical damping rayleigh 0.1 1.0 stiffness
model solve time-total 17
[print_period]
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Nov 12, 2025 |
