Linear Contact Bond Model
The linear contact bond model with inactive dashpots and a reference gap of zero corresponds with the contact-bond model of Potyondy and Cundall (2004). It is a linear-based model that is referred to in commands and FISH by the name linearcbond.
Introduction
A contact bond can be envisioned as a pair of elastic springs (or a point of glue) with constant normal and shear stiffnesses acting at the contact point. These two springs have specified tensile and shear strengths. The existence of a contact bond precludes the possibility of slip whereby the shear force is limited by the product of the friction coefficient and normal force; instead, the shear force is limited by the shear strength. Contact bonds allow tensile forces to develop at a contact with a gap. The tensile force is limited by the tensile strength.
If the normal force exceeds the tensile strength, the bond breaks, and both the normal and shear forces are set to zero. If the shear force exceeds the shear strength, the bond breaks, but the contact forces are not altered, provided that the shear force does not exceed the product of the friction coefficient and normal force, and provided that the normal force is compressive.
Behavior Summary
The linear contact bond model provides the behavior of an infinitesimal, linear elastic and either bonded or frictional interface that carries a force (see Figure 1). The interface does not resist relative rotation and is either bonded or unbonded. If bonded, the behavior is linear elastic until the strength limit is exceeded and the bond breaks, making the interface unbonded. If unbonded, the behavior is linear elastic and frictional with slip being accommodated by imposing a Coulomb limit on the shear force. The unbonded linear contact bond model is equivalent to the linear model.
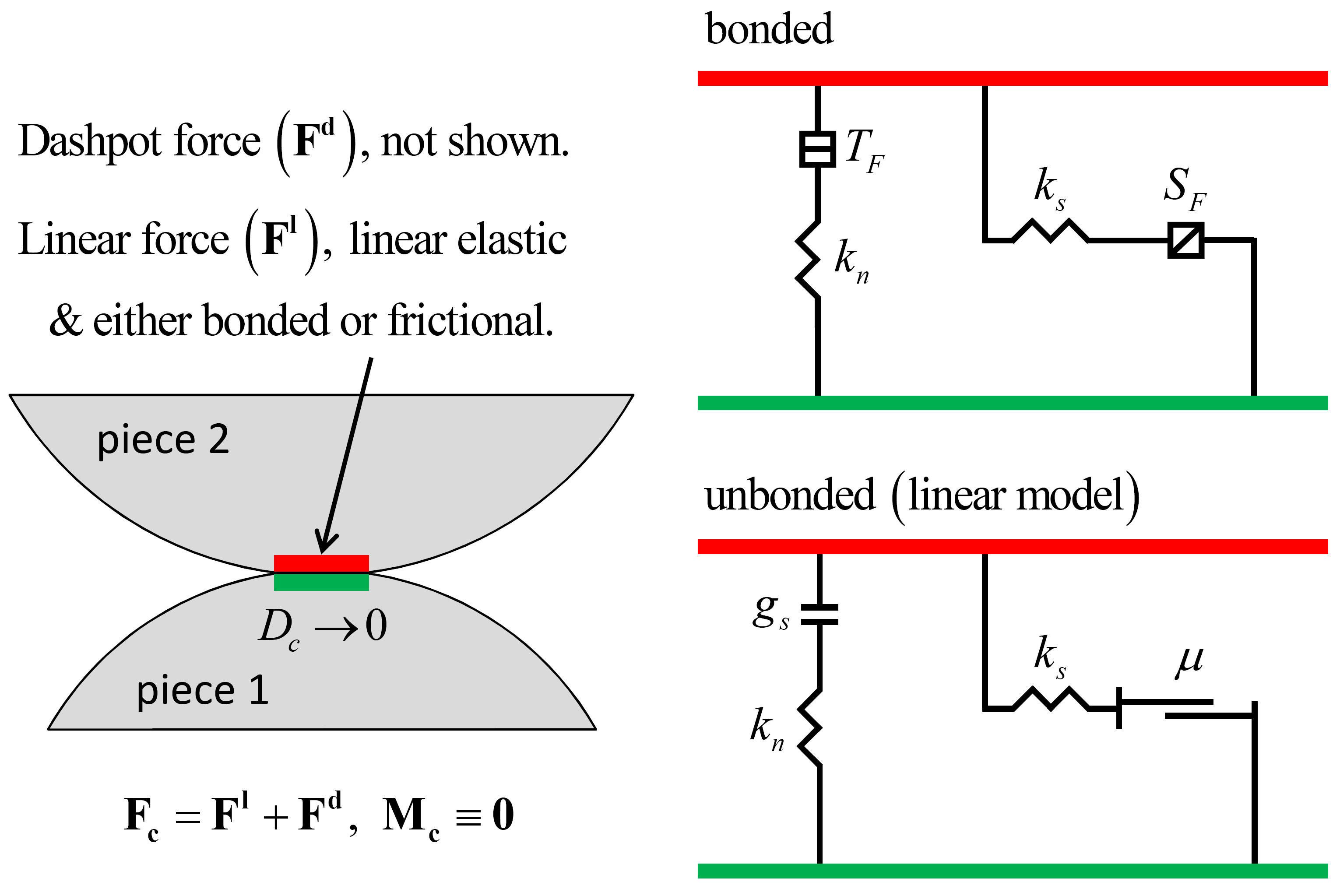
Figure 1: Behavior and rheological components of the linear contact bond model with inactive dashpots.
Activity-Deletion Criteria
A contact with the linear contact bond model is active if it is bonded or if the surface gap is less than or equal to zero. The force-displacement law is skipped for inactive contacts. The surface gap is shown in this figure of the linear formulation. When the reference gap is zero, the notional surfaces coincide with the piece surfaces.
Force-Displacement Law
The behavior for an unbonded linear contact bond model is equivalent to that of the linear model (see this section). The present discussion describes the bonded case. The force-displacement law for a bonded linear contact bond model differs from that of the linear model: (a) the linear force can become tensile; (b) slip cannot occur (slip can occur after the bond breaks); (c) the dashpot no-tension modes \((M_{d} =\left\{1,3\right\})\) are deactivated such that the dashpot force can become tensile; and (d) the dashpot slip-cut modes \((M_{d} =\left\{2,3\right\})\) are deactivated such that the dashpot force does not depend on the slip state.
The update of the linear normal force depends on the normal-force update mode \(M_l\). When \(M_l=0\) (i.e., absolute normal-force update mode is active), the normal force becomes
When \(M_l=1\) (i.e., incremental normal-force update mode is active), the normal force becomes
Equations (1) and (2) differ from this equation of the linear section in which the no-tension behavior is enforced. No-tension behavior is not enforced when a contact bond is present.
The update of the linear shear force becomes
Equation (3) differs from this equation of the linear section in which the Coulomb-slip condition is enforced. Slip cannot occur when a contact bond is present.
The update of the dashpot normal force becomes
Equation (4) differs from this equation of the linear section in which no-tension behavior is enforced. The dashpot force can become tensile when a contact bond is present.
The update of the dashpot shear force becomes
Equation (5) differs from this equation of the linear section in which slip-cut behavior is enforced. The dashpot force does not depend on the slip state when a contact bond is present.
Enforce the strength limits (see Figure 2). If the tensile-strength limit is exceeded \(\left(F_{n}^{l} >T_{F} \right)\), then break the bond in tension:
If the bond has not broken in tension, then enforce the shear strength limit. If the shear-strength limit is exceeded \(\left(\left\| \mathbf{F_{s}^{l}} \right\| >S_{F} \right)\), then break the bond in shear:
If the bond has broken, then trigger the bond_break callback event. The strength limits are enforced prior to the enforcement of the slip condition and update of the dashpot force.
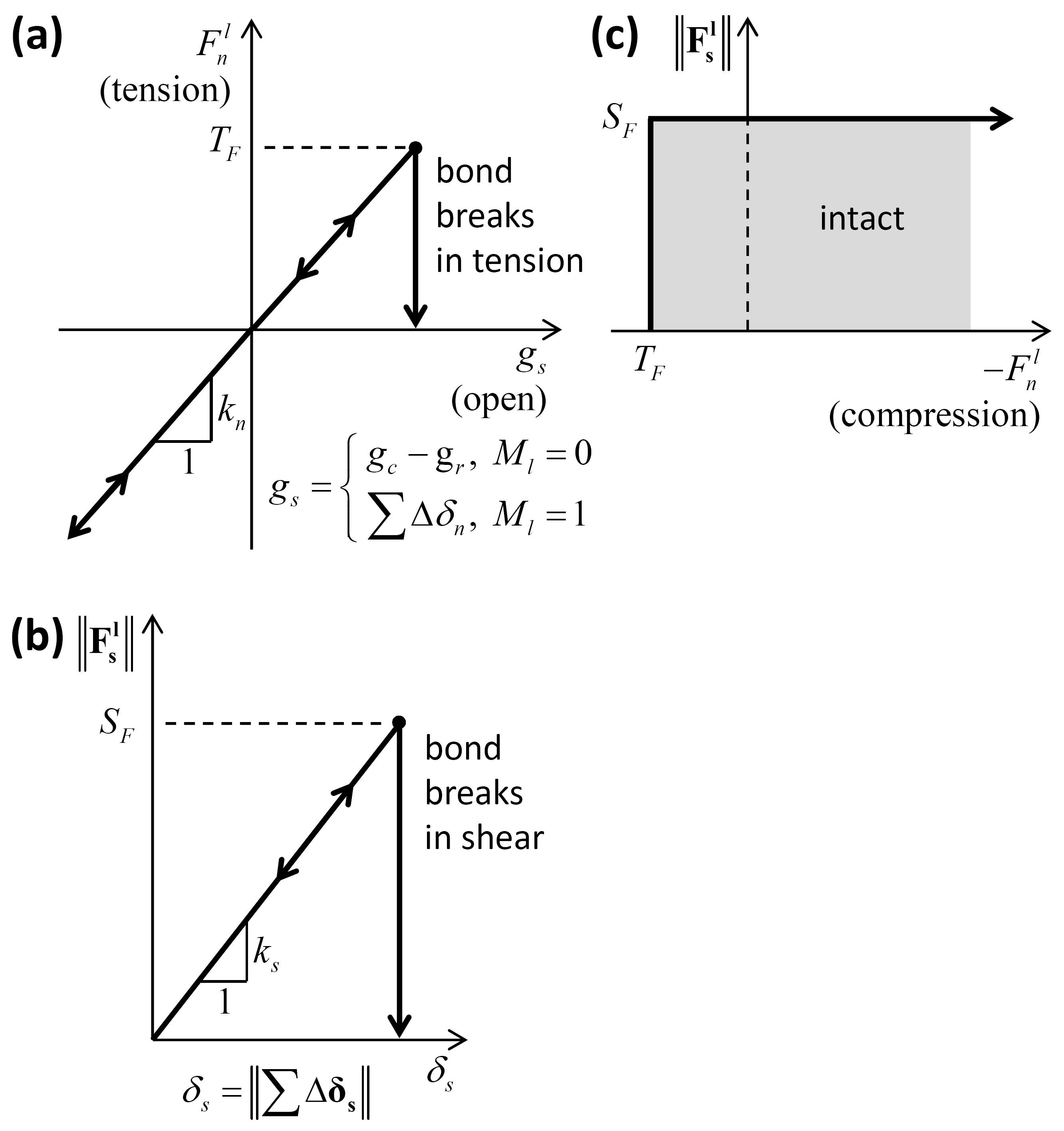
Figure 2: Force-displacement law for the linear component of the bonded linear contact bond model: (a) normal force versus surface gap, (b) shear force versus relative shear displacement and (c) failure envelope.
Energy Partitions
The linear contact bond model provides three energy partitions:
strain energy, \(E_{k}\), stored in the linear springs;
slip energy, \(E_{\mu }\), defined as the total energy dissipated by frictional slip; and
dashpot energy, \(E_{\beta }\), defined as the total energy dissipated by the dashpots.
The strain energy, slip energy, and dashpot energy are updated as for the linear model (see this section). The slip energy remains equal to zero until the bond breaks. The table below lists these energy partitions (together with the keywords by which they are referred to in commands and FISH).
Keyword |
Symbol |
Description |
Range |
Accumulated |
|---|---|---|---|---|
Linear Group: |
||||
|
\(E_{k}\) |
strain energy |
\([0.0,+\infty)\) |
NO |
|
\(E_{\mu}\) |
total energy dissipated by slip |
\((-\infty,0.0]\) |
YES |
Dashpot Group: |
||||
|
\(E_{\beta}\) |
total energy dissipated by dashpots |
\((-\infty,0.0]\) |
YES |
Properties
The properties defined by the linear contact bond model are listed in the table below for a concise reference; see the “Contact Properties” section for a description of the information in the table columns. The mapping from the surface inheritable properties to the contact model properties is also discussed below.
Keyword |
Symbol |
Description |
Type |
Range |
Default |
Modifiable |
Inheritable |
|---|---|---|---|---|---|---|---|
linearcbond |
Model name |
||||||
Linear Group: |
|||||||
kn |
\(k_n\) |
Normal stiffness [force/length] |
FLT |
\([0.0,+\infty)\) |
0.0 |
YES |
YES |
ks |
\(k_s\) |
Shear stiffness [force/length] |
FLT |
\([0.0,+\infty)\) |
0.0 |
YES |
YES |
fric |
\(\mu\) |
Friction coefficient [-] |
FLT |
\([0.0,+\infty)\) |
0.0 |
YES |
YES |
rgap |
\(g_r\) |
Reference gap [length] |
FLT |
\(\mathbb{R}\) |
0.0 |
YES |
NO |
lin_mode |
\(M_l\) |
Normal-force update mode [-] |
INT |
\(\{0,1\}\) |
0 |
YES |
NO |
\(\;\;\;\;\;\;\begin{cases} \mbox{0: update is absolute} \\ \mbox{1: update is incremental} \end{cases}\) |
|||||||
emod |
\(E^*\) |
Effective modulus [force/area] |
FLT |
\([0.0,+\infty)\) |
0.0 |
NO\(^1\) |
N/A |
kratio |
\(\kappa^*\) |
Normal-to-shear stiffness ratio [-] |
FLT |
\([0.0,+\infty)\) |
0.0\(^2\) |
NO\(^1\) |
N/A |
\(\kappa^* \equiv \frac{k_n}{k_s}\) |
|||||||
lin_slip |
\(s\) |
Slip state [-] |
BOOL |
{false,true} |
false |
NO |
N/A |
\(\;\;\;\;\;\;\begin{cases} \mbox{true: slipping} \\ \mbox{false: not slipping} \end{cases}\) |
|||||||
lin_force |
\(\mathbf{F^l}\) |
Linear force (contact plane coord. system) |
VEC |
\(\mathbb{R}^3\) |
\(\mathbf{0}\) |
YES |
NO |
\(\left( -F_n^l,F_{ss}^l,F_{st}^l \right) \quad \left(\mbox{2D model: } F_{ss}^l \equiv 0 \right)\) |
|||||||
user_area |
\(A\) |
Constant area [length*length] |
FLT |
\((0.0,+\infty)\) |
0.0 |
YES |
NO |
Dashpot Group: |
|||||||
dp_nratio |
\(\beta_n\) |
Normal critical damping ratio [-] |
FLT |
\([0.0,1.0]\) |
0.0 |
YES |
NO |
dp_sratio |
\(\beta_s\) |
Shear critical damping ratio [-] |
FLT |
\([0.0,1.0]\) |
0.0 |
YES |
NO |
dp_mode |
\(M_d\) |
Dashpot mode [-] |
INT |
{0,1,2,3} |
0 |
YES |
NO |
\(\;\;\;\;\;\;\begin{cases} \mbox{0: full normal & full shear} \\ \mbox{1: no-tension normal & full shear} \\ \mbox{2: full normal & slip-cut shear} \\ \mbox{3: no-tension normal & slip-cut shear} \end{cases}\) |
|||||||
dp_force |
\(\mathbf{F^d}\) |
Dashpot force (contact plane coord. system) |
VEC |
\(\mathbb{R}^3\) |
\(\mathbf{0}\) |
NO |
NO |
\(\left( -F_n^d,F_{ss}^d,F_{st}^d \right) \quad \left(\mbox{2D model: } F_{ss}^d \equiv 0 \right)\) |
|||||||
Contact-Bond Group: |
|||||||
cb_tenf |
\(T_F\) |
Tensile strength [force] |
FLT |
\([0.0,+\infty)\) |
0.0 |
YES |
NO |
cb_shearf |
\(S_F\) |
Shear strength [force] |
FLT |
\([0.0,+\infty)\) |
0.0 |
YES |
NO |
cb_tens |
\(T_{\sigma }\) |
Tensile strength [stress] |
FLT |
\([0.0,+\infty)\) |
0.0 |
NO |
NO |
cb_shears |
\(S_{\sigma }\) |
Shear strength [stress] |
FLT |
\([0.0,+\infty)\) |
0.0 |
NO |
NO |
cb_state |
\(B\) |
Bond state |
INT |
{0,1,2,3} |
0 |
NO |
NO |
\(\;\;\;\;\;\;\begin{cases} \mbox{0: unbonded} \\ \mbox{1: unbonded & broke in tension} \\ \mbox{2: unbonded & broke in shear} \\ \mbox{3: bonded} \end{cases}\) |
|||||||
\(^1\) This property is set by the deformability method. |
|||||||
\(^2\) By convention, \(\kappa^* = 0.0\) if either the normal or shear stiffness is 0. |
|||||||
Note
Out-of-balance forces acting on bodies are accumulated during force-displacement calculations. Modifying the forces stored in the contact models will not alter them instantaneously. Therefore, any change to \(\mathbf{F^l}\) may only be effective during the next force-displacement calculation. When \(M_l = 0\), the normal component of the linear force is automatically overridden during the next force-displacement calculation.
Surface Property Inheritance
The linear stiffnesses, \(k_n\) and \(k_s\), and the friction coefficient, \(\mu\), may be inherited from the contacting pieces. See this section from the linear formulation for details on property inheritance.
Methods
Method |
Arguments |
Symbol |
Type |
Range |
Default |
Description |
|---|---|---|---|---|---|---|
Linear Group: |
||||||
area |
Set user_area to the area |
|||||
deformability |
Set deformability |
|||||
emod |
\(E^*\) |
FLT |
\([0.0,+\infty)\) |
N/A |
Effective modulus |
|
kratio |
\(\kappa^*\) |
FLT |
\([0.0,+\infty)^*\) |
N/A |
Normal-to-shear stiffness ratio |
|
Contact-Bond Group: |
||||||
bond |
Bond the contact if \(g_c \in G\) |
|||||
gap |
\(G\) |
VEC2 |
\(\mathbb{R}^2\) |
\((-\infty,0]\) |
Gap interval |
|
unbond |
Unbond the contact if \(g_c \in G\) |
|||||
gap |
\(G\) |
VEC2 |
\(\mathbb{R}^2\) |
\((-\infty,0]\) |
Gap interval |
|
cb_strength |
Set tensile and shear strength |
|||||
tensile |
\(T_\sigma\) |
FLT |
\([0.0,+\infty)\) |
N/A |
Tensile strength [stress] |
|
shear |
\(S_\sigma\) |
FLT |
\([0.0,+\infty)\) |
N/A |
Shear strength [stress] |
|
\(^*\) By convention, setting \(\kappa^* = 0.0\) sets \(k_s = 0.0\) but does not alter \(k_n\). |
||||||
Area
Set the user_area property via the current contact area. This operation means that the contact area stays constant and is fixed independent of changes to the piece sizes/geometries. In order for the stiffnesses to be recomputed accounting for this area, one should subsequently call the deformabilty method.
Deformability
See this section from the linear formulation for details on this method.
Bond
Create a contact bond by bonding the interface if the contact gap between the pieces is within the bonding-gap interval. If no gap is specified, then the interface is bonded if the pieces overlap. A single value can be specified with the gap keyword corresponding to the maximum gap. One can ensure the existence of contacts between all pieces with a contact gap less than a specified bonding gap \((g_b)\) by specifying \(g_b\) as the proximity in the contact cmat default command of the Contact Model Assignment Table (CMAT).
Unbond
Remove a contact bond by unbonding the interface if the contact gap between the pieces is within the bonding-gap interval. If no gap is specified, then the interface is unbonded if the pieces overlap. A single value can be specified with the gap keyword corresponding to the maximum gap. If the interface becomes unbonded, then the bond state becomes unbonded (\(B=0\)). The linear force is unaffected and will be updated during the next cycle.
cb_strength
The strengths in stress units (\(T_{\sigma }\) and \(S_{\sigma }\)) are the arguments of the cb_strength method, which sets the strengths in force units (\(T_{F}\) and \(S_{F}\)):
using the area of the volume of material shown in this figure of the linear formulation. Note that the user_area property can be used to override this volume, specifying the area of the contact directly.
Callback Events
Event |
Array Slot |
Value Type |
Range |
Description |
|---|---|---|---|---|
contact_activated |
Contact has become active |
|||
1 |
C_PNT |
N/A |
Contact pointer |
|
Linear Group: |
||||
slip_change |
Slip state has changed |
|||
1 |
C_PNT |
N/A |
Contact pointer |
|
2 |
INT |
{0,1} |
Slip change mode |
|
\(\;\;\;\;\;\;\begin{cases} \mbox{0: slip has initiated} \\ \mbox{1: slip has ended} \end{cases}\) |
||||
Contact-Bond Group: |
||||
bond_break |
Bond has broken |
|||
1 |
C_PNT |
N/A |
Contact pointer |
|
2 |
INT |
{1,2} |
Failure mode |
|
\(\;\;\;\;\;\;\begin{cases} \mbox{1: failed in tension} \\ \mbox{2: failed in shear} \end{cases}\) |
||||
3 |
FLT |
\([0.0,+\infty)\) |
Failure strength [force] (\(T_F\) or \(S_F\), according to the failure mode) |
|
Usage and Verification Examples
Bonded-particle models can be constructed with the linear contact bond model. A contact-bonded material (defined here) can be created with the Material Modeling Support Package.
to do items listed below
Example 1: Simple Model
Use the cmat and the distribute command to assemble an assembly of balls. Install bonds using the contact property command.
Alternatively install bonds and modify properties using the contact model methods.
Example 2: Verification Example
Exercize the force-displacement law for a ball-ball contact - normal and shear loading. Perform a rigid body rotation of the system and follow the forces in the local and global system.
Example 3: Fishcall events
Exercise the different fischall events.
Model Summary
An alphabetical list of the linear contact bond model methods is given here. An alphabetical list of the linear contact bond model properties is given here.
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Nov 12, 2025 |
