Hollow Sphere Subject to an Internal Blast

Note

To view this project in FLAC3D, use the menu command Help ‣ Examples…. The main data files used are shown at the end of this example. The remaining data files can be found in the project.

This problem concerns the propagation of a spherical wave due to an impulsive pressure (explosion) in a sphere. In unbounded (i.e., infinite) media, two types of waves can exist: compression and shear waves. In this problem, the axisymmetric nature of the problem eliminates the shear wave. Therefore, only the solution for the compression wave need be sought. The problem provides a test of the dynamic capabilities of FLAC3D and is applicable to impact and explosion modeling.

The analytical solution for this problem, assuming that the material is elastic and isotropic, was derived by Blake (1952). The solution is based on the following governing equation:

\[{{\partial^2 \phi} \over {\partial t^2}} = C_p^2\ \bigtriangledown^2 \phi\]

where:

\(C_p\)

= compressional wave velocity;

\(t\)

= time;

\(\phi\)

= a potential function; and

\(\bigtriangledown^2\)

= Laplacian operator.

Let \(p(t)\) be an impulse that jumps from zero to \(p_0\) at \(t\) = 0, and then decays exponentially with the time constant \(\alpha^{-1}\). Thus, the pressure function can be defined by

\[\begin{split}\begin{split} p(t) &= p_0\ e^{- \alpha t} \qquad \rm{for} \; \; t \ge 0 \\ p(t) &= 0 \qquad \qquad \; \rm{for} \; \; t < 0 \end{split}\end{split}\]

A step function of the pressure (\(\alpha\) = 0) will be used for this problem. For such a pressure function, the potential function that satisfies the governing equation is

\[\phi_{\alpha = 0} = {{p_0\ a^3 K} \over {\rho\ C_p^2\ r}}\ \biggl[\ - 1 + \sqrt{{{4 K} \over {4 K -1}}}\ \exp (- \alpha_0 \tau)\ \cos \biggl(\ \omega_0\ \tau - \tan^{-1}\ {{1} \over {\sqrt{4 K -1}}}\ \biggr)\ \biggr]\]

where:

\(a\)

= radius of the sphere;

\(K\)

= \({{1 - \nu} \over {2 (1 - 2 \nu)}}\);

\(\nu\)

= Poisson’s ratio;

\(r\)

= radial coordinate;

\(\alpha_0\)

= \({{C_p} \over {2 a K}}\) = radiation damping constant;

\(\tau\)

= \(t - {{ r - a} \over {C_p}}\); and

\(\omega_0\)

= \({{c} \over {2 a K}}\ \sqrt{4 K - 1}\) = natural frequency.

The radial displacement can be found by differentiating the potential function with respect to radial distance.

\[u_r = {{\partial \phi} \over {\partial r}} = - {{p_0 a^3 K} \over {\rho\ C_p^2\ r^2}}\ \biggl[\ - 1 + \sqrt{2 - 2 \nu}\ \exp (- \alpha_0 \ \tau)\ \cos \left({\omega_0 \tau - \tan^{-1} \ {1 \over \sqrt{4 K - 1}} }\right)\ \biggr]\]
\[+ {{p_0\ a^3 K} \over {\rho\ C_p^2\ r}}\ \biggr[\ {{\alpha_0} \over {C_p}}\ \sqrt{2 - 2 \nu}\ \exp (- \alpha_0 \tau)\ \cos \left({\omega_0\ \tau - \tan^{- 1} \ {1 \over \sqrt{4 K - 1}}}\right)\]
\[+ {{\omega_0} \over {C_p}}\ \sqrt{2 - 2 \nu}\ \exp (- \alpha_0\ \tau)\ \sin \left({\omega_0\ \tau - \tan^{- 1}\ {1 \over \sqrt{4 K - 1}}}\right) \ \biggr]\]

A sphere embedded in an infinite, isotropic medium is simulated in two ways. Figures 1 and 2 show two different grids used for the simulation. The first grid is a one-dimensional representation in which a narrow, tapering tube with roller boundaries on all sides approximates the condition of spherical symmetry. The second grid is fully three-dimensional, but it is bounded by three symmetry planes (i.e., one-eighth of the problem is modeled). The radius of the inner boundary is assumed to be 10 m, and the outer boundary is located at a distance ten times that of the inner boundary for the 1D case.

For both grids, normal movement is prevented at the axes of symmetry, and a viscous condition is imposed on the outer boundary to absorb the wave. The material properties used for the problem are

shear modulus (\(G\))

1 × 1010

bulk modulus (\(K\))

1.665 × 1010 Pa

density (\(\rho\))

1675 kg/m3

A pressure equal to 1000 Pa is applied at the inner boundary to simulate the blasting.

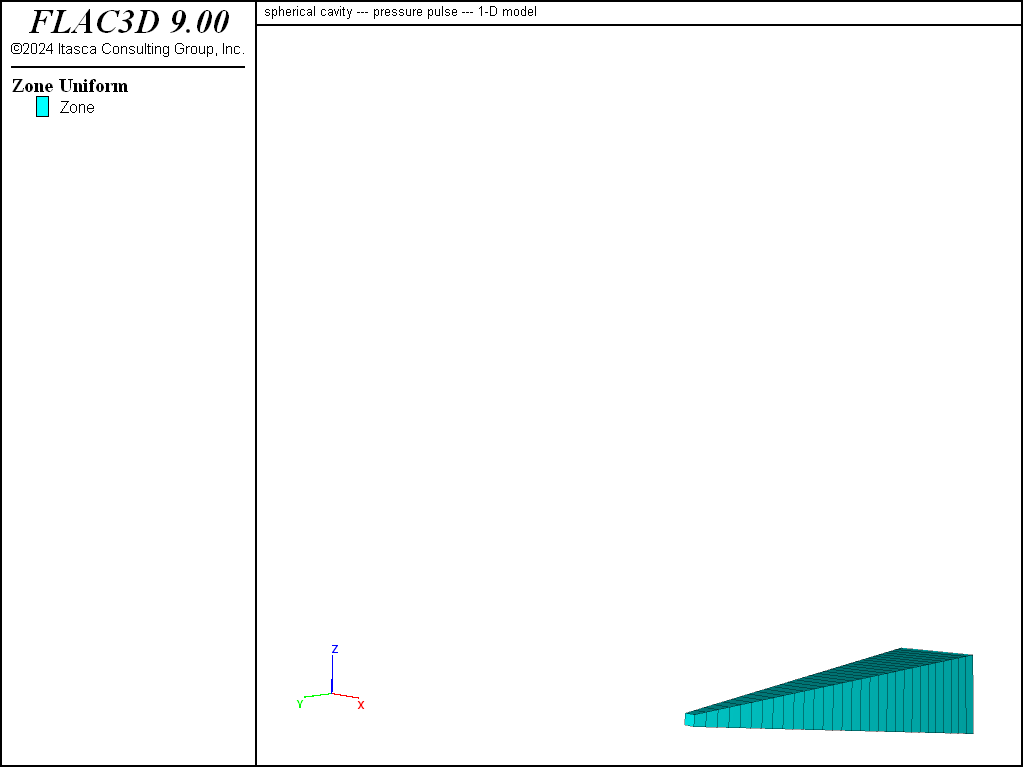
click to enlarge in a new window

Figure 1: 1D grid to approximate spherical symmetry.

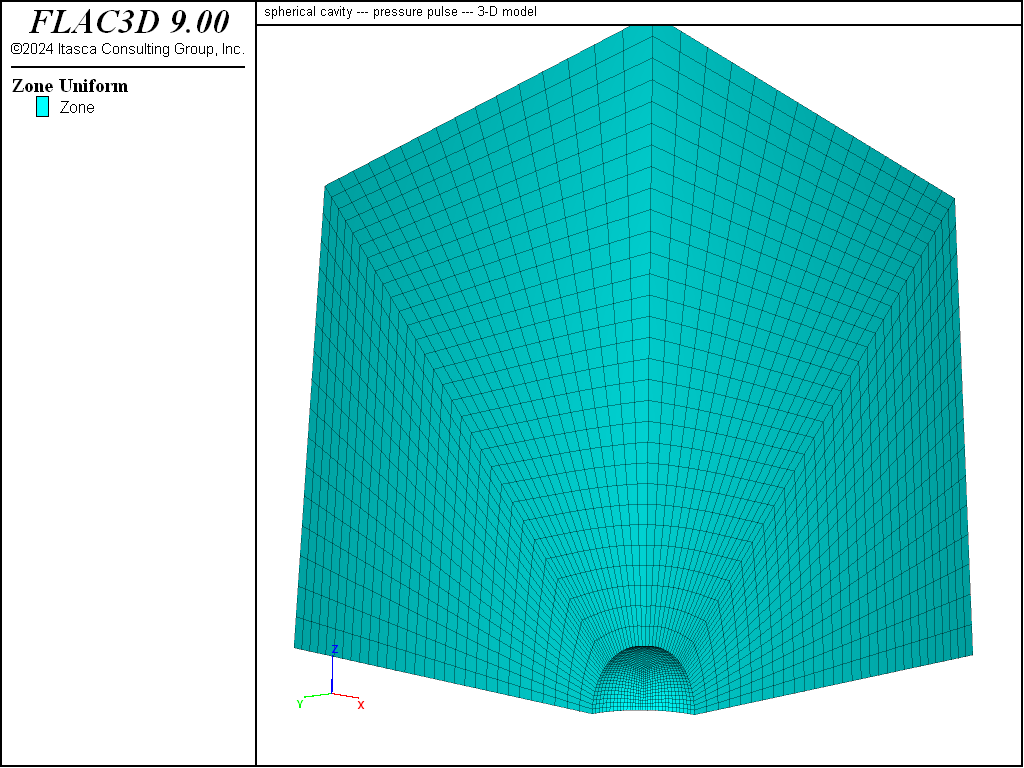
click to enlarge in a new window

Figure 2: 3D grid—one-eighth of problem is modeled.

The radial displacement histories recorded up to 0.1 second at \(r\) = 2.05\(a\), 3.42\(a\), and 4.87\(a\) are given in Figures 3 and 4 for the one-dimensional and three-dimensional simulation, respectively. The delay of the response at locations far from the sphere can be noted in both cases. In both cases, FLAC3D is able to capture the response at peak and steady states. The fluctuation at late time is due to the fact that the radiated wave is not absorbed completely by the viscous boundary.

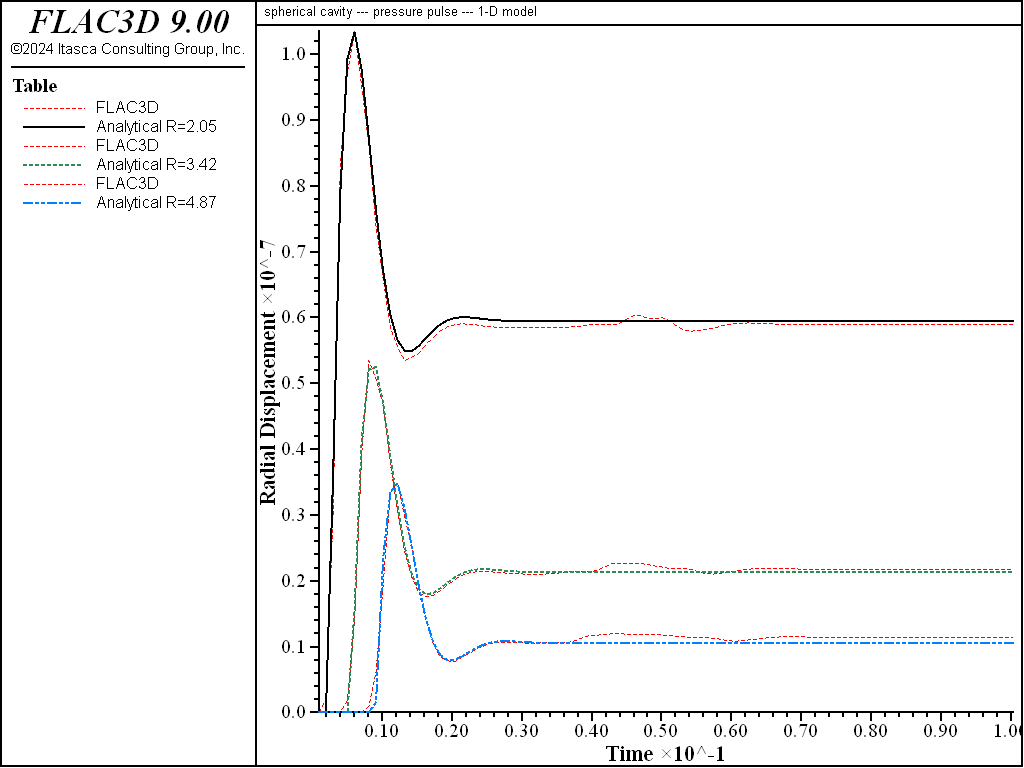
click to enlarge in a new window

Figure 3: Radial displacement histories at r = 2.05a, 3.42a, and 4.87a (1D case).

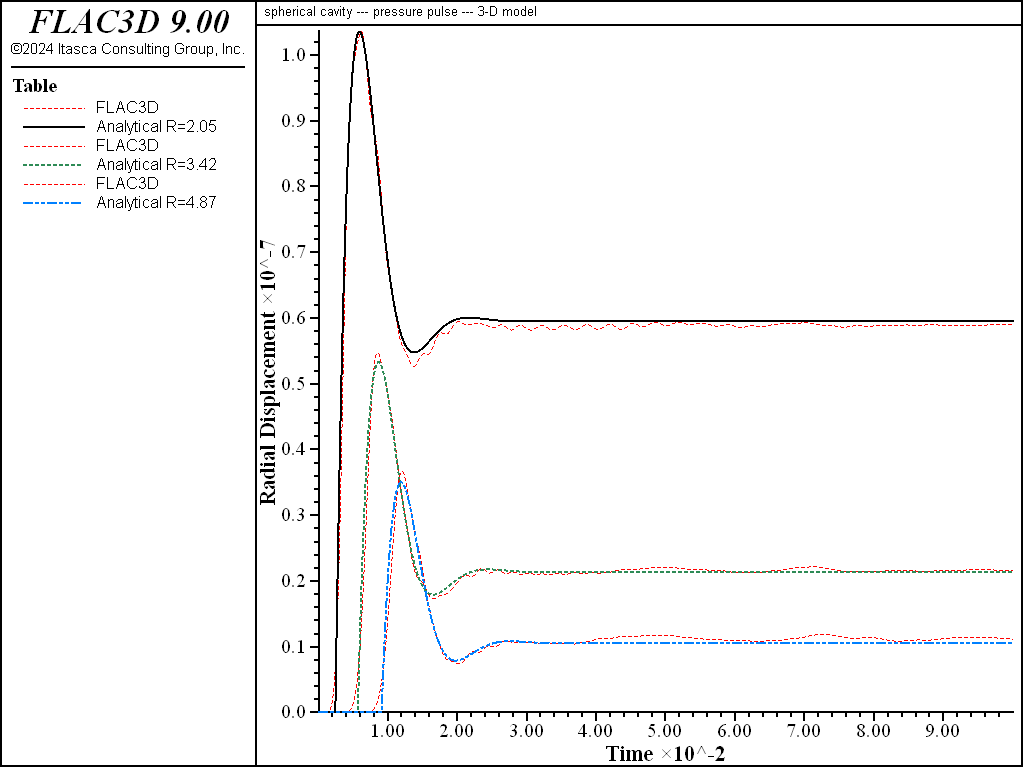
click to enlarge in a new window

Figure 4: Radial displacement histories at r = 2.05a, 3.42a, and 4.87a (3D case).

References

Blake, F. G. “Spherical Wave Propagation in Solid Media,” J. Acous. Soc. Am., 24(2), 211-215 (1952).

Data Files

SphericalPulse1D.dat

model new
model large-strain off
model title "spherical cavity --- pressure pulse --- 1-D model"
model configure dynamic
;--- Generate zones, representing a 1D column on the sphere.
zone create brick  point 0 (10,0,0)           point 1 (100,0,0)          ...
                   point 3 (9.8769,1.5643,0)  point 6 (98.770,15.645,0)  ...
                   point 2 (9.8769,0,-1.5643) point 4 (98.770,0,-15.645) ...
                   point 5 (9.7552,1.5643,-1.5451) ...
                   point 7 (97.555,15.645,-15.450) ...
                   size 30 1 1  ratio 1.01 1 1
;--- Assign constitutive model and properties
zone cmodel assign elastic
zone property shear=1e10 bulk=1.665e10 density=1675
;--- Name the boundary faces
zone face skin
;--- Apply boundary conditions
zone face apply velocity-normal 0 range group 'South' or 'North' or 'Top' or 'Bottom'
zone face apply stress-normal -1000  range group 'West'
zone face apply quiet                range group 'East'
;--- Set damping
zone dynamic damping rayleigh 0.01 50 stiffness
;---Take some histories
history interval 5
model history name='time' dynamic time-total
zone history name='xd1' displacement-x position (20.5,0,0)
zone history name='xd2' displacement-x position (34.2,0,0)
zone history name='xd3' displacement-x position (48.7,0,0)
;--- Run model for 0.1 seconds, then save
model solve time-total=0.1
model save 'SphericalPulse1D'

SphericalPulse3D.dat

model new
model large-strain off
fish automatic-create off
model title 'spherical cavity --- pressure pulse --- 3-D model'
model configure dynamic
;--- Create zones, in a 1/8 brick
zone create radial-brick edge 100 size 16,16,16,30 ...
                         ratio 1 1 1 1.01 dimension 10,10,10
;--- A FISH function is used to convert from a cube to a sphere
fish define make_sphere
    ; Loop over all GPs and remap their coordinates:
    loop foreach local p_gp gp.list 
        local p = gp.pos(p_gp)
        local dist = math.mag(p)
        local k = 10.0/dist
        local a = p * k
        local maxp = math.max(p->x,math.max(p->y,p->z))
        k = 100.0/maxp
        local b = p * k
        local u = (maxp-10.0)/90.0
        gp.pos(p_gp) = a + (b-a)*u
    end_loop
end
[make_sphere]
;--- Assign constitutive model and properties
zone cmodel assign elastic
zone property shear=1e10 bulk=1.665e10 density=1675
;--- Name boundary faces
zone face skin
;--- Assign boundary conditions
zone face apply velocity-normal 0 range group 'West' or 'South' or 'Bottom2'
zone face apply quiet range group 'East' or 'North' or 'Top'
zone face apply stress-normal -1000 range group 'Bottom1
;--- Assign damping
zone dynamic damping rayleigh 0.01 50 stiffness
;--- Take some histories
history interval 5
model history name='time' dynamic time-total
zone history name='xd1' displacement-x position (20.5,0,0)
zone history name='xd2' displacement-x position (34.2,0,0)
zone history name='xd3' displacement-x position (48.7,0,0)
;--- Run model for 0.1 seconds, then save
model solve time-total=0.1
model save 'SphericalPulse3D'