`ball generate` command

Syntax

ball generate keyword ... <range>

Primary keywords:

box cubic fish-distribution gauss group hexagonal id number radius tries

Generate non-overlapping balls. The process ceases when the target number of balls are created or when the number of attempts to place balls without overlap is achieved. By default, the ball positions and radii are drawn from uniform distributions throughout the model domain. As a result, the set of balls generated is affected by the state of the random-number generator (see model random). The ball radii can also be drawn from a Gaussian distribution via the gauss keyword. Cubic and hexagonal packings are also supported with the cubic and hexagonal keywords. The optional range is applied to each ball upon generation and, if the ball does not fall within the range, it is not added to the model and does not affect the stopping criteria. This command contrasts with the ball distribute command where balls are distributed without regard for overlap until a target porosity is achieved.

Note

A model domain must be specified prior to ball generation.
While cycling, balls can only be created before cycle point 0 (i.e., when the timestep is calculated).

box fxmin fxmax <fymin fymax <fzmin fzmax >> (`z`-components are 3D ONLY): Ball will fully fall within this box, such that they will not overlap the box faces or edges. By default, the box is the model domain. Following specification of the box extent in the \(x\)-direction, if subsequent extents are omitted, then the latest specified extent is used.

cubic: The ball positions are assigned so that a regular, cubic packing results that entirely fills the specified region. The lowest radius, fradlow, is used for the ball radii so that the ball centroids are 2*fradlow units apart in each axial direction.

fish-distribution s a₁...a_n: The ball radii are drawn from the distribution represented by the FISH function s. Function arguments can be specified as though no function arguments are required. The FISH function must return a floating point value that is the ball radius. A FISH distribution cannot be specified with the cubic, gauss, hexagonal, or radius keywords.

gauss <f >: Specify that the ball radii are chosen from a Gaussian distribution with mean value (fradlow + fradhi)/2 and standard deviation (fradhi - fradlow)/2. The optional f (default 0.1), multiplied by fradlow, constitutes the minimum radius allowed. Cannot be given with the cubic or hexagonal keywords.

group s <slot slot > ...: Specify that generated balls are given group name s at slot slot. If the slot keyword is not specified, then the group name is assigned to the slot Default.

hexagonal: The ball positions are assigned so that a {hexagonal in 2D; face-centered-cubic in 3D} packing results that entirely fills the generation region. The upper radius, fradhi, is used for the ball spacing. The ball radius is chosen from a uniform distribution with minimum radius fradlow and maximum radius fradhi, is used for the ball radii.

id idlow <idhi >: The ID of the first ball generated is set to idlow that, by default, is the next available ID. idhi, if specified, is used to calculate the number of balls to generate. Ball IDs are chosen sequentially. The specification of idhi does not affect the cubic or hexagonal behaviors.

number i: Specify the number of balls to be generated. The specification of i does not affect the cubic nor hexagonal behaviors.

radius fradlow <fradhi >: Specify the radius range to be used during generation. If fradhi is not specified then fradhi = fradlow. By default, fradhi = fradlow = 1.0. Cannot be given with the fish-distribution keyword.

tries i: Number of tries to fill the specified region with the number of balls. By default, i = 20,000.

Usage Example

The ball generate command is one of the three commands that can be used to create balls. Alternative commands are ball distribute and ball create. As discussed in the command description, ball generate will generate non-overlapping balls within a given range up to a specified number, or until a specified number of attempts to position a new ball is reached.

Simple Example

The following code calls ball generate twice: the first time to generate 100 balls with radii ranging from 0.5 to 0.7 in the left-hand side of the domain, and the second time to generate 100 balls with radii ranging from 1.0 to 1.4 on the right-hand side of the domain. Note that the target number of large balls is not met—the command stopped after the default number of tries (20,000) has been reached.

; setup model domain and CMAT
model domain extent -10.0 10.0 condition periodic
contact cmat default model linear method deformability emod 1e6 ...
                                         kratio 1.25 property fric 0.25
; generate balls
model random 10001 ; set the seed of the random number generator
                   ; to ensure repeatability
ball generate radius 0.5 0.7 number 100 box -5.0  0.0 -5.0 5.0 
ball generate radius 1.0 1.4 number 100 box  0.0  5.0 -5.0 5.0 

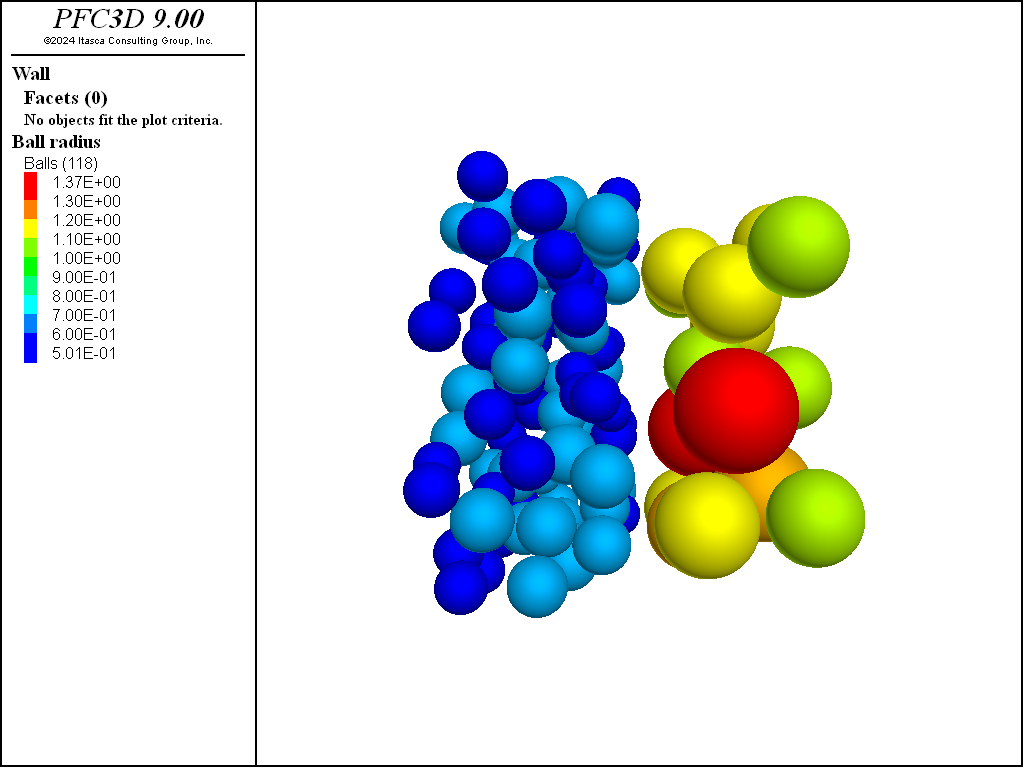
../../../../../../_images/p3d-cmd-ballgenerate1.png — Figure 1: Specimen after 2 executions of the `ball generate` command with the same target number of balls but different radii. Note that generation of large balls stopped before reaching the target number.

The code above also sets the domain extent and the default slots of the CMAT. Additionally, the seed of the random number generator is fixed using the model random command to ensure repeatability.

In order to start integrating the motion of the particles over time, ball density is set, as well as some non-zero local damping coefficient (to remove energy from the system), an enclosing wall is generated, gravity is turned on, and the system is finally solved to a target average ratio of 0.001. The final state is shown in Figure 2, and the corresponding code follows.

model large-strain on
; create a surrounding box, assign density and local damping attributes
wall generate box -6.0 6.0
ball attribute density 1000.0 damp 0.7

; set gravity magnitude and solve
model gravity 10.0
model solve ratio-average 1e-3

../../../../../../_images/p3d-cmd-ballgenerate2.png — Figure 2: System settled in a box under gravity.

Using Built-in Size Distributions

The ball generate command provides uniform and Gaussian distribution functions. The code below exercises both distributions, and the system is shown in Figure 3.

model domain extent -15.0 15.0
model random 10001 

ball generate id 1 200      ...
              radius 0.5 0.6 ...
              box -15.0 -5.0 -5.0 5.0  ...
              range sphere center -10.0 0.0 0.0 radius 5.0

ball generate id 201 400      ...
              radius 0.5 0.6 ...
              gauss          ...
              box  5.0 15.0 -5.0 5.0 ...
              range sphere center 10.0 0.0 0.0 radius 5.0

../../../../../../_images/p3d-cmd-ballgenerate3.png — Figure 3: Two set of balls produced with a uniform (left) and a Gaussian (right) particle size distribution.

The balls on the left have been generated using a uniform size distribution, whereas a Gaussian distribution has been used to generate the balls on the right. Note the usage of the id keyword, for which the specified IDs must not be repeated. Also, note that both sets of balls have been generated in a spherical range.

To evaluate the particle-size distributions that have been produced, the measure logic may be used. The code below creates two measurement spheres encompassing each set of balls and computes their cumulative volume distribution ratio. The result is exported to a table, which are shown in Figure 4

measure create id 1                 ...
               position-x -10.0     ...
               position-y 0.0       ...
               position-z 0.0       ...
               radius 5.0           ...
               bins 20 0.75 1.5
                
measure create id 2                 ...
               position-x  10.0     ... 
               position-y 0.0       ...
               position-z 0.0       ...
               radius 5.0           ...
               bins 20 0.75 1.5

measure dump id 1 table 'uniform'
measure dump id 2 table 'gauss'

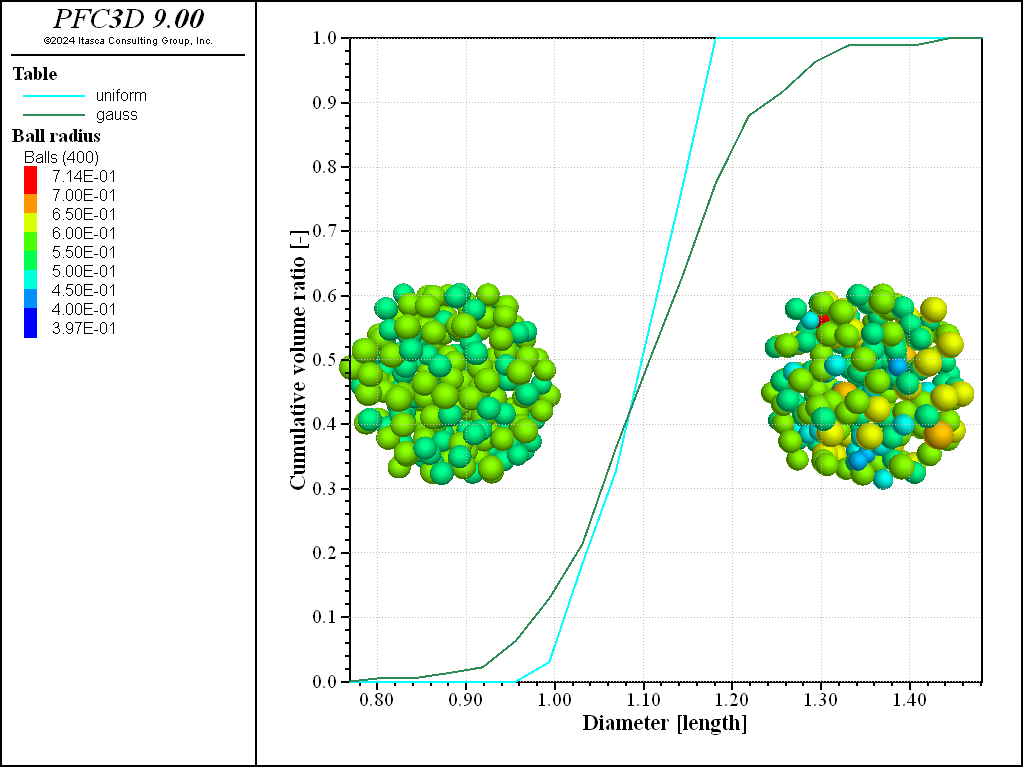
../../../../../../_images/p3d-cmd-ballgenerate4.png — Figure 4: Measured cumulative volume ratio for each set of balls.

Using a Custom Size Distribution

The fish-distribution keyword may also be used to generate balls according to a user-defined distribution law, as illustrated below, where a U-quadratic cumulative distribution function is used with radii ranging from 0.5 to 1.0. The system is shown in Figure 5 along with the cumulative volume distribution function computed with a measurement sphere.

model random 10001
model domain extent -25.0 25.0

fish define mydist(rmin,rmax)
  p = math.random.uniform
  a = 12.0/(rmax-rmin)^3
  b = 0.5*(rmin+rmax)
  temp = (3.0*p/a) - (b-rmin)^3
  if temp >= 0.0 then
    mydist = b + temp^(1.0/3.0)
  else
    mydist = b - (-1.0*temp)^(1.0/3.0)
  endif  
end

ball generate id 1 10000      ...
              fish-distribution mydist 0.5 1.0
              
measure create id 1                 ...
               position-x  0.0      ...
               position-y  0.0      ...
               position-z  0.0      ...
               radius 25.0          ...
               bins 100 1.0 2.0
                
measure dump id 1 table 'size_dist'

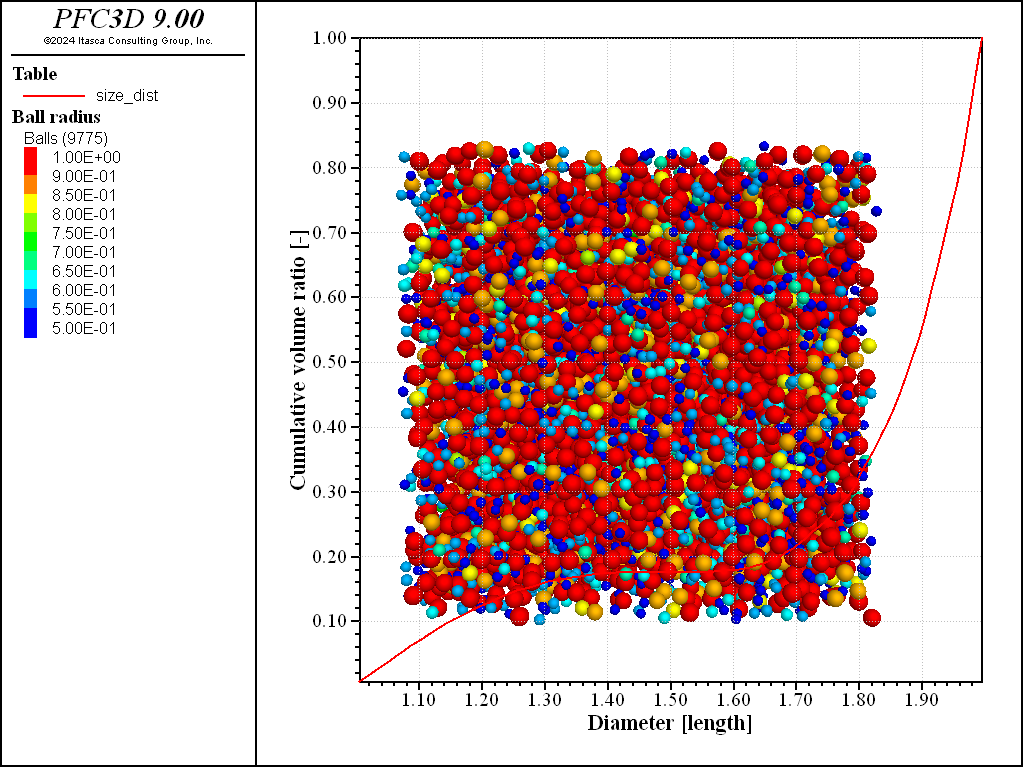
../../../../../../_images/p3d-cmd-ballgenerate5.png — Figure 5: Set of balls generated using a U-quadratic distribution function with radii ranging from 0.5 to 1.0.

ball generate command

`ball generate` command