Smooth-Joint Model

The smooth-joint model can be installed at ball-ball contacts and is referred to in commands and FISH by the name smoothjoint.

Introduction

The smooth-joint model simulates the behavior of a planar interface with dilation regardless of the local particle contact orientations along the interface. The behavior of a frictional or bonded joint can be modeled by assigning smooth-joint models to all contacts between particles that lie on opposite sides of the joint.

Behavior Summary

The smooth-joint model provides the macroscopic behavior of a linear elastic and either bonded or frictional interface with dilation (see Figure 1). The behavior of the bonded interface is linear elastic until the strength limit is exceeded and the bond breaks, making the interface unbonded; the behavior of an unbonded interface is linear elastic and frictional with dilation, with slip accommodated by imposing a Coulomb limit on the shear force. The interface does not resist relative rotation ($\mathbf{M_{c}} \equiv 0$). The force is updated as described in the force-displacement law below.

Figure 1: Behavior and rheological components of the smooth-joint model.

Activity-Deletion Criteria

If in small-strain mode ($S_l = \rm false$), a contact with the smooth-joint model is always active. In this mode, the contact will never be deleted. If in large-strain mode ($S_l = \rm true$), a contact with the smooth-joint model is active if the contact is bonded or if the contact gap is negative (i.e., the two pieces are overlapping).

Kinematic Variables

A typical smooth-joint contact is shown in Figure 2. The joint geometry consists of a planar interface separating two surfaces (denoted as surface 1 and surface 2). The interface orientation is defined by the unit-normal vector ${\bf \hat n_j}$, and surface 2 is defined such that ${\bf \hat n_j}$ points into surface 2. The unit normal is defined as:

(1) $$\begin{split}\begin{array}{l} {{\bf \hat n_j} = ({\rm sin} (\theta_p) , {\rm cos} (\theta_p)) \hspace {43mm} (2D)} \\[3mm] {{\bf \hat n_j} = ({\rm sin} (\theta_p) {\rm sin} (\theta_d), {\rm sin} (\theta_p) {\rm cos} (\theta_d), {\rm cos} (\theta_p)) \quad (3D)} \end{array}\end{split}$$

where $\theta_p$ is the dip angle and $\theta_d$ the dip direction.

Joint orientation is fixed with respect to the global axes, and can only be changed by modifying the dip angle or dip direction. Whenever the joint orientation is changed (or is set initially), the two contacting entities (called piece 1 and piece 2) are associated with the appropriate joint surfaces. The contact unit-normal vector, ${\bf \hat n_c}$, is directed from the center of piece 1 to the center of piece 2. The dot product of ${\bf \hat n_c}$ and ${\bf \hat n_j}$ is used to determine in which surface each piece lies, such that piece 2 lies in surface 2 if and only if ${\bf \hat n_c \cdot \hat n_j} \geq 0$.

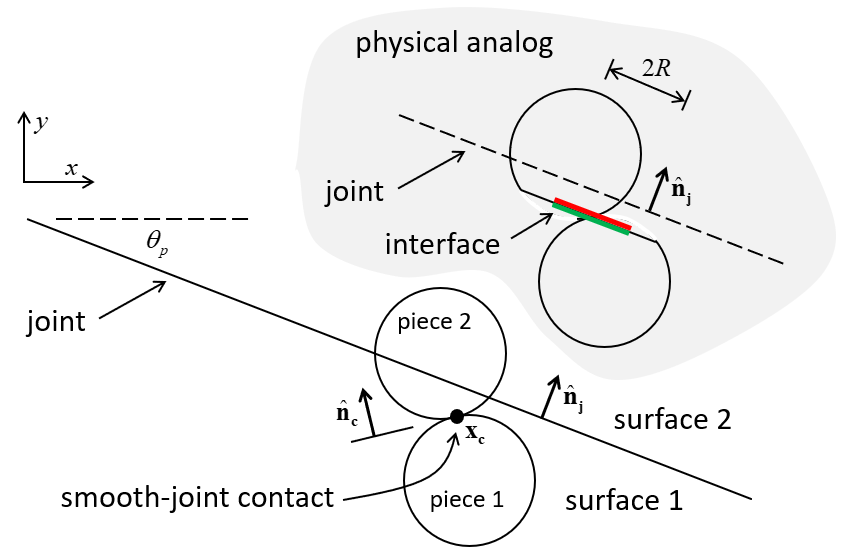
Figure 2: Joint and smooth-joint contact.

A smooth joint can be envisioned as a set of elastic springs uniformly distributed over a circular cross-section, centered at the contact point and oriented parallel with the joint plane. The area of the smooth-joint cross-section is given by:

(2) $$\begin{split} \begin{array}{l} {A = \pi R^2} \\[3mm] {{\rm with} \qquad R = \lambda {\rm min} (R^{(1)}, R^{(2)})} \end{array}\end{split}$$

where $R^{(1)}$ and $R^{(2)}$ are the piece radii.

Force-Displacement Law

As the smooth-joint orientation is not aligned with the contact normal, the relative displacement increment is resolved into joint normal and shear directions:

(3) $$\Delta {{\pmb δ}} =\Delta \stackrel{\frown}{{\delta_n}} {\kern 1pt} {\bf \hat n_j} +\Delta \stackrel{\frown}{{\pmb δ}_\mathbf{s}}$$

The accumulated normal and shear displacements are updated as:

(4) $$\begin{split}\stackrel{\frown}{{\delta_n}} \enspace = \enspace \stackrel{\frown}{{\delta_n}} - \Delta \stackrel{\frown}{{\delta_n}} \\ \stackrel{\frown}{{\pmb δ}_\mathbf{s}} \enspace = \enspace \stackrel{\frown}{{\pmb δ}_\mathbf{s}} + \Delta \stackrel{\frown}{{\pmb δ}_\mathbf{s}}\end{split}$$

The elastic portions of the normal ($\Delta \stackrel{\frown}{{\delta_n}^e}$) and shear ($\Delta \stackrel{\frown}{{{\pmb δ}_\mathbf{s}}^e}$) displacement increments are determined based on the value of the gap ($g_i$ where $g_i=0$ when the smooth joint is created). If bonded, then the entire displacement increment is elastic; if not bonded, then only the portion of the displacement increment that occurs while $g_i<0$ is elastic.

The force-displacement law for the smooth-joint model updates the contact force:

(5) $$\mathbf{F_{c}} =\mathbf{F}$$

where $\mathbf{F}$ is the smooth-joint force. The force is resolved into normal and shear forces:

(6) $$\mathbf{F} =-F_{n} {\kern 1pt} {\bf \hat n_j} +\mathbf{F_{s}}$$

where $F_n>0$ is tension.

The force-displacement law consists of the following steps (see Figure 3 and Figure 4):

1. Update the normal force:

   (7) $$F_n = \left(F_n \right)_o + {k_n} A \Delta \stackrel{\frown}{{\delta_n}^e}$$

   where $\left(F_n \right)_o$ is the smooth joint normal force at the beginning of the timestep and $A$ is the bond cross-sectional area.

2. Calculate a trial shear force:

   (8) $$\mathbf{F_{s}}^{*} =\left(\mathbf{F_{s}} \right)_{o} -k_{s} A \Delta \stackrel{\frown}{{\pmb{δ}_\mathbf{s}}^e}$$

   where $\left(\mathbf{F_{s}} \right)_{o}$ is the shear force at the beginning of the timestep.

   The frictional shear-strength limit is also computed:

   (9) $$F_{s}^{\mu } =-\mu F_{n}.$$

3. The forces, slip state, and bonding state are updated based on the bonding status.

   • If the smooth-joint model is unbonded ($S_j<3$), the shear force is updated:

     (10) $$\begin{split}\mathbf{F_{s}} =\left\{\begin{array}{l} {\qquad \mathbf{F_{s}}^{*} ,\qquad \left\| \mathbf{F_{s}}^{*} \right\| \le F_{s}^{\mu } } \\ {\qquad F_{s}^{\mu } \left({\mathbf{F_{s}}^{*} \mathord{\left/ {\vphantom {\mathbf{F_{s}}^{*} \left\| F_{s}^{*} \right\| }} \right. } \left\| \mathbf{F_{s}}^{*} \right\| } \right),\qquad {\rm otherwise.}} \end{array}\right.\end{split}$$

     The slip state is updated:

     (11) $$\begin{split}s=\left\{\begin{array}{l} {\qquad {\rm true},\qquad \left\| \mathbf{F_{s}} \right\| =F_{s}^{\mu } } \\ {\qquad {\rm false},\qquad {\rm otherwise.}} \end{array}\right.\end{split}$$

     If the slip state is true, then the contact is sliding. Whenever the slip states changes, the slip_change callback event occurs. While slipping, shear displacements produce an increase in normal force due to dilation:

     (12) $$F_n = \left(F_n \right)_o + \left[ \stackrel{\frown}{{\delta_\mathbf{s}}^*} {\rm tan} \psi \right] {{k_n}} {{A}} = \left(F_n \right)_o + \left({{\left\| \mathbf{F_{s}}^{*} \right\| - F_{s}^{\mu }} \over {{k_s}}} \right) {k_n} {\rm tan} \psi$$

     where $\mu$ is the friction coefficient and $\psi$ is the dilation angle.

   • If the smooth-joint model is bonded ($S_j=3$), one updates the bonding status:

     (13) $$\begin{split} S_j=\left\{\begin{array}{l} {\qquad 1,\qquad F_n \ge \sigma_c A \qquad (\rm{broken} \enspace \rm{in} \enspace \rm{tension})} \\ {\qquad 2, \qquad \left\| \mathbf{F_s}^* \right\| \ge \tau_c A \qquad (\rm{broken} \enspace \rm{in} \enspace \rm{shear})} \\ {\qquad 3, \qquad {\rm otherwise.}} \end{array}\right.\end{split}$$

     where $\sigma_c$ is the bond normal strength and $\tau_c$ is the bond shear strength ($\tau_c = c - \left( {{F_n}} \over {{A}} \right){\rm tan} \phi$). The following conditions are applied in each case:

     • If the bond has broken in tension ($S_j=1$), the normal and shear forces are reset:

       (14) $$F_n = \left\| \mathbf{F_s} \right\| = 0.$$

     • If the bond has broken in shear ($S_j=2$) and the bond is in tension, the normal and shear forces are reset as in Equation (14). If the bond is not in tension, the shear force is limited by Equation (10) but no dilation can occur. The slip state is updated as in Equation (11).

     • If the bond remains intact ($S_j=3$), the shear force is set to the trial shear force:

       (15) $$\mathbf{F_s} = \mathbf{F_s}^*.$$

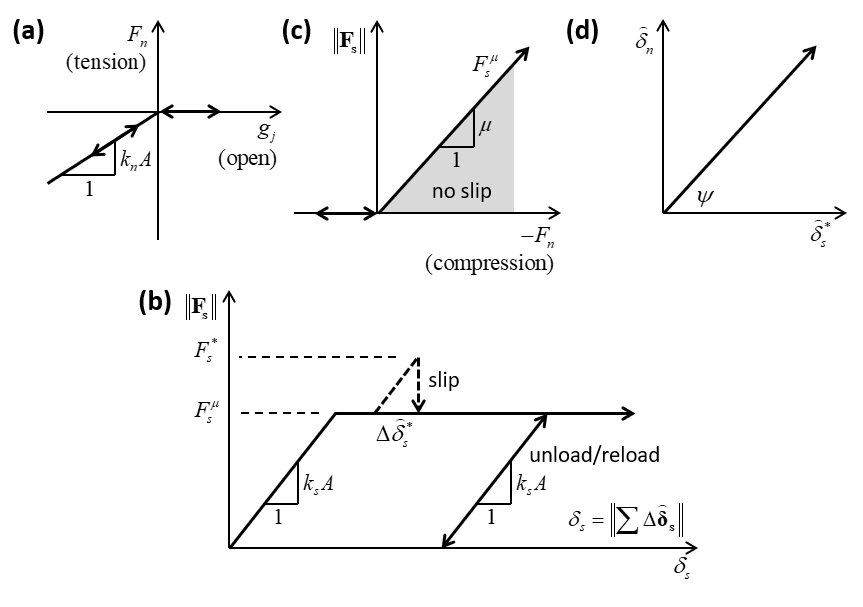
Figure 3: Force-displacement law for an unbonded joint: (a) normal force versus normal displacement; (b) shear force versus shear displacement; (c) strength envelope; and (d) normal displacement versus shear displacement during sliding.

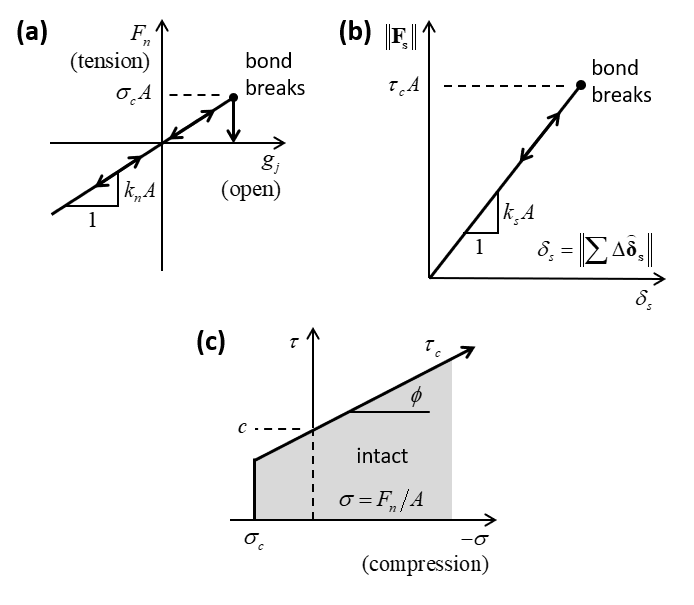
Figure 4: Force-displacement law for a bonded joint: (a) normal force versus normal displacement; (b) shear force versus shear displacement; and (c) strength envelope.

Energy Partitions

The smooth-joint model provides two energy partitions:

• strain energy, $E_{k}$, stored in the linear springs; and

• slip energy, $E_{\mu }$, defined as the total energy dissipated by frictional slip.

If energy tracking is activated, these energy partitions are updated as follows:

1. Update the strain energy:

   (16) $${\rm E} _{k} =\frac{1}{2} \left(\frac{\left(F_{n} \right)^{2} }{k_{n} } +\frac{\left\| \mathbf{F_{s}} \right\| ^{2} }{k_{s} } \right)$$

2. Update the slip energy:

   (17) $$\begin{split}\begin{array}{l} {E_{\mu } :=E_{\mu } +{\tfrac{1}{2}} \left(\left(\mathbf{F_{s}} \right)_{o} +\mathbf{F_{s}} \right)\cdot \Delta \pmb{δ} _\mathbf{s}^{\mu } } \\ [3mm] {{\rm with}\qquad \Delta \pmb{δ} _\mathbf{s}^{\mu } =\Delta \pmb{δ} _\mathbf{s} -\Delta \pmb{δ} _\mathbf{s}^{e} =\Delta \pmb{δ} _\mathbf{s} -\left(\frac{\mathbf{F_{s}} -\left(\mathbf{F_{s}} \right)_{o} }{k_{s} } \right)} \end{array}\end{split}$$

   where $\left(\mathbf{F_{s}} \right)_{o}$ is the shear force at the beginning of the timestep, and the relative shear-displacement increment of this equation of the “Contact Resolution” section has been decomposed into an elastic $\left(\Delta \pmb{δ} _\mathbf{s}^{e} \right)$ and a slip $\left(\Delta \pmb{δ} _\mathbf{s}^{\mu } \right)$ component. The dot product of the slip component and the average shear force occurring during the timestep gives the increment of slip energy.

Additional information, including the keywords by which these partitions are referred to in commands and FISH, is provided in the table below.

Table 1: Smooth-Joint Contact Model Energies

Name	Symbol	Description	Range	Accumulated
energy‑strain	$E_{k}$	Strain energy	$[0.0,+\infty)$	NO
energy‑slip	$E_{\mu}$	Total energy dissipated by slip	$[0.0,+\infty)$	YES

Properties

The properties defined by the smooth-joint contact model are listed in the table below as a concise reference; see the “Contact Properties” section for a description of the information in the table columns. The mapping from the surface inheritable properties to the contact model properties is also discussed below.

Table 2: Smooth-Joint Model Properties

Keyword	Symbol	Description	Type	Range	Default	Modifiable	Inheritable
smoothjoint		Model name
sj_kn	$k_n$	Normal stiffness per unit area [force/volume]	FLT	$[0.0,+\infty)$	0.0	YES	YES
sj_ks	$k_s$	Shear stiffness per unit area [force/volume]	FLT	$[0.0,+\infty)$	0.0	YES	YES
sj_fric	$\mu$	Friction coefficient [-]	FLT	$[0.0,+\infty)$	0.0	YES	YES
sj_da	$\psi$	Dilation angle [degrees]	FLT	$[0.0,+\infty)$	0.0	YES	NO
sj_state	$S_j$	Joint bond state [-]	INT	{0;1;2;3}	0	YES	NO
		$\;\;\;\;\;\;\begin{cases} \mbox{0: unbonded} \\ \mbox{1: unbonded \& broke in tension} \\ \mbox{2: unbonded \& broke in shear} \\ \mbox{3: bonded} \end{cases}$
sj_large	$S_l$	Large strain flag [-]	BOOL	{false,true}	false	YES	NO
sj_ten	${\sigma}_c$	Tensile strength [stress]	FLT	$[0.0,+\infty)$	0.0	YES	NO
sj_coh	$c$	Cohesion	FLT	$[0.0,+\infty)$	0.0	YES	NO
sj_fa	$\phi$	Joint friction angle [degrees]	FLT	$[0.0,+\infty)$	0.0	YES	NO
sj_shear	${\tau}_c$	Shear strength [stress]	FLT	$[0.0,+\infty)$	0.0	NO	NO
sj_rmul	$\lambda$	Joint radius multiplier [-]	FLT	$[0.0,+\infty)$	1.0	YES	NO
sj_radius	$R$	Joint radius [length]	FLT	$[0.0,+\infty)$	N/A	NO	N/A
sj_area	$A$	Joint area [surface]	FLT	$[0.0,+\infty)$	N/A	NO	N/A
sj_slip	$s$	Slip state [-]	BOOL	{false,true}	false	NO	N/A
sj_gap	$g_j$	Joint gap [length]	FLT	$\mathbb{R}$	0.0	YES	NO
sj_unorm	$\mathbf{\hat{n}_j}$	Joint unit normal [force]	VEC	$\mathbb{R}^3$	$\mathbf{0}$	NO	NO
sj_un	$\stackrel{\frown}{{\delta_n}}$	Normal displacement [length]	FLT	$\mathbb{R}$	0.0	NO	N/A
sj_us	$\stackrel{\frown}{{\pmb{δ}_\mathbf{s}}}$	Shear displacement [length]	VEC	$\mathbb{R}^3$	$\mathbf{0}$	NO	N/A
dip	$\theta_p$	Joint dip [degrees]	FLT	[0.0,360.0]	0.0	YES	NO
ddir (3D)	$\theta_d$	Joint dip direction [degrees]	FLT	[0.0,180.0]	0.0	YES	NO
sj_fn	$F_n$	Normal force magnitude [force]	FLT	$\mathbb{R}$	0.0	YES	NO
sj_fs	$\mathbf{F_s}$	Shear force vector [force]	VEC	$\mathbb{R}^3$	$\mathbf{0}$	YES	NO

Surface Property Inheritance

The linear stiffness per unit area, $k_n$ and $k_s$, and the friction coefficient, $\mu$, may be inherited from the contacting pieces. Remember that for a property to be inherited, the inheritance flag for this property must be set to true, and both contacting pieces must hold a property with this name.

The stiffness are inherited assuming that both pieces’ stiffness act in series:

(18) $$\begin{split}\frac{1}{{k}_n} = \frac{1}{{k}^{(1)}_n} + \frac{1}{{k}^{(2)}_n} \\ \frac{1}{{k}_s} = \frac{1}{{k}^{(1)}_s} + \frac{1}{{k}^{(2)}_s}\end{split}$$

where (1) and (2) denote the properties of piece 1 and 2, respectively. The friction coefficient is inherited using the minimum friction coefficient:

(19) $$\mu = \min(\mu^{(1)},\mu^{(2)})$$

Methods

Table 3: Smooth-Joint Model Methods

Method	Arguments	Symbol	Type	Range	Default	Description
sj_setforce	N/A					Set the force
bond						Bond the joint if $g_j \in G$
	gap	$\mathbb{G}$	VEC2	$\mathbb{R}^2$	$(-\infty,0]$	Gap interval
unbond						Unbond the joint if $g_j \in G$
	gap	$G$	VEC2	$\mathbb{R}^2$	$(-\infty,0]$	Gap interval

sj_setforce

Set the smooth-joint normal force ($F_n$) from the current contact force:

(20) $$F_n = \mathbf{F_c} \cdot \mathbf{\hat{n}_j}.$$

Bond

Create a smooth-joint bond ($S_j=3$) by bonding the interface if the contact gap between the pieces is within the bonding-gap interval. If no gap is specified, then the contact is bonded if the pieces overlap. A single value can be specified with the gap keyword corresponding to the maximum gap. One can ensure the existence of contacts between all pieces with a contact gap less than a specified bonding gap ($g_{b}$) by specifying $g_{b}$ as the proximity in the contact cmat default command of the Contact Model Assignment Table (CMAT).

Unbond

Remove a smooth-joint bond by unbonding ($S_j=0$) the interface if the contact gap between the pieces is within the bonding-gap interval. If no gap is specified, then the contact is unbonded if the pieces overlap. A single value can be specified with the gap keyword corresponding to the maximum gap. If the interface becomes unbonded, then the bond state becomes unbonded. The smooth-joint force is unaffected and will be updated during the next cycle.

Callback Events

Table 4: Smooth-Joint Model Callback Events

Event	Array slot	Value Type	Range	Description
contact_activated				Contact becomes active
	1	C_PNT	N/A	Contact pointer
slip_change				Slip state has changed
	1	C_PNT	N/A	Contact pointer
	2	INT	{0;1}	Slip change mode
			{0;1}	$\;\;\;\;\;\;\begin{cases} \mbox{0: slip has initiated} \\ \mbox{1: slip has ended} \end{cases}$
bond_break				Bond has broken
	1	C_PNT	N/A	Contact pointer
	2	INT	{1;2}	Failure mode
				$\;\;\;\;\;\;\begin{cases} \mbox{1: failed in tension} \\ \mbox{2: failed in shear} \end{cases}$
	3	FLT	$[0.0,+\infty)$	Failure strength [stress] (tension or shear, according to the failure mode)

Usage and Verification Examples

The smooth-joint contact model is demonstrated in the “Slip on a Fault” tutorial.

Model Summary

An alphabetical list of the smoothjoint model methods is given here. An alphabetical list of the smoothjoint model properties is given here.

• Smooth-Joint Model Methods
• Smoothjoint Model Properties