Zone
Orientation of Nodes and Faces within a Zone
A zone is a closed geometric domain, with nodes at the vertices and faces forming the boundary of the zone (surfaces in 3D or edges in 2D).
Zones in 3D
The relative orientation of the nodes and faces is shown in the figure below for the basic zone types: brick, wedge, pyramid, degenerate brick and tetrahedron (see zone create for full list). Each face has vertices; these vertices are also identified in the figure. Several FLAC and FISH commands (e.g., zone attach) refer to this orientation.
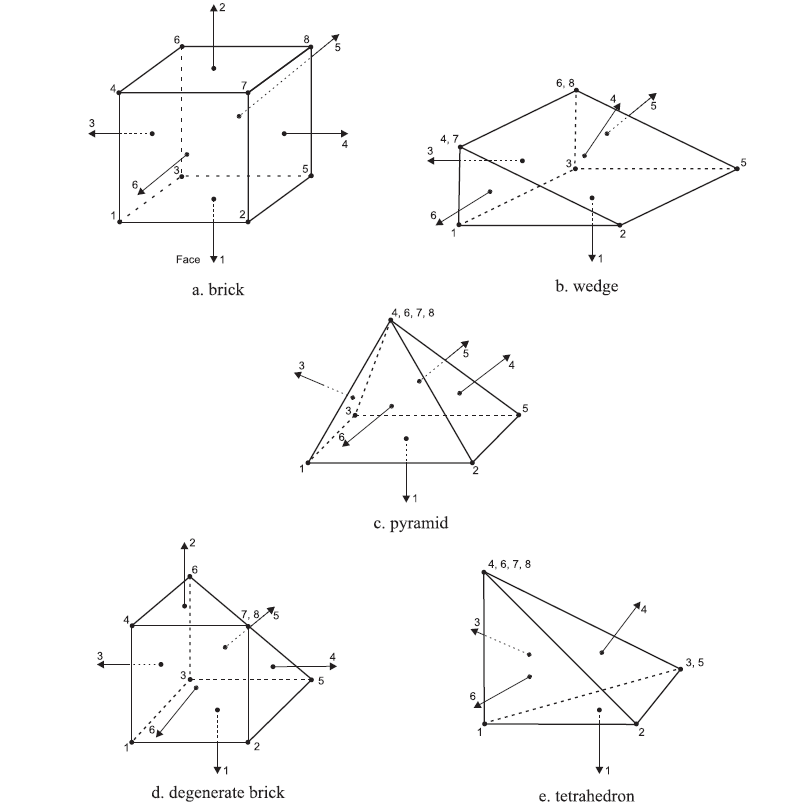
Figure 1: 3D zone geometry.
Zones in 2D
The relative orientation of the nodes and faces is shown in the figure below for the basic zone types: quadrilateral and triangle (see zone create2d for full list). Each face (represented by an edge in 2D) has two connected vertices; these vertices are also identified in the figure. Several FLAC and FISH commands (e.g., zone attach) refer to this orientation.
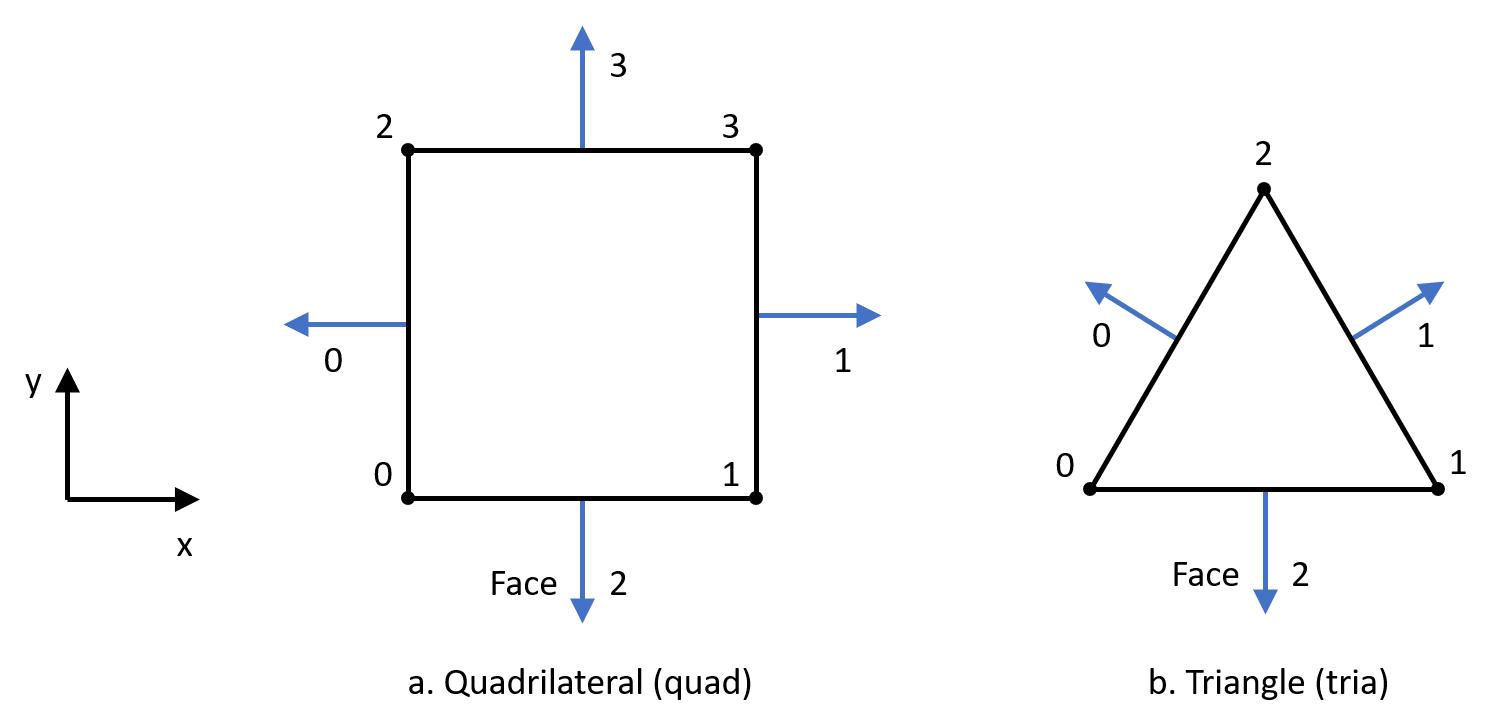
Figure 2: 2D zone geometry.
Condition Measure of Zones
A zone condition number is a measure of how badly deformed a zone is. Several basic measures are included, and the condition number is taken as their minimum to characterize the worst case. The range of a zone condition number is between 0 and 1. The larger the zone number is, the better the zone geometry is. For detailed information about how zone condition number is calculated, refer to zone geometry test.
Zone Field Data Names
In FLAC, the FISH zone field data functions allow the user to make queries about the values of a model variable at arbitrary locations in space. This includes zone-based information as well as gridpoint-based information. The FISH functions in this section are state-based. Some of them set the particular data type (and the methods and properties used to get that data), while others retrieve the data once these values have been set.
By default, queries operate as quickly as possible for individual calls. If many (hundreds or more) points of data are to be queried, you can initialize the system to optimize multiple calls. This makes it unnecessary to calculate data more than once in a given zone or gridpoint. As an example, here is a FISH fragment that queries for the gridpoint-based value \(x\)-displacement at a single location in space:
zone.field.name = 'displacement-x'
local result = zone.field.get(vector(3.5,4.3,6.7)) ; for FLAC3D
local result = zone.field.get(vector(3.5,6.7)) ; for FLAC2D
Here is a FISH fragment that performs many queries on a line in space, on the zone-based values of horizontal stress:
array dataset(100)
zone.field.name = 'stress-xx'
zone.field.method.name = ’poly’ ; Use polynomial fit extrapolation
zone.field.init
loop ii (1,100)
local xp = 5.0 + float(ii)/10.0
dataset(ii) = zone.field.get(3.5,4.3,xp) ; for FLAC3D
end_loop
zone.field.reset
The available zone field data names are described in the table below. Note that these are the same values available under zone history, for example.
Zone Field Data Names
Name |
Description |
|---|---|
acceleration |
acceleration magnitude at the gridpoint (only available if |
acceleration-x |
\(x\)-acceleration at the gridpoint (only available if |
acceleration-y |
\(y\)-acceleration at the gridpoint (only available if |
acceleration-z (3D only) |
\(z\)-acceleration at the gridpoint (only available if |
condition |
a measure of how badly deformed a zone is |
density |
the density of the zone |
displacement |
displacement magnitude at the gridpoint |
displacement-x |
\(x\)-displacement at the gridpoint |
displacement-y |
\(y\)-displacement at the gridpoint |
displacement-z (3D only) |
\(z\)-displacement at the gridpoint |
extra |
extra variable value. The extra variable index used will default to 1 and can be changed with the |
factor-of-safety |
largest stable factor of safety of a grid point. Calculated during |
pore-pressure |
pore pressure in zone. By default, this will be the grid point pore pressure but the zone average pore pressure can be specified by using the |
property-fluid |
a property of the fluid constitutive model of the zone. The property name must be specified using the |
property |
a property of the mechanical constitutive model of the zone. The property name must be specified using the |
property-thermal |
a property of the thermal constitutive model of the zone. The property name must be specified using the |
ratio-local |
the local unbalanced force ratio at each gridpoint. Like all results, this can be changed to the logarithm of the value by using the |
saturation |
the saturation at the gridpoint (only available if |
strain-increment |
the strain increment tensor of the zone determined by the current displacement field. Use the |
strain-rate |
the rate increment tensor of the zone determined by the current velocity field. Use the |
stress |
the stress tensor of the zone determined by the weighted average of the subzone stresses. Use the |
stress-effective |
the effective stress tensor of the zone determined by the weighted average of the subzone stresses minus the zone averaged pore pressure. Use the |
strength-stress-ratio |
the strength-stress ratio of the zone. Not all constitutive models support this calculation. If unsupported, the value returned will be 10. The value returned is generally held to a maximum of 10. |
temperature |
the temperature at the gridpoints. The |
timestep-dynamic |
the local critical dynamic timestep of that particular gridpoint (only available if |
unbalanced-force |
the unbalanced force magnitude at the gridpoint |
unbalanced-force-x |
\(x\)-unbalanced force at the gridpoint |
unbalanced-force-y |
\(y\)-unbalanced force at the gridpoint |
unbalanced-force-z (3D only) |
\(z\)-unbalanced force at the gridpoint |
velocity |
the velocity magnitude at the gridpoint |
velocity-x |
\(x\)-velocity at the gridpoint |
velocity-y |
\(y\)-velocity at the gridpoint |
velocity-z (3D only) |
\(z\)-velocity at the gridpoint |
Zone Field Quantity Names
The field data names above may return a range of quantities. The options are listed in the following table. The definitions of the field data of a tensor (stress, strain increment, or strain rate) can be found in Stress/Strain Invariants.
Quantity Name |
Description |
|---|---|
intermediate principal stress or strain (increment/rate) |
|
maximum (most positive) value of the principal stress or strain (increment/rate) |
|
mean value defined as the trace of the tensor divided by three |
|
minimum (most negative) value of the principal stress or strain (increment/rate) |
|
norm of stress or strain (increment/rate) |
|
octahedral stress or strain (increment/rate) |
|
maximum shear stress or strain (increment/rate) |
|
distance from the origin to the tensor point in the principal space |
|
trace of the stress or strain (increment/rate) |
|
von Mises measure of the stress or strain (increment/rate) |
|
\(xx\)-component of the stress or strain (increment/rate) |
|
\(xy\)-component of the stress or strain (increment/rate) |
|
\(xz\)-component of the stress or strain (increment/rate) |
|
\(yy\)-component of the stress or strain (increment/rate) |
|
\(yz\)-component of the stress or strain (increment/rate) |
|
\(zz\)-component of the stress or strain (increment/rate) |
Below is a simple example for 3D case:
zone.field.name = 'stress-xx'
; Use polynomial fit extrapolation
zone.field.method.name = 'poly'
; Return stress-xx
global value1 = zone.field.get(10,0,-20)
; Reset the stress quantity to 'von-mises'
zone.field.quantity = 'von-mises'
; Return stress-von-mises
global value2 = zone.field.get(10,0,-20)
or (2D case)
zone.field.name = 'stress-xx'
; Use Inv. Distance Weighting approach
zone.field.method.name = 'inverse-distance-weighting'
; Return stress-xx
global value1 = zone.field.get(10,-20)
; Reset the filed name directly to 'stress-von-mises'
zone.field.name = 'stress-von-mises'
; Return stress-von-mises
global value2 = zone.field.get(10,-20)
Strength-Stress Ratio
The strength-stress ratio (SSR) is calculated in some constitutive models as a local indicator of the current stress state’s proximity to failure. Suppose the current effective minimum and maximum principal stresses are \(\sigma_1\) and \(\sigma_3\). The current Mohr circle is plotted in Figure 3. By keeping \(\sigma_3\) fixed, enlarge the Mohr circle so that it is tangent to the shear failure line; the new minimum effective principal stress is denoted by \(\sigma^{\prime}_1\), and the strength-stress ratio is defined as
It is self-evident that if the stress state is in shear failure, SSR = 1. The upper limit of SSR in FLAC3D is set to 10. If the current stress state is in tension failure, the SSR is set to 0. SSR can be plotted as a zone contour value if it is defined in the constitutive model.
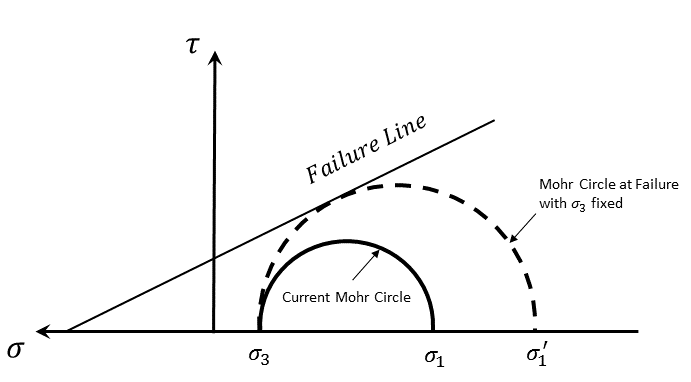
Figure 3: Schematic of strength-stress ratio.
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
