FLAC3D Theory and Background • Constitutive Models

Oedometer Test with Plastic-Hardening Model

Note

To view this project in FLAC3D, use the menu command Help ► Examples…. The project’s main data file is shown at the end of this example.

This section presents the simulation of an oedometer test to reveal the capability of the Plastic-Hardening (PH) model to reproduce the evolution of lateral stress ratio \(K_0 = \sigma_h/\sigma_h\). Three kinds of sands with friction angles of 30, 35, and 40 degrees are used in the simulations of this case (Case 1) and the default consolidation coefficient is calculated as \(K_{nc} = 1 − \sin \phi\). The model properties are listed in Table 1. The properties not listed in the table are using the default values. Initially the model is in equilibrium with isotropic stress state in each zone, \(\sigma_1\) = \(\sigma_2\) = \(\sigma_3\) = −1 kPa.

Table 1: Plastic-Hardening Model Properties

Parameter	Dense	Medium	Loose
\(E^{ref}_{50}\) (kPa)	4.0e4	3.0e4	2.0e4
\(\phi\)	40	35	30
\(\psi\)	10	5	0
\(K_{nc}\) (Case 2)	0.7	0.6	0.5
\(p_{ref}\) (kPa)		100.0
\(m\)		0.5
\(\sigma^{ini}_{1 \sim 3}\) (kPa)		-1.0
\(OCR\)		1.0

The results of stress ratio evolution due to compression in the oedometer tests are shown in Figure 1, and it is seen that they correctly reproduce the expected evolution path. Figure 2 presents vertical oedometer pressure versus vertical strain. The slope of the curves at the specified reference pressure of 100 kPa reproduces the expected oedometer stiffness (as \(E^{ref}_{oed}\) is not provided as part of input, it is assigned to the same as \(E^{ref}_{50}\) by default; see the property section of the PH model).

The test is repeated in Case 2 using predefined values of \(K_{nc}\) = 0.7, 0.6, and 0.5, respectively. The results for \(K_0\) are plotted in Figure 3 and Figure 4 shows variation of vertical oedometer pressure versus axial strain. Again, correct stress paths and oedometer stiffness at the reference vertical pressure are successfully reproduced.

break

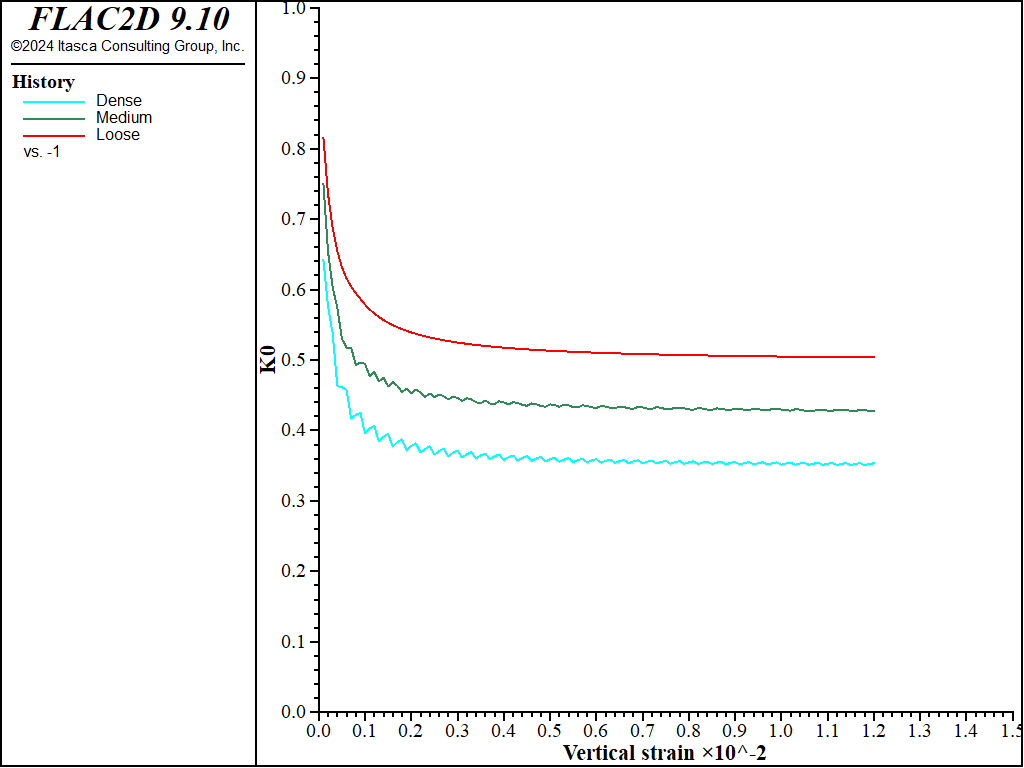
Figure 1: \(K_0\) path calculated from the oedometer test with friction angles of 30, 35, and 40 degrees and default \(K_{nc}\) values.

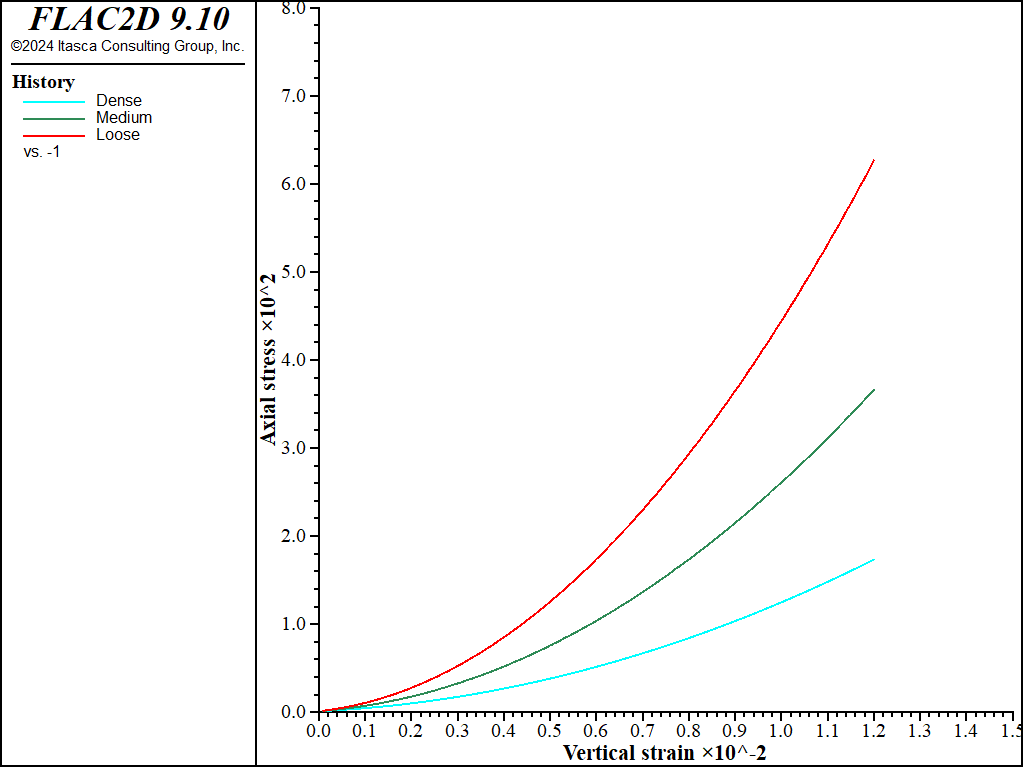
Figure 2: Vertical pressure versus vertical strain from the oedometer test with friction angles of 30, 35, and 40 degrees and default \(K_{nc}\) values.

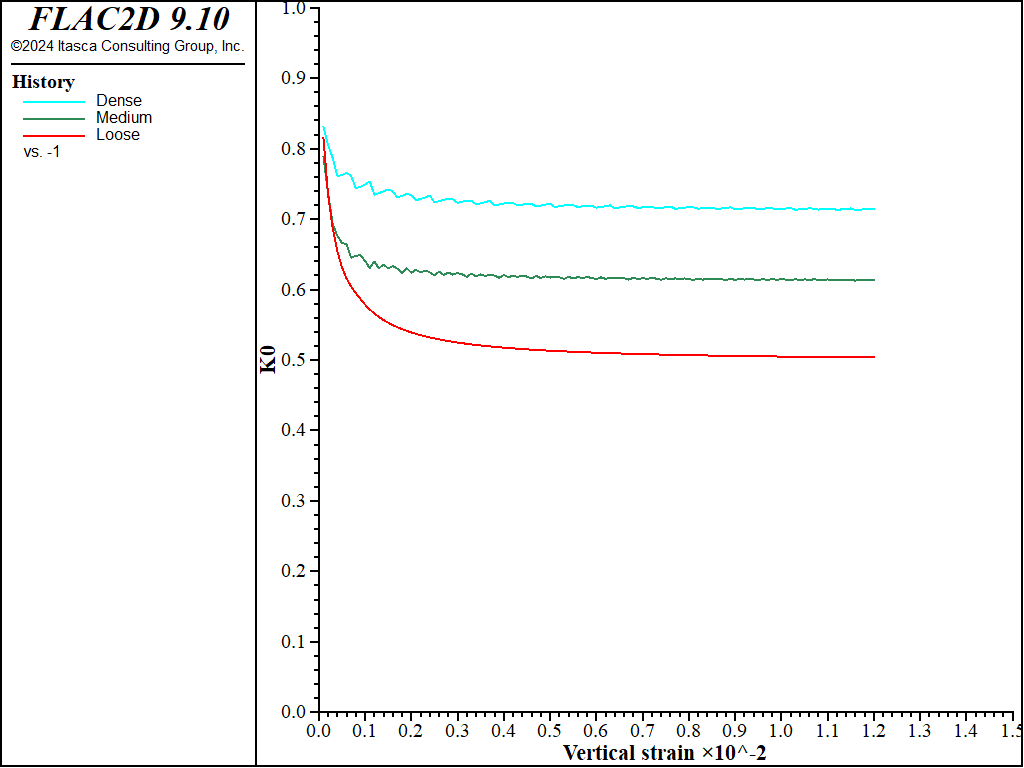
Figure 3: \(K_0\) path calculated from the oedometer test with friction angles of 30, 35, and 40 degrees and specified \(K_{nc}\) values.

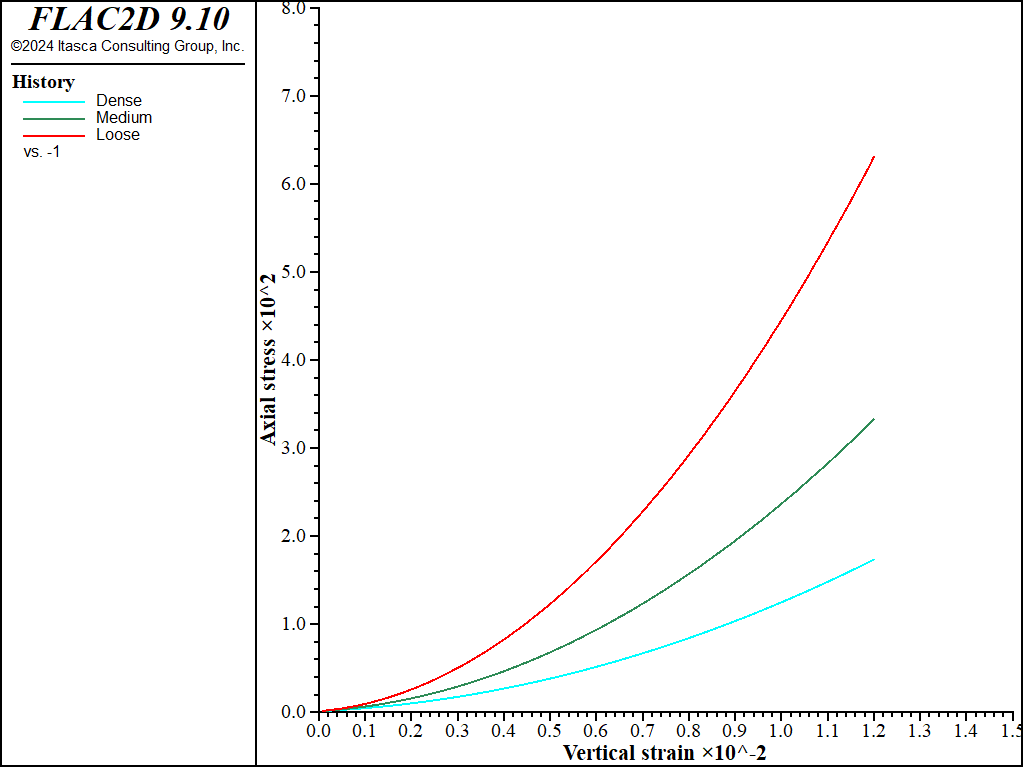
Figure 4: Vertical pressure versus vertical strain from the oedometer test with friction angles of 30, 35, and 40 degrees and specified \(K_{nc}\) values.

Data File

OedometerPlasticHardening.dat

model large-strain off
zone create quadrilateral size 1 5
zone cmodel assign plastic-hardening
zone property density 1000 pressure-reference=100. exponent=0.5 ...
          over-consolidation-ratio=1.0 factor-cut 0.01
zone property stress-1-effective=-1 stress-2-effective=-1 stress-3-effective=-1
zone property stiffness-50-reference=4e4 friction=40. dilation=10. ... 
          coefficient-normally-consolidation=[Knc1] range id 1
zone property stiffness-50-reference=3e4 friction=35. dilation= 5. ... 
          coefficient-normally-consolidation=[Knc2] range id 3
zone property stiffness-50-reference=2e4 friction=30. dilation= 0. ... 
          coefficient-normally-consolidation=[Knc3] range id 5
zone null range id-list 2 4
;
zone gridpoint fix velocity
zone face apply velocity-y -1e-5 ...
                range union position-y 1 position-y 3 position-y 5
zone initialize stress xx -1 yy -1 zz -1
;
[global z15 = zone.near(0.5, 4.5)]
[global z13 = zone.near(0.5, 2.5)]
[global z11 = zone.near(0.5, 0.5)]
fish define k0_d
    local s15 = zone.stress(z15)
    local s13 = zone.stress(z13)
    local s11 = zone.stress(z11)
    global k0_l = 0.5*(s15->xx+s15->zz)/s15->yy
    global k0_m = 0.5*(s13->xx+s13->zz)/s13->yy
    k0_d = 0.5*(s11->xx+s11->zz)/s11->yy
end
zone history displacement-y position 0 1
zone history stress-yy position 0.5 4.5
zone history stress-yy position 0.5 2.5
zone history stress-yy position 0.5 0.5
fish history [k0_d]
fish history [k0_m]
fish history [k0_l]
history interval 10
;
model step 1200
model save [string.build('oed%1', ICase)]