Bilinear Mohr-Coulomb Joint Model In 3DEC

The Bilinear Mohr-Coulomb Joint Model has two different shear strength envelopes. The failure envelope changes when a critical level of normal stress is exceeded. By default, the normal stress threshold is automatically calculated at the intersection of the two failure envelopes, but the user may override this default and specify any value. Both the peak and residual shear strengths can have bilinear envelopes and there may be different normal stress thresholds for the peak and the residual.

It is also possible to specify two different values of dilation, such that dilation angle changes when the residual normal stress threshold is exceeded. If a dilation angle for the high normal stress (\(\psi_2\)) is not given, its value defaults to the dilation of the low stress region (\(\psi_1\)).

Figure 1 shows an example. The low stress failure envelope has a friction angle, \(\phi_1\) = 30 degrees, and cohesion, \(c_1\) = 1 MPa. The high stress envelope has \(\phi_2\) = 20 degrees, and cohesion, \(c_2\) = 2 MPa. The normal stress threshold (cross-over) is calculated by:

\[\sigma_n^c = {{c_1 - c_2} \over {\tan\phi_2 - \tan\phi_1}}\]

Figure 1: Example bilinear failure envelope.

Subcontact failure state are the same as for the i Mohr-Coulomb Joint Model.

Summary of Bilinear Mohr-Coulomb Parameters

The model parameters associated with the bilinear mohr-coulomb model are summarized in Table 1. The model is accessed in 3DEC with the block contact jmodel assign bilinear-mohr command.

Table 1: Parameters associated with the Mohr-Coulomb joint model

Parameter	Description	Keyword
\(k_n\)	joint normal stiffness (STRESS/LENGTH)	stiffness-normal
\(k_s\)	joint shear stiffness (STRESS/LENGTH)	stiffness-shear
\(\phi\)	friction angle below sigma_n^c (DEGREES)	friction
\(\phi_2\)	friction angle above sigma_n^c (DEGREES)	friction-2
\(\phi_{res}\)	residual friction angle below sigma_n^c (DEGREES). Defaults to phi.	friction-residual
\(\phi_2^{res}\)	residual friction angle above sigma_n^c (DEGREES). Defaults to phi_2.	f2-residual
\(c\)	cohesion below sigma_n^c (STRESS)	cohesion
\(c_2\)	cohesion above sigma_n^c (STRESS)	cohesion-2
\(c_{res}\)	residual cohesion below sigma_n^c (STRESS). Defaults to 0.	cohesion-residual
\(c_2^{res}\)	residual cohesion above sigma_n^c (STRESS). Defaults to 0.	c2-residual
\(\psi\)	dilation angle below sigma_n^c (DEGREES)	dilation
\(\psi_2\)	dilation angle above sigma_n^c (DEGREES)	dilation-2
\(u_{cs}\)	shear displacement at which dilation stops (LENGTH). Default is infinity	dilation-zero
\(T_f\)	tensile strength (STRESS)	tension
\(T_f^{res}\)	residual tensile strength (STRESS). Default is 0.	tension-residual
\(\sigma_n^c\)	normal stress threshold (STRESS)	nstress
\(\sigma_n^c\)	normal stress threshold for residual envelope (STRESS)	nstress-residual

Examples

To view these examples in 3DEC, use the menu command Help -> Examples…. The main data files used are shown at the end of this example. All data files are found in the project.

A simple model is created from a 1×1×1 m block cut in half horizontally (Figure 2). The bottom block is held fixed. A normal stress is applied to the top of the top block. The top block is then moved horizontally to produce slip.

Figure 2: 3DEC Block configuration in the simple shear test.

Peak strength test

A single point in the middle of the intersecting faces is assigned the Bilinear Mohr-Coulomb joint material with the following shear strength parameters.

friction	\(\phi\)	30 degrees
friction-2	\(\phi_2\)	20 degrees
cohesion	\(c\)	1 MPa
cohesion-2	\(c_2\)	2 MPa

The default normal stress threshold is used (automatically calculated as 4.7 MPa). The normal stress is applied, and the model is sheared to failure. This was repeated multiple times for different normal stresses. The peak shear stress was measured for each model. The results are shown in Figure 3. The model behaves as expected.

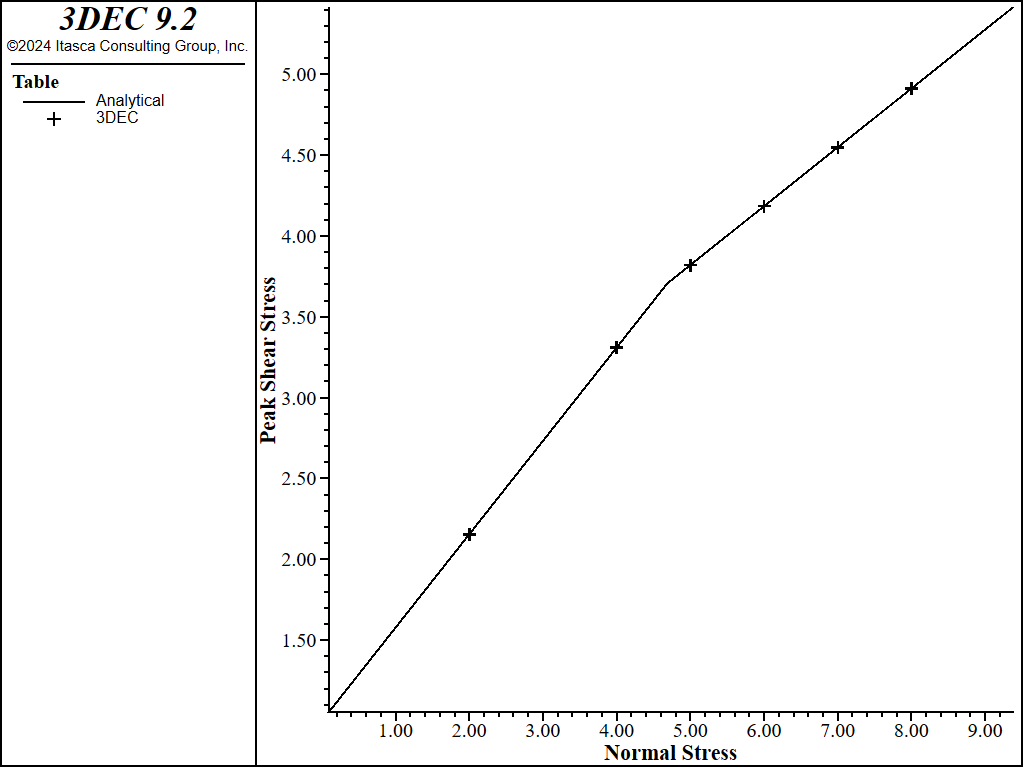
Figure 3: Peak shear strengths with different normal stresses.

Normal stress threshold tests

The same test is run, but the normal stress threshold is specified (instead of using the default). Two tests are run, one with a normal stress threshold below the default (3 MPa), and one with a normal stress threshold above the default (6 MPa). Results are shown in Figure 4 and Figure 5. The model behaves as expected.

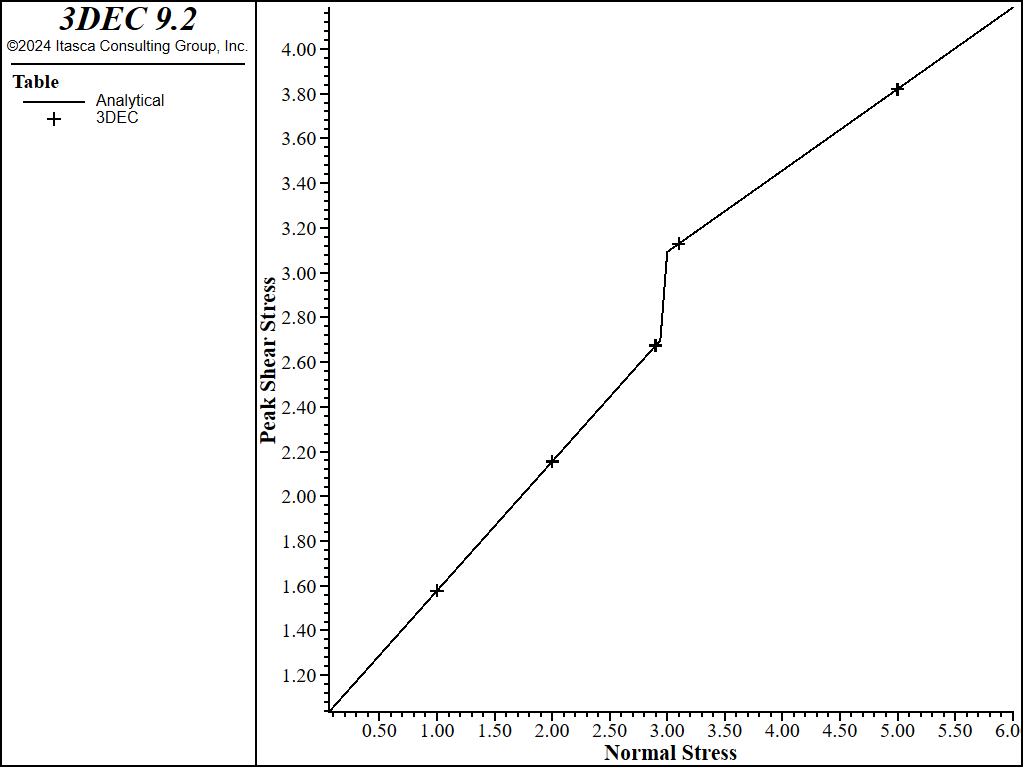
Figure 4: Peak shear strengths with different normal stresses with a stress threshold of 3 MPa.

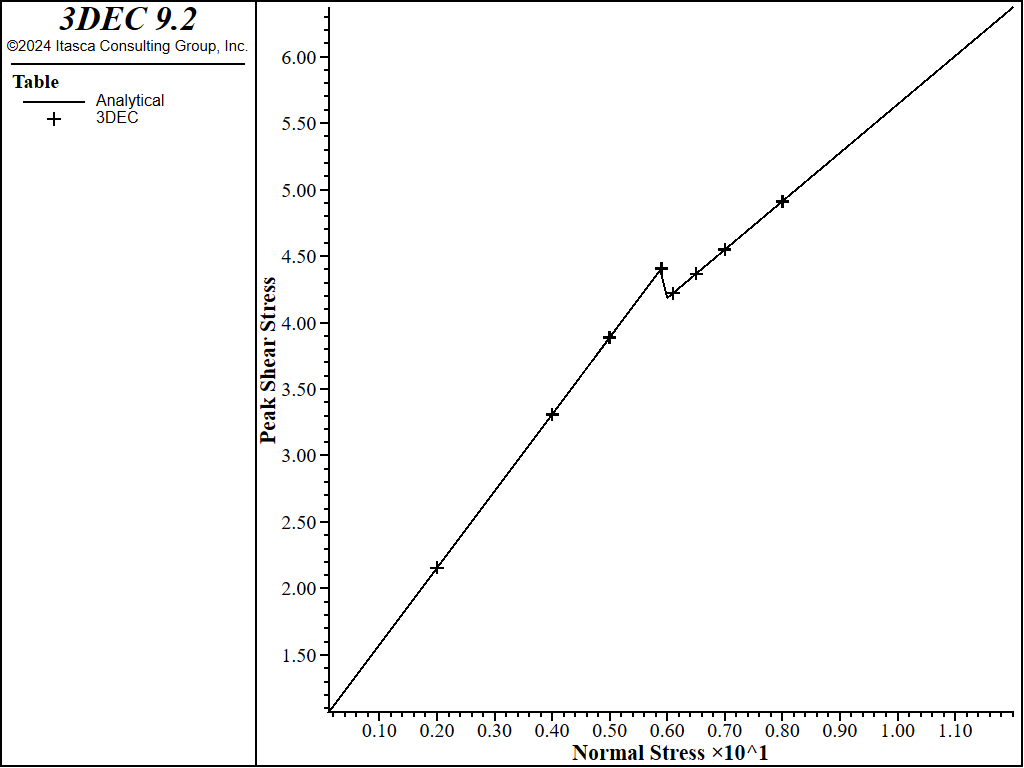
Figure 5: Peak shear strengths with different normal stresses with a stress threshold of 6 MPa.

Residual strength test

The same model is run using the following values for residual strengths:

friction-residual	\(\phi_{res}\)	30 degrees
f2-residual	\(\phi_2^{res}\)	20 degrees
cohesion-residual	\(c_{res}\)	0.5 MPa
c2-residual	\(c_2^{res}\)	1 MPa

The residual normal stress threshold was automatically calculated by 3DEC to be 2.3 MPa.

In this test a constant downward velocity is applied to the top boundary, causing the normal stress to gradually increase during shearing. The results are shown in Figure 6. The model behaves as expected.

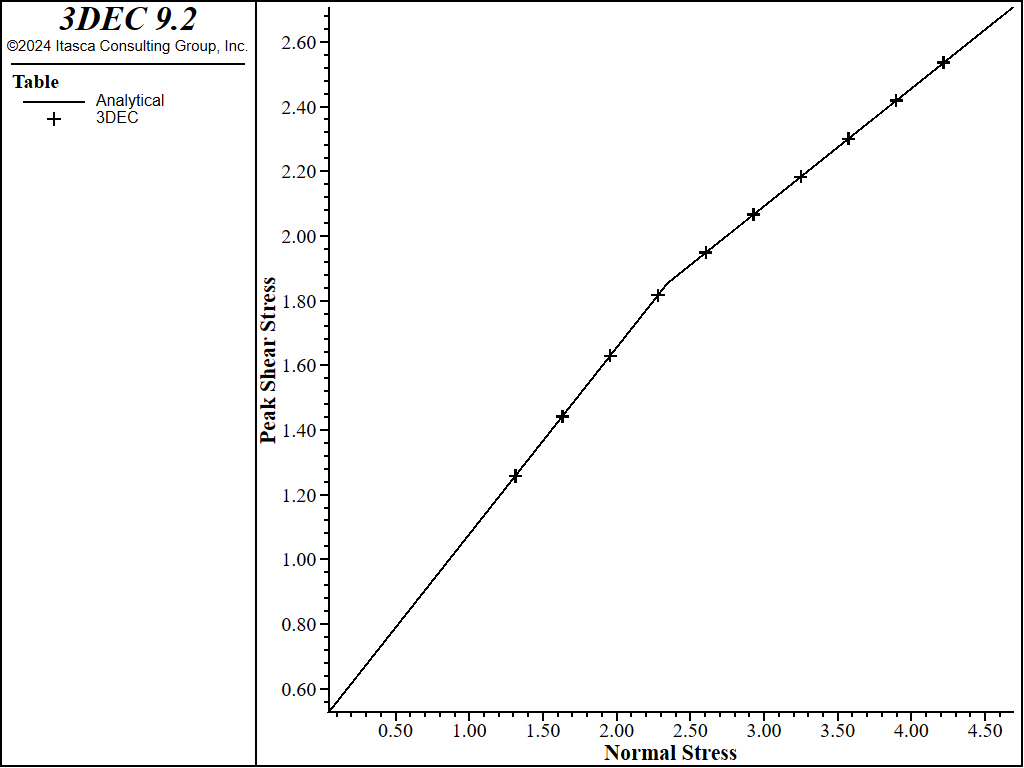
Figure 6: Shear strength of failed contact as normal stress increases.

Dilation test

The model is rerun with all subcontacts assigned the bilinear-mohr model. This is necessary so that the top block moves upwards uniformly when shear-induced dilation occurs. Dilation values are as follows.

dilation	\(\psi\)	10 degrees
dilation-2	\(\psi_2\)	5 degrees

The default residual normal stress threshold is used (2.3 MPa).

The top block is sheared as before. Normal stress is gradually increased by increasing levels of normal stress to the top boundary and cycling for 10,000 cycles at each level (i.e., normal stress is increased and then held constant for 10,000 steps while shearing). The dilation is calculated by observing the change in joint normal displacement and shear displacement over the last 1,000 steps of each normal stress cycle. The calculated dilation angles are shown in Figure 7.

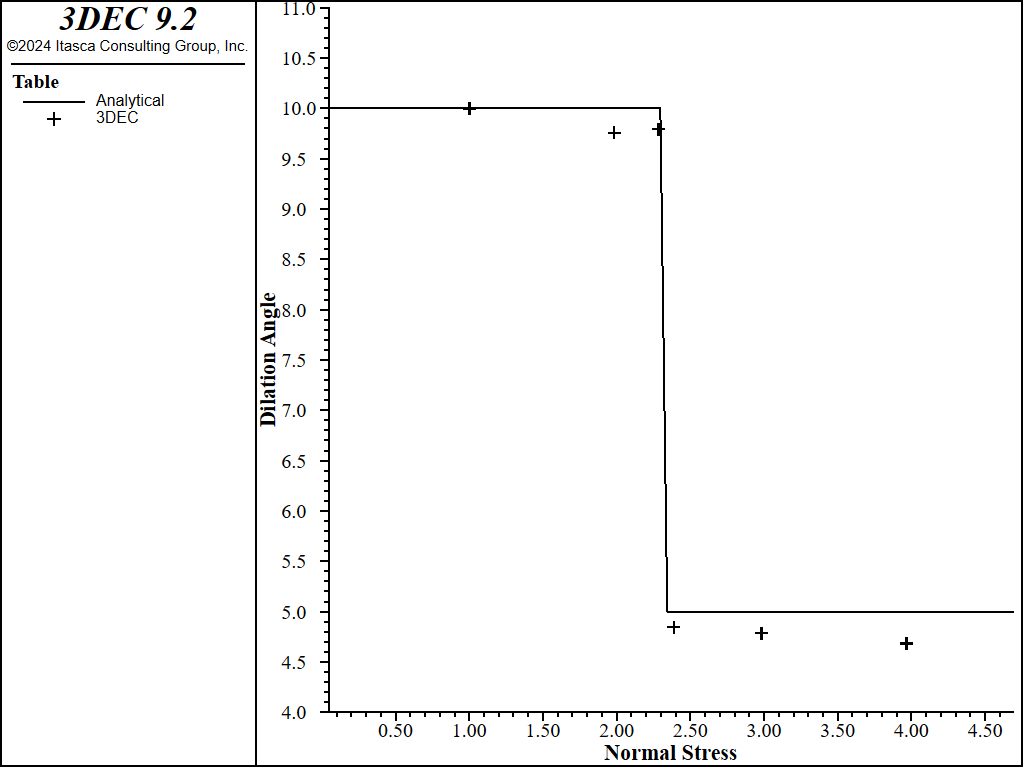
Figure 7: Dilation angles calculated at different values of normal stress.

Data Files

bmohr_test.dat

;
model new
model large-strain off
;
;
block create brick -1 1
block cut joint-set
;
; create central subcontact
block zone generate fix 0 0 0
block zone generate edgelength 2 fix 0 0 0

; use MPa
block zone cmodel assign elastic
block zone property density 2e-3 bulk 50e3 shear 30e3 
;
block contact jmodel assign bilinear-mohr
block contact property stiffness-normal 1e5 stiffness-shear 1e5 tension 1e6
;
; just assign strength to central subcontact
block contact property friction 30 friction-2 20 cohesion 1 cohesion-2 2 ...
                       range position-x -0.1 0.1 position-y -0.1 0.1
;
block fix range position-z -1 0
;
block hide range position-z -1 0
block gridpoint apply velocity-x 1e-4 range position-x -1 1
block hide off
;
block contact history stress-normal position 0 0 0
block contact history stress-shear position 0 0 0
block contact history displacement-shear position 0 0 0
;

; listension forigin the peak shear stress
program call 'analytical_peak.fis'
[setup]
;
fish callback add monitor 1.0
;
model save 'initial'

==============================================
;
[global filename = 'bmohr-peak.txt']
[openfile(filename)]

model save 'initial-peak'
;
; ===== Normal stress  2 MPa =======
;
block insitu stress 0 0 -2 0 0 0
block face apply stress-zz -2 range position-z 1
;
model cycle 15000
;
[dump(filename)]
;
; ===== Normal stress  4 MPa =======
;
model restore 'initial-peak'
;
;
block insitu stress 0 0 -4 0 0 0
block face apply stress-zz -4 range position-z 1
;
model cycle 25000
;
[dump(filename)]
;
; ===== Normal stress  5 MPa =======
;
model restore 'initial-peak'
;
;
block insitu stress 0 0 -5 0 0 0
block face apply stress-zz -5 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
; ===== Normal stress  6 MPa =======
;
model restore 'initial-peak'
;
;
block insitu stress 0 0 -6 0 0 0
block face apply stress-zz -6 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
; ===== Normal stress  7 MPa =======
;
model restore 'initial-peak'
;
;
block insitu stress 0 0 -7 0 0 0
block face apply stress-zz -7 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
; ===== Normal stress  8 MPa =======;
;
model restore 'initial-peak'
;
;
block insitu stress 0 0 -8 0 0 0
block face apply stress-zz -8 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
=======================================

[make_tables(filename)]
;

bmohr_nstress3.dat

model restore 'initial'
;
block contact property nstress 3 range position-x -0.1 0.1 position-y -0.1 0.1

[filename = 'bmohr-nstress3.txt']
;
[openfile(filename)]
;
model save 'initial-nstress3'
;
; ===== Normal stress = 1 MPa =====
;
block insitu stress 0 0 -1 0 0 0
block face apply stress-zz -1 range position-z 1
;
model cycle 15000
;
[dump(filename)]
;
; ===== Normal stress = 2 MPa =====
;
model restore 'initial-nstress3'
;
;
block insitu stress 0 0 -2 0 0 0
block face apply stress-zz -2 range position-z 1
;
model cycle 20000
;
[dump(filename)]
;
; ===== Normal stress = 2.9 MPa =====
;
model restore 'initial-nstress3'
;
block insitu stress 0 0 -2.9 0 0 0
block face apply stress-zz -2.9 range position-z 1
;
model cycle 25000
;
[dump(filename)]
;
; ===== Normal stress = 3.1 MPa =====
;
model restore 'initial-nstress3'
;
block insitu stress 0 0 -3.1 0 0 0
block face apply stress-zz -3.1 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
; ===== Normal stress = 4 MPa =====
;
model restore 'initial-nstress3'
;
block insitu stress 0 0 -4 0 0 0
block face apply stress-zz -4 range position-z 1
;
model cycle 30000
;
[dump('bmohr-nstress6.txt')]
;
; ===== Normal stress = 5 MPa =====
;
model restore 'initial-nstress3'
;
block insitu stress 0 0 -5 0 0 0
block face apply stress-zz -5 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
=======================================

[make_tables(filename)]

;
;

bmohr_nstress6.dat

model restore 'initial'
;
block contact property nstress 6 range position-x -0.1 0.1 position-y -0.1 0.1

[filename = 'bmohr-nstress6.txt']
;
[openfile(filename)]
;
model save 'initial-nstress6'
;
; ===== Normal stress = 2 MPa =====
;
block insitu stress 0 0 -2 0 0 0
block face apply stress-zz -2 range position-z 1
;
model cycle 15000
;
[dump(filename)]
;
; ===== Normal stress = 4 MPa =====
;
model restore 'initial-nstress6'
;
;
block insitu stress 0 0 -4 0 0 0
block face apply stress-zz -4 range position-z 1
;
model cycle 20000
;
[dump(filename)]
;
; ===== Normal stress = 5 MPa =====
;
model restore 'initial-nstress6'
;
block insitu stress 0 0 -5 0 0 0
block face apply stress-zz -5 range position-z 1
;
model cycle 25000
;
[dump(filename)]
;
; ===== Normal stress = 5.9 MPa =====
;
model restore 'initial-nstress6'
;
block insitu stress 0 0 -5.9 0 0 0
block face apply stress-zz -5.9 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
; ===== Normal stress = 6.1 MPa =====
;
model restore 'initial-nstress6'
;
block insitu stress 0 0 -6.1 0 0 0
block face apply stress-zz -6.1 range position-z 1
;
model cycle 30000
;
[dump('bmohr-nstress6.txt')]
;
; ===== Normal stress = 6.5 MPa =====
;
model restore 'initial-nstress6'
;
block insitu stress 0 0 -6.5 0 0 0
block face apply stress-zz -6.5 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
; ===== Normal stress = 7 MPa =====
;
model restore 'initial-nstress6'
;
block insitu stress 0 0 -7.0 0 0 0
block face apply stress-zz -7.0 range position-z 1
;
model cycle 30000
;
[dump(filename)]
;
; ===== Normal stress = 8 MPa =====
;
model restore 'initial-nstress6'
;
;
block insitu stress 0 0 -8.0 0 0 0
block face apply stress-zz -8.0 range position-z 1
;
model cycle 30000
;
[dump(filename)]

=======================================

[make_tables(filename)]
;
;

dilation.dat

model new
model large-strain off
;
block create brick -1 1 -1 1 -1 1
block cut joint-set
;
; create central subcontact
block zone generate fix 0 0 0
block zone generate edgelength 2 fix 0 0 0

; properties in MPa
block zone cmodel assign elastic
block zone property density 2e-3 bulk 50e3 shear 30e3 
;
;
block contact jmodel assign bilinear-mohr
block contact property stiffness-normal 1e5 stiffness-shear 1e5 tension 1e6
;
; here we assign properties to the entire fault
block contact property friction 30 friction-2 20 cohesion 1 cohesion-2 2
block contact property friction-residual 30 f2-residual 20 ...
                       cohesion-residual 0.5 c2-residual 1
block contact property dilation 10 dilation-2 5
block fix range position-z -1 0
;
block hide range position-z -1 0
block gridpoint apply velocity-x 1e-4 range position-x -10 10
block hide off
;
block contact history stress-normal position 0 0 0
block contact history stress-shear position 0 0 0
block contact history displacement-shear position 0 0 0
block contact history displacement-normal position 0 0 0
;
;
block insitu stress 0 0 -1 0 0 0
block face apply stress-zz -1 range position-z 1
;
model cycle 5000
;
model save 'failed'
;
=======================================
;
;
model restore 'failed'
;
history purge

program call 'analytical_dilation.fis'
[setup]
;
; store current displacements on middle point
[store_dis]
;
; ==== Normal stress = 1 MPa ===============
;
model cycle 1000
;
; calculate dilation and add to table
[calc_dilation]
;
; ===== Normal stress = 2 MPa ==============

; adds to previous!  total = 2 MPa
block face apply stress-zz -1 range position-z 1
;
model cycle 4000
[store_dis]
model cycle 1000
[calc_dilation]
;
; === Normal stress = 2.3 =====
block face apply stress-zz -0.3 range position-z 1
;
model cycle 4000
[store_dis]
model cycle 1000
[calc_dilation]
;
; ==== Normal stress = 2.4 =====
block face apply stress-zz -0.1 range position-z 1
;
model cycle 4000
[store_dis]
model cycle 1000
[calc_dilation]
;
; ==== Normal stress = 3 =====
block face apply stress-zz -0.6 range position-z 1
;
model cycle 4000
[store_dis]
model cycle 1000
[calc_dilation]
;
; ==== Normal stress = 4 =====
block face apply stress-zz -1 range position-z 1
;
model cycle 4000
[store_dis]
model cycle 1000
[calc_dilation]

[calc_dilation_analytical]
;

Properties

bilinear-mohr

cohesion f

Joint cohesion for normal stress less than nstress.

cohesion-2 f

Joint cohesion for normal stress greater than nstress.

cohesion-residual f

Residual joint cohesion for normal stress less than nstress-residual.

c2-residual f

Residual joint cohesion for normal stress greater than nstress-residual.

dilation f

Joint dilation angle in degrees for normal stress less than nstress-residual.

dilation-2 f

Joint dilation angle in degrees for normal stress greater than nstress-residual.

dilation-zero f

Shear displacement at which joint will cease to dilate.

friction f

Peak friction angle in degrees for normal stress less than nstress.

friction-2 f

Peak friction angle in degrees for normal stress greater than nstress.

friction-residual f

Residual joint friction angle in degrees for normal stress less nstress-residual.

f2-residual f

Residual joint friction angle in degrees for normal stress greater than nstress-residual.

nstress f

Normal stress threshold at which peak friction and cohesion changes. If not provided, this is calculated automatically from the cross-over of the two peak failure envelopes.

nstress-residual f

Normal stress threshold at which residual friction and cohesion changes. If not provided, this is calculated automatically from the cross-over of the two residual failure envelopes.

stiffness-normal f

Joint normal stiffness (stress / distance).

stiffness-shear f

Joint shear stiffness (stress / distance).

tension f

Tensile strength.

tension-residual f

Residual joint tensile tensile.