FLAC3D Theory and Background • Constitutive Models

Hoek-Brown Model

This model is derived directly from the Mohr-Coulomb model, and, like the Mohr-Coulomb model, can be used to perform factor of safety calculations using the model factor-of-safety command.

The Hoek-Brown-PAC model provides a representation for yielding that accounts for the changing failure condition. This model works well at higher confining stress states, but can produce excessive dilation at low confinement or under tensile-stress conditions. The alternative version, described in this section, is modified to include a tensile yield criterion, and also allow the user to specify a dilation angle as an input parameter and manually control the level of dilation that develops.

The formulation and an example exercise are given below.

Formulations

The Hoek-Brown criterion is used for plastic yielding when the minor principal stress, \(\sigma_3\), is compressive. The criterion is based on a nonlinear relation between major and minor principal stresses, \(\sigma_1\) and \(\sigma_3\), as shown previously in the Hoek-Brown-PAC model, and repeated here:

(1)\[ \sigma_1 = \sigma_3+ \sigma_{ci} {\left( m_b{\sigma_3\over\sigma_{ci}} +s \right)}^a\]

where \(\sigma_{ci}\) is the unconfined compressive strength of the intact rock, and \(m_b\), \(s\), and \(a\) are material constants that can be related to the geological strength index (GSI) and rock damage (disturbance) factor \(D\), and parameter \(m_i\) (Hoek et al., 2002):

(2)\[ m_b = m_i \exp \left( \frac{GSI-100}{28-14D} \right)\]

(3)\[ s = \exp \left( \frac{GSI-100}{9-3D} \right)\]

(4)\[ a = \frac{1}{2} + \frac{1}{6} \left[ \exp{\left(\frac{-GSI}{15}\right)} - \exp{\left(\frac{-20}{3}\right)}\right]\]

If GSI = 100, the above equations give \(m_i = m_b\), \(s=1\) and \(a=0.5\).

The Hoek-Brown envelope is extended for \(\sigma_3\) tensile by a combination of the Mohr-Coulomb envelope (tangent to Hoek-Brown at \(\sigma_3 = 0\)) and a tensile cutoff at \(\sigma_3 = -s \sigma_{ci} / m_b\).

The numerical implementation of the Hoek-Brown model uses a linear approximation (see Figure 1), whereby the nonlinear failure surface is continuously approximated by the Mohr-Coulomb tangent at the current stress level, \(\sigma_3\). The current tangent Mohr-Coulomb criterion is

(5)\[ \sigma_1\ =\ \sigma_3 N_{\phi_c}\ +\ 2 c_c \sqrt{N_{\phi_c}}\]

where

(6)\[ N_{\phi_c}\ =\ {1 + \sin \phi_c \over {1 - \sin \phi_c}}\ =\ \tan^2({\phi_c \over {2}} + 45^{\circ})\]

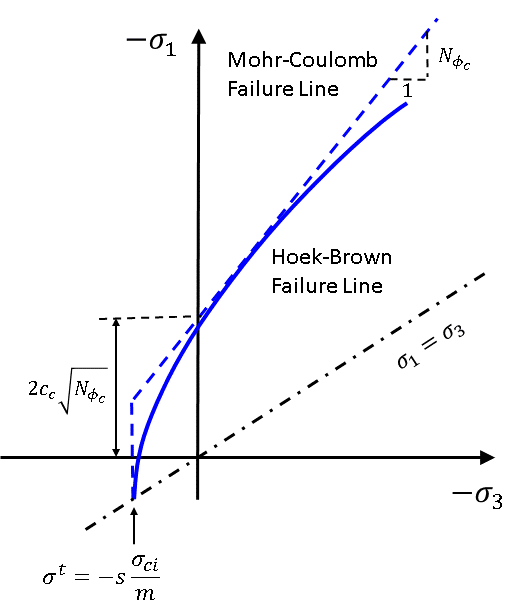
Figure 1: Hoek-Brown failure criterion and its Mohr-Coulomb approximation.

The current (apparent) value of cohesion, \(c_c\), and friction, \(\phi_c\), are calculated using

(7)\[ \phi_c\ =\ \sin^{-1} \left( {{N_{\phi_c} -1} \over {N_{\phi_c} +1}} \right)\]

(8)\[ c_c\ =\ {\sigma^{ucs}_c \over {2\sqrt{N_{\phi_c}}}}\]

where

(9)\[ N_{\phi_c}\ =\ 1 + am_b {\Bigl(m_b {\sigma_3 \over \sigma_{ci}} + s \Bigr)}^{a-1}\]

(10)\[ \sigma^{ucs}_c =\ \sigma_3 (1 - N_{\phi_c}) + \sigma_{ci} {\Bigl(m_b {\sigma_3 \over \sigma_{ci}} + s \Bigr)}^a\]

The Mohr-Coulomb envelope extension in the region of tensile \(\sigma_3\) is accounted for in the logic by considering the following cap in Equations (9) and (10) (recall that compressive stress is positive):

(11)\[ \sigma_3\ =\ \max(\sigma_3,0)\]

..The tensile yield logic is the same as the one used for the strain-softening/hardening Mohr-Coulomb model.

The plastic strain increment for shear yielding is defined using the current Mohr-Coulomb flow rule:

(12)\[ \Delta e_{ij}^{p} = \Delta e^p {\partial g \over \partial \sigma_{ij}} - {1 \over 3} \Delta e_{vol}^p \delta_{ij} \qquad i=1,3\]

where \(\Delta e^p\) is the plastic flow increment intensity, \(g\) is the plastic potential function, and

(13)\[ \Delta e_{vol}^p = \Delta e^p \Bigl({\partial g \over \partial \sigma_{11}} + {\partial g \over \partial \sigma_{22}} + {\partial g \over \partial \sigma_{33}}\Bigr)\]

The plastic potential function is

(14)\[ g = \sigma_1 - \sigma_3 N_{\psi_c}\]

where \(\psi_c\) is the current value of dilation and

(15)\[ N_{\psi_c} = {1+\sin{\psi_c} \over 1-\sin{\psi_c}}\]

The direction of plastic flow (\({\partial g \over \partial \sigma_{ij}}\) in Equation (12)) is expressed using the plastic potential function. The plastic flow increment intensity, \(\Delta e^p\), is derived from the current tangent Mohr-Coulomb yield criterion, Equation (12). There are three choices of flow rule for the model:

1. Input a dilation angle (\(\psi_c\) is a constant value) specified by property keyword constant-dilation and flag-dilation = 0.

2. Specify associated plastic flow (\(\psi_c\) is set equal to \(\phi_c\)) by setting flag-dilation = -1.

3. Set dilation as a fraction of the friction angle (\(\psi_c\) is set to a constant time \(\phi_c\)); flag-dilation is a positive fraction.

Strain hardening/softening behavior can be prescribed for the Hoek-Brown properties, \(m_b\), \(s\), \(a\), and \(\sigma_{ci}\). The input is via tables, in terms of an evolution parameter. There are two choices for evolution parameter: plastic shear strain (property keyword flag-evolution is set to 1, only accumulated when shear yielding occurs), or plastic strain in the direction of the least compressive principal stress, \(\sigma_3\) (property keyword flag-evolution is set to 0). The evolution parameter can be monitored via the property strain-plastic.

A simple regularization technique can be selected to address the issue of grid dependency on softening behavior. To activate this technique, the grid zone size used to calibrate model properties with experimental data is assigned to the property length-calibration, \(L_c\). This property is the calibration length. The input softening rate is then adjusted automatically by a factor of \(L_c/\sqrt[3]{V_z}\) (\(V_z\) is the zone volume) to account for a different zone size used in the full FLAC3D or 3DEC model. Note that this technique is experimental and should be used with caution.

References

Hoek, E., and E. T. Brown. “Practical Estimates of Rock Mass Strength,” Int. J. Rock Mech. Min. Sci., 34 (8), 1165-1186 (1998).

Hoek, E., and E. T. Brown. Underground Excavations in Rock. London: IMM (1980).

Hoek, E., C. Carranza-Torres and B. Corkum. “Hoek-Brown Failure Criterion — 2002 Edition,” in Proceedings of NARMS-TAC 2002, 5th North American Rock Mechanics Symposium and 17th Tunnelling Association of Canada Conference — Toronto, Canada — July 7 to 10, 2002. Vol.~1., pp. 267-271. R. Hammah et al., eds. Toronto: University of Toronto Press (2002).

Examples

Open Pit Mine with Faults

Simple Slope in Hoek-Brown Material

Triaxial Compression Test with Hoek-Brown Model

hoek-brown Model Properties

Use the following keywords with the zone property command to set these properties of the Hoek-Brown model.

hoek-brown

bulk f

bulk modulus, \(K\)

constant-a f

Hoek-Brown parameter, \(a\)

constant-dilation f

dilation angle, \(\psi_c\), required only when flag-dilation = 0. The default is 0.0.

constant-mb f

Hoek-Brown parameter, \(m_b\)

constant-mi f

Hoek-Brown parameter, \(m_i\)

constant-s f

Hoek-Brown parameter, \(s\)

constant-sci f

Hoek-Brown parameter, \(\sigma_{ci}\)

current-a f

current value of \(a_c\)

current-mb f

current value of \(m_{b,c}\)

current-s f

current value of \(s_c\)

current-sci f

current value of \(\sigma_{ci,c}\)

disturbance f

Hoek-Brown parameter, \(D\)

geological-strength-index f

Hoek-Brown parameter, GSI

poisson f

Poisson’s ratio, \(\nu\)

shear f

shear modulus, \(G\)

tension f

current value of tensile strength, \(\sigma^t\). The default is 0.0.

young f

Young’s modulus, \(E\)

flag-brittle b (a)

If true, the tension limit is set to 0 in the event of tensile failure. The default is false.

length-calibration f (a)

calibration length to calibrate model properties to account for zone size, default value is 0.0, which means that it does not perform length calibration to account for zone size.

flag-dilation f (a)

= 0 (default flag) to input a constant dilation angle specified by constant-dilation

= -1 to specify associated plastic flow, \(\psi_c\) = \(\phi_c\)

= k where k is a fraction of friction angle, \(\phi_c\), so that \(\psi_c\) = \(k \times \psi_c\)

flag-evolution i (a)

= 0 (default flag) for evolution parameter set to plastic strain in direction of least compressive principal stress

= 1 for evolution parameter set to plastic shear strain, only accumulated when shear yielding occurs

flag-fos i (a)

= 0 (default flag) for model factor-of-safety solution controlled by shear strength

= 1 for model factor-of-safety solution controlled by unconfined compressive strength

strain-plastic f (a)

plastic strain in direction of least compressive principal stress (if flag-evolution = 0), or plastic shear strain (if flag-evolution = 1)

table-a s (a)

name of the table relating \(a\) to the evolution parameter.

table-mb s (a)

name of the table relating \(m_b\) to the evolution parameter.

table-multiplier s (a)

name of the table relating a multiplier to \(\sigma_3\).

table-s s (a)

name of the table relating \(s\) to the evolution parameter.

table-sci s (a)

name of the table relating \(\sigma_{ci}\) to the evolution parameter.

table-tension s (a)

name of the table relating \(\sigma^t\) to plastic tensile strain.

cohesion f (r)

current value of cohesion, \(c_c\)

dilation f (r)

current value of dilation angle, \(\psi_c\), in any cases, this value never greater than the current friction angle.

friction f (r)

current value of friction angle, \(\phi_c\)

plastic-strain t (r)

accumulated plastic shear strain tensor. If model plastic-strain is set to true (or on or yes), the plastic strain tensor is accumulated. If model plastic-strain is set to false (or off or no), the plastic strain tensor is stopped for accumulated.

Key

(a) Advanced property.

This property has a default value; simpler applications of the model do not need to provide a value for it.

(r) Read-only property.

This property cannot be set by the user. Instead, it can be listed, plotted, or accessed through FISH.

Notes

• Only one of the two options is required to define the elasticity: bulk modulus \(K\) and shear modulus \(G\), or, Young’s modulus \(E\) and Poisson’s ratio \(\nu\). When choosing the latter, Young’s modulus \(E\) must be assigned in advance of Poisson’s ratio \(\nu\).

• The tension cut-off is \({\sigma}^t = min({\sigma}^t, c/\tan \phi)\).

• There are two sets of parameters for (\(a\), \(m_b\), \(s\), \(\sigma_{sci}\)): one is called constant set, which are the values assigned at the first time and remain constant thereafter; the other is called current set, which are automatically initialized as the same values of the constant set, but can be updated thereafter using tables or FISH functions if parameter evolution/update is involved, otherwise, the current set can be considered only for output.

• The tension table and flag-brittle should not be active at the same time.

• The inputs can be (GSI, \(D\), \(m_i\)) or (\(a\), \(s\), \(m_b\)). Once \(a\), \(s\), and \(m_b\) are all zero, GSI and \(m_i\) should be input positive values, the first group of parameters will be used, and the second group parameters will be calculated internally at initialization. Otherwise, the second group of parameters should be assigned.