FLAC3D Theory and Background • Constitutive Models

Soft-Soil Model*

Note

*Not available in 3DEC.

Soft soils generally refer to normally consolidated or slightly over-consolidated clays, silty-clays, clayey silts, and peats. Significant compression (e.g., \(E^{ref}_{oed} < 0.5 E^{ref}_{50}\)) is one of the main engineering characteristics of the soft soils. The soft-soil (SS) model has the following features: (a) pressure-dependent moduli; (b) unloading-reloading distinct from the virgin loading; (c) expansion of the volumetric yield ellipse-shaped cap; and (d) conventional Mohr-Coulomb shear failure and tension failure criteria.

In the SS model, the virgin compression assumes the relation

(1)\[\Delta \epsilon_v = - \frac{\lambda^* \Delta p}{p+c\cot{\phi}}\]

where \(\Delta \epsilon_v\) is the increment of the volumetric strain, \(\Delta p\) is the increment of the mean pressure, and material parameters \(c\) and \(\phi\) are the cohesion and friction angle of the soil, respectively. The material parameter \(\lambda^*\) is the modified compression index.

The unloading and reloading compression assumes

(2)\[\Delta \epsilon^e_v = - \frac{\kappa^* \Delta p}{p+c\cot{\phi}}\]

where \(\Delta \epsilon^e_v\) is the increment of the elastic volumetric strain, and the material parameter \(\kappa^*\) is the modified swelling index. Equation (2) implies that the elastic bulk modulus is pressure-dependent and with the form

(3)\[K = \frac{p+c\cot{\phi}}{\kappa^*}\]

It is noted that the material parameters \(\lambda^*\) and \(\kappa^*\) (using the superscript asterisk to denote “modified”) are based on the increment of volumetric strains (Figure 1); they are different from the material parameters \(\lambda\) and \(\kappa\) used in the modified Cam-Clay model which are based on the increment of void ratios.

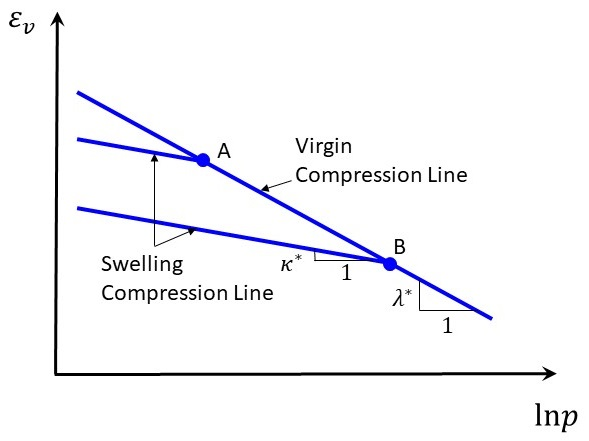
Figure 1: Relation between the volumetric strain \(\epsilon_v^p\) and the effective mean pressure \(p\).

The model assumes a constant Poisson’s ratio \(\nu\) , so the elastic shear modulus is

(4)\[G = \frac{3(1-2\nu)}{2(1+\nu)} K\]

The pre-consolidation pressure, or cap pressure, \(p_c\), is the largest pressure level experienced by the soil. During the virgin (primary) loading, \(p_c\) increases with the stress level and causes the plastic (irreversible) volumetric strains. By Equations (1) and (2) together with \(\Delta \epsilon_v = \Delta \epsilon^e_v + \Delta \epsilon^p_v\), it can be derived that

(5)\[\Delta p_c = -p_c \frac{\Delta \epsilon^p_v}{\lambda^* - \kappa^*}\]

The yield surface of the SS model is an ellipse in the \((p,\tilde{q})\) plane (Figure 1) expressed as

(6)\[f = p_{eq} - p_c\]

where the equivalent pressure is defined as

(7)\[p_{eq} = p + \frac{\tilde{q}^2}{M^{*2}(p+c\cot{\phi})}\]

and \(p=-(\sigma_1+\sigma_2+\sigma_3)/3\), \(\tilde{q}=-[\sigma_1+(\delta-1)\sigma_2-\delta\sigma_3]\), where \(\sigma_1\), \(\sigma_2\), and \(\sigma_3\) are effective principal stress with the order \(\sigma_1 \leq \sigma_2 \leq \sigma_3\), \(\delta=(3+\sin{\phi})/(3-\sin{\phi})\), and \(M^*\) determines the ratio of the radius of the ellipse defined by the yield function as Equation (6). Here \(M^*\) is different from the value of \(6\sin{\phi}/(3-\sin{\phi})\) in the modified Cam-Clay model. Instead, \(M^*\) is not an input material parameter but internally determined by other material parameters by the relation (Brinkgreve, 1994)

(8)\[M^* = 3 \sqrt{\frac{(1-K_{nc})^2}{(1+2K_{nc})^2} + \frac{(1-K_{nc})(1-2\nu)(\lambda^*-\kappa^*)}{(1+2K_{nc})(1-2\nu)\lambda^* - (1-K_{nc})(1+\nu)\kappa^*}}\]

where \(K_{nc}\) is the coefficient of lateral earth pressure in a normally consolidated condition, and the user can input a value or its default value is \(K_{nc} = 1 - \sin{\phi}\) if not assigned.

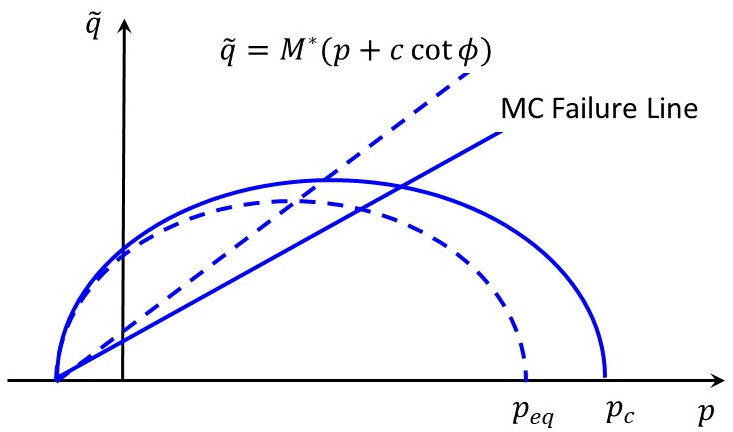
Figure 2: Yield and failure surfaces of the Soft-Soil model in the \((p, \tilde{q})\) plane.

The SS model uses the associated flow rule for the volumetric evolution, so the potential function \(g\) for volumetric plasticity is the same as the yield function in Equation (6)

(9)\[g = f = p_{eq} - p_c\]

The conventional Mohr-Coulomb shear failure and tension failure criteria are also adopted in the SS model. The elastic region is defined by the volumetric yield ellipse, the Mohr-Coulomb shear failure line, and the tension failure line in the \((p,\tilde{q})\) plane.

If the creep effect of the secondary compression would be taken into account, the Soft-Soil-Creep model is recommended.

References

Brinkgreve, R.B.J. Geomaterial models and numerical analysis of softening. Ph.D. Thesis. Univ., Delft, Netherlands (1994).

Examples

One-Dimensional Consolidation Considering Secondary Compression
Undrained Triaxial Test with Soft-Soil Model

soft-soil Model Properties

Use the following keywords with the zone property command to set these properties of the Soft-Soil model.

soft-soil

friction f

friction angle, \(\phi\), The default value is 30 [in degrees]. The recommended input value is the critical-state friction angle rather than a higher value at small strains. Input of a zero value is not allowed.

kappa-modified f

modified swelling index, or slope of elastic swelling line, \(\kappa^*=\kappa/(1+e)\), where \(\kappa\) is the swelling index in the Cam-Clay model, and \(e\) can be approximately the initial or average void ratio during a swelling path; or \(\kappa^* \approx [(1+2K_0)(1-\nu)/(1+\nu)] C_s/[(\ln{10})(1+e)]\), where \(C_s\) is the 1-D swelling index, \(\nu\) is the Poisson’s ratio and \(K_0\) is the at-rest earth pressure coefficient. Typical value of \(C_s\) is \(C_s \approx (1/5) \sim (1/10) C_c\). A good estimation is \(C_s \approx PI(\%)/370\).

lambda-modified f

modified compression index, or slope of elastic compression line, \(\lambda^*=\lambda/(1+e)\), where \(\lambda\) is the compression index in the Cam-Clay model, and \(e\) can be approximately the initial or average void ratio during a compression path; or \(\lambda^*=C_c/[(\ln{10})(1+e)]\), where \(C_c\) is the 1-D compression index. Typical value of \(C_c\) can be estimated (Terzaphi & Peck 1967) as \(C_c=0.009(LL-100)\) for normally consolidated clay where \(LL\) is the liquid limit. Based on the modified Cam-Clay model, it can estimated that \(C_c \approx PI(\%)/74\), where \(PI\) is the plastic index.

poisson f

Poisson’s ratio, \(\nu\), The default value is 0.15.

stress-1-effective f

initial minimum effective principal stress, \(\sigma^0_1\). Only for calculation of the initial moduli, will not be update once assigned.

stress-2-e f

initial median effective principal stress, \(\sigma^0_2\). Only for calculation of the initial moduli, will not be update once assigned.

stress-3-effective f

initial maximum effective principal stress, \(\sigma^0_3\). Only for calculation of the initial moduli, will not be update once assigned.

coefficient-normally-consolidation f (a)

normal consolidation coefficient, \(K_{nc}\). It is not allowed to be less than \(\nu / (1-\nu)\), a range 0.5 to 0.7 is common. The default is \(K_{nc} = 1 - \sin \phi\).

cohesion f (a)

effective cohesion, \(c\). The default value is 0. Remember that this model is mainly for normally consolidated or slightly over-consolidated soft soils, so \(c\) should be zero or a small value, and a large value may be not realistic.

dilation f (a)

dilation angle, \(\psi\). The default value is 0 [in degrees]. The zero dilation angle is the standard setting in the SS model.

flag-brittle b (a)

If true, the tension limit is set to 0 in the event of tensile failure. The default is false.

over-consolidation-ratio f (a)

over consolidation ratio, \(OCR\). The default is 1.0, which corresponds to the normally consolidated soils. The input \(OCR\) will be used to determine the initial cap pressure so that \(p_{c}^0=OCR \times p_{eq}^0\). \(OCR\) will be updated during calculation.

pressure-cutoff f (a)

cut-off pressure for cap pressure, \(p_{cut}\). The default value is 1.0 (of the stress unit used in the model). This is the lower-bound of the cap pressure. The actual minimum cap pressure used in the model is \(max(p_{cut}, c\cot{\phi})\).

ratio-radius f (a)

parameter \(M^*\), if not assigned a positive value, it will be calculated internally.

tension f (a)

tensile strength, \(\sigma^t\). The default value is 0, which is for most cases.

void-initial f (a)

initial void ratio, \(e_{ini}\). The default is 1.0.

bulk f (r)

current elastic bulk modulus, \(K\)

pressure-cap f (r)

current cap (apparent pre-consolidation) pressure, \(p_c\)

pressure-effective f (r)

current effective pressure, \(p\)

pressure-equivalent f (r)

current equivalent pressure, \(p_{eq}\)

shear f (r)

current elastic shear modulus, \(G\)

strain-volume-plastic f (r)

accumulated plastic volumetric strain, \(\epsilon_v^p\)

stress-deviatoric-equivalent f (r)

current equivalent deviatoric stress, \(\tilde{q}\)

void f (r)

current void ratio, \(e\)

Key

(a) Advanced property.

This property has a default value; simpler applications of the model do not need to provide a value for it.

(r) Read-only property.

This property cannot be set by the user. Instead, it can be listed, plotted, or accessed through FISH.