Genesis and Testing of a Soft-Bonded Material
Problem Statement
Note
The project file for this example may be viewed/run in PFC.[1] The data files used are shown at the end of this example.
The following example illustrates genesis and testing of a bonded-particle model using the Soft-Bond contact model. The system composed of balls is first generated in a periodic domain, then settled under low confining stress. This is achieved by distorting the periodic domain dimensions in order to achieve the prescribed stress state, using a servo-algorithm implemented as a FISH function. The soft-bond contact model is then installed at existing contacts, while the contact forces are reset. From this initial, stress-free system, the following tests are performed: a direct tension test, an unconfined compression test and a confined compression test. The methodologies used at each stage of the modeling process are discussed, and the response of the material is investigated.
Numerical Model
Specimen Genesis
The initial packing is generated by calling the file make_brick.dat, which uses the FISH functions defined in servo.fis. The specimen is generated in the entire model domain, with periodic boundary conditions in all directions, to avoid boundary effects. The function servo_domain implements the servo-control algorithm procedure, which aims at updating the domain extent in each direction in order to achieve and maintain a prescribed stress. The stress in the specimen is monitored using a measurement sphere. Note that this sphere is extended to encompass the entire domain, and the value of the stress that it computes is scaled to use the actual volume of the domain.
At this stage, the objective is to generate a dense, well connected packing. Since the contact model and properties will be overridden in a subsequent stage, a simple linear contact model is used. The friction coefficient is set to zero, and the deformability of the contacts is set to a value reasonably large with respect to the prescribed target stress, to optimize the computation time while preventing large overlaps. Note that increasing the target stress, or using frictional contacts would modify the geometry of the packing, and therefore its subsequent behavior.
The file make_brick.dat is partially parameterized for convenience. The file doall_A10.dat demonstrates how it can be executed, and the parameters chosen in this example:
; Generate packing
model random 10001
[resolution = 10] ; approx. number of balls accross specimen width
[davg = 2.5e-3] ; average ball diameter (m)
[dratio = 1.66] ; ball max/min diameter ratio [-]
[tag = 'A'+ string(resolution)]
program call 'make_brick.dat'
The average ball diameter is set to 2.5mm, with a maximum to minimum diameter ratio of 1.66, to prevent local arrangement of the balls into crystalline structures. The parameter resolution used in this example denotes the target number of balls across the lateral dimension of the specimen, which is set to have a 2:1 aspect ratio.
Contact Model and Properties
Once the initial packing has been created, the file bond_sb.dat is used to install the soft-bond contact model and prepare the specimen for further testing. The contact forces are reset to zero, as well as the translational and rotational velocities of the balls and their accumulated forces/moments and displacements, and the contact model is replaced with the soft-bond model. Please refer to the documentation of this contact model for a detailed description of its behavior and properties.
The file bond_sb.dat is partially parameterized for convenience. The file doall_A10.dat demonstrates how it can be executed, and the parameters chosen in this example follow:
; Install contact model
model restore [string.build('brick_%1-iso',tag)]
[igap = 0.0*davg ]
[emod = 50.0e9 ]
[kratio = 2.5 ]
[fric = 0.5 ]
[ten_mean = 20.0e6 ]
[ten_std = 0.0e6 ]
[coh_mean = 100.0e6 ]
[coh_std = 0.0e6 ]
[soft = 0.0 ]
[cut = 1.0 ]
[tag += '_G0_E50_KR25_S0_C1']
program call 'bond_sb.dat'
The contact effective modulus is set to 50GPa, with a normal-to-shear stiffness ratio of 2.5 and a friction coefficient of 0.5. The contact tensile strength is set to 20MPa and the cohesion to 100MPa. Note that although the file bond_sb.dat is set to allow for a normal distribution of the strength parameters to be set, this functionality is not used in this example and all contacts are assigned the same strength parameters. Finally, the softening coefficient is set to 0.0 and the softening tensile strength factor is set to unity. With these values, softening is prohibited, and the model behaves essentially similar to the linear parallel-bond contact model with respect to failure.
Direct Tension Test
Two methods to simulate a direct tension test are described and compared below. The first method identifies balls on the two opposite ends of the specimen in the vertical direction, and fixes their velocity. The second method distorts the domain outward in the vertical direction.
Method 1: Using Ball Fixity
The file tt.dat is used to perform the direct tension test by fixing the velocities of a top and a bottom layer of balls. It is partially parameterized for convenience, and the file doall_A10.dat demonstrates how it can be executed, and the parameters chosen in this example follow:
; Perform Direct Tension Tests
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'tt.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 0.1]
[tag += '_SR01']
program call 'tt.dat'
The test is performed twice, with different values of the prescribed strain-rate (1.0 and 0.1). The stress-strain responses are shown in the figures below.
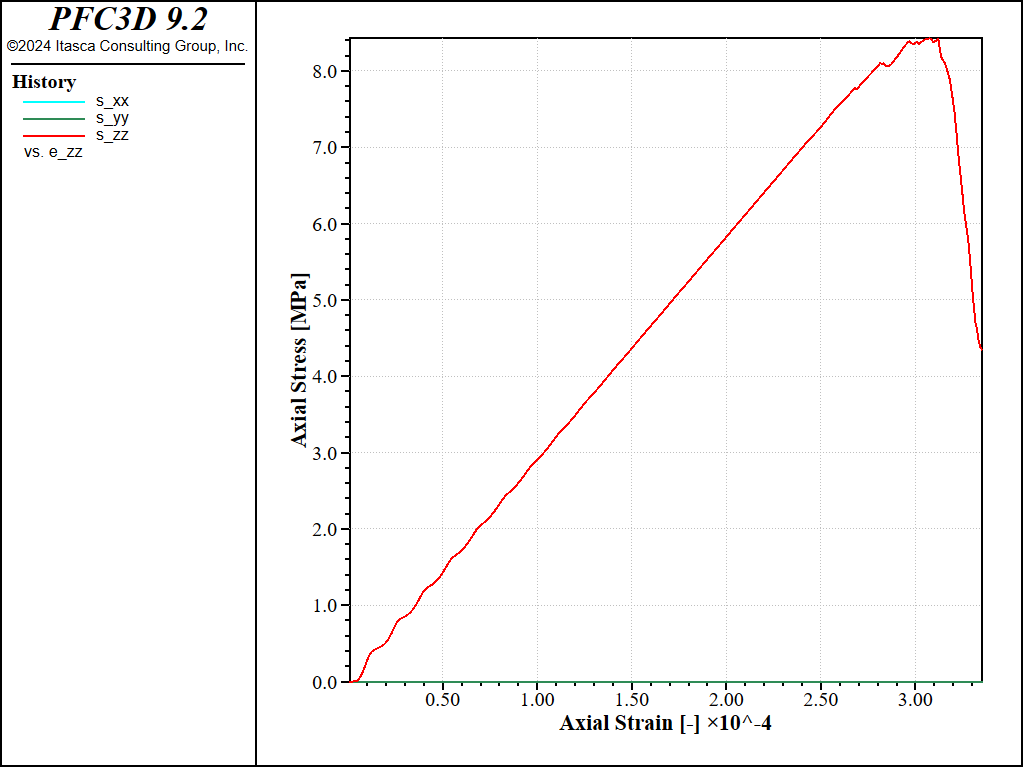
Figure 1: Stress vs Strain for a direct tension test with a strain rate of 1.0.
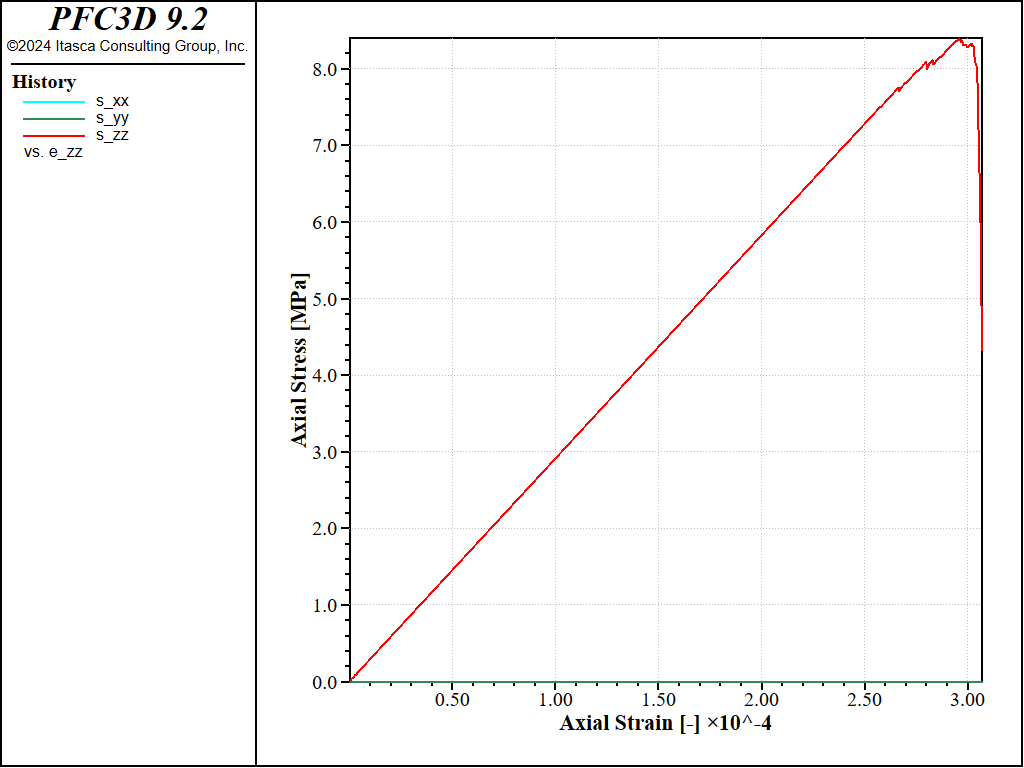
Figure 2: Stress vs Strain for a direct tension test with a strain rate of 0.1.
Both curves show the typical response of a brittle material, with a Young’s modulus of about 29GPa and a maximal tensile strength of about 8MPa in both cases. The strain rate has a small impact on the results: with the largest strain rate, the peak strength is slightly larger and reached at a slightly larger strain, with more pronounced oscillations at the beginning of the test.
Method 2: Using Domain Distortion
A similar test is performed by expanding the domain extent in the vertical direction. The file used to apply this test is tt2.dat, which is called by doall_A10.dat:
; Perform Direct Tension Test (using domain distortion)
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'tt2.dat'
The stress-strain curve obtained in this case (strain-rate of 1.0) is shown in the figure below. The response agrees quantitatively well with that obtained with the first method (Figure Figure #exa-sbnd-tt1)
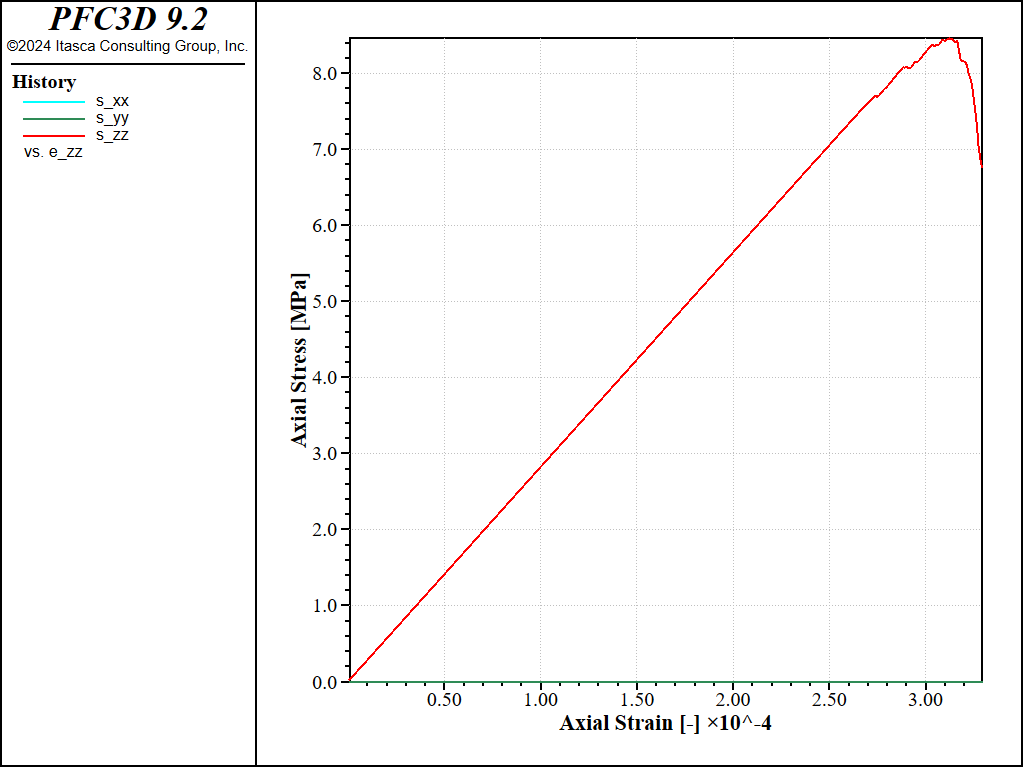
Figure 3: Stress vs Strain for a direct tension test with a strain rate of 1.0 (method 2).
Unconfined Compression Test
Two methods to simulate an unconfined compression test are described and compared below. The first method uses walls on the two opposite ends of the specimen in the vertical direction, and fixes their velocity. The second method distorts the domain inward in the vertical direction at a constant rate.
Method 1: Using Wall Platens
The file ucs.dat is used to perform the unconfined compression test using wall platens. It is partially parameterized for convenience, and the file doall_A10.dat demonstrates how it can be executed, and the parameters chosen in this example follow:
; Perform Unconfined Compression Test
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'ucs.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 0.1]
[tag += '_SR01']
program call 'ucs.dat'
The test is performed twice, with different values of the prescribed strain-rate (1.0 and 0.1). The stress-strain responses are shown in the figures below.
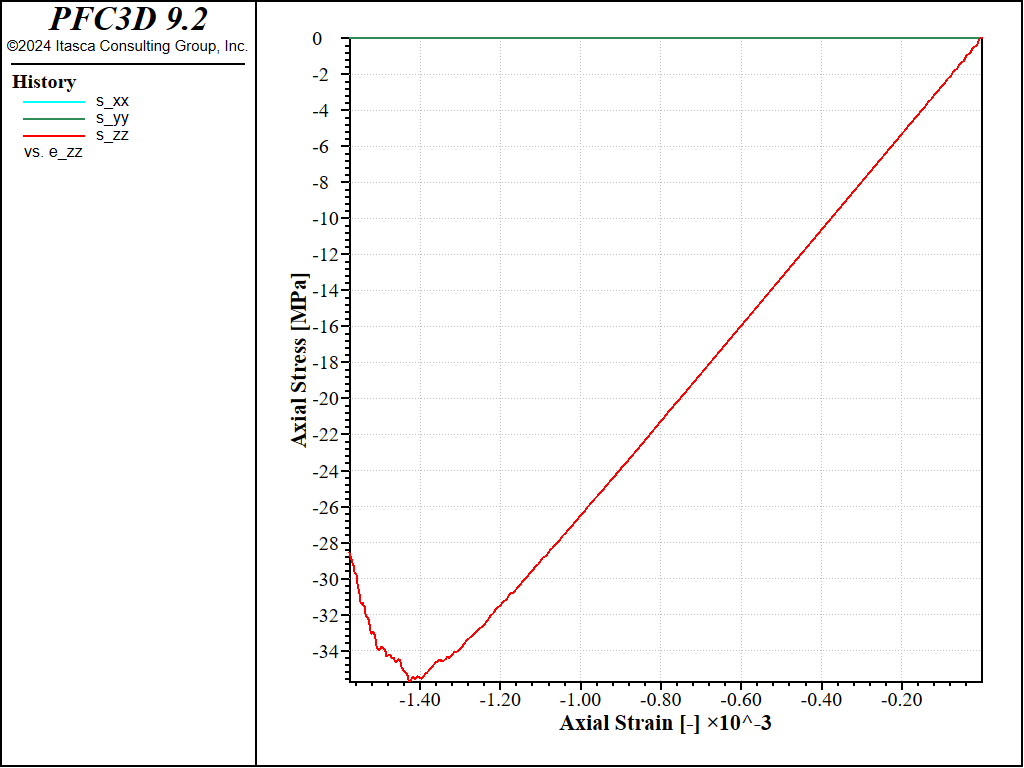
Figure 4: Stress vs Strain for an unconfined compression test with a strain rate of 1.0.
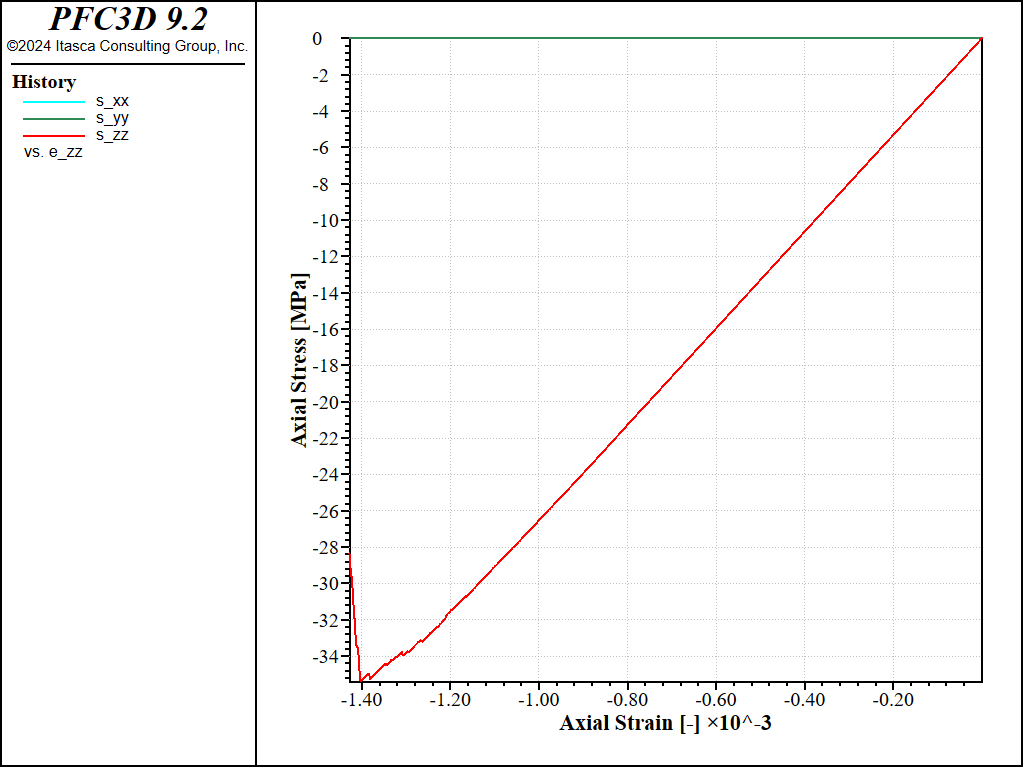
Figure 5: Stress vs Strain for an unconfined compression test with a strain rate of 0.1.
The peak compressive strength is about 32MPa, i.e. about 4 times the peak strength in tension, as typically observed for e.g. linear parallel-bonded models.
Method 2: Using Domain Distortion
A similar test is performed by contracting the domain extent in the vertical direction. The file used to apply this test is ucs2.dat, which is called by doall_A10.dat:
; Perform Unconfined Compression Test (using domain distortion)
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'ucs2.dat'
The stress-strain curve obtained in this case (strain-rate of 1.0) is shown in the figure below. The response agrees quantitatively well with that obtained with the first method (Figure 4)
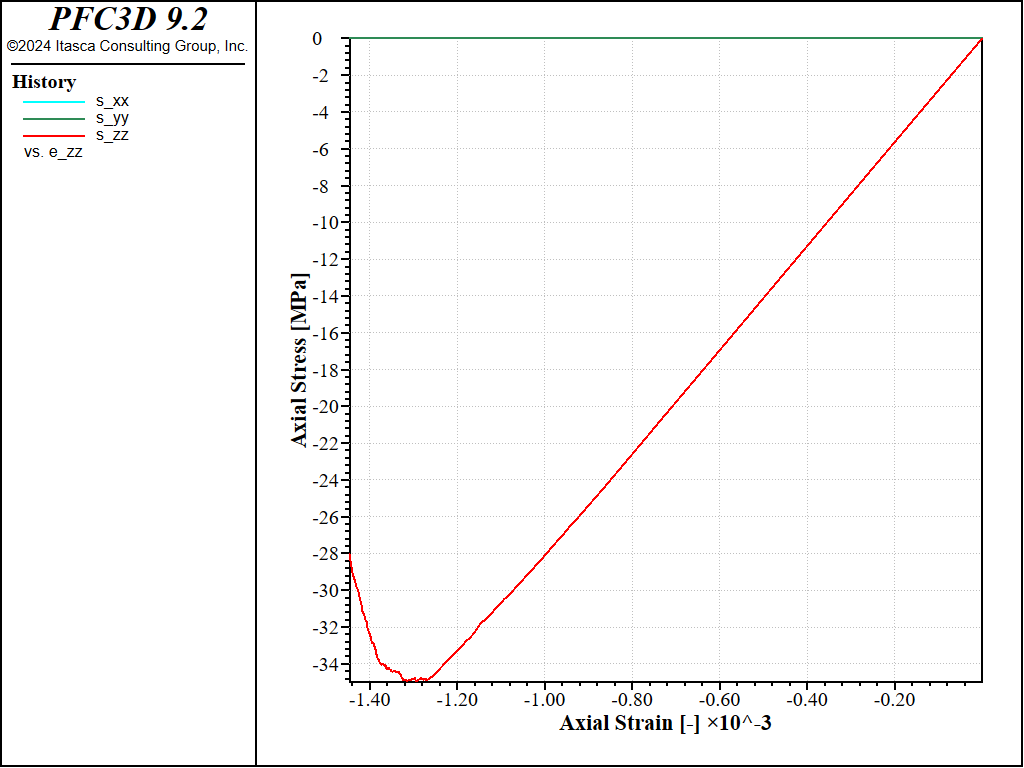
Figure 6: Stress vs Strain for an unconfined compression test with a strain rate of 1.0 (method 2).
Confined Compression Test
The file triax.dat is used to perform confined compression tests at various confining stress. It operates with periodic boundary conditions, and uses the servo-algorithm introduced above to apply the target confinement, then to maintain the lateral stress while contracting the specimen in the vertical direction at a constant strain-rate. It is partially parameterized for convenience, and the file doall_A10.dat demonstrates how it can be executed, and the parameters chosen in this example (strain-rate of 1.0 and a confining stress of 10kPa, 100kPa, 500kPa, 1MPa and 10MPa):
; Perform Confined Compression Tests
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -10.0e3]
[strain_rate = 1.0]
[tag = tag + '_P10_SR1']
program call 'triax.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -100.0e3]
[strain_rate = 1.0]
[tag = tag + '_P100_SR1']
program call 'triax.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -500.0e3]
[strain_rate = 1.0]
[tag = tag + '_P500_SR1']
program call 'triax.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -1000.0e3]
[strain_rate = 1.0]
[tag = tag + '_P1000_SR1']
program call 'triax.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -10000.0e3]
[strain_rate = 1.0]
[tag = tag + '_P10000_SR1']
program call 'triax.dat'
The stress-strain curves obtained are shown in the figure below, which shows a transition to a more ductile response at large confinement.
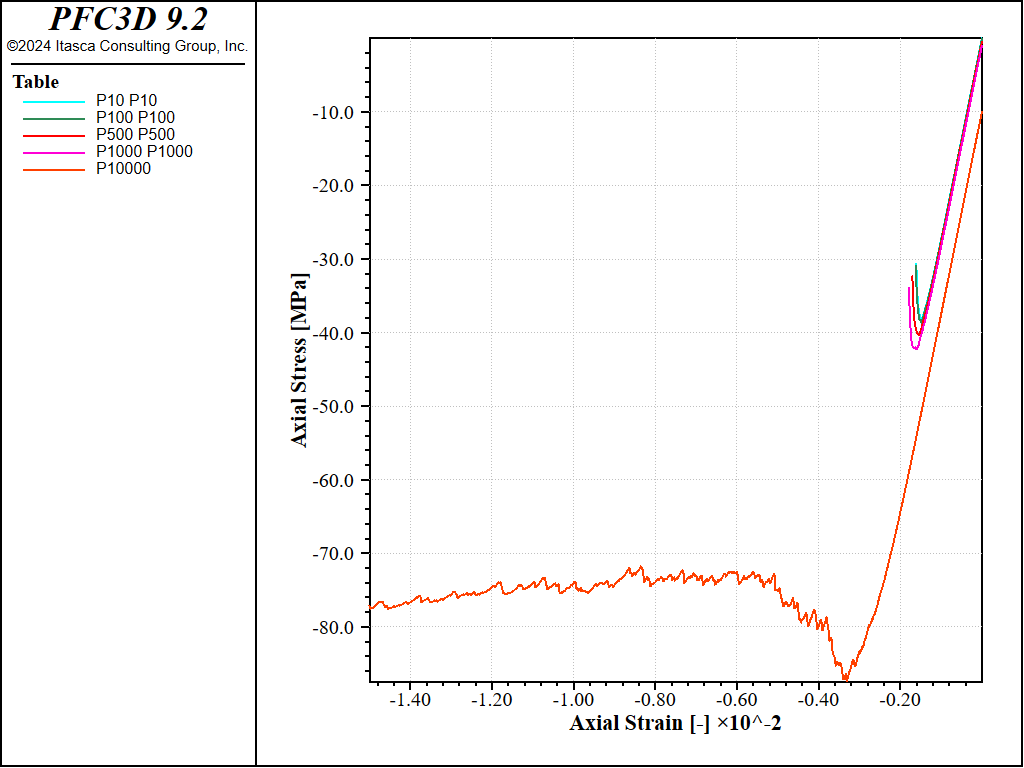
Figure 7: Stress vs Strain for an confined compression tests with a strain rate of 1.0 and increasing confinement.
Results and Discussion
The files discussed above demonstrate an effective set of procedures that can be used to generate a bonded-particle model, and perform direct-tension, unconfined compression and confined compression tests. In this example, the soft-bond contact model is used. The results shown above all use a set of parameters that forbid softening, and the resulting behavior has been shown to be that of a brittle material, with a compressive-to-tensile strength ratio of about 4.0, which is the value typically obtained with linear parallel-bonded materials, but is typically much low than the ratio most rocks exhibit.
A second set of tests is performed by executing the file doall_A10_S10_C0.dat. In this case, softening is activated by setting a value of 10.0 for the softening factor, and a value of 0.0 for the tensile strength softening factor. This means that once the tensile strength is reached at a specific contact, this contact enters a softening regime with a softening stiffness that is 1/10th of the loading stiffness, and breaks only if the tensile force reaches 0.0. The stress-strain curves obtained for a direct tension and unconfined compression tests are shown below.
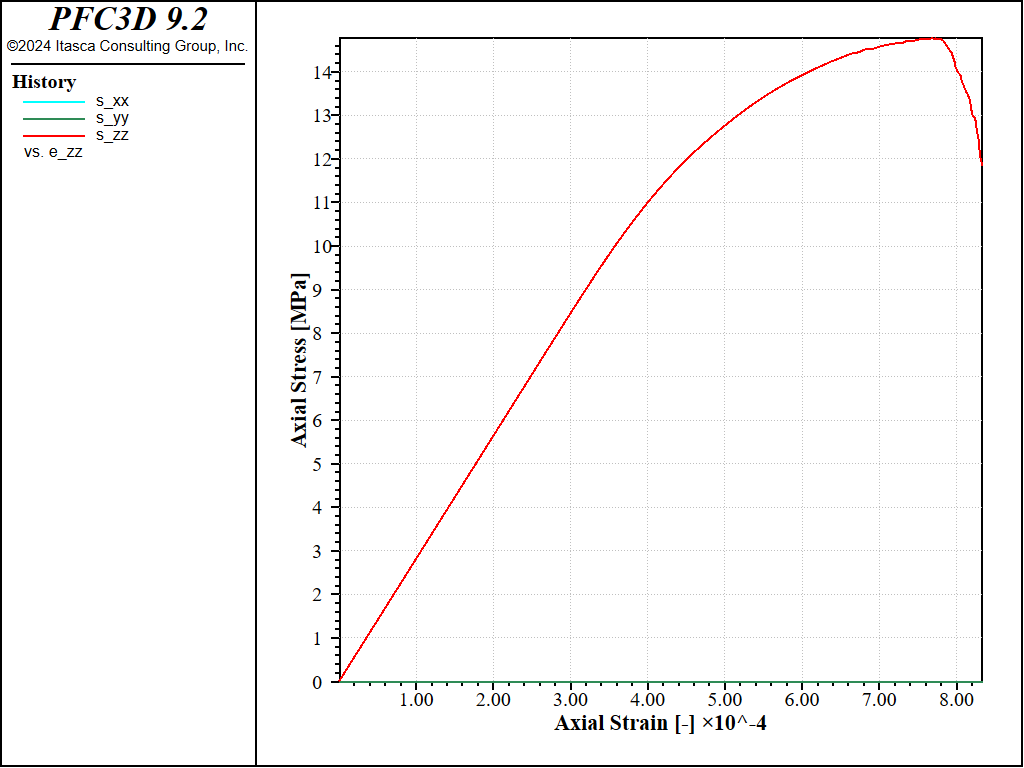
Figure 8: Stress vs Strain for a direct tension with a softening parameter of 10.
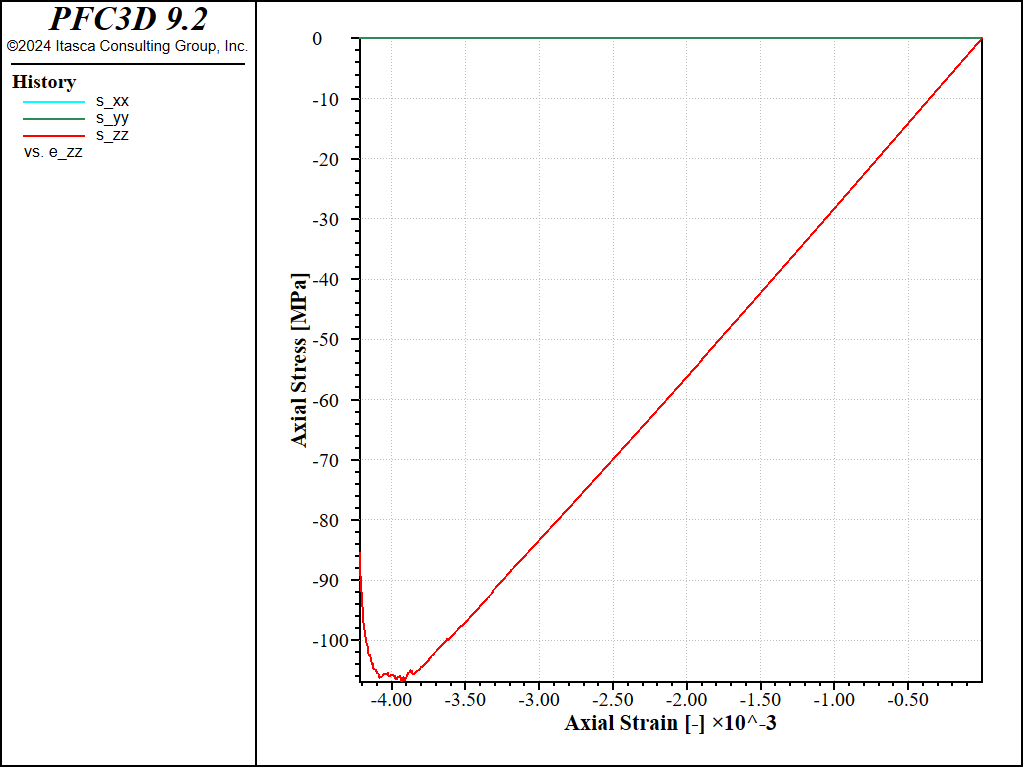
Figure 9: Stress vs Strain for an unconfined compression with a softening parameter of 10.
Under direct tension, the stress-strain curve exhibits a clear softening before reaching the peak strength, which is of about 14MPa (compared to 8MPa with no softening). Under compression, the peak strength is reached at about 100MPa, which leads to a compressive-to-tensile strength ratio of about 7.
A third set of tests is performed by executing the file doall_A10_S20_C0_COH1000.dat. In this case, softening is activated by setting a value of 20.0 for the softening factor, a value of 0.0 for the tensile strength softening factor, and the bond cohesion is increased to forbid shear failure.
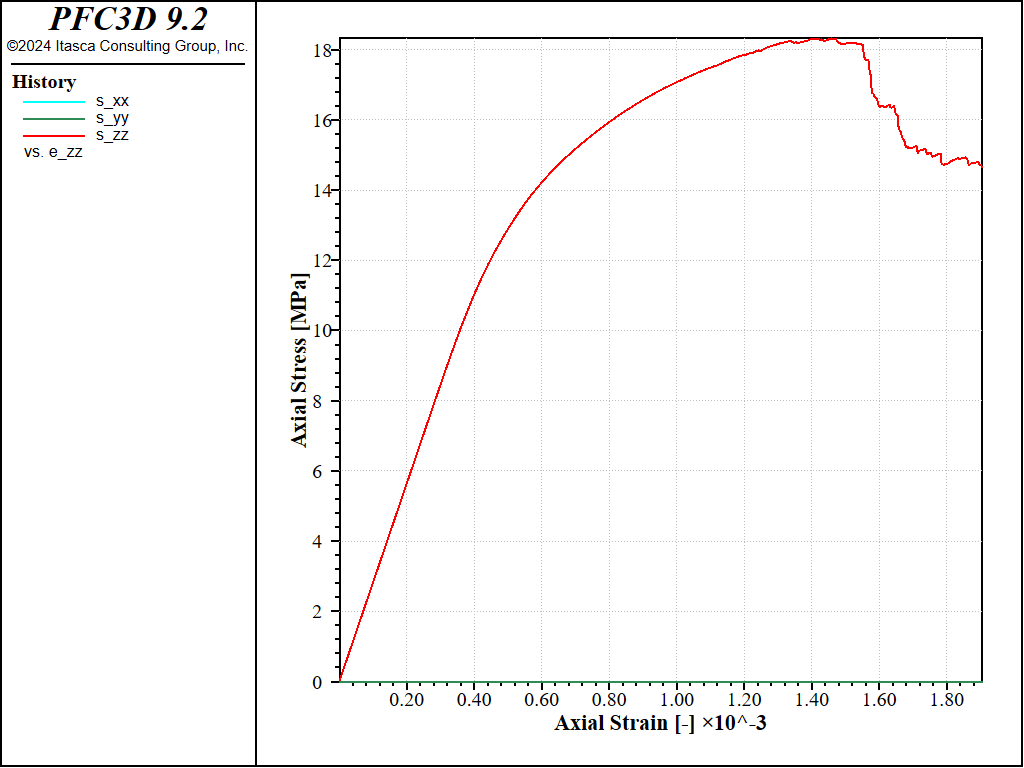
Figure 10: Stress vs Strain for a direct tension with a softening parameter of 20 and no shear failure allowed.
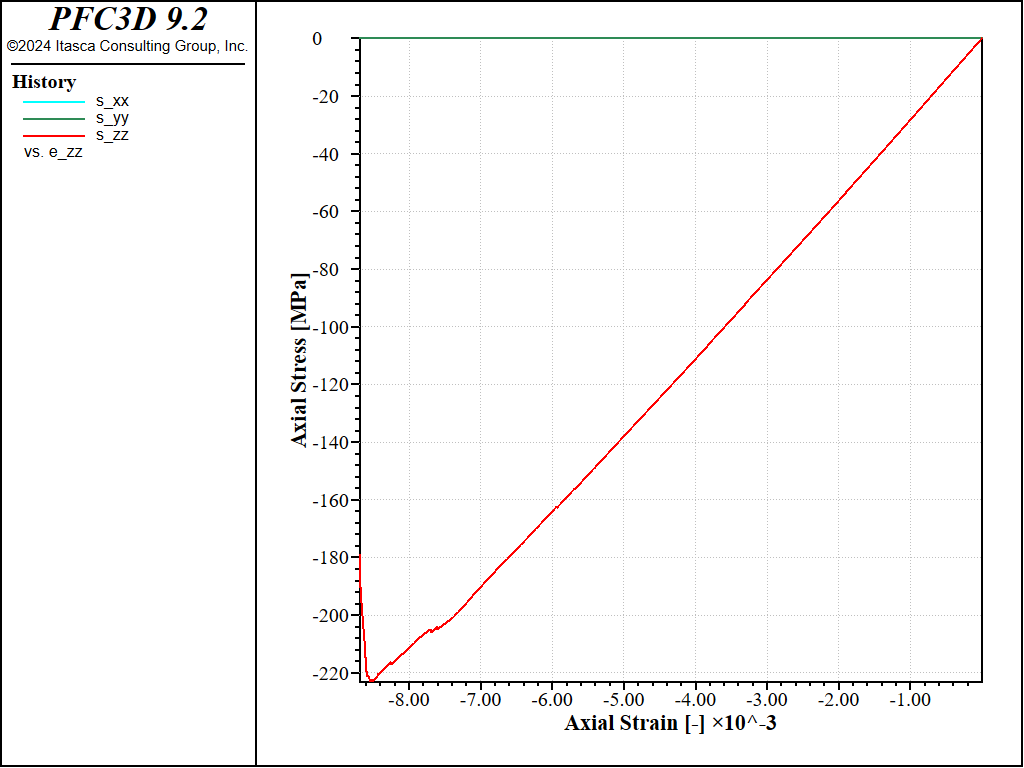
Figure 11: Stress vs Strain for an unconfined compression with a softening parameter of 20 and no shear failure allowed.
With these parameters, the peak strength increases to a value of about 200MPa in compression, and a value of about 17MPa in tension, i.e. a compressive-to-tensile strength ratio of about 12.0.
Data Files
doall_A10.dat
model new
model large-strain on
; excerpt-zmwu-start
; Generate packing
model random 10001
[resolution = 10] ; approx. number of balls accross specimen width
[davg = 2.5e-3] ; average ball diameter (m)
[dratio = 1.66] ; ball max/min diameter ratio [-]
[tag = 'A'+ string(resolution)]
program call 'make_brick.dat'
; excerpt-zmwu-end
; excerpt-webj-start
; Install contact model
model restore [string.build('brick_%1-iso',tag)]
[igap = 0.0*davg ]
[emod = 50.0e9 ]
[kratio = 2.5 ]
[fric = 0.5 ]
[ten_mean = 20.0e6 ]
[ten_std = 0.0e6 ]
[coh_mean = 100.0e6 ]
[coh_std = 0.0e6 ]
[soft = 0.0 ]
[cut = 1.0 ]
[tag += '_G0_E50_KR25_S0_C1']
program call 'bond_sb.dat'
; excerpt-webj-end
; excerpt-ebnh-start
; Perform Direct Tension Tests
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'tt.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 0.1]
[tag += '_SR01']
program call 'tt.dat'
; excerpt-ebnh-end
; excerpt-rfae-start
; Perform Unconfined Compression Test
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'ucs.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 0.1]
[tag += '_SR01']
program call 'ucs.dat'
; excerpt-rfae-end
; excerpt-pjoz-start
; Perform Direct Tension Test (using domain distortion)
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'tt2.dat'
; excerpt-pjoz-end
; excerpt-kmps-start
; Perform Unconfined Compression Test (using domain distortion)
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'ucs2.dat'
; excerpt-kmps-end
; excerpt-dbin-start
; Perform Confined Compression Tests
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -10.0e3]
[strain_rate = 1.0]
[tag = tag + '_P10_SR1']
program call 'triax.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -100.0e3]
[strain_rate = 1.0]
[tag = tag + '_P100_SR1']
program call 'triax.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -500.0e3]
[strain_rate = 1.0]
[tag = tag + '_P500_SR1']
program call 'triax.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -1000.0e3]
[strain_rate = 1.0]
[tag = tag + '_P1000_SR1']
program call 'triax.dat'
[tag = 'A10_G0_E50_KR25_S0_C1']
model restore [string.build('brick_%1-bonded',tag)]
[pc = -10000.0e3]
[strain_rate = 1.0]
[tag = tag + '_P10000_SR1']
program call 'triax.dat'
; excerpt-dbin-end
program return
doall_A10_S10_C0.dat
model new
[tag = 'A10']
model restore [string.build('brick_%1-iso',tag)]
; Install contact model
[igap = 0.0*davg ]
[emod = 50.0e9 ]
[kratio = 2.5 ]
[fric = 0.5 ]
[ten_mean = 20.0e6 ]
[ten_std = 0.0e6 ]
[coh_mean = 100.0e6 ]
[coh_std = 0.0e6 ]
[soft = 10.0 ]
[cut = 0.0 ]
[tag += '_G0_E50_KR25_S10_C0']
program call 'bond_sb.dat'
; Perform Direct Tension Test (using domain distortion)
[tag = 'A10_G0_E50_KR25_S10_C0']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'tt2.dat'
; Perform Unconfined Compression Test (using domain distortion)
[tag = 'A10_G0_E50_KR25_S10_C0']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'ucs2.dat'
program return
doall_A10_S20_C0_COH1000.dat
model new
[tag = 'A10']
model restore [string.build('brick_%1-iso',tag)]
; Install contact model
[igap = 0.0*davg ]
[emod = 50.0e9 ]
[kratio = 2.5 ]
[fric = 0.5 ]
[ten_mean = 20.0e6 ]
[ten_std = 0.0e6 ]
[coh_mean = 100.0e7 ]
[coh_std = 0.0e6 ]
[soft = 20.0 ]
[cut = 0.0 ]
[tag += '_G0_E50_KR25_S20_C0_COH1000']
program call 'bond_sb.dat'
; Perform Direct Tension Test (using domain distortion)
[tag = 'A10_G0_E50_KR25_S20_C0_COH1000']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'tt2.dat'
; Perform Unconfined Compression Test (using domain distortion)
[tag = 'A10_G0_E50_KR25_S20_C0_COH1000']
model restore [string.build('brick_%1-bonded',tag)]
[strain_rate = 1.0]
[tag += '_SR1']
program call 'ucs2.dat'
program return
make_brick.dat
; filename: make_brick.dat
;
; Generate an isotropic, homogeneous assembly of balls with periodic
; boundary conditions, and settle under low isotropic confinement
; using a servo-control algorithm to distort the periodic domain
;
; ===================================================================
; Setup domain extent (aspect ratio 2:1) and boundary conditions
model domain extent [-0.5*resolution*davg] [0.5*resolution*davg] ...
[-0.5*resolution*davg] [0.5*resolution*davg] ...
[-1.0*resolution*davg] [1.0*resolution*davg] ...
condition periodic
; Distribute balls to a target low porosity and set density and
; local damping attributes
[dmin = 2.0*davg / (1.0 + dratio)]
[dmax = dmin * dratio]
ball distribute porosity 0.36 radius [0.5*dmin] [0.5*dmax]
ball attribute density 2000.0 damp 0.7
; Choose the contact model
contact cmat default model linear ...
method deformability emod 1e8 kratio 2.5
; Monitoring
model history name 'ratio-average' mechanical ratio-average
model history name 'timestep' timestep
; Perform some initial cycles and periodically reset the
; spin and velocities to zero to relax the inital overlaps,
; then solve to equilibrium
model cycle 1000 calm 100
model solve ratio-average 5e-3
model save [string.build('brick_%1-pkg',tag)]
; Use a servo-control algorithm to settle the assembly under
; a presecribed low isotropic stress state
; Parameter definitions (used by the servo-control function)
[servo_do_z = true ]
[servo_ts_xx = -1.0e5 ]
[servo_ts_yy = -1.0e5 ]
[servo_ts_zz = -1.0e5 ]
[servo_gain = 1.0e-4 ]
[servo_tol = 1e-2]
[s_xx = 0.0]
[s_yy = 0.0]
[s_zz = 0.0]
[Lx = domain.max.x() - domain.min.x()]
[Ly = domain.max.y() - domain.min.y()]
[Lz = domain.max.z() - domain.min.z()]
measure create id 1 radius [0.95*0.5*Lx]
; Load utility functions
program call 'servo.fis' suppress
; Monitoring
fish history name 's_xx' s_xx
fish history name 's_yy' s_yy
fish history name 's_zz' s_zz
fish history name 'L_x' Lx
fish history name 'L_y' Ly
fish history name 'L_z' Lz
model domain tolerance 1e-3
model solve fish-call 1.0 servo_domain ...
fish-halt servo_halt ...
ratio-average 1e-3 ...
cycles 100 and
model save [string.build('brick_%1-iso',tag)]
; ===================================================================
program return
; EOF: make_brick.dat
servo.fis
; filename: servo.fis
;
; Utility function to define a servo-control algorithm
; to distort the periodic domain to apply a target confinement
;
; ===================================================================
fish define servo_domain
global Lx = domain.max.x() - domain.min.x()
global Ly = domain.max.y() - domain.min.y()
global Lz = domain.max.z() - domain.min.z()
local vol = Lx*Ly*Lz
local m = measure.find(1)
local mr = math.sqrt((0.5*Lx)^2+(0.5*Ly)^2+(0.5*Lz)^2)
local mv = (4.0/3.0)*math.pi*mr^3
measure.radius(m) = mr
local stress = measure.stress(m) *mv/vol
global s_xx = stress(1,1)
global servo_xdiff = servo_ts_xx - s_xx
global servo_xrate = servo_gain *servo_xdiff
domain.strain.rate.xx = servo_xrate
global s_yy = stress(2,2)
global servo_ydiff = servo_ts_yy - s_yy
global servo_yrate = servo_gain *servo_ydiff
domain.strain.rate.yy = servo_yrate
global s_zz = stress(3,3)
if servo_do_z then
global servo_zdiff = servo_ts_zz - s_zz
global servo_zrate = servo_gain * servo_zdiff
endif
domain.strain.rate.zz = servo_zrate
end
fish define servo_halt
servo_halt = false
local delta = math.max(math.abs(servo_xdiff/servo_ts_xx) ...
,math.abs(servo_ydiff/servo_ts_yy))
if servo_do_z then
delta = math.max(math.abs(servo_zdiff/servo_ts_zz),delta)
endif
if delta < servo_tol then
servo_halt = true
domain.strain.rate.xx = 0.0
domain.strain.rate.yy = 0.0
domain.strain.rate.zz = 0.0
endif
end
; ===================================================================
program return
; EOF: servo.fis
bond_sb.dat
ball attribute force-contact multiply 0.0 ...
moment-contact multiply 0.0 ...
velocity multiply 0.0 ...
spin multiply 0.0 ...
displacement multiply 0.0
contact cmat default model 'softbond' ...
method deformability emod [emod] kratio [kratio] ...
property fric [fric] sb_mode 1 ...
sb_soft [soft] sb_cut [cut]
contact cmat proximity [igap]
model clean all
contact cmat apply
fish define normal_dist(c,mean,sdev)
; Compute a non-negative value from a normal distribution with
; given mean and standard deviation.
;
loop while 1 # 0
local _val = mean + (math.random.gauss * sdev)
if _val >= 0.0 then
normal_dist = _val
exit
end_if
end_loop
end
contact property sb_coh normal_dist([coh_mean],[coh_std])
contact property sb_ten normal_dist([ten_mean],[ten_std])
model save [string.build('brick_%1-bonded',tag)]
tt.dat
fish define setup_tt
; identify boundary balls
loop foreach local c contact.list.all
if contact.offset.z(c) # 0 then
ball.group(contact.end1(c)) = 'boundary'
ball.group(contact.end2(c)) = 'boundary'
endif
endloop
; install measurement sphere
Lx0 = domain.max.x() - domain.min.x()
Ly0 = domain.max.y() - domain.min.y()
Lz0 = domain.max.z() - domain.min.z()
local mr = 0.5*math.min(Lx0,Ly0,Lz0)
measure.radius(measure.find(1)) = 0.9*mr
global btop = ball.near(0.0,0.0,domain.max.z())
global bbot = ball.near(0.0,0.0,domain.min.z())
ball.group(btop,'gage') = 'top'
ball.group(bbot,'gage') = 'bot'
global bright = ball.near(domain.max.x(),0.0,0.0)
global bleft = ball.near(domain.min.x(),0.0,0.0)
global bfront = ball.near(0.0,domain.max.y(),0.0)
global bback = ball.near(0.0,domain.min.y(),0.0)
ball.group(bright,'gage') = 'right'
ball.group(bleft,'gage') = 'left'
ball.group(bfront,'gage') = 'front'
ball.group(bback,'gage') = 'back'
Lx0 = ball.pos.x(bright) - ball.pos.x(bleft)
Ly0 = ball.pos.y(bfront) - ball.pos.y(bback)
Lz0 = ball.pos.z(btop) - ball.pos.z(bbot)
; enlarge domain extent
domain.min.x = 1.5*domain.min.x
domain.max.x = 1.5*domain.max.x
domain.min.y = 1.5*domain.min.y
domain.max.y = 1.5*domain.max.y
domain.min.z = 1.5*domain.min.z
domain.max.z = 1.5*domain.max.z
end
[setup_tt]
model domain condition stop
model clean all
contact method bond gap [igap] range contact all
; reset the proximity, delete inactive contacts
; and clean the model to reduce the number of inactive contacts
contact cmat proximity 0.0
contact delete range contact inactive
model clean all
ball fix velocity spin range group 'boundary'
;contact property sb_ten 1e20 sb_coh 1e20 range group 'boundary' matches 1
fish define e_xx
Lx = ball.pos.x(bright) - ball.pos.x(bleft)
e_xx = (Lx - Lx0) / Lx0
end
fish define e_yy
Ly = ball.pos.y(bfront) - ball.pos.y(bback)
e_yy = (Ly - Ly0) / Ly0
end
fish define e_zz
Lz = ball.pos.z(btop) - ball.pos.z(bbot)
e_zz = (Lz - Lz0) / Lz0
end
fish define e_zz
Lz = ball.pos.z(btop) - ball.pos.z(bbot)
e_zz = (Lz - Lz0) / Lz0
end
model cycle 1
[s_xx = measure.stress.xx(measure.find(1))]
[s_yy = measure.stress.yy(measure.find(1))]
[s_zz = measure.stress.zz(measure.find(1))]
fish define s_zz
s_zz = measure.stress.zz(measure.find(1))
end
fish define poiss_ratio
poiss_ratio = - 0.5*(e_xx+e_yy) / e_zz
end
fish define emod_secant
emod_secant = s_zz / e_zz
end
history purge
fish history name 'e_xx' e_xx
fish history name 'e_yy' e_yy
fish history name 'e_zz' e_zz
fish history name 'emod_secant' emod_secant
fish history name 'poiss_ratio' poiss_ratio
[peak_frac = 0.5 ]
fish define halt
halt = false
global s_zz_max = math.max(s_zz,s_zz_max)
if s_zz < peak_frac*s_zz_max
halt = 1
endif
end
ball attribute velocity-z [ 0.5*strain_rate*Lz0] ...
range position-z 0.0 [Lz0] ...
group 'boundary'
ball attribute velocity-z [-0.5*strain_rate*Lz0] ...
range position-z [-Lz0] 0.0 ...
group 'boundary'
model save [string.build('tt_%1-initial',tag)]
model solve fish-halt halt ...
cycles 100 and
model save [string.build('tt_%1-final',tag)]
; ===================================================================
program return
;EOF
ucs.dat
fish define setup_ucs
; identify boundary balls
loop foreach local c contact.list.all
if contact.offset.z(c) # 0 then
ball.group(contact.end1(c)) = 'boundary'
ball.group(contact.end2(c)) = 'boundary'
endif
endloop
global zmax = 0.0
global zmin = 0.0
local cntmax = 0
local cntmin = 0
loop foreach local b ball.groupmap('boundary')
local z = ball.pos.z(b)
if z > 0.0 then
zmax += z + ball.radius(b)
cntmax +=1
else
zmin += z - ball.radius(b)
cntmin +=1
endif
endloop
zmax /= cntmax
zmin /= cntmin
; install measurement sphere
Lx0 = domain.max.x() - domain.min.x()
Ly0 = domain.max.y() - domain.min.y()
Lz0 = domain.max.z() - domain.min.z()
global mr = 0.5*math.min(Lx0,Ly0,Lz0)
measure.radius(measure.find(1)) = 0.9*mr
global bright = ball.near(domain.max.x(),0.0,0.0)
global bleft = ball.near(domain.min.x(),0.0,0.0)
global bfront = ball.near(0.0,domain.max.y(),0.0)
global bback = ball.near(0.0,domain.min.y(),0.0)
ball.group(bright,'gage') = 'right'
ball.group(bleft,'gage') = 'left'
ball.group(bfront,'gage') = 'front'
ball.group(bback,'gage') = 'back'
Lx0 = ball.pos.x(bright) - ball.pos.x(bleft)
Ly0 = ball.pos.y(bfront) - ball.pos.y(bback)
; enlarge domain extent
domain.min.x = 1.5*domain.min.x
domain.max.x = 1.5*domain.max.x
domain.min.y = 1.5*domain.min.y
domain.max.y = 1.5*domain.max.y
domain.min.z = 1.5*domain.min.z
domain.max.z = 1.5*domain.max.z
;
end
[setup_ucs]
model domain condition stop
model clean all
contact method bond gap [igap] range contact all
; reset the proximity, delete inactive contacts
; and clean the model to reduce the number of inactive contacts
contact cmat proximity 0.0
contact delete range contact inactive
model clean all
wall generate name 'box' box [-0.5*Lx0] [0.5*Lx0] ...
[-0.5*Ly0] [0.5*Ly0] ...
[-0.5*Lz0] [0.5*Lz0] ...
expand 1.25
wall delete range set name 'boxLeft'
wall delete range set name 'boxRight'
wall delete range set name 'boxFront'
wall delete range set name 'boxBack'
contact cmat default type 'ball-facet' ...
model softbond ...
method deformability emod [emod] kratio [kratio] ...
property sb_mode 1 fric [fric]
model clean all
[wtop = wall.find('boxTop')]
[wbot = wall.find('boxBottom')]
[Lz0 = wall.pos.z(wtop) - wall.pos.z(wbot)]
fish define e_xx
Lx = ball.pos.x(bright) - ball.pos.x(bleft)
e_xx = (Lx - Lx0) / Lx0
end
fish define e_yy
Ly = ball.pos.y(bfront) - ball.pos.y(bback)
e_yy = (Ly - Ly0) / Ly0
end
fish define e_zz
Lz = wall.pos.z(wtop) - wall.pos.z(wbot)
e_zz = (Lz - Lz0) / Lz0
end
model cycle 1
[s_xx = measure.stress.xx(measure.find(1))]
[s_yy = measure.stress.yy(measure.find(1))]
[s_zz = measure.stress.zz(measure.find(1))]
fish define s_zz
s_zz = measure.stress.zz(measure.find(1))
end
fish define poiss_ratio
poiss_ratio = - 0.5*(e_xx+e_yy) / e_zz
end
fish define emod_secant
emod_secant = s_zz / e_zz
end
history purge
fish history name 'e_xx' e_xx
fish history name 'e_yy' e_yy
fish history name 'e_zz' e_zz
fish history name 'emod_secant' emod_secant
fish history name 'poiss_ratio' poiss_ratio
[peak_frac = 0.8 ]
fish define halt
halt = false
global s_zz_min = math.min(s_zz,s_zz_min)
if s_zz > peak_frac*s_zz_min
halt = 1
endif
end
wall attribute velocity-z [-0.5*strain_rate*Lz0] range set name 'boxTop'
wall attribute velocity-z [ 0.5*strain_rate*Lz0] range set name 'boxBottom'
model save [string.build('ucs_%1-initial',tag)]
[peak_frac = 0.8 ]
model solve fish-halt halt ...
cycles 100 and
model save [string.build('ucs_%1-final',tag)]
; ===================================================================
program return
;EOF
tt2.dat
fish define setup_tt
; identify boundary balls
loop foreach local c contact.list.all
if contact.offset.z(c) # 0 then
ball.group(contact.end1(c)) = 'boundary'
ball.group(contact.end2(c)) = 'boundary'
endif
endloop
; install measurement sphere
Lx0 = domain.max.x() - domain.min.x()
Ly0 = domain.max.y() - domain.min.y()
Lz0 = domain.max.z() - domain.min.z()
local mr = 0.5*math.min(Lx0,Ly0,Lz0)
measure.radius(measure.find(1)) = 0.9*mr
global btop = ball.near(0.0,0.0,domain.max.z())
global bbot = ball.near(0.0,0.0,domain.min.z())
global bright = ball.near(domain.max.x(),0.0,0.0)
global bleft = ball.near(domain.min.x(),0.0,0.0)
global bfront = ball.near(0.0,domain.max.y(),0.0)
global bback = ball.near(0.0,domain.min.y(),0.0)
ball.group(bright,'gage') = 'right'
ball.group(bleft,'gage') = 'left'
ball.group(bfront,'gage') = 'front'
ball.group(bback,'gage') = 'back'
ball.group(btop,'gage') = 'top'
ball.group(bbot,'gage') = 'bot'
Lx0 = ball.pos.x(bright) - ball.pos.x(bleft)
Ly0 = ball.pos.y(bfront) - ball.pos.y(bback)
Lz0 = ball.pos.z(btop) - ball.pos.z(bbot)
; enlarge domain extent
domain.min.x = 1.5*domain.min.x
domain.max.x = 1.5*domain.max.x
domain.min.y = 1.5*domain.min.y
domain.max.y = 1.5*domain.max.y
domain.min.z = 1.5*domain.min.z
domain.max.z = 1.5*domain.max.z
end
[setup_tt]
model domain condition stop
model clean all
contact method bond gap [igap] range contact all
; reset the proximity, delete inactive contacts
; and clean the model to reduce the number of inactive contacts
contact cmat proximity 0.0
contact delete range contact inactive
model clean all
ball fix velocity-z range group 'boundary'
fish define e_xx
Lx = ball.pos.x(bright) - ball.pos.x(bleft)
e_xx = (Lx - Lx0) / Lx0
end
fish define e_yy
Ly = ball.pos.y(bfront) - ball.pos.y(bback)
e_yy = (Ly - Ly0) / Ly0
end
fish define e_zz
Lz = ball.pos.z(btop) - ball.pos.z(bbot)
e_zz = (Lz - Lz0) / Lz0
end
model cycle 1
[s_xx = measure.stress.xx(measure.find(1))]
[s_yy = measure.stress.yy(measure.find(1))]
[s_zz = measure.stress.zz(measure.find(1))]
fish define s_zz
s_zz = measure.stress.zz(measure.find(1))
end
fish define poiss_ratio
poiss_ratio = - 0.5*(e_xx+e_yy) / e_zz
end
fish define emod_secant
emod_secant = s_zz / e_zz
end
history purge
fish history name 'e_xx' e_xx
fish history name 'e_yy' e_yy
fish history name 'e_zz' e_zz
fish history name 'emod_secant' emod_secant
fish history name 'poiss_ratio' poiss_ratio
[peak_frac = 0.8 ]
fish define halt
halt = false
global s_zz_max = math.max(s_zz,s_zz_max)
if s_zz < peak_frac*s_zz_max
halt = 1
endif
end
model domain strain-rate-zz [strain_rate]
[peak_frac = 0.8 ]
model save [string.build('tt2_%1-initial',tag)]
model solve fish-halt halt ...
cycles 100 and
model save [string.build('tt2_%1-final',tag)]
; ===================================================================
program return
;EOF
ucs2.dat
fish define setup_tt
; identify boundary balls
loop foreach local c contact.list.all
if contact.offset.z(c) # 0 then
ball.group(contact.end1(c)) = 'boundary'
ball.group(contact.end2(c)) = 'boundary'
endif
endloop
; install measurement sphere
Lx0 = domain.max.x() - domain.min.x()
Ly0 = domain.max.y() - domain.min.y()
Lz0 = domain.max.z() - domain.min.z()
local mr = 0.5*math.min(Lx0,Ly0,Lz0)
measure.radius(measure.find(1)) = 0.9*mr
global bright = ball.near(domain.max.x(),0.0,0.0)
global bleft = ball.near(domain.min.x(),0.0,0.0)
global bfront = ball.near(0.0,domain.max.y(),0.0)
global bback = ball.near(0.0,domain.min.y(),0.0)
global btop = ball.near(0.0,0.0,domain.max.z())
global bbot = ball.near(0.0,0.0,domain.min.z())
ball.group(bright ,'gage') = 'right'
ball.group(bleft ,'gage') = 'left'
ball.group(bfront ,'gage') = 'front'
ball.group(bback ,'gage') = 'back'
ball.group(btop ,'gage') = 'top'
ball.group(bbot ,'gage') = 'bot'
; enlarge domain extent
domain.min.x = 1.5*domain.min.x
domain.max.x = 1.5*domain.max.x
domain.min.y = 1.5*domain.min.y
domain.max.y = 1.5*domain.max.y
domain.min.z = 1.5*domain.min.z
domain.max.z = 1.5*domain.max.z
;
Lx0 = ball.pos.x(bright) - ball.pos.x(bleft)
Ly0 = ball.pos.y(bfront) - ball.pos.y(bback)
Lz0 = ball.pos.z(btop) - ball.pos.z(bbot)
end
[setup_tt]
model domain condition stop
model clean all
contact method bond gap [igap] range contact all
; reset the proximity, delete inactive contacts
; and clean the model to reduce the number of inactive contacts
contact cmat proximity 0.0
contact delete range contact inactive
model clean all
model cycle 1
[s_xx = measure.stress.xx(measure.find(1))]
[s_yy = measure.stress.yy(measure.find(1))]
[s_zz = measure.stress.zz(measure.find(1))]
ball fix velocity-z range group 'boundary'
fish define e_xx
Lx = ball.pos.x(bright) - ball.pos.x(bleft)
e_xx = (Lx - Lx0) / Lx0
end
fish define e_yy
Ly = ball.pos.y(bfront) - ball.pos.y(bback)
e_yy = (Ly - Ly0) / Ly0
end
fish define e_zz
Lz = ball.pos.z(btop) - ball.pos.z(bbot)
e_zz = (Lz - Lz0) / Lz0
end
fish define poiss_ratio
poiss_ratio = - 0.5*(e_xx+e_yy) / e_zz
end
fish define emod_secant
emod_secant = s_zz / e_zz
end
history purge
fish history name 'e_xx' e_xx
fish history name 'e_yy' e_yy
fish history name 'e_zz' e_zz
fish history name 'emod_secant' emod_secant
fish history name 'poiss_ratio' poiss_ratio
fish define s_zz
s_zz = measure.stress.zz(measure.find(1))
end
[peak_frac = 0.8]
fish define halt
halt = false
global s_zz_min = math.min(s_zz,s_zz_min)
if s_zz > peak_frac*s_zz_min
halt = 1
endif
end
model domain strain-rate-zz [-strain_rate]
[peak_frac = 0.8]
model save [string.build('ucs2_%1-initial',tag)]
model solve fish-halt halt ...
cycles 100 and
model save [string.build('ucs2_%1-final',tag)]
; ===================================================================
program return
;EOF
triax.dat
contact method bond gap [igap] range contact all
contact cmat proximity 0.0
contact delete range contact inactive
model clean all
; Bring to istotropic confinement
[Lx0 = domain.max.x() - domain.min.x()]
[Ly0 = domain.max.y() - domain.min.y()]
[Lz0 = domain.max.z() - domain.min.z()]
fish define e_xx
Lx = domain.max.x() - domain.min.x()
e_xx = (Lx - Lx0) / Lx0
end
fish define e_yy
Ly = domain.max.y() - domain.min.y()
e_yy = (Ly - Ly0) / Ly0
end
fish define e_zz
Lz = domain.max.z() - domain.min.z()
e_zz = (Lz - Lz0) / Lz0
end
model cycle 1
history purge
fish history name 'e_xx' e_xx
fish history name 'e_yy' e_yy
fish history name 'e_zz' e_zz
[servo_do_z = true ]
[servo_ts_xx = pc ]
[servo_ts_yy = pc ]
[servo_ts_zz = pc ]
[servo_gain = 1.0e-5 ]
[servo_tol = 1.0e-5 ]
model solve fish-call 1.0 servo_domain ...
fish-halt servo_halt ...
ratio-average 1e-5 ...
cycles 100 and
model save [string.build('triax_%1-iso',tag)]
; perform compression
history purge
[servo_do_z = false ]
[servo_zrate = -strain_rate]
[servo_gain = 1.0e-5 ]
[Lx0 = domain.max.x() - domain.min.x()]
[Ly0 = domain.max.y() - domain.min.y()]
[Lz0 = domain.max.z() - domain.min.z()]
fish define emod_secant
emod_secant = (s_zz - 0.5*(s_xx+s_yy)) / e_zz
end
fish define poiss_ratio
poiss_ratio = - 0.5*(e_xx+e_yy) / e_zz
end
fish history name 'emod_secant' emod_secant
fish history name 'poiss_ratio' poiss_ratio
[emax = 2.0e-4]
fish define halt
halt = false
if e_zz < -emax
halt = 1
endif
end
[emax = 2.0e-4]
model solve fish-call 1.0 servo_domain ...
fish-halt halt ...
cycles 100 and
[ymod = (s_zz - 0.5*(s_xx+s_yy)) / e_zz]
[poiss = - 0.5*(e_xx+e_yy) / e_zz]
model save [string.build('triax_%1-elastic',tag)]
[peak_frac = 0.8 ]
fish define halt
halt = false
global s_zz_min = math.min(s_zz,s_zz_min)
if s_zz > peak_frac*s_zz_min
halt = 1
exit
endif
if e_zz < -emax
halt = 1
exit
endif
end
[emax = 15.0e-3]
[peak_frac = 0.8 ]
model solve fish-call 1.0 servo_domain ...
fish-halt halt ...
cycles 100 and
model save [string.build('triax_%1-final',tag)]
; ===================================================================
program return
;EOF
Endnote
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Dec 19, 2024 |
