One-Dimensional Explosive-Rock Interaction

Note

The project file for this example is available to be viewed/run in FLAC2D. The project’s main data files are shown at the end of this example.

Problem Statement

This example illustrates the application of the Jones-Wilkins-Lee (JWL) equation of state to analyze the explosive-rock interaction near a cylindrical charge geometry. It builds upon the Single-Zone JWL Pressurization example, extending the analysis to explicity model the surrounding rock as an elastoplastic medium.

The interaction between explosives and rock is a dynamic process involving transfer of energy into the rock, leading to a sequence of mechanical responses including crushing, fracturing, fragmentation, and vibrations (Figure 1). Detonation of explosives induces stress waves that propagate radially into the surrounding rock. The stress waves quickly attenuate with distance, transitioning from a high amplitude compressive wave (crushed zone) to a lower amplitude tensile wave (fractured zone). The transition between the two zones is largely controlled by the rock’s mechancial properties and the explosive type. Beyond the initial tensile fracturing zone, the rock breaks down into discrete fragments. The size distribution of the fragments is often modeled using empirical relationships that depend on rock properties, explosive properties, and geometrical parameters, e.g., Kuz-Ram.

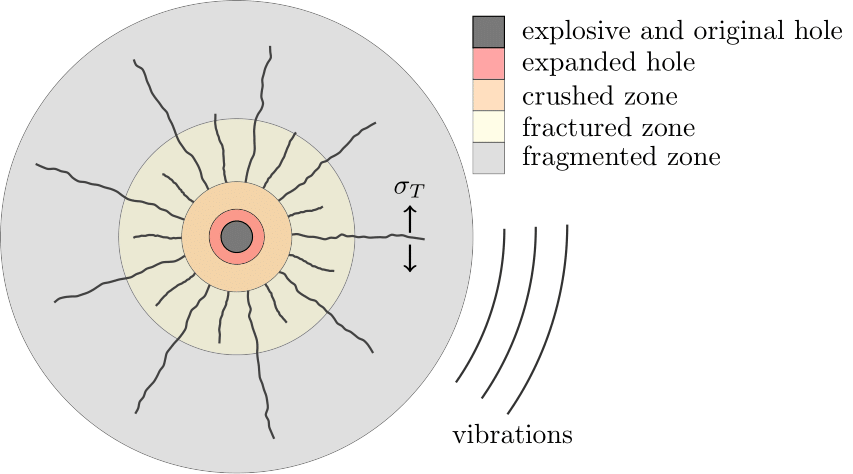
Figure 1: Illustration of blasting induced rock crushing and fragmentation. The symbol \(\sigma_T\) refers to tensile hoop stress induced by large compressive stresses in the crushed zone.

This example approximates a one-dimensional radial response around a cylindrical charge explosive using a two-dimensional axisymmetric domain that represents a slice of the full cylindrical geometry. The model geometry is shown in Figure 2. The explosive is modeled with a single quadrilateral zone (FLAC2D command zone create quadrilateral) of radius and height of 0.1 m. The surrounding rock is modeled with several zones that begin at a radius of 0.1 m and extend an additional 6 m. The explosive (ANFO) and rock properties are given in Tables 1 and 2, respectively.

Figure 2: FLAC2D axisymmetric model geometry, groups, and stress history locations. The model geometry approximates an axisymmetric response around the cylindrical explosive charge. The zones are scaled in the non-radial directions for visualization purposes, i.e., the figure is not to scale.

Energy release within the explosive is controlled by a constant burn fraction set to unity for the model duration, implying instantaneous and complete detonation at time \(t=0\) s. The total model run time is \(t_{max}=1.5L/V_p\) where \(L\) is the the model length in the radial direction and \(V_p\) is the rock P-wave velocity. A factor of 1.5 ensures that the induced stress wave passes through the entire model and is absorbed at the outer boundary by quiet conditions. Stiffness proportional Rayleigh damping is applied to all zones with center frequency of \(10^5\) Hz.

Table 1: Explosive properties (JWL model).

Property	Value	Unit
constant \(A\)	203.582	GPa
constant \(B\)	2.973	GPa
constant \(C\)	0.389	GPa
constant \(R_1\)	6.651
constant \(R_2\)	1.127
constant \(\omega\)	0.390
initial density \(\rho_0\)	800	kg/m3

Table 2: Rock properties (Mohr-Coulomb model).

Property	Value	Unit
density \(\rho\)	2650	kg/m3
bulk modulus \(K\)	23.33	GPa
shear modulus \(G\)	14	GPa
friction angle \(\phi\)	37	degrees
cohesive strength \(c\)	12.5	MPa
tensile strength \(\sigma^t\)	2.5	MPa

Results

Figures 3 and 4 show time histories of pressure and expanded hole radius within the explosive zone. Explosive pressure increases rapidly to 1.6 GPa at the onset of detonation and then decreases as radial expansion occurs. The pressure stabilizes to 150 MPa by the end of the model run time. Furthermore, Figure 5 show the time histories of maximum principal stress (elasticity sign convention, least compressive) at select locations within the rock. The stress histories show large compressive stresses nearby the explosive that quickly attenuate with distance and become tensile at later times. This is consistent with the idealized crushing and fracturing processes shown in Figure 1. Lastly, the model states at the end of the simulation are shown in Figure 6. Shear failure (crushing) occurs nearby the explosive, driven by large increase in compressive stresses. Further away, the rock is failed in tension (fracturing) due to the tensile hoop stresses reaching the tensile strength of the rock. A mixed failure mode is observed in the intermediate region, where both shear and tensile failure occur. The model results are consistent with the expected behavior of explosive-rock interaction.

Figure 3: Pressure within the explosive vs time.

Figure 4: Expanded radius of the explosive vs time. Original hole radius is 0.1 m.

Figure 5: Maximum principal stress (least compressive) histories at select locations.

Figure 6: Model states at the end of the simulation.

Data Files

blast.dat

[r = 0.1]
[L = 200*r]

program call "properties.dat"

zone create quadrilateral point 0 (0,0) ...
                          point 1 (@r,0) ...
                          point 2 (0,@r) ...
                          size 1 1
                    
zone create quadrilateral point 0 (@r,0) ...
                          point 1 ([L+r],0) ...
                          point 2 (@r,@r) ...
                          size [int(L/r)] 1

[gp0 = gp.near((r,0))]
[zp0 = zone.near((0,0))]

zone group "explosive" range position-x -1e12 @r
zone group "rock" range position-x @r 1e12
zone face skin

zone geometry update-interval 1
zone dynamic damping rayleigh 1 1e5 stiff

zone cmodel assign jwl range group "explosive"
zone cmodel assign mohr-coulomb range group "rock"

zone property density @dens a @a b @b c @c r1 @r1 ...
    r2 @r2 omega @omega initial-density @dens ...
    burn-fraction 1.0 range group "explosive"

zone property density @rdens bulk @bulk shear @shear ...
    cohesion @cohesion friction @friction tension @tension ...
    range group "rock"

zone face apply quiet-normal range group "East"
zone face apply quiet-tangential range group "East"
zone gridpoint fix velocity-y 0

history interval 1
model history name "time" dynamic time-total
fish history name "press" [-zone.stress(zp0)->xx]
fish history name "radius" [gp.disp(gp0)->x + r]
zone history name "smax_1" stress-maximum position ([0.10*L+r],0)
zone history name "smax_2" stress-maximum position ([0.25*L+r],0)
zone history name "smax_3" stress-maximum position ([0.50*L+r],0)
zone history name "smax_4" stress-maximum position ([0.75*L+r],0)
zone history name "smax_5" stress-maximum position ([1.00*L+r],0)
zone history name "smin_half_meter" stress-minimum position (0.50, 0)

[global explosive_volume_0 = zone.area(zone.find(1))]
zone mechanical energy active true
model solve-dynamic [tmax]
model save "blast.sav"

properties.dat

fish define set_jwl_params
    global a, b, c, r1, r2, omega, dens
    a = 203.582e9
    b = 2.973e9
    c = 0.389e9
    r1 = 6.651
    r2 = 1.127
    omega = 0.39
    dens = 776
end

fish define set_rock_params
    global rdens, bulk, shear, Vp, tmax
    rdens = 2650
    bulk = 23.33e9
    shear = 14e9
    
    Vp = math.sqrt((bulk+4/3*shear)/rdens)
    tmax = 0.95*L/Vp
    
    global ucs, friction, q, cohesion, tension
    ucs = 50e6
    friction = 37.0
    
    local fric_rad = friction*math.pi/180.0
    q = (1.0+math.sin(fric_rad)) / (1.0-math.sin(fric_rad))
    cohesion = ucs/(2.0*math.sqrt(q))
    tension = 0.1*cohesion
end

[set_jwl_params]
[set_rock_params]

[1]

This example is listed under the present document title in the i Examples dialog (use the menu command Help -> Examples… to access).