FLAC3D Modeling • Problem Solving with FLAC3D

Approach and Project Setup

The modeling of geo-engineering processes involves special considerations, and a design philosophy different from that followed for design with fabricated materials. Analyses and designs for structures and excavations in or on rocks and soils must be achieved with relatively little site-specific data, and an awareness that deformability and strength properties may vary considerably. It is impossible to obtain complete field data at a rock or soil site. For example, information on stresses, properties, and discontinuities can only be partially known, at best.

Since the input data necessary for design predictions are limited, a numerical model in geomechanics should be used primarily to understand the dominant mechanisms affecting the behavior of the system. Once the behavior of the system is understood, it is then appropriate to develop simple calculations for a design process.

This approach is oriented toward geotechnical engineering, in which there is invariably a lack of good data. But in other applications, it may be possible to use FLAC3D directly in design if sufficient data, as well as an understanding of material behavior, are available. The results produced in a FLAC3D analysis will be accurate when the program is supplied with appropriate data.

Modeling on a Spectrum

Modelers should recognize that there is a continuous spectrum of situations, as illustrated below.

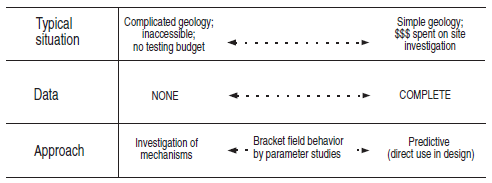
Figure 1: Spectrum of modeling situations.

FLAC3D may be used either in a fully predictive mode (right-hand side of the image above) or as a “numerical laboratory” to test ideas (left-hand side). It is the field situation (and budget), rather than the program, that determines the types of use. If enough data of a high quality are available, FLAC3D can give good predictions.

Since most FLAC3D applications will be for situations in which little data are available, the next topic presents a recommended approach for treating a numerical model as if it were a laboratory test. The model should never be considered to be a “black box” that accepts data input at one end and produces a prediction of behavior at the other. The numerical “sample” must be prepared carefully, and several samples tested, to gain an understanding of the problem.

Recommended Steps

The table below lists the steps recommended to perform a successful numerical experiment; each step is discussed separately below.

Table 1: Recommended Steps for Numerical Analysis in Geomechanics

Step 1	Define the objectives for the model analysis.
Step 2	Create a conceptual picture of the physical system.
Step 3	Construct and run simple idealized models.
Step 4	Assemble problem-specific data.
Step 5	Prepare a series of detailed model runs.
Step 6	Perform the model calculations.
Step 7	Present results for interpretation.

Step 1: Define the Objectives for the Model Analysis

The level of detail to be included in a model often depends on the purpose of the analysis. For example, if the objective is to decide between two conflicting mechanisms that are proposed to explain the behavior of a system, then a crude model may be constructed, provided that it allows the mechanisms to occur. It is tempting to include complexity in a model just because it exists in reality. However, complicating features should be omitted if they are likely to have little influence on the response of the model, or if they are irrelevant to the model’s purpose. Start with a global view and add refinement as (and if) necessary.

Step 2: Create a Conceptual Picture of the Physical System

It is important to have a conceptual picture of the problem to provide an initial estimate of the expected behavior under the imposed conditions. Several questions should be asked when preparing this picture. For example: Is it anticipated that the system could become unstable? Is the predominant mechanical response linear or nonlinear? Are movements expected to be large or small in comparison with the sizes of objects within the problem region? Are there well-defined discontinuities that may affect the behavior, or does the material behave essentially as a continuum? Is there an influence from groundwater interaction? Is the system bounded by physical structures, or do its boundaries extend to infinity? Is there any geometric symmetry in the physical structure of the system?

These considerations will dictate the gross characteristics of the numerical model, such as the design of the model geometry, the types of material models, the boundary conditions, and the initial equilibrium state for the analysis. They will determine whether a three-dimensional model is required, or a two-dimensional model can be used to take advantage of geometric conditions in the physical system.

Step 3: Construct and Run Simple Idealized Models

When idealizing a physical system for numerical analysis, it is more efficient to construct and run simple test models first, before building the detailed model. Simple models should be created at the earliest possible stage in a project, to generate both data and understanding. The results can provide further insight into the conceptual picture of the system; step 2 may need to be repeated after simple models are run.

Simple models can reveal shortcomings that can be remedied before any significant effort is invested in the analysis. For example, do the selected material models sufficiently represent the expected behavior? Are the boundary conditions influencing the model response? The results from the simple models can also help guide the plan for data collection by identifying which parameters have the most influence on the analysis.

Step 4: Assemble Problem-Specific Data

The types of data required for a model analysis include the following:

• details of the geometry (e.g., profile of underground openings, surface topography, dam profile, rock/soil structure);
• locations of geologic structure (e.g., faults, bedding planes, joint sets);
• material behavior (e.g., elastic/plastic properties, post-failure behavior);
• initial conditions (e.g., in-situ state of stress, pore pressures, saturation); and
• external loading (e.g., explosive loading, pressurized cavern).

Because there are typically large uncertainties associated with specific conditions (in particular, state of stress, deformability, and strength properties), a reasonable range of parameters must be selected for the investigation. The results from the simple model runs (in step 3) can often prove helpful in determining this range, and in providing insight for the design of laboratory and field experiments to collect the needed data.

Step 5: Prepare a Series of Detailed Model Runs

Most often, the numerical analysis will involve a series of computer simulations that include the different mechanisms under investigation, and span the range of parameters derived from the assembled database. When preparing a set of model runs for calculation, several aspects, such as the following, should be considered:

1. How much time is required to perform each model calculation? It can be difficult to obtain sufficient information to arrive at a useful conclusion if model runtimes are excessive. Consideration should be given to performing parameter variations on multiple computers to shorten the total computation time.
2. The state of the model should be saved at several intermediate stages so that the entire run does not have to be repeated for each parameter variation. For example, if the analysis involves several loading/unloading stages, the user should be able to return to any stage, change a parameter, and continue the analysis from that stage. The amount of disk space required for save files should be considered.
3. Are there a sufficient number of monitoring locations in the model to provide for a clear interpretation of model results and for comparison with physical data? It is helpful to locate several points in the model at which a record of the change of a parameter (such as displacement, velocity or stress) can be monitored during the calculation. Also, the maximum unbalanced force in the model should always be monitored to check the equilibrium or failure state at each stage of an analysis.

Step 6: Perform the Model Calculations

It is best to first make one or two model runs, split into separate sections, before launching a series of complete runs. The runs should be checked at each stage to ensure that the response is as expected. Once there is assurance that the model is performing correctly, several data files can be linked together to run a complete calculation sequence. At any time during a sequence of runs, it should be possible to interrupt the calculation, view the results, and then continue or modify the model as appropriate.

Step 7: Present Results for Interpretation

The final stage of problem solving is the presentation of the results for a clear interpretation of the analysis. This is best accomplished by displaying the results graphically, either directly on the computer screen or as output to a hard-copy plotting device. The graphical output should be presented in a format that can be directly compared to field measurements and observations. Plots should clearly identify regions of interest from the analysis, such as locations of calculated stress concentrations, or areas of stable movement versus unstable movement in the model. The numeric values of any variable in the model should also be readily available for more detailed interpretation by the modeler.

We recommend that these seven steps be followed to solve geo-engineering problems efficiently. The following sections describe the application of FLAC3D to meet the specific aspects of each of these steps in this modeling approach.

Start a Project

When the initial preparations are complete, the modeling process in FLAC3D starts with the creation of a project. This is a simple but important step. The project “houses” the model and the resources that go into creating it, as well as the outputs that are generated by it.

Create a Project File

To create a new project file, select File --> New Project... from the main menu. This will open a standard dialog that will allow the user to specify the name and folder location of the project file.

Once the file is created, the folder containing the project file will serve as the working directory for the project. All model state (SAV) files will be stored there unless expressly specified by command to be stored elsewhere. In either case, the project will track their existence as part of the project. This allows for a range of facilities, including rapid movement between saved states within the interface, and collection and storage of the commands that comprise each saved state within the State Record pane, which in turn allows for a program undo capability and for creating a bundle file.

The project also saves user interface settings (the layout), model options that have been specified for this project, the state of all program options that are in effect for the project, calculation modes used in the project, and all plots of the model that are created.

The project does not contain saved states, imported files, or data files. These exist as files outside the project. The project does track the use of these files and the locations from which they are drawn.

Project Tools

FLAC3D provides the Project pane for project management. In addition, it provides the Pack facility on the toolbar (Tools ‣ Pack…) for gathering the project file, project source files, and saved state records into a single, easily transmitted/stored file (similar to a compressed archive file). Project files (as part of a bundle) are also the preferred inclusion when sending a technical support request through the Technical Support dialog (Help ‣ Technical Support…).