Finn Model*
Note
*This model is available in FLAC3D only.
In reality, pore pressure build-up is a secondary effect, although many people seem to think it is the primary response to cyclic loading. The primary effect is the irrecoverable volume contraction of the matrix of grains when a material is taken through a complete strain cycle with the confining stress held constant. Since it is grain rearrangement rather than grain volume change that takes place, the volume of the void space decreases under constant confining stress. If the voids are filled with fluid, then the pressure of the fluid increases and the effective stress acting on the grain matrix decreases. Note that pore pressures would not increase if the test were done at constant volume; it is the transfer of externally applied pressure from grains to fluid that accounts for the fluid-pressure increase.
Martin et al. Equation
This mechanism is well-described by Martin et al. (1975), who also note that the relation between irrecoverable volume-strain and cyclic shear-strain amplitude is independent of confining stress. They supply the following empirical equation that relates the increment of volume decrease per cycle of shear strain, \(\Delta\epsilon_{vd}\), to the cyclic shear-strain amplitude, \(\gamma\), where \(\gamma\) is presumed to be the “engineering” shear strain:
where \(C^c_1\), \(C^c_2\), \(C^c_3\), and \(C^c_4\) are constants.
Note
Note that these constants (\(C^c_1\), \(C^c_2\), \(C^c_3\), and \(C^c_4\)) are not identical to model input constants because the input applies to half cycle of shear strain.
Note that the equation involves the accumulated irrecoverable volume strain, \(\epsilon_{vd}\), in such a way that the increment in volume strain decreases as volume strain is accumulated. Presumably, \(\Delta\epsilon_{vd}\) should be zero if \(\gamma\) is zero; this implies that the constants are related as follows: \(C^c_1\ C^c_2\ C^c_4 = C^c_3\). Martin et al. (1975) then go on to compute the change in pore pressure by assuming certain moduli and boundary conditions (which are not clearly defined). We do not need to do this. Provided we correctly account for the irreversible volume change in the constitutive law, FLAC3D will take care of the other effects.
Byrne Equation
An alternative, and simpler, formula is proposed by Byrne (1991):
where \(C^c_1\) and \(C^c_2\) are constants with different interpretations from those of Equation (1). For Equation (2), Byrne (1991) notes that the constant, \(C^c_1\), can be derived from relative densities, \(D_r\), as follows:
Note
Note that these constants (\(C^c_1\) and \(C^c_2\)) are not identical to model input constants because the input applies to half cycle of shear strain.
Further, using an empirical relation between \(D_r\) and normalized standard penetration test values, \({(N_1)_{60}}\),
then
\(C^c_2\) is then calculated from \(C^c_2 = {0.4 / C^c_1}\), in this case. Refer to Byrne (1991) for more details.
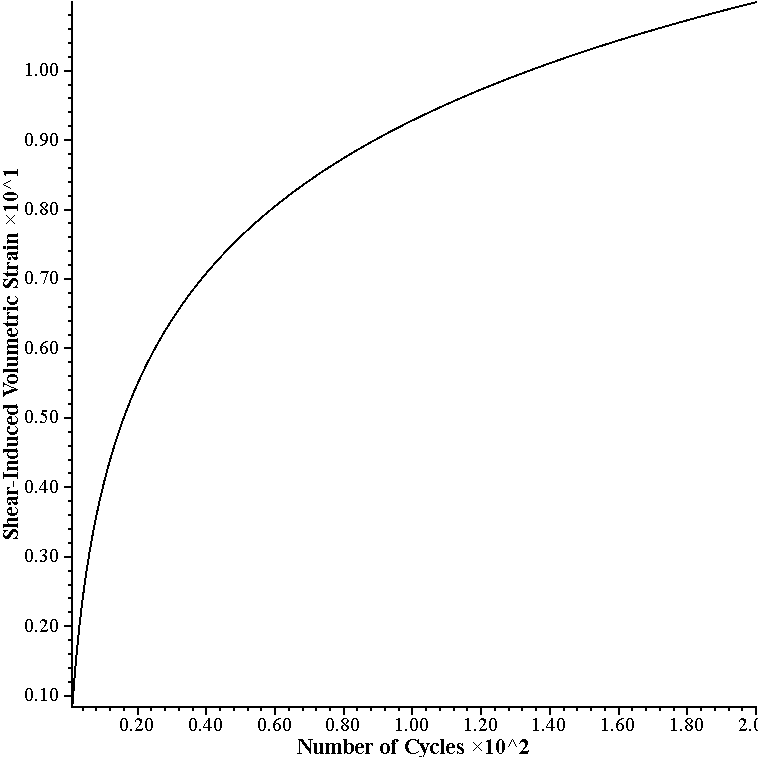
The shear-induced volumetric strain for constant amplitude of cyclic shear strain predicted by this formula is plotted versus number of cycles in Figure 1. The formula predicts an increase in shear-induced (compactive) volumetric strain with the level of cyclic shear-strain. Also, for a given strain amplitude, \(\gamma\), the rate of accumulation decreases with the number of cycles.
The incremental volumetric behavior of the Finn/Byrne model (at the end of a cycle) may be expressed as
where \(\sigma_m = \sigma_{ii} / 3\) is the mean stress, \(p\) is pore pressure, \(\alpha\) is Biot coefficient (= 1 for soil), \(K\) is the drained bulk modulus of the soil and \(\epsilon\) is the volumetric strain. Note that \(\epsilon\) is positive in extension, while \(\epsilon_{vd}\) is positive in compression. For undrained conditions, the change in pore pressure is proportional to the change in volumetric strain:
where \(M\) is Biot modulus. After substitution of Equation (7) into (6), and solving for \(\Delta \epsilon\), we obtain
If the fluid is very stiff compared to the solid matrix (\(M>>>K\)), Equation (8) predicts no change in volume. Further, using \(\Delta \epsilon = 0\) in Equation (9) gives
Equation (9) predicts a decrease in magnitude of effective stress with cyclic shear strain (produced by an increase of shear induced compaction). Under conditions of constant stress, \(\Delta \sigma_m = 0\), there will be an increase in pore pressure that is proportional to the drained bulk modulus of the soil:
While under free stress conditions, the pore pressure will remain unchanged (\(\Delta p = 0\)), and the magnitude of the total stress will decrease according to
Note that in both situations, the drained (tangent) bulk modulus, \(K\), plays an important role in determining the magnitude of the cyclic loading impact on effective stress. The Finn/Byrne model, therefore, captures the main physics of liquefaction.
Finn Model
For a random pattern of strain cycles, it is appropriate to compute volumetric strains per half cycle (\({(\Delta \epsilon_{vd})}_{\rm 1/2 cycle}\)) — see, e.g., Byrne 1991. The Finn built-in constitutive model incorporates the following form of the Martin et al. and Byrne relations into the standard Mohr-Coulomb plasticity model:
Finn Model — Martin et al. Formulation
where \(C_1\), \(C_2\), \(C_3\) and \(C_4\) are model input constants.
Finn Model — Byrne Formulation
In addition to \(C_1\) and \(C_2\), a third model input parameter, \(C_3\), sets the threshold shear strain (i.e., the limiting shear-strain amplitude below which volumetric strain is not produced). The use of Equation (12) or (13) can be selected by setting parameter flag�_switch = 0 or 1, respectively. As it stands, the model captures the basic mechanisms that can lead to liquefaction in sand. In addition to the usual parameters (friction, moduli, etc.), the model needs the four constants for Equation (12), or three constants for Equation (12). For Equation (1), Martin et al. (1975) describe how these may be determined from a drained cyclic test. Alternatively, one may imagine using some trial values to model an undrained test with FLAC3D, and compare the results with a corresponding laboratory test; the constants could then be adjusted to obtain a better match.
Note that following Byrne (1991), the input parameters \(C_1\) and \(C_2\) are related to relative density or blow count as follows:
where \(C^c_1\) is given by Equation (3) or Equation (5), respectively.
In the Finn model, there is logic to detect a strain reversal in the general case. In Martin et al. (1975) (and most other papers on this topic), the notion of a strain reversal is clear, because they consider one-dimensional measures of strain. In a three-dimensional analysis, however, there are at least six components of the strain-rate tensor. The six strain measures are accumulated in the Finn model in FLAC3D as follows:
We use the following scheme to locate extreme points in strain space. Denoting the previous point by superscript (°), and the one before that with (°°), the previous unit vector, \(n_i^\circ\), in strain space is computed:
where subscript \(i\) takes the values 1 to 6, and repeated indices imply summation.
The projection \(d\) of the new vector, \(\epsilon_i - \epsilon_i^{\circ}\), from the old point to the new point is given by the dot product of the new vector with the previous unit vector,
We use the rule that \(d\) must be negative (so that the new strain segment corresponds to a reversal compared to the previous segment). We then monitor the absolute value of \(d\) and make the following calculation when it passes through a maximum, \(d_{\rm max}\), provided that a minimum number of timesteps has elapsed (to prevent the reversal logic being triggered again on transients that immediately follow a reversal). This threshold number of timesteps is controlled by the property named ff�_latency, which is set to 50.0 in the runs reported here.
Having obtained the engineering shear strain, \(\gamma\), we insert it into Equation (12) or (13) and obtain \({(\Delta \epsilon_{vd})}_{\rm 1/2 cycle}\). We then update \(\epsilon_{vd}\), as follows, and save it for use in Equation (12) or (13).
We also save one-third of \({(\Delta \epsilon_{vd})}_{\rm 1/2 cycle}\) and revise the direct strain increments input to the model at the next half cycle:
Note that FLAC3D’s compressive strain increments are negative and \(\Delta \epsilon_{vd}\) is positive. Hence, the mean effective stress decreases.
The logic described above is certainly not perfect, but it seems to work in simple cases. However, the user must verify that the algorithm is appropriate before applying it to real cases. In particular, the number of “half cycles” detected strongly depends on the relative magnitude of horizontal and vertical motion. Hence, the rate of build-up of pore pressure will also be sensitive to this ratio. It may be more practical to consider just the shear components of strain for something like a dam, which is wide compared to its height. Ultimately, we need better experimental data for volume changes during complicated loading paths; the model should then be revised accordingly. One effect that has been shown to be very important (see, for example, Arthur et al. 1980) is the effect of rotation of principal axes: volume compaction may occur even though the magnitude of deviatoric strain (or stress) is kept constant. Such rotations of axes occur frequently in earthquake situations. Another effect that is not incorporated into the Finn model is that of modulus increase induced by compaction—it is known that sand becomes stiffer elastically when compaction occurs by cyclic loading. This modification could be incorporated by using the UDM option.
The Finn model is loaded in FLAC3D with the zone cmodel command
(i.e., zone cmodel assign finn).
The code must be configured for dynamic analysis (model configure dynamic) to apply the model.
As with the other built-in models, the properties are assigned with the zone property command.
The following keywords are used to assign properties for the Finn model:
finn Model Properties
Use the following keywords with the zone property command to set these properties of the Finn model.
- finn
- bulk f
elastic bulk modulus, \(K\)
- cohesion f
cohesion, \(c\)
- constant-1 f
constant, \(C_1\)
- constant-2 f
constant, \(C_2\)
- constant-3 f
constant, \(C_3\)
- constant-4 f
constant, \(C_4\)
- friction f
internal angle of friction, \(\phi\)
- poisson f
Poisson’s ratio, \(\nu\)
- shear f
elastic shear modulus, \(G\)
- young f
Young’s modulus, \(E\)
- flag-brittle b (a)
if true, the tension limit is set to 0 in the event of tensile failure. The default is false.
- table-cohesion s (a)
name of the table relating cohesion to plastic shear strain
- table_dilation s (a)
name of the table relating dilation angle to plastic shear strain
- table-friction s (a)
name of the table relating friction angle to plastic shear strain
- table-tension s (a)
name of the table relating tension limit to plastic tensile strain
- number-count i (r)
number of shear strain reversals (half cycles) detected
- strain-shear-plastic f (r)
accumulated plastic shear strain
- strain-tensile-plastic f (r)
accumulated plastic tensile strain
- strain-volumetric-irrecoverable f (r)
accumulated irrecoverable volume strain, \(\epsilon_{vd}\), which is positive in compression, an interval variable used in Martin et al and Byrne formula
Key
- (a) Advanced property.
- This property has a default value; simpler applications of the model do not need to provide a value for it.
- (r) Read-only property.
- This property cannot be set by the user. Instead, it can be listed, plotted, or accessed through FISH.
Notes
- Only one of the two options is required to define the elasticity: bulk modulus \(K\) and shear modulus \(G\), or Young’s modulus \(E\) and Poisson’s ratio \(\nu\). When choosing the latter, Young’s modulus \(E\) must be assigned in advance of Poisson’s ratio \(\nu\).
- The tension cut-off is \({\sigma}^t = min({\sigma}^t, k_{\phi} / q_{\psi})\).
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |