Transient Fluid Flow to a Well in a Shallow Confined Aquifer
Note
The project file for this example is available to be viewed/run in FLAC3D.[1] The project’s main data files are shown at the end of this example.
A shallow confined aquifer of large horizontal extent is characterized by a uniform initial pore pressure, \(p_0\), and initial isotropic stress, \({\sigma}_{zz}^0\). A well, fully penetrating the aquifer, is producing water at a constant rate, \(q\), per unit depth from time, \(t = t_0\). The elastic porous medium is homogeneous and isotropic, and the flow of groundwater is governed by Darcy’s law. Transient effects are linked to the compressibility of water and the soil matrix. In this problem, the effect of pore-pressure changes are small compared to the overburden, and the vertical stress in the aquifer may be assumed to remain constant with time. Also, horizontal strains are neglected compared to the vertical ones. The conditions of fluid flow to the well are illustrated schematically in Figure 1. The numerical solution to this problem is presented using both coupled and uncoupled modeling approaches.

Figure 1: Flow to a well in a shallow confined aquifer.
A cylindrical system of coordinates is chosen with the \(z\)-axis pointing upward in the direction of the well axis. Substitution of the transport law in the fluid mass-balance equation gives, taking into consideration that \({\epsilon}_{rr} = {\epsilon}_{\theta \theta}\) = 0,
where \(k\) is the homogeneous permeability coefficient, \(M\) is the Biot modulus, and \(\alpha\) is the Biot coefficient.
Partial differentiation, with respect to time, of the elastic constitutive relation \({\sigma}_{zz} - {\sigma}_{zz}^0 + \alpha(p - p_0) = \alpha_1 {\epsilon}_{zz}\) yields, for constant \({\sigma}_{zz}\),
where \(\alpha_1 = K + 4/3 G\).
Using this last equation to express \({\epsilon}_{zz}\) in terms of \(p\) in Equation (1), we obtain, after some manipulations,
where \(c = k/S\) is the diffusion coefficient, \(S = 1/M + {\alpha}^2 / {\alpha_1}\) is the storage coefficient, and, with the problem being axisymmetric and not dependent on \(z\), the Laplacian of \(p\) may be expressed as
The solution to this differential equation with boundary conditions
is due to Theis (1935). It has the form
where \(\hat{p} = p k/q\). The dimensionless variable \(u\) is given by
and \(E_1\) is the exponential integral, defined as
The vertical displacement may be obtained by integration of the equilibrium equation \(\partial {\sigma}_{zz}/\partial z\) = 0 after expressing \(\sigma_{zz}\) in terms of \(\epsilon_{zz}\) by means of the mechanical constitutive equation and substituting \(\partial \epsilon_{zz} / \partial z\) for \(\epsilon_{zz}\). This yields, after substitution of the boundary condition, and using Equation (7),
where \({\hat{u}}_z = u k \alpha_1 /(\alpha q H)\) and \({\hat{x}} = z/H\).
The stresses are derived from the mechanical constitutive equations and Equation (7) for \(\hat{p}\). They have the form
where \(\hat{\sigma} = \sigma k \alpha_1 / (q \alpha G)\).
The FLAC3D grid for this problem corresponds to a nine-degree wedge in a hollow cylinder of unit height. The axis and radius of the well correspond to cylinder axis and radius, respectively. The cylinder outer radius is selected as 100 m to model the far boundary of the flow domain. Figure 2 shows the FLAC3D grid.
A total of 31 zones are used, lined up, and graded in the radial direction. The displacements are fixed in the radial and tangential directions, and in the vertical direction at the cylinder base. A vertical pressure of magnitude \(- \sigma_{zz}^0\) is applied at the top of the model.
The properties for this example are defined:
| dry bulk modulus (\(K\)) | 118 MPa |
| dry shear modulus (\(G\)) | 71 MPa |
| water bulk modulus (\(K_f\)) | 2 GPa |
| Biot coefficient (\(\alpha\)) | 1.0 |
| porosity (\(n\)) | 0.4 |
| permeability (\(k\)) | 2.98 × 10-8 \({m^2}/{Pa-sec}\) |
The initial pore pressure is 147 kPa, and the initial isotropic stress is -147 kPa. Because the Biot coefficient is equal to one (incompressible soil grains), the Biot modulus is equal to the ratio between water bulk modulus and porosity (in this case, \(M\) = 5 GPa). The well-pumping rate per unit aquifer thickness is 2.21 10-3 m2/s, and the well radius, \(r_w\), is selected as 1 m.
Stresses and pore pressures are initialized to the values given above. The well flow-rate is modeled as a surface flux of magnitude \(q/(2 \pi r_w)\) applied to the well radius \(r = r_w\).
The coupled problem is solved (model fluid active on and model mechanical active
on) using the explicit solution algorithm. The maximum out-of-balance mechanical force is
limited to 10.0, the maximum number of mechanical sub-steps in the coupled fluid-mechanical calculation
step is limited to 1000, and the mechanical process is the “slave” module to the master fluid-flow
process. This is accomplished with the commands
model fluid substep 100
model mechanical substep 1000
model mechanical slave on
By specifying these commands, the out-of-balance mechanical force will be kept to a small value while the fluid-flow calculation proceeds.
This example is pore-pressure driven, and the value for the stiffness ratio, \(R_k\), is approximately 23 for the specified fluid bulk modulus of 2 GPa. Thus, the flow calculation may be uncoupled from the mechanical calculation, and the approach discussed in Stiffness Ratio may be applied. The fluid modulus during the flow-only step is defined by Equation (7) in order to preserve the diffusivity of the system. During the mechanical-only step, the fluid modulus is set to zero to prevent further adjustments by volumetric strains. The following commands are applied for the uncoupled calculation for a 4-second flow time:
model fluid active on
model mechanical active off
zone gridpoint initialize fluid-modulus = @uwb
model solve time-total 4.
model fluid active off
model mechanical active on
zone gridpoint initialize fluid-modulus = 0.0
model solve unbalanced-maximum 10.
The FISH variable uwb is the adjusted fluid modulus calculated by Equation (7). Note that, if conditions are such that \(R_k <<< 1\), it is not necessary to adjust the fluid modulus during the flow calculation because the diffusivity will be accurate.
The analytical solutions for pore pressure, stresses, and vertical displacement are programmed as a FISH function. The exponential integral function used in the analytical solutions is programmed as a separate FISH function. Analytical and numerical values are stored in tables. The results are then compared in graphical form. The pore-pressure comparison at selected times is presented in Figure 3 for the coupled solution, and Figure 4 for the uncoupled solution. The vertical displacement values and stresses at 32 seconds are processed by the FISH function well�_32 and are illustrated in Figure 5 and Figure 7 for the coupled solution, and in Figure 6 and Figure 8 for the uncoupled solution.
The results for both the coupled and uncoupled solutions are essentially identical and compare well with the analytical solution. The uncoupled solution is reached much more quickly than the coupled solution. Note that the coupled calculation requires more than 500,000 steps, while the uncoupled calculation requires approximately 16,000 steps.
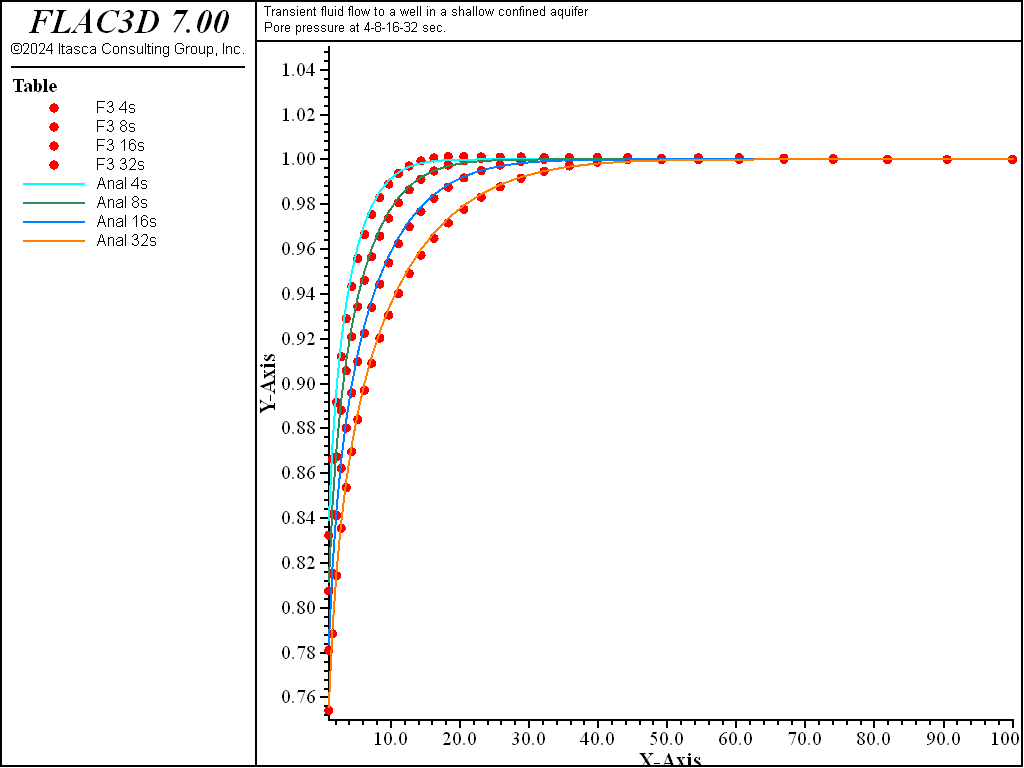
Figure 3: Pore-pressure distribution at 4, 8, 16, and 32 seconds—coupled solution (analytical values = lines; numerical values = symbols).
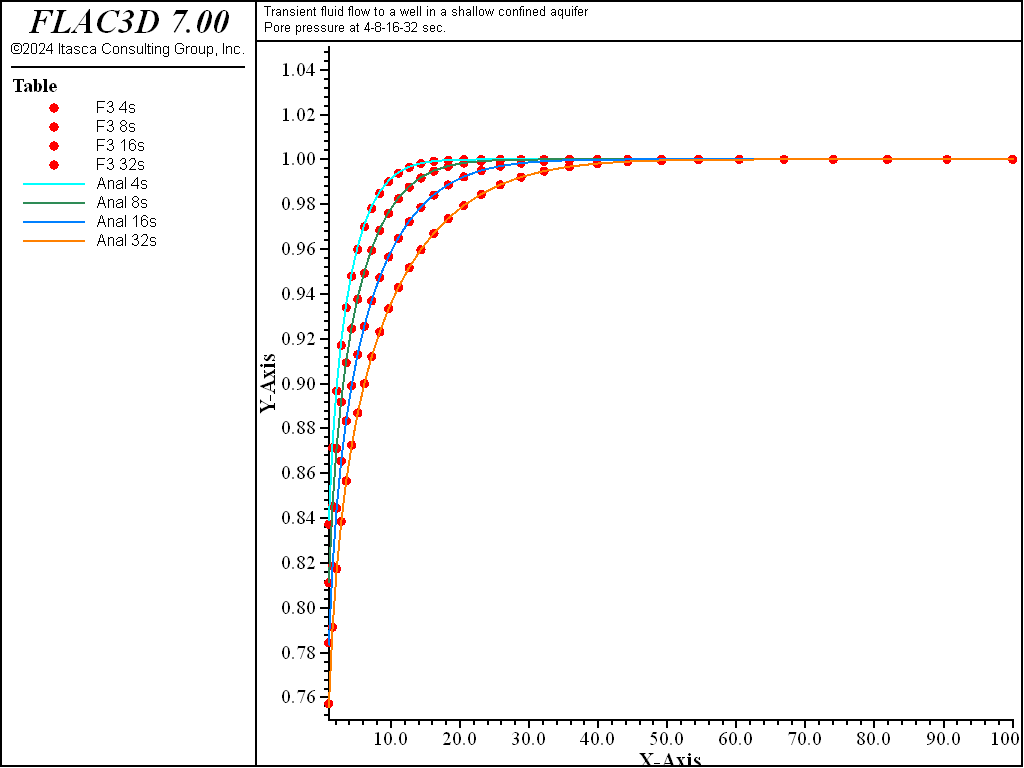
Figure 4: Pore-pressure distribution at 4, 8, 16, and 32 seconds—uncoupled solution (analytical values = lines; numerical values = symbols).
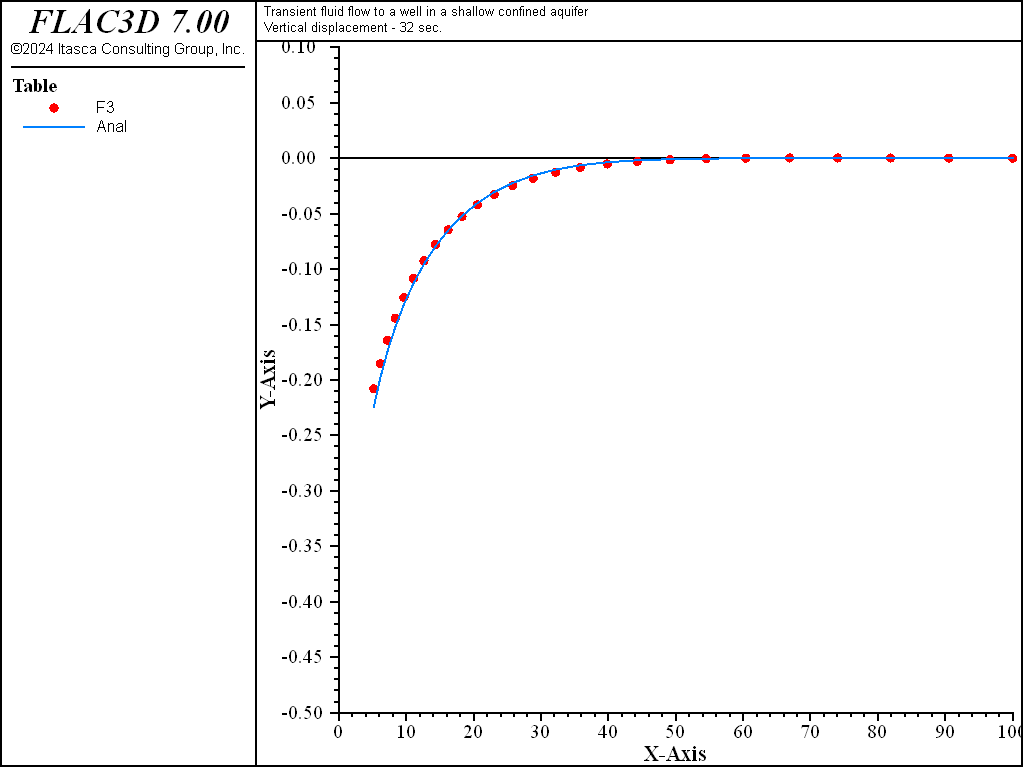
Figure 5: Radial, tangential, and vertical stress distributions at 32 seconds — coupled solution (analytical values = lines; numerical values = symbols).
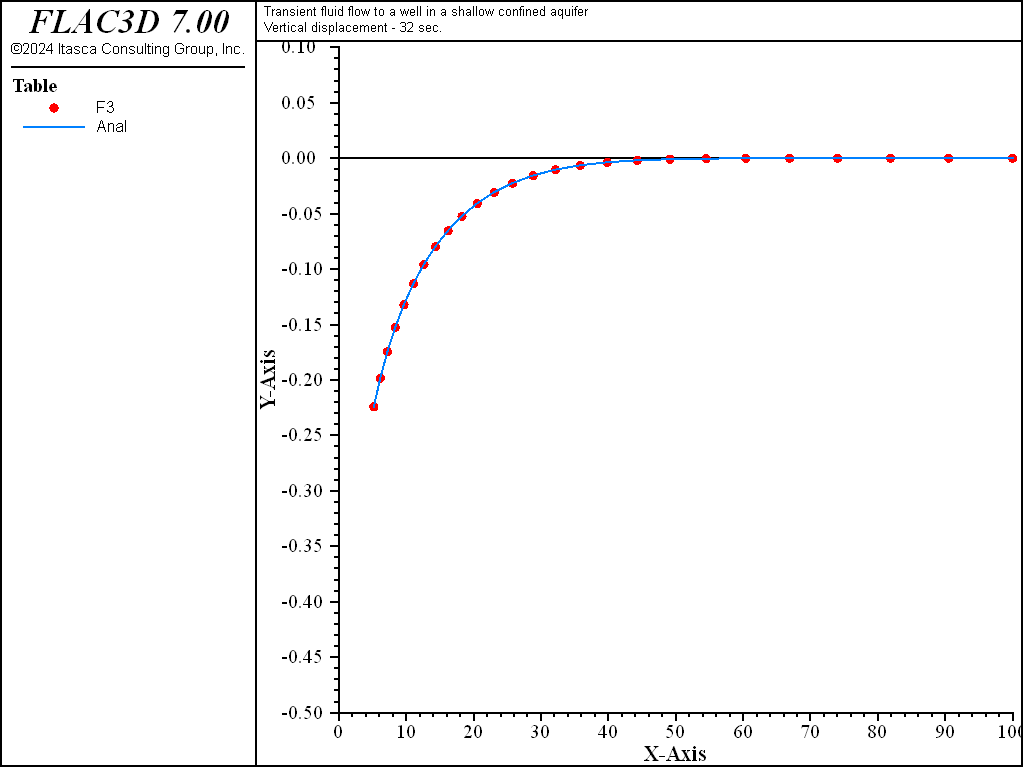
Figure 6: Radial, tangential, and vertical stress distributions at 32 seconds — uncoupled solution (analytical values = lines; numerical values = symbols).
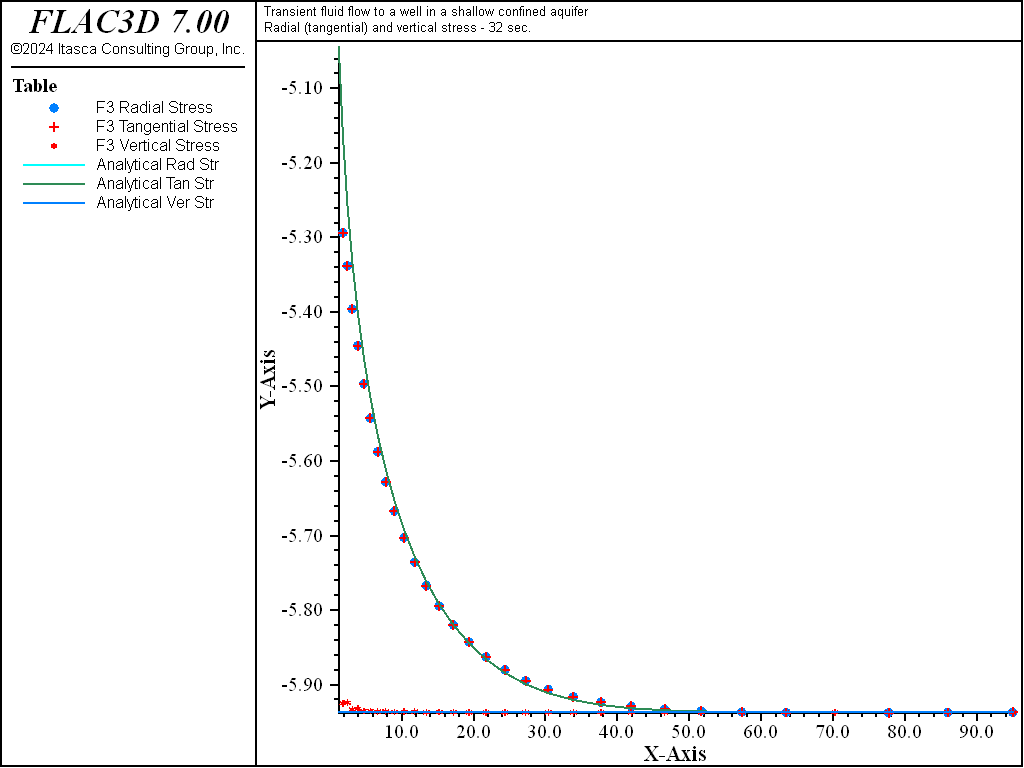
Figure 7: Radial displacement distribution at 32 seconds—coupled solution (analytical values = line; numerical values = symbols).
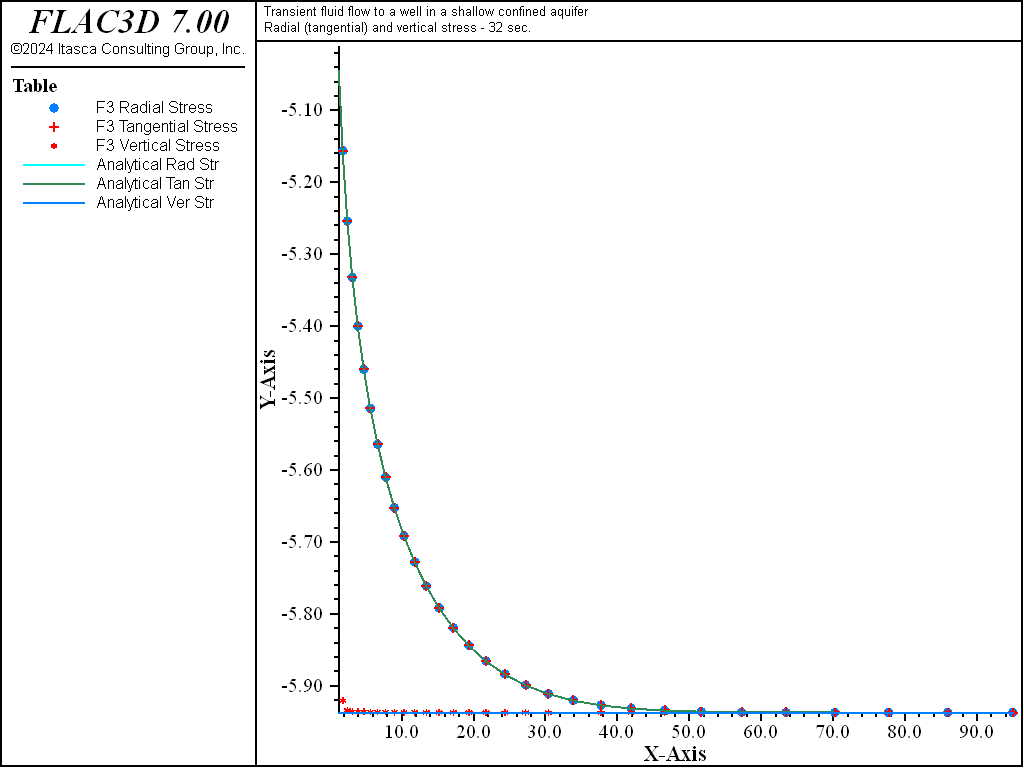
Figure 8: Radial displacement distribution at 32 seconds—uncoupled solution (analytical values = line; numerical values = symbols).
Reference
Theis, C. V. “The Relation between the Lowering of the Piezometric Surface and the Rate and Duration of Discharge of a Well Using Groundwater Storage,” Trans. Am. Geophys. Union, 10, 519-524 (1935).
Data File
WellConfinedAquifer.dat
model new
model title 'Transient fluid flow to a well in a shallow confined aquifer'
fish automatic-create off
model configure fluid
; --- model geometry (hollow cylinder - 9 degree wedge) ---
zone create brick point 0 (1,0,0) point 1 (100,0,0) ...
point 2 (0.987688,0.156434,0) point 3 (1,0,1) ...
point 4 (98.7688,15.6434,0) point 5 (0.987688,0.156434,1) ...
point 6 (100,0,1) point 7 (98.7688,15.6434,1) ...
size (31,1,1) ratio (1.1,1,1)
zone face skin
zone gridpoint group 'xline1' range position (1,0,0) (100,0,0)
zone gridpoint group 'xline2' range position (5,0,1) (100,0,1)
; --- mechanical model ---
zone cmodel assign elastic
zone property bulk 11.8e7 shear 7.1e7
zone face apply velocity-x 0
zone face apply velocity-y 0
zone face apply velocity-z 0 range group 'Bottom'
zone initialize stress xx -1.47e5 yy -1.47e5 zz -1.47e5
zone face apply stress-zz -1.47e5 range group 'Top'
; --- fluid flow model ---
zone fluid cmodel assign isotropic
zone fluid property permeability 2.98e-8 porosity 0.4
zone gridpoint initialize fluid-modulus 2e9
zone gridpoint initialize pore-pressure 147000
; [] = Equivalent flux
zone face apply discharge [-2.21e-3/(2*math.pi)] range group 'West'
; --- setting ---
model large-strain off
model fluid active on
model save 'well-ini'
; --- pumping (coupled analysis) ---
model fluid substep 100
model mechanical substep 1000
model mechanical slave on
model solve fluid time-total 4 mechanical convergence 1
model save 'well-cpl4'
model solve fluid time-total 8 mechanical convergence 1
model save 'well-cpl8'
model solve fluid time-total 16 mechanical convergence 1
model save 'well-cpl16'
model solve fluid time-total 32 mechanical convergence 1
model save 'well-cpl32'
; --- pumping (uncoupled analysis) ---
model restore 'well-ini'
[global fmod = 0.4 / ((0.4/2e9)+(1.0/(11.8e7 + (4/3)*7.1e7)))]
; Adjusted fluid modulus
model fluid active on
model mechanical active off
zone gridpoint initialize fluid-modulus = [fmod]
model solve fluid time-total 4
model fluid active off
model mechanical active on
zone gridpoint initialize fluid-modulus = 0
model solve convergence 1
model save 'well-ucpl4'
model fluid active on
model mechanical active off
zone gridpoint initialize fluid-modulus = [fmod]
model solve fluid time-total 8
model fluid active off
model mechanical active on
zone gridpoint initialize fluid-modulus = 0
model solve convergence 1
model save 'well-ucpl8'
model fluid active on
model mechanical active off
zone gridpoint initialize fluid-modulus = [fmod]
model solve fluid time-total 16
model fluid active off
model mechanical active on
zone gridpoint initialize fluid-modulus = 0
model solve convergence 1
model save 'well-ucpl16'
model fluid active on
model mechanical active off
zone gridpoint initialize fluid-modulus = [fmod]
model solve fluid time-total 32
model fluid active off
model mechanical active on
zone gridpoint initialize fluid-modulus = 0
model solve convergence 1
model save 'well-ucpl32'
Endnotes
| [1] | To view this project in FLAC3D, use the program menu.
⮡ FLAC |
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |

