Power Model: Cylindrical Cavity

Note

To view this project in 3DEC, use the menu command Help ► Examples…. The project’s main data files are shown at the end of this example.

The power-law creep model in 3DEC is used to solve the problem of radial creep of an infinitely long, thick-walled cylinder. A comparison is made with an analytical solution.

The cylinder is subject to a pressure on the outer surface. The creep behavior of the material is defined by a single-component power law:

\[\dot \epsilon_{cr} = A \bar \sigma^n\]

For this problem, \(A\) = 1 × 10^-7 MPa^-3 yr^-1 (or 1 × 10^-25 Pa^-3 yr^-1), and \(n\) = 3. The elastic properties of the material are \(E\) = 820 MPa and \(\nu\) = 0.3636.

An analytical steady-state solution to this problem has been provided by van Sambeek (1986) and is reproduced here:

\[\begin{split}\begin{split} \sigma_r &= - P_b + P_b\ \biggl[ {{(b/r)^{2/n} - 1} \over {\ (b/a)^{2/n}} - 1} \biggr] \\ \sigma_\theta &= - P_b - P_b \biggl[ {{[(2-n)/n]\ (b/r)^{2/n} + 1} \over {(b/a)^{2/n}} - 1} \biggr] \\ \sigma_z &= - P_b - P_b \biggl[ {{[(1-n)/n]\ (b/r)^{2/n} + 1} \over {(b/a)^{2/n}} - 1} \biggr] \\ \dot u_r &= - A\ {(3/4)^{(n+1)/2}} \ {\biggl[ P_b\ {{2/n} \over {(b/a)^{2/n} - 1}} \biggr]}^n {b^2/r} \end{split}\end{split}\]

where: \(\sigma_r\), \(\sigma_\theta\), are radial and tangential stress components;

\(\sigma_z\)	is the out-of-plane stress component;
\(P_b\)	is the applied boundary stress;
\(\dot u_r\)	is the radial displacement rate;
\(a\), \(b\)	are the inner and outer radii of the cylinder, respectively; and
\(r\)	is the radius to point of calculation.

Figure 1 shows the 3DEC grid. Taking advantage of symmetry, only a quarter is represented. A single layer of blocks is used in the out-of-plane direction. The inner radius is \(a\) = 1 and the outer radius is \(b\) = 20.

Gridpoints were fixed in the out-of-plane direction and in the circumferential direction. A pressure of 100 MPa was applied at the outer boundary.

The initial stresses, corresponding to an elastic cylinder in plane strain without a hole, were

\[\sigma_{xx} = \sigma_{yy} = \sigma_{zz} = -P_b = -100 {\hbox{ MPa}}\]

The cylinder was allowed to come to elastic equilibrium by setting creep to off. Then, the creep timestep was set to its initial value (defined by model creep timestep minimum) and allowed to increase automatically until steady state was reached. The maximum allowable timestep (defined by model creep timestep maximum) was determined by the procedure described in Solving Creep Problems.

Figure 1: 3DEC grid for cylindrical cavity test.

The data file for this problem is given at the end of this section. The analytical solution is included in the project as a FISH function powcyl.

The results of this example are summarized in Figure 2 through Figure 5. Figure 2 compares the analytical solution for the radial velocity in the steady-state condition with the 3DEC results. Figure 3 shows the comparison of radial and hoop stresses. Figure 4 shows the history of the radial velocity at the cavity. Some oscillation occurs initially, but the steady-state solution is quickly reached. The initial high value is to be expected since the pre-creep state is far from equilibrium. The final value is within 2.5% of the analytical solution. Figure 5 shows the evolution of the timestep from its initial value of 10^-4 to the maximum value of 1.

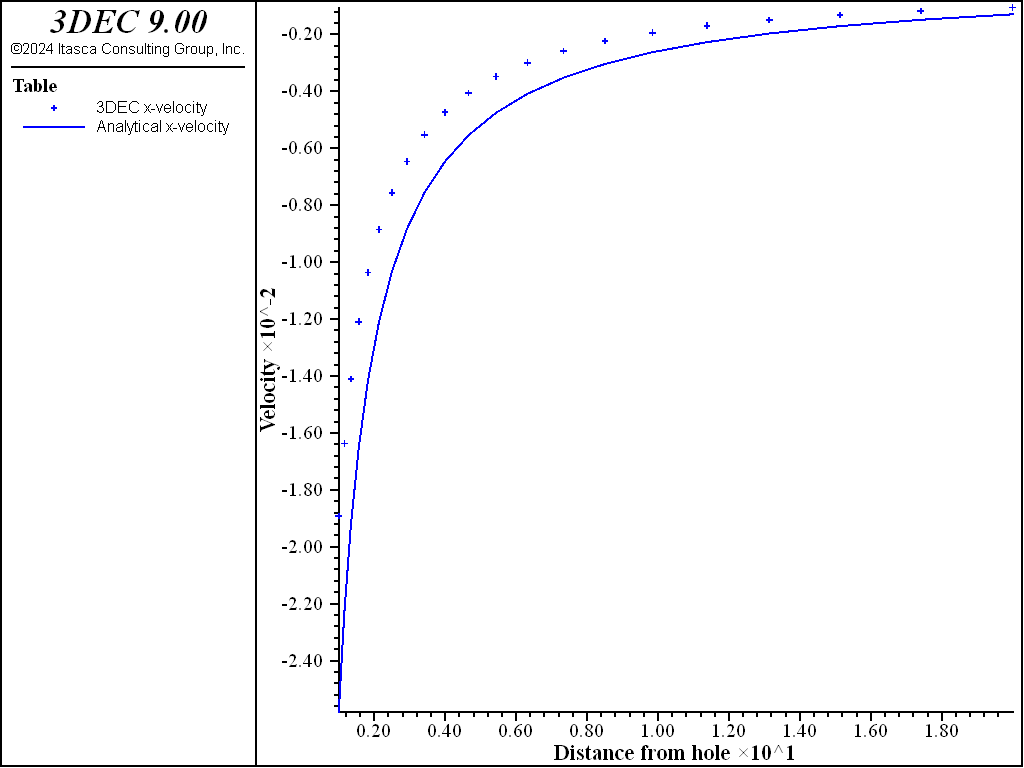
Figure 2: Comparison of radial velocity at steady state—3DEC versus analytical.

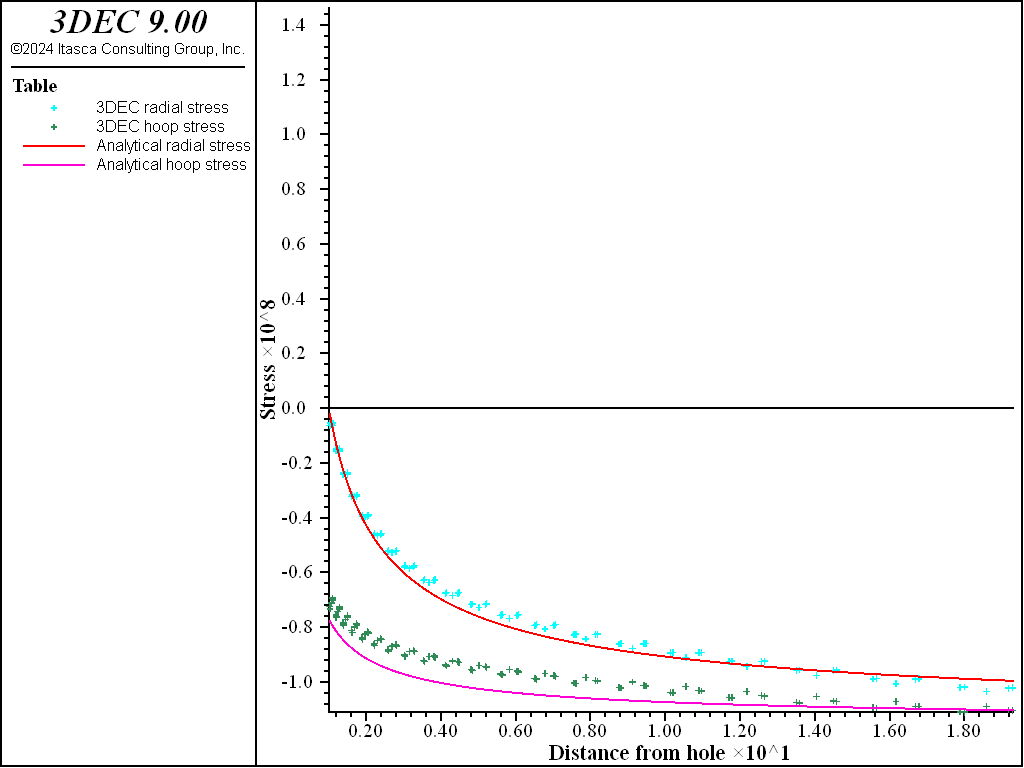
Figure 3: Comparison of radial and hoop stress at steady state—3DEC radial stress versus analytical radial stress and 3DEC hoop stress versus analytical hoop stress.

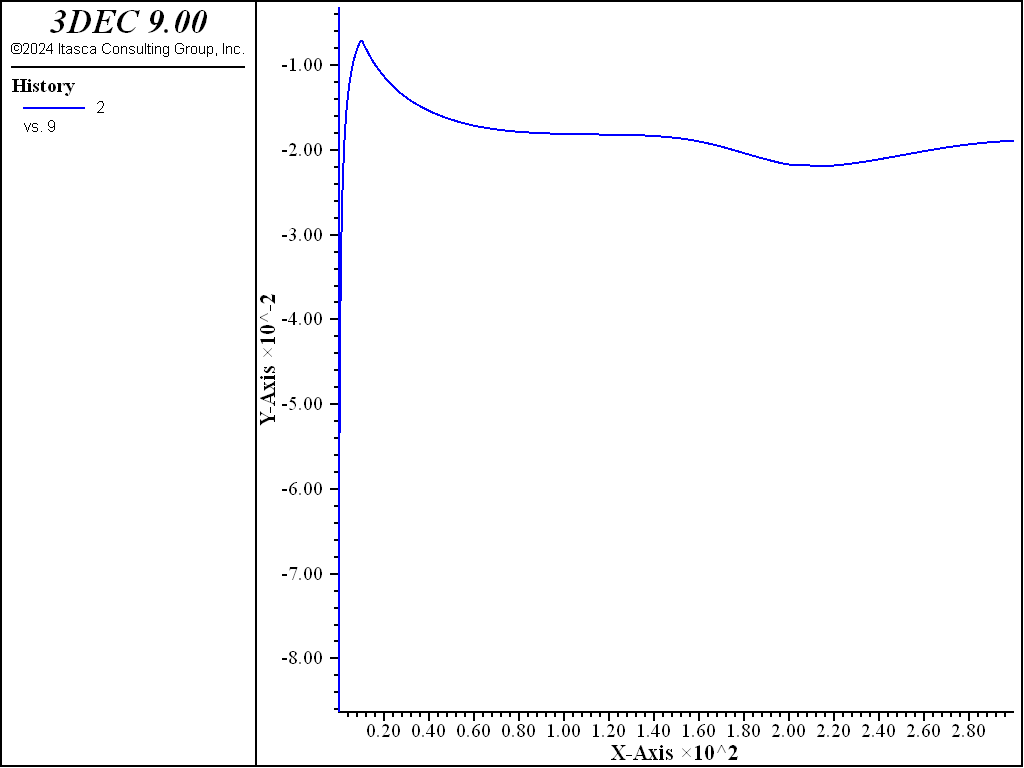
Figure 4: History of radial velocity at the cylindrical cavity.

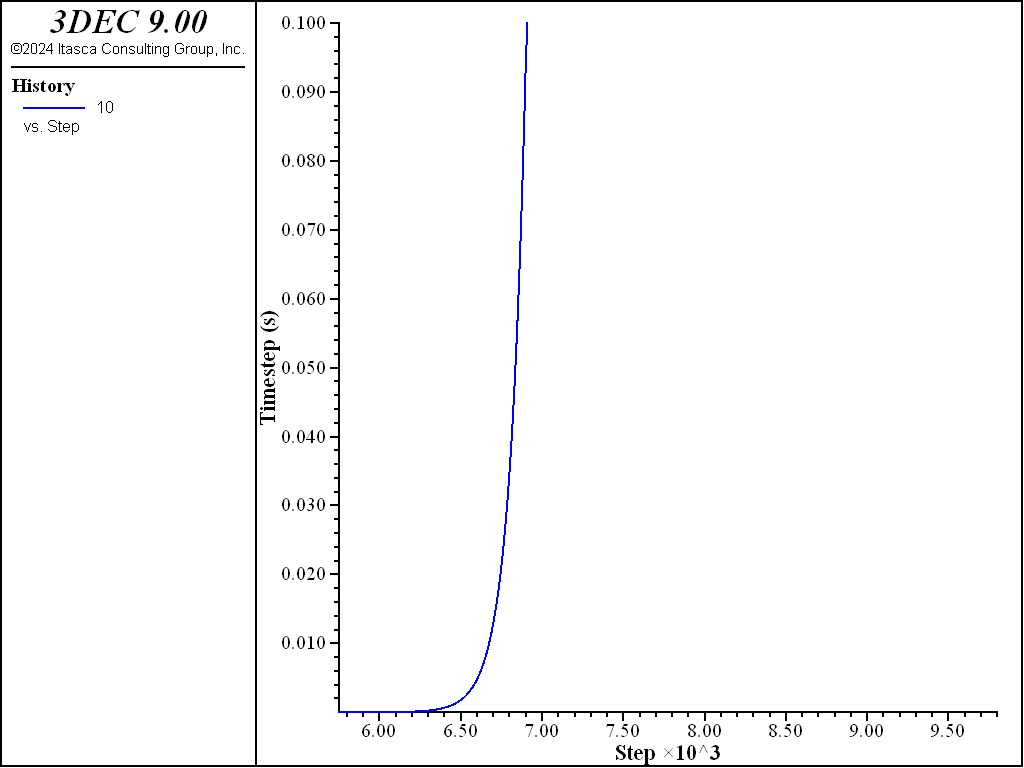
Figure 5: History of timestep for cylindrical cavity test.

Data File

CylindricalCavityPower.dat

;------------------------------------------------------------
;       cylindrical cavity -- power law model
;-------------------------------------------------------------------
model new
fish automatic-create off
model title "Power-Law Creep Model --- Cylindrical Cavity"

model configure creep
model large-strain off

block tolerance 0.001
;
program call 'cylinder.fis'
[r_inner = 1.0]
[r_outer = 20.0]
[nr = 20] 
[nd = 1]
[nc = 10]
[ratio = 1.1]
[length = 0.1]
[cylinder]

block join on

;block zone generate center 0 0 0 edgelength-center 0.1 edgelength-dist 2.5 distance 20
block zone generate hexahedra

block zone cmodel power
; Properties and stresses in Pascal units (not MPa)
block zone property density 2500 bulk=1e9 shear=3e8 constant-1=1e-25 exponent-1=3

;block zone cmodel el
;block zone property density 2500 bulk=1e9 shear=3e8
;
; apply stress first!
block face apply stress -100e6 -100e6 -100e6 0 0 0 ...
  range cylinder end-1 0 0 0 end-2 0 0 -1 radius 19 21

block gridpoint apply velocity-x 0 range position-x 0
block gridpoint apply velocity-y 0 range position-y 0
block gridpoint apply velocity-z 0 range position-z -1 0

block zone initialize stress xx -100e6 yy -100e6 zz -100e6
;
model creep active off
model solve ratio 1e-7

model save 'cyl_1'

model history mechanical unbalanced-maximum
block history velocity-x position 1 0 0
block history velocity-x position 20 0 0
block history displacement-x position 1 0 0
block history displacement-x position 20 0 0
block history stress-xx position 1 0 0
block history stress-yy position 1 0 0
block history stress-zz position 1 0 0
model history creep time-total
model history timestep
;
block gridpoint initialize velocity (0,0,0)
model creep active on
model creep timestep starting 1.0e-6
model creep timestep minimum 1.0e-6
model creep timestep maximum 0.1

model solve time-total 300
model save 'cyl_2'

; compare analytic solution......
program call 'solution.fis' suppress 
table  '1' label '3DEC x-velocity'
table '11' label 'Analytical x-velocity'
table  '2' label '3DEC radial stress'
table '12' label 'Analytical radial stress'
table  '3' label '3DEC hoop stress'
table '13' label 'Analytical hoop stress'
table  '4' label '3DEC out-of-plane stress'
table '14' label 'Analytical out-of-plane stress'
model save 'cylindrical-cavity-power'
program return