Sliding Wedge
Problem Statement
Note
The project file for this example may be viewed/run in 3DEC.[1] The main data files used are shown at the end of this example.
Stability of a wedge in a rock mass, formed by two intersecting planar surfaces under the action of gravity, is analyzed using 3DEC. The wedge is formed by two structural features defined by:
A: dip = 40° dip direction = 130°
B: dip = 60° dip direction = 220°
The same mechanical properties are assumed for both planes.
Analytical Solution
A classical wedge stability analysis is presented in Hoek and Bray (1977). For the case of cohesionless joints with an equal friction angle, the safety factor, \(F\), of the wedge is independent of its size and can be calculated from the formula
where \(R_A\) is the reaction force normal to plane A, \(R_B\) is the reaction force normal to plane B, \(\phi\) is the friction angle of the joints, \(W\) is the weight of the wedge, and \(\psi\) is the inclination of the intersection line (between joints A and B) relative to the horizontal. It is possible to calculate a critical friction angle (for which the wedge is at limit equilibrium) for the given wedge from the equation above. The solution is implemented using the FISH function _safety (see data file “SAFETY.FIS”), and the results are compared to 3DEC calculations.
3DEC Model
The 3DEC model shown in Figure 1 consists of four rigid blocks. Three of the blocks are fixed, and only the isolated wedge is allowed to move under gravity. The mechanical properties selected for this model are:
density: \(\rho\) = 2000 kg/m3
joint shear and normal stiffness: \(K_n\) = \(K_s\) = 10 MPa/m
gravity acceleration: \(g\) = 10 m/sec2
Two of the wedge faces have contact with faces of adjacent blocks. The edge at the back of the wedge has contact with an intersection of two rear blocks. Joint shear and normal stiffnesses of 10 MPa/m are assigned to all three contacts. The wedge is first allowed to consolidate under its weight by setting the friction on both planes to a high value and applying adaptive global damping. Then, friction is reduced until failure occurs. A history of vertical velocity of the wedge (shown in Figure 2) clearly indicates the simulation step at which instability occurs. Figure 1 shows the failure mechanism in progress. The data file used for the simulation is presented in data file “WEDGE.DAT”.
Results and Discussion
Note that the problem is statically determinate and size-independent. Therefore, the joint stiffness and density do not affect the solution (i.e., critical friction angle). Using 3DEC, a critical friction angle of \(\phi\) = 33.12° is calculated and compared with the analytical solution \(\phi\) = 33.36°. The error of the numerical solution is only 0.7%.
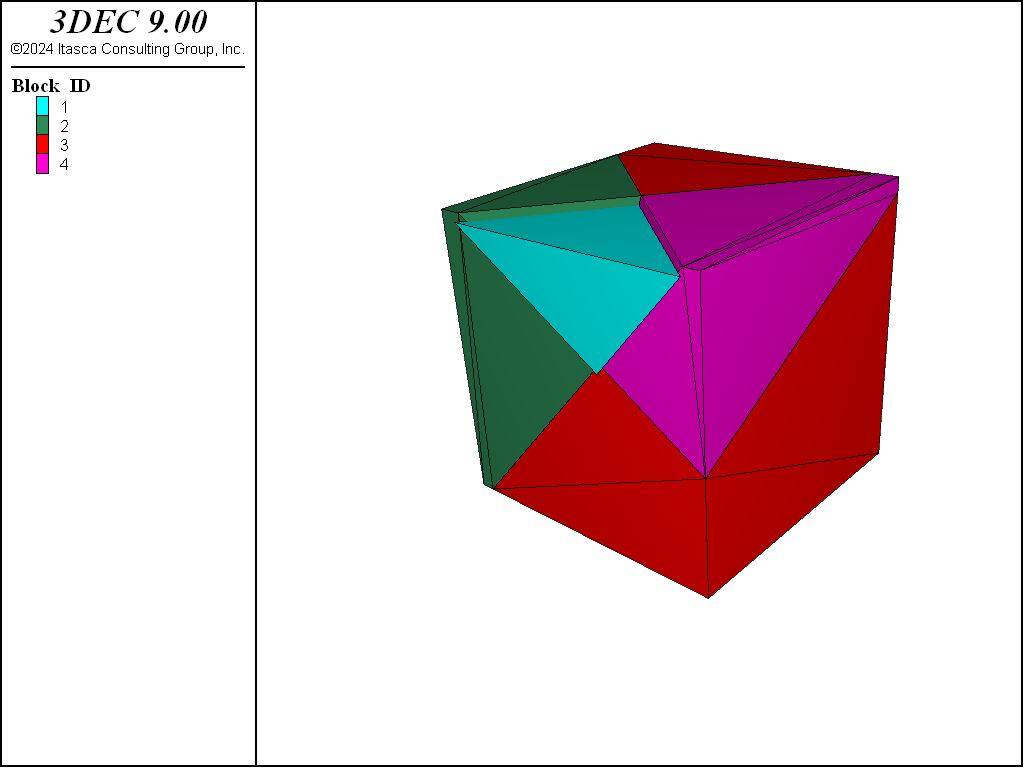
Figure 1: Sliding wedge model.
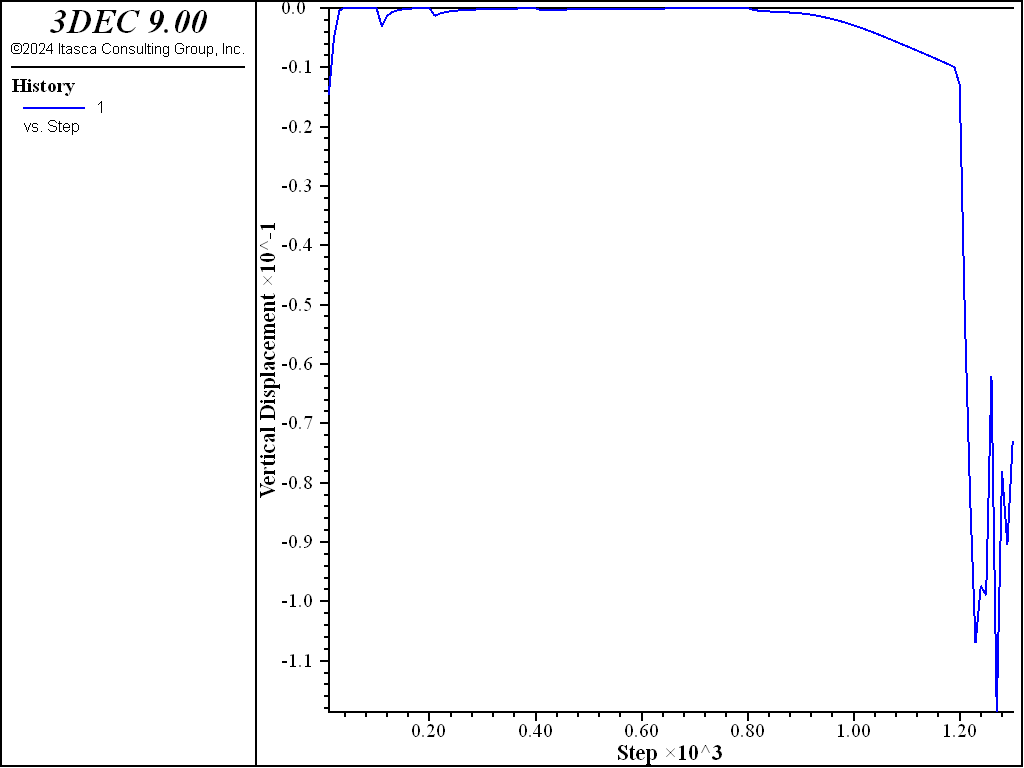
Figure 2: History of vertical velocity of the wedge.
Reference
Hoek, E., and J.W. Bray. Rock Slope Engineering, 2nd Ed. London: Inst. of Mining & Metallurgy (1977).
Data Files
wedge.dat
;===================================================
; verification test -- sliding wedge
; zero cohesion on the joints, equal friction angle
;===================================================
model new
model random 10000
model large-strain on
fish define params
global dip1_ = 40
global dd1_ = 130
global dip2_ = 60
global dd2_ = 220
end
[params]
program call 'safety.fis'
[safety]
block create brick -1 1 -1 1 -1 1
; create two intersecting joints
block cut joint-set dip-direction [dd1_] dip [dip1_] origin 0 0 1
block cut joint-set dip-direction [dd2_] dip [dip2_] origin 0 -0.25 1
; generate subcontacts
block contact generate-subcontacts
; properties
block property density 2e-3
block contact property stiffness-normal 10 stiffness-shear 10 friction 89
block contact material-table default property stiffness-normal 10 ...
stiffness-shear 10
; fix other 3 blocks and apply gravity
block fix range position-z -1 0.8
model gravity 0 0 -10
block mechanical damping global
block hide range position-z -1 0.8
block history velocity-z position .25 -1 .2935
block hide off
; consolidation under gravity with high friction
history name '1' label 'Z Velocity'
model cycle 100
; reduce friction to 35 : stable
block contact property friction 35.00
model cycle 100
; reduce friction to 33.34 : stable
block contact property friction 33.34
model cycle 200
; reduce friction to 33.18 : stable
block contact property friction 33.18
model cycle 400
model save 'wedge_stable'
; reduce friction to 33.12 : failure
block contact property friction 33.12
model cycle 500
model save 'wedge_unstable'
[fric3_ = 33.12]
fish define error_
error_ = (fric_-fric3_)/fric_
end
fish list [error_]
program return
safety.fis
fish define safety
local d3_ = math.sin(dip1_*math.degrad)
local d1_ = -math.cos(dip1_*math.degrad)*math.sin(dd1_*math.degrad)
local d2_ = -math.cos(dip1_*math.degrad)*math.cos(dd1_*math.degrad)
local s1_ = math.sin((dd1_+90.)*math.degrad)
local s2_ = math.cos((dd1_+90.)*math.degrad)
local s3_ = 0.
;
; --- normal to the plane A
;
local n11_ = d2_*s3_-d3_*s2_
local n12_ = d3_*s1_-d1_*s3_
local n13_ = d1_*s2_-d2_*s1_
d3_ = math.sin(dip2_*math.degrad)
d1_ = -math.cos(dip2_*math.degrad)*math.sin(dd2_*math.degrad)
d2_ = -math.cos(dip2_*math.degrad)*math.cos(dd2_*math.degrad)
s1_ = math.sin((dd2_+90.)*math.degrad)
s2_ = math.cos((dd2_+90.)*math.degrad)
s3_ = 0.
;
; --- normal to the plane B
;
local n21_ = d2_*s3_-d3_*s2_
local n22_ = d3_*s1_-d1_*s3_
local n23_ = d1_*s2_-d2_*s1_
;
; --- direction of intersection line
;
local in1_ = 1.0
local in2_ = (-n11_*n23_+n21_*n13_)/(n12_*n23_-n22_*n13_)
local in3_ = (-n21_*n12_+n22_*n11_)/(n12_*n23_-n22_*n13_)
local mag_ = math.sqrt(in1_*in1_+in2_*in2_+in3_*in3_)
in1_ = in1_/mag_
in2_ = in2_/mag_
in3_ = in3_/mag_
;
; --- component of the weight along the intersection line
;
local f11_ = in1_*in3_
local f12_ = in2_*in3_
local f13_ = in3_*in3_
;
; --- component of the weight normal to the intersection line
;
local f21_ = -f11_
local f22_ = -f12_
local f23_ = 1. - f13_
;
; --- normal reactions on planes A and B
;
local r1_ = (f21_*n22_-f22_*n21_)/(n11_*n22_-n21_*n12_)
local r2_ = (f22_*n11_-f21_*n12_)/(n11_*n22_-n21_*n12_)
;
; --- friction coefficient
;
local coef_ = math.abs(in3_)/(math.abs(r1_)+math.abs(r2_))
fric_ = math.atan(coef_)/math.degrad
end
;
Endnote
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Nov 12, 2025 |
