FLAC3D Theory and Background • Constitutive Models

Drucker-Prager Model

The failure envelope for this model involves a Drucker-Prager criterion with tension cutoff. The position of a stress point on this envelope is controlled by a nonassociated flow rule for shear failure, and an associated rule for tension failure.

Formulations

The generalized stress vector \([\underline \sigma]\) involved in the definition of the Drucker-Prager model has two components (\(n\) = 2): the tangential stress, \(\tau\), and mean normal stress, \(\sigma\), defined as

(1)\[ \tau = \sqrt{{{1}\over{2}}\ s_{ij} s_{ij}}\]

(2)\[ \sigma = {{{\sigma}_{kk}}\over{3}}\]

where the Einstein summation convention applies, and \([s]\) is the deviatoric-stress tensor. The components of the associated generalized strain increment vector \(\Delta [\underline\epsilon]\) are the shear-strain increment, \(\Delta \gamma\), and volumetric-strain increment, \(\Delta \epsilon\), introduced as

(3)\[ \Delta \gamma = \sqrt{2 \Delta e_{ij} \Delta e_{ij}}\]

(4)\[ \Delta \epsilon = \Delta {\epsilon}_{kk}\]

where \(\Delta [e]\) is the incremental deviatoric-strain tensor.

Incremental Elastic Law

The incremental expression of Hooke’s law, in terms of the generalized stress and stress increments, has the form

(5)\[ \Delta \tau = G \Delta {\gamma}^e\]

(6)\[ \Delta \sigma = K \Delta {\epsilon}^e\]

where \(K\) and \(G\) are the bulk and shear modulus, respectively.

For future reference, comparing those expressions on \(S_i\) in Incremental Formula:

(7)\[ S_1 (\Delta {\gamma}^e, \Delta {\epsilon}^e) = G \Delta {\gamma}^e\]

(8)\[ S_2 (\Delta {\gamma}^e, \Delta {\epsilon}^e) = K \Delta {\epsilon}^e\]

Composite Failure Criterion and Flow Rule

The failure criterion used for this model is a composite Drucker-Prager criterion with tension cutoff as sketched in the \((\tau, \sigma)\) representation of Figure 1. The failure envelope \(f(\tau, \sigma)\) = 0 is defined, from point \(A\) to \(B\) on the figure, by the Drucker-Prager failure criterion \(f^s\) = 0, with

(9)\[ f^s = \tau + q_{\phi}\ \sigma - k_{\phi}\]

and, from \(B\) to \(C\), by the tension failure criterion \(f^t\) = 0, with

(10)\[ f^t = \sigma - {\sigma}^t\]

where \(q_{\phi}\), \(k_{\phi}\), and \({\sigma}^t\) are positive material constants, and \({\sigma}^t\) is the tensile strength for the Drucker-Prager model. Note that, for a material whose property \(q_{\phi}\) is not equal to zero, the maximum value of the tensile strength is given by

(11)\[ {\sigma}_{max}^t = {{k_{\phi}}\over{q_{\phi}}}\]

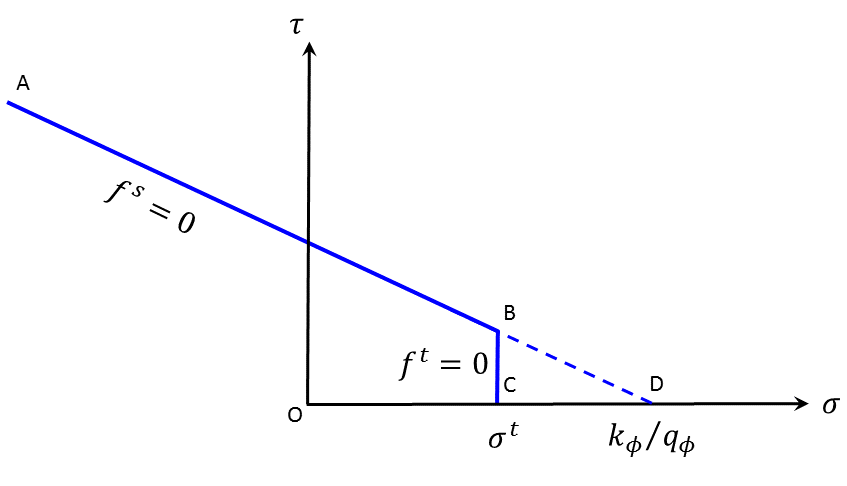
Figure 1: FLAC3D Drucker-Prager failure criterion.

The potential function \(g(\tau, \sigma) = constant\) is composed of two functions, \(g^s\) and \(g^t\), used to describe shear and tensile plastic flow, respectively. The function \(g^s\) corresponds in general to a nonassociated law, and has the form

(12)\[ g^s = \tau + q_{\psi}\ \sigma\]

where \(q_{\psi}\) is a constant, equal to \(q_{\phi}\) if the flow rule is associated. The function \(g^t\) corresponds to an associated flow rule, and is given by

(13)\[ g^t = \sigma\]

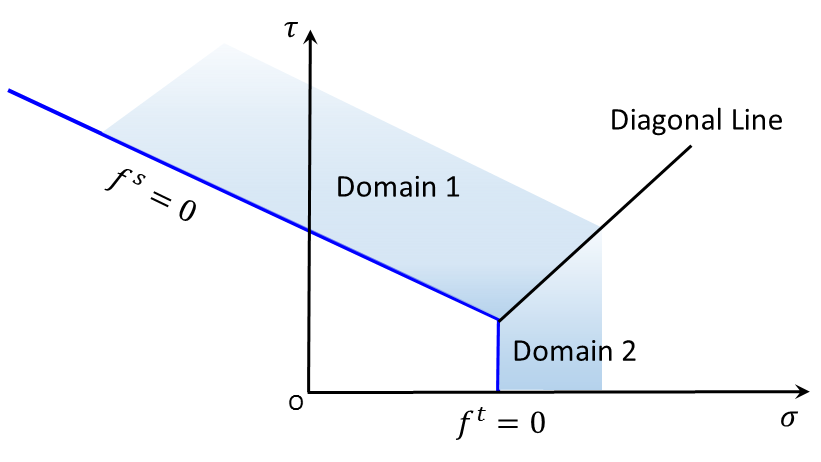
Figure 2: Drucker-Prager model—domains used in the definition of the flow rule.

The flow rule is given a unique definition by application of the following technique. The diagonal line between the representation of \(f^s\) = 0 and \(f^t\) = 0 in the \((\tau, \sigma)\) plane (see Figure 2), divides the domain of the elastic guess violating the composite yield function into two, domain 1 (shear failure) and domain 2 (tension failure), respectively (see Figure 2). If the stress point falls within domain 1, shear failure is declared, and the stress point is placed on the curve \(f^s\) = 0 using a flow rule derived using the potential function \(g^s\). If the point falls within domain 2, tensile failure takes place, and the new stress point satisfies \(f^t\) = 0 using a flow rule derived using \(g^t\).

Plastic Corrections

First, considering shear failure, partial differentiation of Equation (12) yields

(14)\[ {{\partial g^s}\over{\partial \tau}} = 1\]

(15)\[ {{\partial g^s}\over{\partial \sigma}} = q_{\psi}\]

Substitution of \(\partial g^s / \partial \tau\) and \(\partial g^s / \partial \sigma\) for \(\Delta {\gamma}^e\) and for \(\Delta {\epsilon}^e\), respectively, in Equation (7) and Equation (8) gives

(16)\[ S_1 \left( {{\partial g^s}\over{\partial \tau}}, {{\partial g^s}\over{\partial \sigma}} \right) = G\]

(17)\[ S_2 \left({{\partial g^s}\over{\partial \tau}}, {{\partial g^s}\over{\partial \sigma}} \right) = K q_{\psi}\]

Using \(f = f^s\) (see Equation (9)) then become

(18)\[ {\tau}^N = {\tau}^I - {\lambda}^s\ G\]

(19)\[ {\sigma}^N = {\sigma}^I - {\lambda}^s\ K\ q_{\psi}\]

and

(20)\[ {\lambda}^s = {{f^s ({\tau}^I, {\sigma}^I)}\over{G + K q_{\phi}\ q_{\psi}}}\]

The new stress tensor components may be expressed in terms of the generalized stresses using a rescaling technique. Formally, we may write Equation (18) as

(21)\[ {\tau}^N = \mu\ {\tau}^I\]

where \(\mu\) is a known proportionality factor (\(\mu = 1 - {\lambda}^s G / {\tau}^I\)). From the definition Equation (1) of \(\tau\) in terms of the tensor components \(s_{ij}\), we then have

(22)\[ {s_{ij}}^N = \mu\ {s_{ij}}^I\]

Eliminating \(\mu\) from the last two expressions, we obtain

(23)\[ {s_{ij}}^N = {s_{ij}}^I\ \ {{{\tau}^N}\over{{\tau}^I}}\]

Finally, new stress components may be calculated from Equation (19) and Equation (24) using the definition

(24)\[ {{\sigma}_{ij}}^N = {s_{ij}}^N + {\sigma}^N\ {\delta}_{ij}\]

We now consider tensile failure. Partial differentiation of Equation (13) gives

(25)\[ {{\partial g^t}\over{\partial \tau}} = 0\]

(26)\[ {{\partial g^t}\over{\partial \sigma}} = 1\]

Using Equation (7), we obtain

(27)\[ S_1 \left( {{\partial g^t}\over{\partial \tau}}, {{\partial g^t}\over{\partial \sigma}} \right) = 0\]

(28)\[ S_2 \left( {{\partial g^t}\over{\partial \tau}}, {{\partial g^t}\over{\partial \sigma}} \right) = K\]

With \(f = f^t\), as given by Equation (10):

(29)\[ {\tau}^N = {\tau}^I\]

(30)\[ {\sigma}^N = {\sigma}^I - {\lambda}^t K\]

and

(31)\[ {\lambda}^t = {{{\sigma}^I - {\sigma}^t}\over{K}}\]

As expected, after substitution of Equation (31) into Equation (30), we obtain

(32)\[ {\tau}^N = {\tau}^I\]

(33)\[ {\sigma}^N = {\sigma}^t\]

In this mode of failure, \({s_{ij}}^N = {s_{ij}}^I\), and we may write, from the definition of deviatoric stresses and Equation (33),

(34)\[ {{\sigma}_{ij}}^N = {s_{ij}}^I + {\sigma}^t\ {\delta}_{ij}\]

from which it follows that

(35)\[ {{\sigma}_{ij}}^N = {{\sigma}_{ij}}^I + ({\sigma}^t - {\sigma}^I) \ {\delta}_{ij}\]

Apex Stress Correction

It is possible that \(\sigma\) is greater than the apex stress (\(q_k/q_{\phi}\)) at an extreme circumstance when \(q_{\phi}\) is not zero (usually after shear plastic corrections). Once this occurs, the stress will be forced to the apex, or \(\sigma = q_k/q_{\phi}\) and \(\tau=0\).

Implementation Procedure

In the implementation of the Drucker-Prager model in FLAC3D, an elastic guess, \({\sigma}_{ij}^I\), is first computed by adding to the old stress components, increments calculated by application of Hooke’s law to the total strain increments, \(\Delta {\epsilon}_{ij}\) (see Elastic Model). Deviatoric stresses, \(s_{ij}^I\), are evaluated from \({\sigma}_{ij}^I\), and the elastic guess \(({\tau}^I, {\sigma}^I)\) is derived from \(s_{ij}^I\) and \({\sigma}_{ij}^I\) using Equations (1) and (2).

If this guess violates the composite yield criterion (see Equations (9) and (10)), then either in domain 1 or in domain 2 (see Figure 2). In the first case, shear failure takes place, and \({\tau}^N\) and \({\sigma}^N\) are evaluated from Equations (18) and (19), using Equation (20). New deviatoric stress components are derived using Equation (23) and, finally, new stress components are calculated from Equation (24). In the second case, tensile failure occurs, and new stress components are evaluated from Equation (35).

If the point \(({\tau}^I, {\sigma}^I)\) is located below the composite failure envelope, no plastic flow takes place for this step, and the new stresses are given by \({\sigma}_{ij}^I\).

Note that the tensile strength default value is zero for a material with \(q_{\phi}\) = 0, and is \({\sigma}_{max}^t\) otherwise (see Equation (11)). This last value will be substituted for \({\sigma}^t\) if the assigned value for the tensile strength exceeds \({\sigma}_{max}^t\). There is no tensile softening in this model.

Notes on Parameters

The Drucker-Prager model in FLAC3D is described by means of four parameters: \(q_{\phi}, k_{\phi}, q_{\psi}\), and \({\sigma}^t\). The particular case \(q_{\phi}\) = 0, \(f^s\) = 0 gives the von Mises criterion. By appropriate adjustment of the parameters, the criterion may also be fitted to approximate the geometry of the Mohr-Coulomb or Tresca criterion in the (\(\tau,\sigma\))-plane. (These last criteria are addressed in the next section.)

The Drucker-Prager shear criterion \(f^s\) = 0 is represented in the principal stress space \(({\sigma}_1, {\sigma}_2, {\sigma}_3)\) by a cone with axis along \({\sigma}_1 = {\sigma}_2 = {\sigma}_3\) and apex at \(({\sigma}_1, {\sigma}_2, {\sigma}_3) = (a, a, a)\), with \(a = k_{\phi} / q_{\phi}\) (see Figure 3). The Mohr-Coulomb criterion, characterized by two parameters (cohesion, \(c\), and friction angle, \(\phi\)), is represented there by an irregular hexagonal pyramid with the same axis and three “outer” and three “inner” edges (see Figure 4).

The parameters \(q_{\phi}\) and \(k_{\phi}\) can be adjusted so that the Drucker-Prager cone will pass through either the outer or the inner edges of the Mohr-Coulomb pyramid.

For the outer adjustment, we have

(36)\[ q_{\phi} = {{6}\over{\sqrt{3} (3 - \sin{\phi})}} \sin{\phi}\]

(37)\[ k_{\phi} = {{6}\over{\sqrt{3} (3 - \sin{\phi})}} c \cos{\phi}\]

For the inner adjustment, we have

(38)\[ q_{\phi} = {{6}\over{\sqrt{3} (3 + \sin{\phi})}} \sin{\phi}\]

(39)\[ k_{\phi} = {{6}\over{\sqrt{3} (3 + \sin{\phi})}} c \cos{\phi}\]

For the average adjustment (of outer and inner adjustments), we have

(40)\[ q_{\phi} = {{6\sqrt{3}}\over{(9 - \sin^2{\phi})}} \sin{\phi}\]

(41)\[ k_{\phi} = {{6\sqrt{3}}\over{(9 - \sin^2{\phi})}} c \cos{\phi}\]

For a compromised adjustment so that the Drucker-Prager circle area is identical to the area of the Mohr-Coulomb irregular hexagon in the \(\pi\) plane, we have

(42)\[ q_{\phi} = {{6\sqrt{3}}\over{\sqrt{2\sqrt{3}\pi(9 - \sin^2{\phi})}}} \sin{\phi}\]

(43)\[ k_{\phi} = {{6\sqrt{3}}\over{\sqrt{2\sqrt{3}\pi(9 - \sin^2{\phi})}}} c \cos{\phi}\]

In the special case \(q_{\phi}\) = 0, the Drucker-Prager criterion degenerates into the von Mises criterion, which corresponds to a cylinder in the principal stress space. The Tresca criterion is a special case of the Mohr-Coulomb criterion for which \(\phi\) = 0. It is represented in the principal stress space by a regular hexagonal prism. The von Mises cylinder circumscribes the prism for

(44)\[ q_{\phi} = 0\]

(45)\[ k_{\phi} = {{2}\over{\sqrt{3}}} c\]

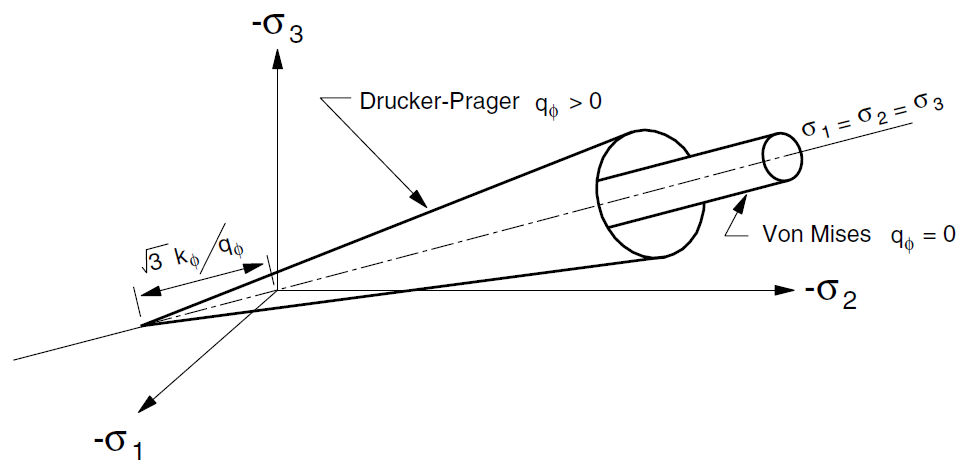
Figure 3: Drucker-Prager and von Mises yield surfaces in principal stress space.

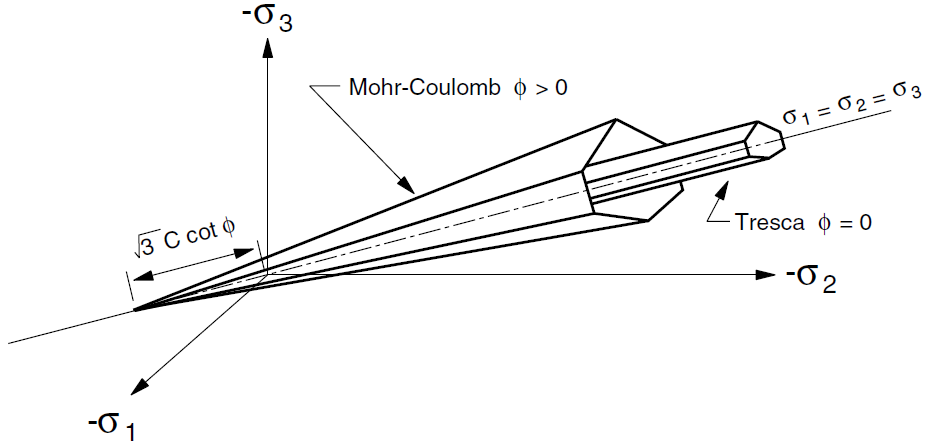
Figure 4: Mohr-Coulomb and Tresca yield surfaces in principal stress space.

drucker-prager Model Properties

Use the following keywords with the zone property (FLAC3D) or block zone property (3DEC) command to set these properties of the Drucker-Prager model.

drucker-prager

bulk f

bulk modulus, \(K\)

cohesion-drucker f

material parameter, \(k_{\phi}\)

dilation-drucker f

material parameter, \(q_{\psi}\). The default is 0.0.

friction-drucker f

material parameter, \(q_{\phi}\)

poisson f

Poisson’s ratio, \(\nu\)

shear f

shear modulus, \(G\)

tension f

tension limit, \({\sigma}^t\). The default is 0.0.

young f

Young’s modulus, \(E\)

Notes

• Only one of the two options is required to define the elasticity: bulk modulus \(K\) and shear modulus \(G\), or Young’s modulus \(E\) and Poisson’s ratio \(\nu\). When choosing the latter, Young’s modulus \(E\) must be assigned in advance of Poisson’s ratio \(\nu\).

• The tension cut-off is \({\sigma}^t = min({\sigma}^t, k_{\phi} / q_{\psi})\).