FLAC3D Theory and Background • Constitutive Models

Von-Mises Model

The yield envelope for this model involves a von-Mises criterion. The position of a stress point on this envelope is controlled by an associated flow rule for shear failure.

Formulations

The yield function of the von-Mises model with kinematic hardening is defined as

(1) $$f^s = \left[ 1.5 (s_{ij}-\alpha_{ij}) (s_{ij}-\alpha_{ij}) \right]^{0.5} - \sigma_Y = 0$$

where the Einstein summation convention applies, $s_{ij}$ is the deviatoric stress tensor, $\alpha_{ij}$ is the back-stress tensor under the condition $\alpha_{ii}=0$), and $\sigma_Y$ is a positive material constant denoting yield strength under uniaxial conditions. Note that if there is no hardening, or $\alpha_{ij} = 0$, the yield function becomes

(2) $$f^s = q - \sigma_Y = 0$$

where $q = ( 1.5\ s_{ij} s_{ij} )^{0.5}$.

Incremental Elastic Law

The incremental expression of Hooke’s law, in terms of the generalized stress and stress increments, has the form

(3) $$\Delta s_{ij} = 2G \Delta e^e_{ij}$$

and

(4) $$\Delta p = -3K \Delta \varepsilon^e_v$$

where $p=-\sigma_{ii}/3$, $G$ is the elastic shear modulus, $K$ is the elastic bulk modulus, $e^e_{ij}$ is the elastic part of deviatoric strain tensor, and $\varepsilon^e_v$ is the elastic part of volumetric strain.

Composite Failure Criterion and Flow Rule

The potential function $g^s$ corresponds in general to an associated law, and has the form

(5) $$g^s = f^s$$

Hardening Rule

The hardening rule is assumed

(6) $$\Delta \alpha_{ij} = H \Delta \epsilon^p_{ij}$$

where $H$ is a material constant called kinematic plastics modulus. See the schematic in Figure 1 for the physical meaning of the plastic modulus in uniaxial loading.

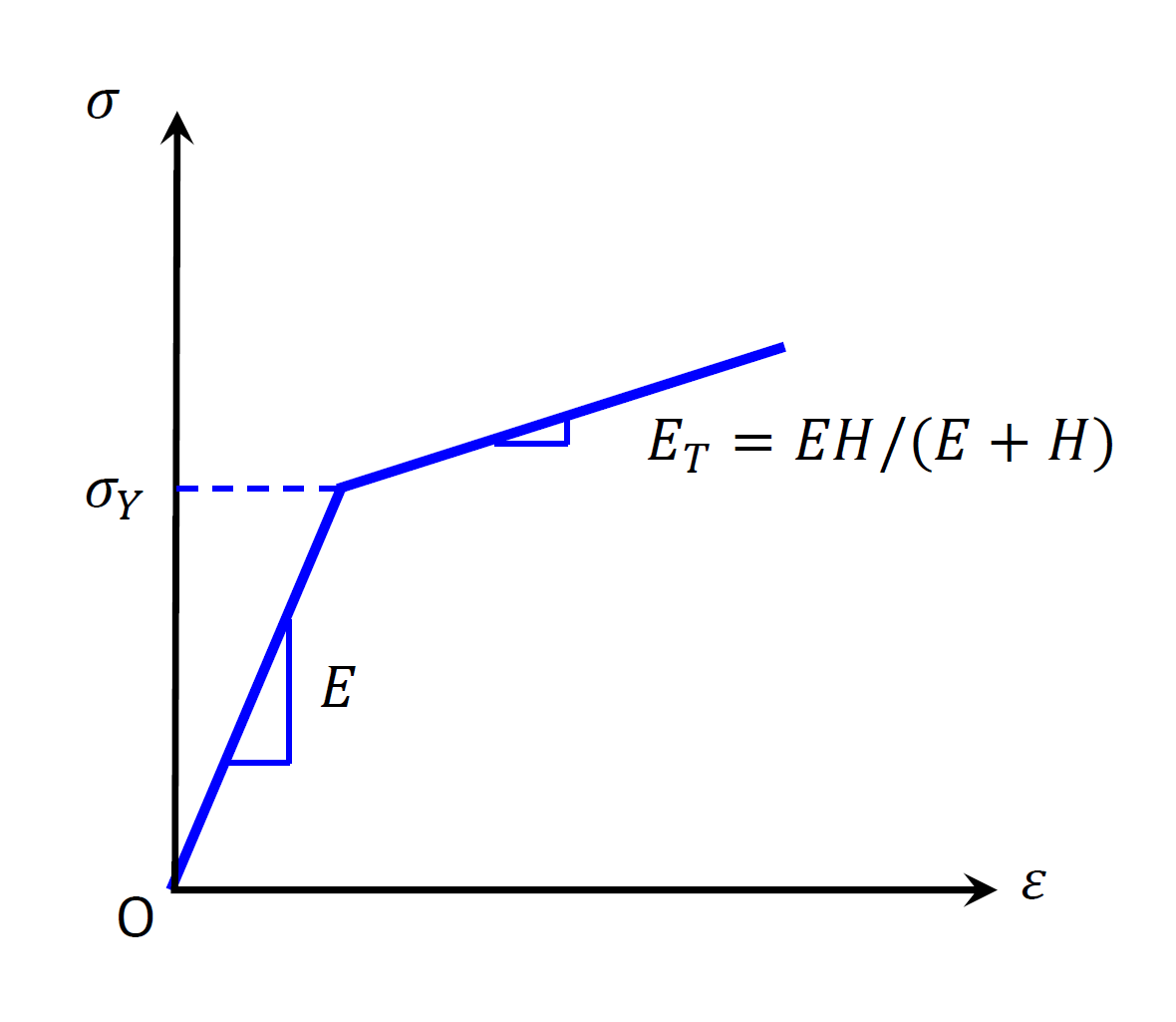
Figure 1: Von-Mises model in uniaxial loading.

Plastic Corrections

First, considering shear failure, partial differentiation of Equation (1) yields plastic strain

(7) $$\epsilon^p_{ij} = {\lambda}^s {{\partial g^s}\over{\partial \sigma_{ij}}} = {\lambda}^s {{1.5(s_{ij}-\alpha_{ij})}\over{[ 1.5(s_{ij}-\alpha_{ij}) (s_{ij}-\alpha_{ij})]^{0.5}}}$$

apparently, $\varepsilon^p_v = 0$, and $e^p_{ij} = \epsilon^p_{ij}$.

The consistency condition of yield function

(8) $$\Delta f^s(s^I_{ij} + \Delta s_{ij}, \alpha^I_{ij} + \Delta \alpha_{ij}) = 0$$

yields

(9) $${\lambda}^s = {{f^s(s^I_{ij}, \alpha^I_{ij})} \over {3G+H}}$$

von-mises Model Properties

Use the following keywords with the zone property (FLAC3D) or block zone property (3DEC) command and with the structure shell property (or liner/geogrid) command to set these properties of the von Mises model.

von-mises

bulk f

bulk modulus, $K$

modulus-plastic f

kinematic plastic (hardening) modulus, $H$ (see Figure 2). The default value is zero. Be aware that this is not the elastoplastic tangent modulus, $E_t$. The relationship between $H$ and $E_t$ is shown in Figure 2.

poisson f

Poisson’s ratio, $\nu$

shear f

shear modulus, $G$

strength-yield f

yield strength, $\sigma_Y$

young f

Young’s modulus, $E$

Notes

• Only one of the two options is required to define the elasticity: bulk modulus $K$ and shear modulus $G$, or Young’s modulus $E$ and Poisson’s ratio $\nu$. When choosing the latter, Young’s modulus $E$ must be assigned in advance of Poisson’s ratio $\nu$.

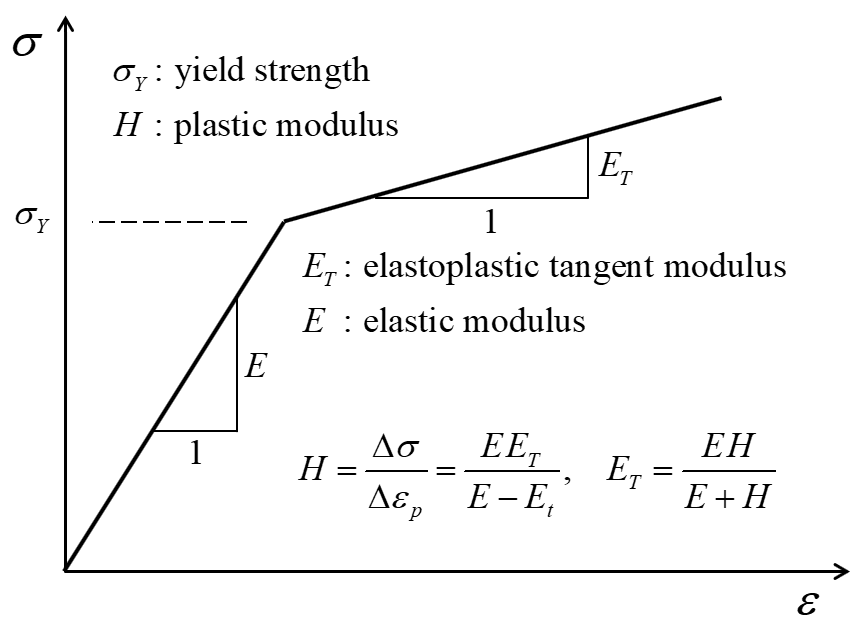
Figure 2: Behavior of von Mises model when subjected to uniaxial loading.