FLAC3D Theory and Background • Constitutive Models

Strain-Softening/Hardening Mohr-Coulomb (SSoft) Model

This model is based on the Mohr-Coulomb model with non-associated shear and associated tension flow rules, as described earlier. The difference, however, lies in the possibility that the cohesion, friction, dilation, and tensile strength may soften or harden after the onset of plastic yield. In the Mohr-Coulomb model, those properties are assumed to remain constant. Here, the user can define the cohesion, friction and dilation as piecewise-linear functions of a hardening parameter measuring the plastic shear strain. A piecewise-linear softening law for the tensile strength can also be prescribed in terms of another hardening parameter measuring the plastic tensile strain. The code measures the total plastic shear and tensile strains by incrementing the hardening parameters at each timestep, and causes the model properties to conform to the user-defined functions.

Formulations

The yield and potential functions, plastic flow rules, and stress corrections are identical to those of the Mohr-Coulomb model.

Hardening Parameters

The two hardening parameters for this model (\({\kappa}^s\) and \({\kappa}^t\)) are defined as the sum of some incremental measures of plastic shear and tensile strain for the zone, respectively. The zone-shear and tensile-hardening increments are calculated as the volumetric average of hardening increments over all tetrahedra involved in the zone.

The shear-hardening increment for a particular tetrahedron is a measure of the second invariant of the plastic shear-strain increment tensor for the step, given as

(1)\[\Delta {\kappa}^s = {{1}\over{\sqrt 2}} \sqrt{(\Delta {\epsilon}_1^{p_s} - \Delta {\epsilon}_m^{p_s})^2 + (\Delta {\epsilon}_m^{p_s})^2 + (\Delta {\epsilon}_3^{p_s} - \Delta {\epsilon}_m^{p_s})^2}\]

where \(\Delta {\epsilon}_m^{p_s}\) is the mean plastic strain increment,

(2)\[\Delta {\epsilon}_m^{p_s} = {{1}\over{3}} (\Delta {\epsilon}_1^{p_s} + \Delta {\epsilon}_3^{p_s})\]

The tetrahedron tensile-hardening increment is the magnitude of the plastic tensile-strain increment,

(3)\[\Delta {\kappa}^t = |\Delta {\epsilon}_3^{p_t}|\]

Plastic-Strain Increments

The plastic-strain increments involved in the preceding formula may be derived from the definition \(\Delta {\underline{\epsilon}}_i^p = \lambda {{\partial g}\over{\partial {\underline{\sigma}}_i}}\) of the flow rule. They have the form

(4)\[\Delta {\epsilon}_1^{p_s} = {\lambda}^s\]

(5)\[\Delta {\epsilon}_3^{p_s} = - {\lambda}^s N_{\psi}\]

(6)\[\Delta {\epsilon}_3^{p_t} = {\lambda}^t\]

where \({\lambda}^s\) and \({\lambda}^t\) are given by the Mohr-Coulomb model.

User-Defined Functions for Cohesion, Friction, Dilation, and Tensile Strength

User-defined functions for zone yielding parameters can be determined by back-analysis of the post-failure behavior of a material. Consider a one-dimensional stress-strain curve, \(\sigma\) versus \(\epsilon\), which softens upon yield and attains some residual strength (Figure 1).

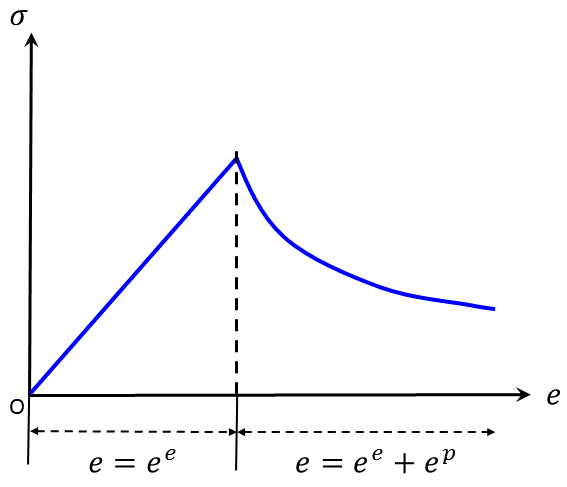
Figure 1: Example stress-strain curve.

The curve is linear to the point of yield; in that range, the strain is elastic only: \(\epsilon = \epsilon^e\). After yield, the total strain is composed of elastic and plastic parts: \(\epsilon = \epsilon^e + \epsilon^p\). In the softening/hardening model, the user defines the cohesion, friction, dilation, and tensile strength variance as a function of the plastic portion, \(\epsilon^p\), of the total strain. These functions, which could in reality be sketched as indicated in Figure 2, are approximated in FLAC3D as sets of linear segments (Figure 3).

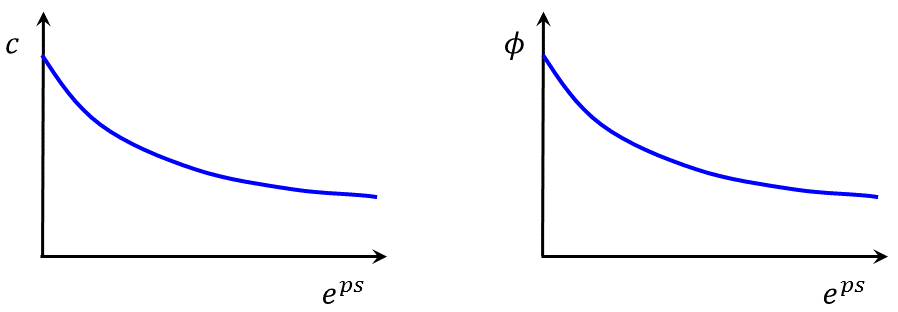
Figure 2: Variation of cohesion (a) and friction angle (b) with plastic strain.

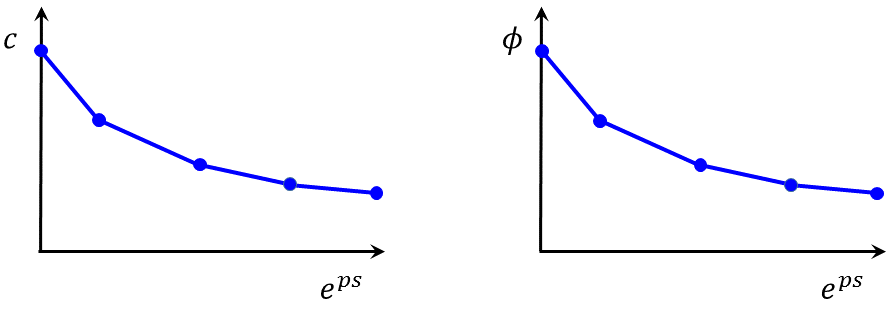
Figure 3: Approximation by linear segments.

Hardening and softening behaviors for the cohesion, friction, and dilation in terms of the shear parameter \(\Delta \epsilon^{ps}\) (see Equation (1)) are provided by the user in the form of tables. Each table contains pairs of values: one for the parameter, and one for the corresponding property value. It is assumed that the property varies linearly between two consecutive parameter entries in the table. Softening of the tensile strength is described in a similar manner, using the parameter \(\Delta \epsilon^{pt}\) (see Equation (2)).

Implementation Procedure

The implementation of the strain-softening/hardening model in FLAC3D/3DEC proceeds as indicated in the Mohr-Coulomb model description. After determination of the new stresses for the step, the hardening parameters for the zone are updated following the procedure described above. If appropriate, these parameters are then used to determine new values for the zone cohesion, friction, dilation, and tensile strength.

Note that the tensile strength of the material can only decrease. Also, for material with friction, the value cannot exceed the maximum value \({\sigma}_{max}^t\).

strain-softening model properties

Use the following keywords with the zone property (FLAC3D) or block zone property (3DEC) command and with the structure shell property (or liner/geogrid) command to set these properties of the strain-softening/hardening Mohr-Coulomb model.

strain-softening

bulk f

elastic bulk modulus, \(K\)

cohesion f

cohesion, \(c\)

dilation f

dilation angle, \(\psi\). The default is 0.0.

friction f

internal angle of friction, \(\phi\)

poisson f

Poisson’s ratio, \(\nu\)

shear f

elastic shear modulus, \(G\)

tension f

tension limit, \(\sigma^t\). The default is 0.0.

young f

Young’s modulus, \(E\)

flag-brittle b (a)

If true, the tension limit is set to 0 in the event of tensile failure. The default is false.

table-cohesion s (a)

name of the table relating cohesion to plastic shear strain

table_dilation s (a)

name of the table relating dilation angle to plastic shear strain

table-friction s (a)

name of the table relating friction angle to plastic shear strain

table-tension s (a)

name of the table relating tension limit to plastic tensile strain

strain-shear-plastic f (r)

accumulated plastic shear strain

strain-tension-plastic f (r)

accumulated plastic tensile strain

Key

(a) Advanced property.

This property has a default value; simpler applications of the model do not need to provide a value for it.

(r) Read-only property.

This property cannot be set by the user. Instead, it can be listed, plotted, or accessed through FISH.

Notes

• Only one of the two options is required to define the elasticity: bulk modulus \(K\) and shear modulus \(G\), or, Young’s modulus \(E\) and Poisson’s ratio \(\nu\). When choosing the latter, Young’s modulus \(E\) must be assigned in advance of Poisson’s ratio \(\nu\).

• The tension cut-off is \({\sigma}^t = min({\sigma}^t, c/\tan \phi)\).

• The tension table and flag-brittle should not be active at the same time.