Elastic Beam with Applied Moment (with shell elements)

Problem Statement

Note

To view this project in FLAC3D, use the menu command Help ► Examples…. Choose “Structure/Shell/AppliedMomentShell” and select “AppliedMomentShell.prj” to load. The data file used is shown at the end of this example.

The tip deflection for a cantilever beam with a moment at its tip is computed and compared with the analytical solution for an Euler-Bernoulli beam. The problem is modeled with Euler-Bernoulli beam elements in Elastic Beam with Applied Moment. The problem is here modeled with DKT-CST Hybrid shell elements. This problem is an example of geometric nonlinearity, whereby deformations significantly alter the location of loads, so that equilibrium equations must be written with respect to the deformed geometry. Such problems can be solved by running FLAC3D in large-strain mode.

Analytical Solution

The analytical solution is given in Elastic Beam with Applied Moment. The solution corresponds with simple beam theory assumptions. Ugural (1981, p. 8) describes how these assumptions differ for plate theory:

\(\ldots\) if a plate element of unit width and parallel to the beam axis were free to move sidewise under transverse loading, the top and bottom surfaces would be deformed into saddle-shaped or anticlastic surfaces \(\ldots\) The flexural rigidity would then be \(E t^3 / 12\), as in the case of a beam. The remainder of the plate prevents the anticlastic curvature however. Owing to this action, a plate manifests greater stiffness than a beam by a factor \(1 / (1 - \nu^2) \ldots\)

For the present problem, we need to set Poisson’s ratio of the plate equal to zero in order to match the solution from simple beam theory.[1]

Particular Problem

The particular problem to be considered is defined as follows. The plate has a 10-m length, 1-m width and 100-mm thickness. The plate is comprised of structural steel, and is assumed to behave as an isotropic elastic material with

\[E = 200 \textrm{ GPa}, \quad \nu = 0.30\]

The Young’s modulus of the plate is set to \(E\), and the Poisson’s ratio of the plate is set to zero (for the reason cited above). The moment \((M = 2 \times 10^6 \textrm{ Nm})\) is applied at the beam tip — one-half of this value is assigned to each of the two nodes at the tip. For these properties, the tip deflection is \(5.31529 \textrm{ m}\).

FLAC3D Model

The beam is modeled as a finite-sized rectangular plate of length \((L)\), width \((b)\) and thickness \((d)\) using a 10 by 1 mesh of DKT-CST Hybrid shell elements with a cross-diagonal pattern as shown in Figure 1. The cross-diagonal pattern is used to ensure symmetric response. A fixed support is specified at the left end by restricting translation and rotation (in all degrees of freedom) of the nodes at the left end. A moment vector aligned with the \(z\) direction is applied to the nodes at the tip, with one-half of the total value assigned to each node. The \(y\)-displacement at the tip is monitored as a history. Local nonviscous damping is used with a damping factor of 0.8. The model is run in large-strain mode to capture the geometric nonlinearity. The model is cycled until a convergence limit of \(1 \times 10^{-3}\) is achieved.

Figure 1: Geometry of the FLAC3D model showing mesh with nodes and global coordinate system.

Results and Discussion

The deformed shape and tip-deflection history are shown in Figure 2, from which we conclude that the static solution has been obtained. The tip deflection equals \(5.30139 \textrm{ m}\), which is within 0.26% of the analytical solution.

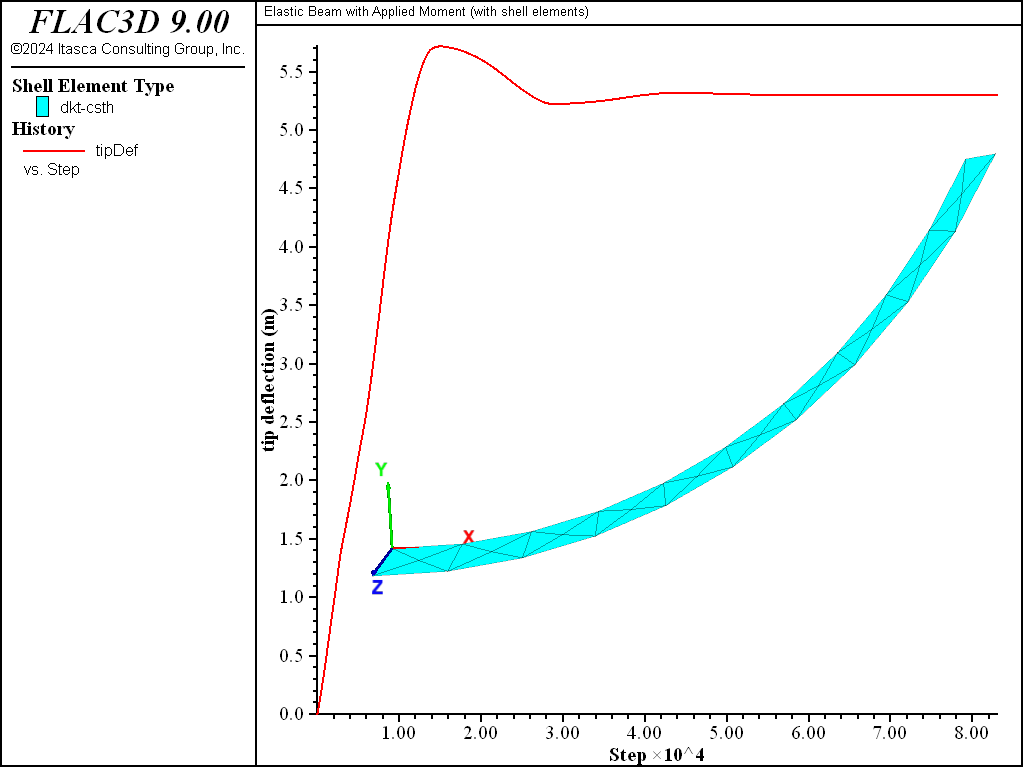
Figure 2: Final configuration and tip deflection.

References

Ugural, A. C. Stresses in Plates and Shells. New York: McGraw-Hill Publishing Company Inc. (1981).

Endnotes

[1]

The Poisson’s ratio enters into the simple beam theory solution only for torsional loading. Such loading is absent in the present problem, thus, we are free to set Poisson’s ratio of the plate equal to zero so that the plate behaves like a beam.

Data File

AppliedMomentShell.dat

model new
model title 'Elastic Beam with Applied Moment (with shell elements)' 

; Create shell and assign properties.
structure shell create by-quadrilateral (0,0,0) (10,0,0) (10,0,1) (0,0,1) size (10,1) ...
                    cross-diagonal element-type dkt-csth
structure shell property thickness 0.1
structure shell cmodel assign elastic
structure shell property young 200e9 poisson 0.0

; Apply boundary conditions.
structure node fix velocity rotation  range position-x 0.0  ; fully fix left end
structure node apply moment (0,0,1e6) range position-x 10.0 ; apply moment at tip

; Monitor history of tip deflection (the node on back edge, z=0).
structure node history name 'tipDef' displacement-y position (10.0, 0, 0)

model save 'initialConfig'

model large-strain on
model solve convergence 1e-3
model save 'AppliedMomentShell'