Dynamic Damping
Natural dynamic systems contain some degree of damping of the vibration energy within the system; otherwise, the system would oscillate indefinitely when subjected to driving forces. Damping is due, in part, to energy loss as a result of internal friction in the intact material and slippage along interfaces, if these are present.
FLAC3D uses a dynamic algorithm for solution of two general classes of mechanical problems: quasi-static and dynamic. Damping is used in the solution of both classes of problems, but quasi-static problems require more damping for rapid convergence to equilibrium. The damping for static solutions is discussed in Mechanical Damping.
For a dynamic analysis, the damping in the numerical simulation should reproduce, in magnitude and form, the energy losses in the natural system when subjected to a dynamic loading. In soil and rock, natural damping is mainly hysteretic (i.e., independent of frequency—see Gemant and Jackson 1937, and Wegel and Walther 1935). It is difficult to reproduce this type of damping numerically because of at least two problems (see Cundall 1976, and comments in Characteristics of Fully Nonlinear Method). First, many simple hysteretic functions do not damp all components equally when several waveforms are superimposed. Second, hysteretic functions lead to path-dependence, which makes results difficult to interpret. However, if a constitutive model that contains an adequate representation of the hysteresis that occurs in a real material is found, then no additional damping would be necessary. This comment is addressed to users who program their own constitutive models in C++; the built-in models are not considered to model dynamic hysteresis well enough to omit additional damping completely.
For several reasons, it is impractical to use the “real” stress/strain response of the material in numerical simulations. For example: 1) there are no laws that describe the complete material response; and 2) existing laws that capture many important aspects have many material parameters requiring extensive calibration.
In time-domain programs, Rayleigh damping is commonly used to provide damping that is approximately frequency-independent over a restricted range of frequencies. Although Rayleigh damping embodies two viscous elements (in which the absorbed energy is dependent on frequency), the frequency-dependent effects are arranged to cancel out at the frequencies of interest.
Hysteretic damping is an alternative damping option. This form of damping allows strain-dependent modulus and damping functions to be incorporated directly into the FLAC3D simulation. This makes it possible to make direct comparisons between calculations made with the equivalent-linear method and a fully nonlinear method, without making any compromises in the choice of constitutive model.
For routine engineering design, we must use an approximate representation of cyclic energy dissipation. In FLAC3D, when using simple plasticity models such as Mohr-Coulomb, the choice is between Rayleigh damping and hysteretic damping. Here, we make some general comparisons between the two approaches, enabling a choice to be made. In general, hysteretic damping is the more realistic of the two, and it entails no reduction in timestep. For further discussion, see Integration of Damping Schemes and Nonlinear Material Models for Geo-materials.
For low levels of cyclic strain and fairly uniform conditions, Rayleigh damping and hysteretic damping give similar results, provided that the levels of damping set for both are consistent with the levels of cyclic strain experienced. The results will differ in the following two circumstances:
When the system is nonuniform (e.g., layers of quite different properties), then cyclic strain levels may be different in different locations and at different times. Using hysteretic damping, these different strain levels produce realistically different damping levels in time and space, while constant and uniform Rayleigh damping parameters can only reproduce the average response. It would be possible to adjust the Rayleigh damping parameters to account for spatial variations in damping using an iterative (strain-compatible) scheme, as used in the equivalent-linear method. It may also be possible to adjust the Rayleigh damping parameters in time, although some practical difficulties may be encountered.
As yield is approached, neither Rayleigh damping nor hysteretic damping account for the energy dissipation of extensive yielding. Thus, irreversible strain occurs externally to both schemes, and dissipation is represented by the yield model (e.g., Mohr-Coulomb). Under this condition, the mass-proportional term of Rayleigh damping may inhibit yielding because rigid-body motions that occur during failure modes are erroneously resisted. Hysteretic damping may give rise to larger permanent strains in such a situation, but this condition is usually believed to be more realistic compared to one using Rayleigh damping.
We note that hysteretic damping provides almost no energy dissipation at very low cyclic strain levels, which may be unrealistic. To avoid low-level oscillation, it is recommended that a small amount (e.g., 0.2%) of stiffness-proportional Rayleigh damping be added when hysteretic damping is used in a dynamic simulation.
Another form of damping in FLAC3D, the local damping embodied in FLAC3D’s static solution scheme, may be used dynamically, but with a damping coefficient appropriate to wave propagation. Local damping in dynamic problems is useful as an approximate way to include hysteretic damping. However, it becomes increasingly unrealistic as the complexity of the waveforms increases (i.e., as the number of frequency components increases). Local damping cannot properly capture the energy loss of multiple frequency cyclic loading.
A fourth form of damping, artificial viscosity, is also provided in FLAC3D. This damping may be used for analyses involving sharp dynamic fronts.
Rayleigh Damping
Formulation
Rayleigh damping was originally used in the analysis of structures and elastic continua to damp the natural oscillation modes of the system. The equations, therefore, are expressed in matrix form.
A damping matrix, \(C\), is used with components proportional to the mass, \(M\), and stiffness, \(K\), matrices:
where \(\alpha\) is the mass-proportional damping constant; and \(\beta\) is the stiffness-proportional damping constant.
The mass-proportional term is analogous to a dashpot connecting every FLAC3D gridpoint to “ground.” The stiffness-proportional term is analogous to a dashpot connected across each FLAC3D zone (responding to the strain rate). Although both terms are frequency-dependent, an approximately frequency-independent response can be obtained over a limited frequency range with the appropriate choice of parameters as discussed below.
For a multiple degree-of-freedom system, the critical damping ratio, \(\xi_i\), at any angular frequency of the system, \(\omega_i\), can be found from (Bathe and Wilson 1976)
or
The critical damping ratio, \(\xi_i\), is also known as the fraction of critical damping for mode \(i\) with angular frequency \(\omega_i\).
Figure 1 shows the variation of the normalized critical damping ratio with angular frequency \(\omega_i\). Three curves are given: mass components only; stiffness components only; and the sum of both components. As shown, mass-proportional damping is dominant at lower angular-frequency ranges, while stiffness-proportional damping dominates at higher angular frequencies. The curve representing the sum of both components reaches a minimum at
or
The center frequency is then defined as
Note that at frequency \(\omega_{\min}\) (or \(f_{\min}\)) (and only at that frequency), mass damping, and stiffness damping each supply half of the total damping force.
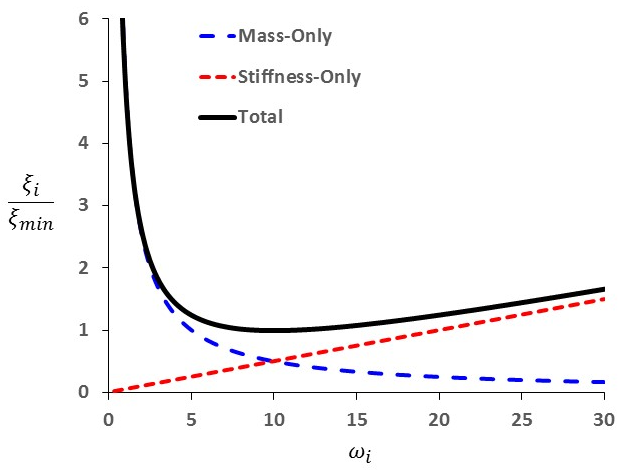
Figure 1: Variation of normalized critical damping ratio with angular frequency.
Rayleigh damping is specified in FLAC3D with the parameters \(f_{\min}\) in Hertz (cycles per second) and \(\xi_{\min}\), both specified with the zone dynamic damping rayleigh command.
Stiffness-proportional damping causes a reduction in the critical timestep for the explicit solution scheme (see Belytschko 1983). As the damping ratio corresponding to the highest natural frequency is increased, the timestep is reduced (see Dynamic Timestep). This can result in a substantial increase in runtimes for dynamic simulations.
In FLAC3D, the internal timestep calculation takes account of stiffness-proportional damping, but it is still possible for instability to occur if the large-strain calculation is in effect (model large-strain) and very large mesh deformation occurs. If this happens, it is necessary to reduce the timestep manually (via the model dynamic timestep fix command).
For the case shown in Figure 1, \(\omega_{\min} = 10\) radians per second. It is evident that the damping ratio is almost constant over at least a 3:1 frequency range (e.g., from 5 to 15). Since damping in geologic media is commonly independent of frequency (as discussed in Dynamic Mechanical Damping), \(\omega_{\min}\) is usually chosen to lie in the center of the range of frequencies present in the numerical simulation — either natural frequencies of the model or predominant input frequencies. Hysteretic damping is thereby simulated in an approximate fashion.
Viscous stress increments representing the stiffness-proportional component of Rayleigh damping are added to the total stress increments during a timestep in order to compute gridpoint forces. Thus,
where \(\sigma_v\) is a component of the combined stress tensor used to derive gridpoint forces, \(\sigma_n\) is the corresponding component returned from the constitutive law, and \(\sigma_o\) is the value of the component prior to invoking the constitutive law. The notation \(\bigl\{\) \(\bigr\}\) denotes the vector of all components.
Viscous stresses are not included with the accumulated total stresses (\(\sigma_n\)).
A stiffness matrix is not needed in this formulation. Rayleigh damping operates directly on the tangent modulus for the constitutive model, whether it is linear or nonlinear.
Stiffness-proportional damping is turned off when plastic failure occurs within a FLAC3D zone. Mass-proportional damping, however, remains active. If excessive failure occurs in a model, the mass-proportional term may inhibit yielding. In this case, it may be advisable to exclude Rayleigh damping from regions of strong plastic flow (by using the zone dynamic damping rayleigh command to set Rayleigh damping in selected regions, as described in Spatial Variation in Damping).
Guidelines for Selecting Rayleigh Damping Parameters
Damping Ratio, \(\xi_{\min}\)
What is normally attempted in a dynamic analysis is the reproduction of the frequency-independent damping of materials at the correct level. For geological materials, damping commonly falls in the range of 2 to 5% of critical; for structural systems, 2 to 10% is representative (Biggs 1964). Also, see Newmark and Hall (1982) for recommended damping values for different materials. In analyses that use one of the plasticity constitutive models (e.g., Mohr-Coulomb), a considerable amount of energy dissipation can occur during plastic flow. Thus, for many dynamic analyses that involve large-strain, only a minimal percentage of damping (e.g., 0.5%) may be required. Further, dissipation will increase with amplitude for stress/strain cycles that involve plastic flow. \(\xi_{\min}\) is adjusted to coincide with the correct physical damping ratio.
The equivalent-linear program SHAKE (Schnabel, Lysmer, and Seed 1972) can be used to estimate material damping to represent the inelastic cyclic behavior of soils. An equivalent-linear analysis is performed for a layered soil deposit using the shear wave speeds and densities for the different layers. Strain-compatible values for the damping ratios and shear-modulus reduction factors are then determined. Average damping ratios and shear modulus reduction factors are estimated for each layer; the damping ratios are the estimates for input in the Rayleigh damping in FLAC3D.
Center Frequency, \(f_{\min}\)
Rayleigh damping is frequency-dependent but has a “flat” region that spans about a 3:1 frequency range, as shown in Figure 1. For any particular problem, a spectral analysis of typical velocity records might produce a response such as the one shown in Figure 2.
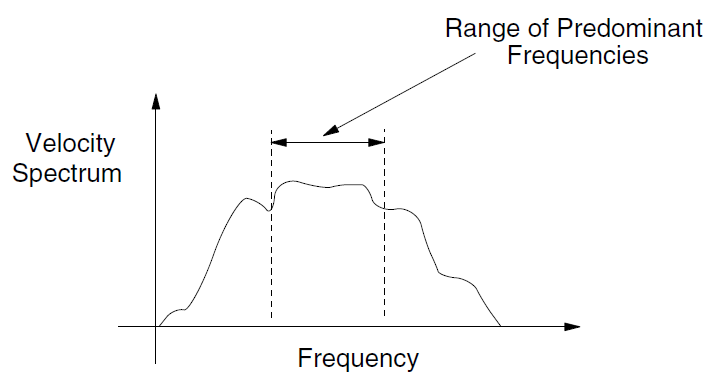
Figure 2: Plot of velocity spectrum versus frequency.
If the highest predominant frequency is three times greater than the lowest predominant frequency, then there is a 3:1 span or range that contains most of the dynamic energy in the spectrum. The idea in dynamic analysis is to adjust \(f_{\min}\) of the Rayleigh damping so that its 3:1 range coincides with the range of predominant frequencies in the problem. The predominant frequencies are neither the input frequencies nor the natural modes of the system, but a combination of both. The idea is to try to get the right damping for the important frequencies in the problem.
For many problems, the important frequencies are related to the natural mode of oscillation of the system. Examples of this type of problem include seismic analysis of surface structures such as dams, or dynamic analysis of underground excavations. The fundamental frequency, \(f\), associated with the natural mode of oscillation of a system is
where \(C\) is the speed of propagation associated with the mode of oscillation, and \(\lambda\) is the longest wavelength associated with the mode of oscillation.
For a continuous, elastic system (e.g., a one-dimensional elastic bar), the speed of propagation, \(C_p\), for \(p\)-waves is given by Equation (3), and for \(s\)-waves by Equation (4). If shear motion of the bar gives rise to the lowest natural mode, then \(C_s\) is used in the above equation; otherwise, \(C_p\) is used if motion parallel to the axis of the bar gives rise to the lowest natural mode.
The longest wavelength (or characteristic length or fundamental wavelength) depends on boundary conditions. Consider a solid bar of unit length with boundary conditions as shown in Figure 3a. The fundamental mode shapes for cases (1), (2), and (3) are as shown in Figure 3b. If a wavelength for the fundamental mode of a particular system cannot be estimated in this way, then a preliminary run may be made with zero damping (for example, see Mechanical Damping). A representative natural period may be estimated from time histories of velocity or displacement. Natural Periods of an Elastic Column contains a simple example in which natural periods are estimated by undamped simulations.
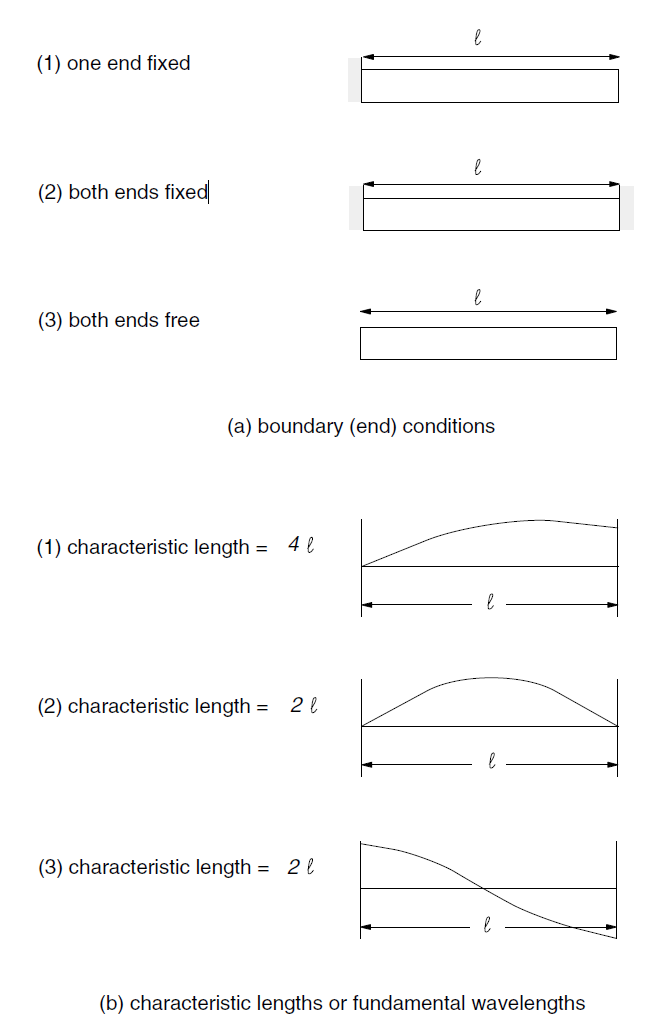
Figure 3: Comparison of fundamental wavelengths for bars with varying end conditions.
Example Application of Rayleigh Damping
In order to demonstrate how Rayleigh damping works in FLAC3D, the following simple example examines the results of four damping cases for comparison.
Maxwell Damping
Maxwell damping provides an alternative to Rayleigh damping for time-domain seismic deformation analyses. The numerical calculation time using Maxwell damping can be a small fraction of that required for Rayleigh damping. Maxwell damping makes practical large 3-D site response and soil-structure interaction analyses.
Using Rayleigh damping, a target damping ratio can obtain at two specific frequencies; the resulting damping is slightly smaller than the target damping ratio when the frequency is within the range bounded by these two specific frequencies, while damping becomes dramatically larger outside of this range. While Rayleigh damping is helpful to reduce artificial numerical high frequency noise, it can also over damp high frequency content because the damping ratio of the Rayleigh scheme can be more than 20% at high frequencies, even if it is low in the frequency range of interest. As pointed out by Hall (2006), the mass-proportional component of Rayleigh damping is essentially a non-physical mechanism and the stiffness-proportional component for softening materials can result in unrealistically large damping forces under certain conditions. Hall (2006), thus, suggested eliminating the mass-proportional damping contribution and bounding the stiffness-proportional damping contribution for Rayleigh damping. Another serious drawback of Rayleigh damping is the drastically reduced numerical time step. The stiffness damping component of Rayleigh damping leads to increasingly stiff response at higher frequencies, so that a smaller numerical time step is needed for stable numerical integration (Belytschko 1983). For large 3-D models with many degrees of freedom, the requirement of significantly longer machine calculation time makes the applications of the stiffness-proportional Rayleigh damping less practical.
Bielak et al. (2011) and others have shown that an improved form of damping for time-domain analyses can be developed by replacing the dashpot of stiffness damping, with one or more Maxwell components (a spring in series with a dashpot). While each Maxwell component produces frequency dependent damping, peaking at a particular frequency, a number of Maxwell components acting in parallel can be used to produce relatively constant damping over a desired frequency range. Dawson and Cheng (2021) implemented a practical Maxwell damping scheme with three components to provide small strain damping for time-domain seismic deformation analyses. It has been showed (Dawson and Cheng, 2021; Cheng and Dawson, 2022) that this scheme with three Maxwell components can produce relatively constant damping in the frequency range of interest for most seismic deformation analyses. Damping drops off gradually outside of this range.
Formulation
Standard Linear Solid
The basic building block of the Maxwell damping scheme is what is known as the Standard Linear Solid (SLS) as shown in Figure 4. This consists of a primary spring acting in parallel with a single Maxwell component – the Maxwell component itself being a spring in series with a viscous dashpot. Note that the stiffness of the Maxwell component spring is specified here as a fraction of the stiffness K of the primary spring.
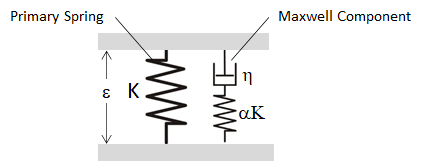
Figure 4: Standard Linear Solid, consisting of a primary spring in parallel with a Maxwell component (a spring in series with a viscous dashpot).
We first derive an expression for the complex (frequency domain) stiffness of the Maxwell component only. The differential equation describing the stress-strain response of the Maxwell component is:
where \(\alpha K\) is the spring stiffness and η is the viscosity. This differential equation can be solved by Fourier transform, or equivalently, by assuming harmonic motions of the form:
where \(\omega\) is the circular frequency and \(\varepsilon_0\) and \(\sigma_0\) are complex amplitudes, accounting for phase as well as magnitude. The complex stiffness, or modulus, of the Maxwell component is then
where
is the relaxation time, the ratio of viscosity to elastic stiffness. Dividing relation (12) by the stiffness K of the primary spring and using (13), results in the normalized, non-dimensional complex modulus for the Maxwell component
Next, consider the complex modulus of the Standard Linear Solid (Figure 4). Since the primary spring and the Maxwell component act in parallel, the stiffness of this system is simply the sum of the individual stiffnesses. The normalized complex modulus is then
or
The damping ratio for a viscoelastic material can be computed from the ratio of the imaginary and real parts of the complex stiffness (Bland, 1960), so that for the Standard Linear Solid, the damping ratio is:
It can be shown that maximum damping occurs at a circular frequency of
with a maximum damping value of
The damping versus frequency response of the SLS is illustrated in Figure 5 which shows the damping ratio for an SLS with 5% damping with a peak frequency of 3.5 Hz. The damping of the SLS has a narrow peak and broad tails.
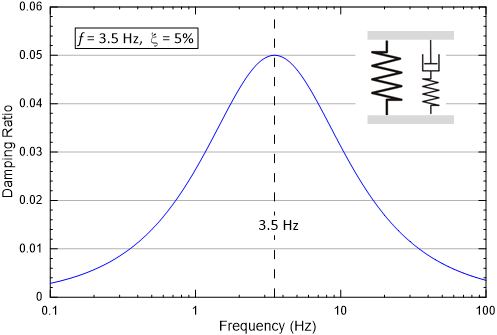
Figure 5: Damping ratio versus frequency for a Standard Linear Solid with a center frequency of 3.5 Hz and a peak damping of 5%.
Full Maxwell Damping Scheme
Next, we consider the full Maxwell damping scheme with three Maxwell components placed in parallel with the primary spring, as shown in Figure 6. Here the primary spring represents the elastic stiffness of the base constitutive model to which damping is to be added.
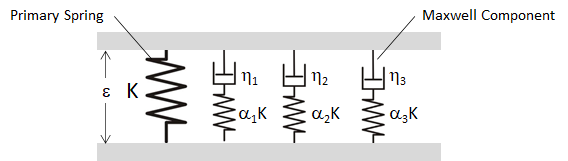
Figure 6: Maxwell damping scheme where three Maxwell components act in parallel with the primary spring.
According to Equation (14), the normalized complex stiffness of an individual Maxwell component with index k is
where
The normalized complex stiffness of the system as a whole, with a primary spring and three Maxwell components acting in parallel is then
and the damping ratio of the system is
With careful selection of the properties for the three Maxwell components, damping of the system can be made almost constant over a wide frequency range, as shown in Figure 7. Using three Maxwell components, relatively constant damping can be obtained between 0.5 Hz and 25 Hz, the relevant frequency range for most seismic deformation analyses. Outside this range, damping drops off gradually.
It can be seen in Figure 7 that damping of the system as a whole is approximately the superposition of the damping of the individual Maxwell components. This rough approximation provides a helpful starting point for selecting frequencies and damping values for the components to match a target damping value. Damping of the components can then be adjusted to obtain a closer fit. Figure 7 illustrates that this superposition is only approximate, as the peak damping for the 25 Hz component exceeds the damping of the combined system. In fact, there is interaction between the three components, as would be expected from Equation (16).
The lower damping at high frequencies shown in Figure 7 might be seen as a drawback of this technique, as time-domain numerical analyses can be subject to high-frequency numerical noise. However, high frequency vibrations, by definition, experience more cycles per unit time, with each cycle dissipating energy according to the damping ratio. Thus, high frequency noise can be damped out rapidly (in time) with even a very small damping ratio.
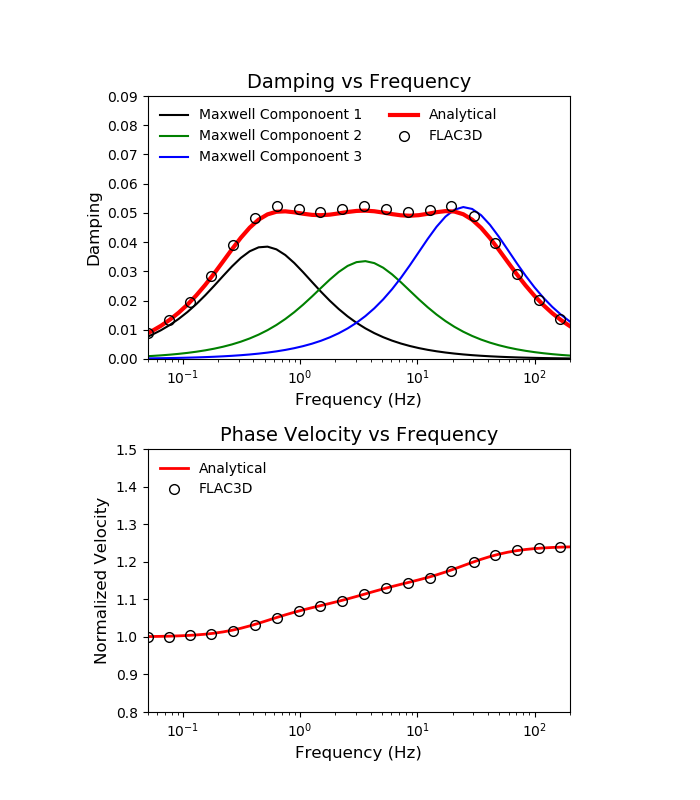
Figure 7: Damping ratio versus frequency for Maxwell damping scheme with three components: System damping, and damping of individual components.
User Inputs and Maxwell Component Properties
For specifying input properties for the damping scheme, it is convenient to think of the system as composed of three SLS, each consisting of a Maxwell component in parallel with the primary spring. Damping of the complete system is then very roughly the superposition of the damping of each of these SLS system. Convenient input parameters for the damping scheme are the center frequencies \(f_k\) (in hertz) of each SLS and the damping ratios \(\xi_k\) of each SLS. The \(\alpha_k\) constants can then be computed from the damping ratio with Equation (15), using the quadratic formula
The relaxation time for the individual Maxwell components is then
and the dashpot viscosities are
If pairs of \((f_k,\xi_k)\) are known, the closed-form solution for the target damping ratio can be straightforwardly obtained. However, calibration requires working in the opposite direction - finding pairs of \((f_k,\xi_k)\) that produce a suitable target damping ratio. A practical guideline is suggested here:
Select a target damping ratio, e.g., 5%.
Estimate a target frequency range over which the approximate target damping ratio is desired. The lower and upper bounds of this range is \(f_1\) and \(f_3\). Then \(f_2\) can be a value so that \(f_2 \approx \sqrt{f_1 f_3}\). For example, if we wish a target damping ratio of 0.05 and constant damping in the range of 0.5 and 25 Hz, then \(f_1\), \(f_2\), \(f_3\) can be 0.5, 3.5, 25 Hz, respectively. Generally, the frequency range of interest should cover the first primary natural frequency of the soil profile, the third primary natural frequency of the soil profile, and the dominate frequency of the input motion.
Using a plotting tool (e.g., Excel), adjust \((\xi_1,\xi_2,\xi_3)\) to approximate the target damping ratio over the target range. Experience has shown that with only a few trails, a satisfactory target damping ratio can be obtained.
Table 1 lists Maxwell component properties for various damping values, all fits using the same set of center frequencies. The resulting damping versus frequency curves are shown in Figure 8. Note that other values can be assigned to the center frequencies \(f_k\) in order to change the position or shape of the damping versus frequency curve.
Maxwell Component Properties |
|||
|---|---|---|---|
Damping |
\(f_1=0.5\) Hz |
\(f_2=3.5\) Hz |
\(f_3=25\) Hz |
\(\xi_1\) |
\(\xi_2\) |
\(\xi_3\) |
|
0.5% |
0.0039 |
0.0029 |
0.0041 |
1.0% |
0.0080 |
0.0060 |
0.0085 |
2.0% |
0.0160 |
0.0120 |
0.0180 |
3.0% |
0.0235 |
0.0190 |
0.0284 |
4.0% |
0.0311 |
0.0260 |
0.0398 |
5.0% |
0.0385 |
0.0335 |
0.0520 |
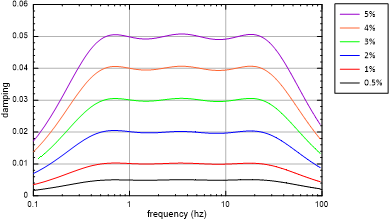
Figure 8: Damping ratio versus frequency for various Maxwell damping values.
Implementation
To provide low strain damping for linear elastic, as well as elasto-plastic constitutive models. Maxwell damping has also been implemented for structural elements such as beams, shells, cables and piles. The incremental equation describing the stress-strain response of a Maxwell component is:
where \(\Delta \varepsilon\) and \(\Delta t\) are known variables based on the FLAC3D dynamic implementation scheme. \(\sigma^n\), which is the stress of the Maxwell component calculated in the previous step, n, is also known. In order to calculate the stress of the Maxwell components in the current step, n+1, explicit or implicit algorithms can be employed.
Explicit Algorithm
If \(\sigma=\sigma^n\) in Equation (28), it can be shown that
The time step required for numerical stability is \(\Delta t < 2 \eta / \alpha K\).
Implicit Algorithm
If \(\sigma=\sigma^{n+1}\) in Equation (28), it can be shown that
This algorithm is unconditionally stable. Even if \(\Delta t \to +\infty\), \(\sigma^{n+1}\) is still convergent to a bounded value \(\eta \dot{\varepsilon}\). Thus, the time step for integration of the Maxwell component does not have to be smaller than the time step used for the element dynamic integration. The implicit algorithm, Equation (30), is used for the FLAC3D implementation (Dawson and Cheng, 2021). For solid elements, the actual implementation considers as a stress tensor, as a strain tensor and K as a constitutive stiffness matrix. For structural elements K is the element stiffness matrix.
Example Application of Maxwell Damping
The following example demonstrates how Maxwell damping works in FLAC3D.
Hysteretic Damping
The equivalent-linear method has been in use for many years to calculate the wave propagation (and response spectra) in soil and rock at sites subjected to seismic excitation. The method does not directly capture any nonlinear effects because it assumes linearity during the solution process; strain-dependent modulus and damping functions are only taken into account in an average sense in order to approximate some effects of nonlinearity (damping and material softening). Although fully nonlinear codes such as FLAC3D are capable—in principle—of modeling the correct physics, it has been difficult to convince designers and licensing authorities to accept fully nonlinear simulations. One reason is that the constitutive models available to FLAC3D are either too simple (e.g., an elastic/plastic model, which does not reproduce the continuous yielding seen in soils), or too complicated (e.g., the Wang model [Wang et al. 2001], which needs many parameters and a lengthy calibration process). Further, there is a need to directly accept the same degradation curves used by equivalent-linear methods (see Figure 9 and 10 for examples), to allow engineers to move easily from using these methods to using fully nonlinear methods.
A further motivation for incorporating such cyclic data into a hysteretic damping model for FLAC3D is that the need for additional damping such as Rayleigh damping would be eliminated. Rayleigh damping is unpopular with code users because it often involves a drastic reduction in timestep, and a consequent increase in solution time.
Optional hysteretic damping is described here; it may be used on its own or in conjunction with the other damping schemes, such as Rayleigh damping or local damping. (It may also be used with some of the built-in constitutive models except for the models with nonlinear elastic moduli, e.g., modified Cam-Clay.)
The hysteretic damping formulation is not intended to be a complete constitutive model: it should be used as a supplement to one of the built-in nonlinear models, and not as a primary way to simulate yielding. If models that embody both plastic yield and an adequate hysteretic response are used, then there is no reason to add further damping; the hysteretic damping option in FLAC3D is only intended to provide damping for those models lacking intrinsic damping when not yielding. Further, Rayleigh damping should be unnecessary when hysteretic damping is in operation, apart from its possible use (at low levels: e.g., 0.2%) to remove high frequency noise.
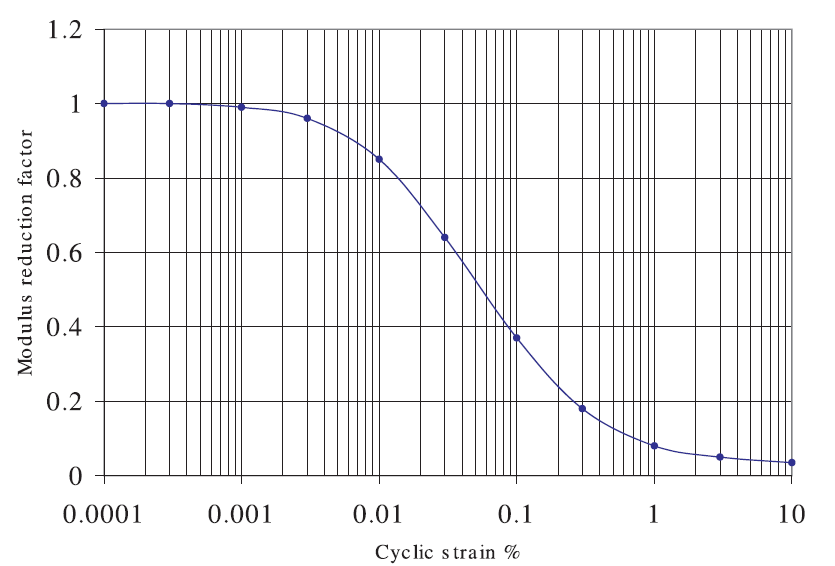
Figure 9: Modulus reduction curve for sand (Seed & Idriss 1970 — “upper range”). The data set is from the file supplied with the SHAKE-91 code download.(https://nisee.berkeley.edu/elibrary/getpkg?id=SHAKE91)
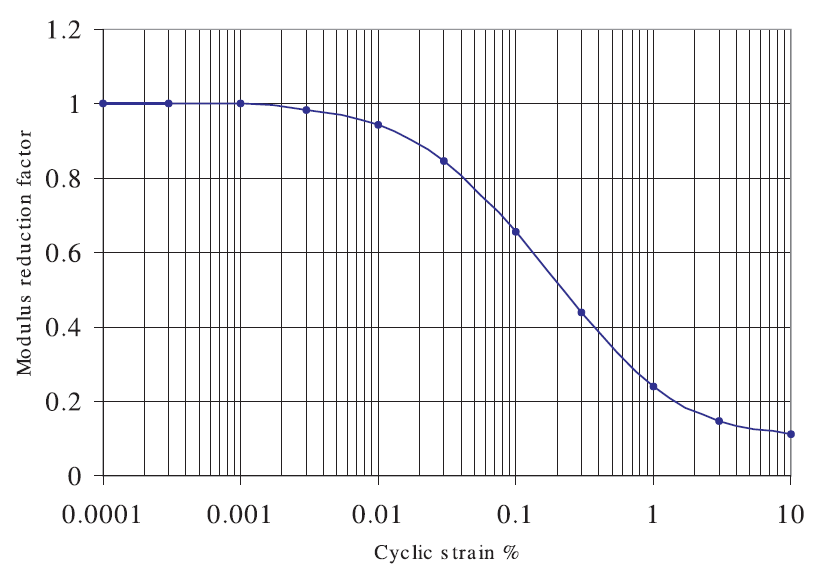
Figure 10: Modulus reduction curve for clay (Sun et al. 1988 — “upper range”). The data set is from the file supplied with the SHAKE-91 code download. (https://nisee.berkeley.edu/elibrary/getpkg?id=SHAKE91)
Formulation
Modulus degradation curves, as illustrated in Figures 9 and 10, imply a nonlinear stress/strain curve. If we assume an ideal soil, in which the stress depends only on the strain (not on the number of cycles, or time), we can derive an incremental constitutive relation from the degradation curve, described by \(\bar {\tau} / \gamma = M_s\), where \(\bar {\tau}\) is the normalized shear stress, \(\gamma\) is the shear strain, and \(M_s\) is the normalized secant modulus.
where \(M_t\) is the normalized tangent modulus. The incremental shear modulus in a nonlinear simulation is then given by \(G_o M_t\). This is used in place of the given shear modulus, \(G_o\) (i.e., the property assigned with the name shear).
In order to handle two- and three-dimensional strain paths, an approach similar to the one described for the Finn model (see Simple Model Formulations) is used, whereby the shear strain is decomposed into components in strain space, and strain reversals are detected by changes in signs of the dot product of the current increment and the previous mean path. Following the formulation of the Finn model (replacing \(\epsilon\) with \(\gamma\) but otherwise using the same notation):
A reversal is detected when \(|d|\) passes through a maximum, and the previous-reversal strain values are updated as given by Equations (43) and (44). Note that there is no “latency” period, as used in the Finn model (see Simple Model Formulations); there is no minimum number of timesteps that must occur before a reversal is detected.
Between reversals, the shear modulus is multiplied by \(M_t\), using \(\gamma = |d|\) in Equation (32). The multiplier is applied to the shear modulus used in all built-in constitutive models, except for the transversely isotropic elastic, modified Cam-clay, and creep material models.
Implementation
The formulation described above is implemented in FLAC3D, by modifying the strain-rate calculation so that the mean strain-rate tensor (averaged over all subzones) is calculated before any calls are made to constitutive model functions. At this stage, the hysteretic logic is invoked, returning a modulus multiplier, which is passed to any called constitutive model. The model then uses the multiplier \(M_t\) to adjust the apparent value of tangent shear modulus of the full zone being processed.
In addition to the “backbone curve,’’ provided by applying Equation (32) to a modulus degradation curve (described below), two Masing (1926) rules are used to specify the behavior at reversal points. Essentially, these state that: 1) a new (but inverted) function is started upon reversal, implying that the initial unload modulus is \(G\); and 2) the first quarter-cycle of loading is scaled by one-half relative to all other cycles. Although Pyke (2004) concludes that “neither of the Masing rules is valid,” some simplifying assumption is necessary to ensure repeatable, closed loops. The fact that real soil departs from this ideal behavior is not believed to be too important in this context because the formulation is not intended to be a complete constitutive model, but simply to provide hysteretic damping as an alternative to Rayleigh damping.
An additional rule deals with sub-cycles: the hysteretic logic contains push-down FILO (first in, last out) stacks that record all state information (e.g., stress, strain, tangent modulus, and previous reversal point) at the point of reversal, for both positive—and negative—going strain directions. If the strain level returns to—and exceeds—a previous value recorded in the stack (of the appropriate sign), the state information is popped from the stack, so that the behavior (and, hence, tangent multiplier) reverts back to that which was applied at the time before the reversal.
The operation of these various rules in illustrated in the following simple example:
The degradation curves used in earthquake engineering are usually given as tables of values, with cyclic strains spaced logarithmically. Since the derivative of the modulus-reduction curve is required here (i.e., for Equation (32)), the coarse spacing (e.g., 11 points in the curve shown in Figure 10) leads to unacceptable errors if numerical derivatives are calculated. Thus, the implemented hysteretic model uses only continuous functions to represent the modulus-reduction curve, so that analytical derivatives may be calculated. The various implemented functions are described in the following section. If degradation curves are available only in table form, they must be fitted to one of the built-in functional forms before simulations can be performed.
The hysteretic damping feature is invoked with the command
zone dynamic damping hysteretic name <v1 v2 v3 …> <range>
where name is the name of the fitting function (chosen from default, sigmoidal-3, sigmoidal-4, and hardin — see the following discussion), and v1, v2, v3, …, are numerical values for function parameters. The optional range may be any acceptable range phrase for zones.
Hysteretic damping may be removed from any range of zones with the command
zone dynamic damping hysteretic off <range>
Note that the zone dynamic damping hysteretic command only applies where the model configure dynamic mode of operation has been selected and when model configure dynamic applies. Hysteretic damping operates independent of all other forms of damping, which may be also specified to operate “in parallel” with hysteretic damping.
Tangent-Modulus Functions
Various built-in functions are available to represent the variation of the shear modulus reduction factor, \(G/G_{\rm max}\), with cyclic strain (given in percent), according to the keyword specified on the zone dynamic damping hysteretic command.
Default model — default
The default hysteresis model is developed by noting that the S-shaped curve of modulus versus logarithm of cyclic strain can be represented by a cubic equation, with zero slope at both low strain and high strain. Thus, the secant modulus \(M_s\) is
where
and \(L\) is the logarithmic strain,
The parameters \(L_1\) and \(L_2\) are the extreme values of logarithmic strain (i.e., the values at which the tangent slope becomes zero). Thus, giving \(L_1 = -3\) and \(L_2 = 1\) means that the S-shaped curve will extend from a lower cyclic strain of 0.001% (10-3) to an upper cyclic strain of 10% (101). Since the slopes are zero at these limits, it is not meaningful to operate the damping model with strains outside the limits. (Note that Equation (45) is only assumed to apply for \(0 \leq s \leq 1\), and that the tangent modulus will be set to zero otherwise.) The tangent modulus is given by
Using the chain rule,
we obtain
There is a further limit, \(s > s_{\rm min}\), such that the tangent modulus is always positive (no strain softening). Thus,
or
where \(A = 6 {\rm log}_{10}e / (L_2 - L_1)\). The lowest positive root is
In applying the model, \(M_t = 0\) if \(s < s_{\rm min}\).
The default model function can be fit to degradation curves by using a curve-fitting graphing software (e.g., SigmaPlot, http://www.systat.com/products/sigmaplot/ ). For example, the numerical best-fit of the default model to the curves of Figures 9 and 10 are listed in Tables 2 and 3, respectively.
Sigmoidal models — sigmoidal-3, sigmoidal-4
Sigmoidal curves are monotonic within the defined range and have the appropriate asymptotic behavior. Thus the functions are well-suited to represent modulus degradation curves. The two types of sigmoidal model (3 and 4 parameters, respectively) are
sigmoidal-3 model
sigmoidal-4 model
The command line for invoking these models requires that three symbols, \(a\), \(b\), and \(x_o\), are defined by the parameters v1, v2, and v3, respectively, for model sig3 (Equation (54)). For model sigmoidal-4 (Equation (55)), the four symbols, \(a\), \(b\), \(x_o\), and \(y_o\), are entered by means of the parameters v1, v2, v3, and v4, respectively. Numerical fits for the two models to the curves of Figures 9 and 10 are provided in Tables 2 and 3, respectively.
Hardin/Drnevich model — hardin
The following function was suggested by Hardin and Drnevich (1972):
It has the useful property that the modulus reduction factor is 0.5 when \(\gamma = \gamma_{\rm ref}\), so that the sole parameter, \(\gamma_{\rm ref}\), may be determined (by inspection) from the strain at which the modulus-reduction curve crosses the \(G / G_{\rm max}\) = 0.5 line. Choosing a value of \(\gamma_{\rm ref}\) = 0.06 produces a match to the curve of Figure 9, and a value of 0.234 produces a match to the curve of Figure 10.
Using Masing rule, the damping of Hardin/Drnevich model can be calculated by
The maximum damping \(D_{max}\) is
This high maximum damping ratio does not match with the experiment data that is usually between 20~35%.
Ramberg-Osgood model — ramberg-osgood
The Ramberg-Osgood model suggests:
where \(\tau_{ref}\), \(r\) and \(\alpha\) are material constants.
Define \(\gamma_{ref} = \bar{\tau}_{ref}/G_o\), and note that that \(\bar{\tau} = G \gamma\) and \(M_s = G/G_o\), the Ramberg-Osgood model can be rewritten by
The required material constants thus become \(\gamma_{ref}\), \(r\) and \(\alpha\). It appears that different from other hysteretic models, the Ramberg-Osgood \(M_s\) cannot be directly expressed by a function of \(\gamma\). Instead, an iteration method can be used to solve \(M_s\) based on Equation (60).
Using Masing rule, the damping of Ramberg-Osgood model can be calculated by
The maximum damping \(D_{max}\) is
With the parameter \(r\), the Ramberg-Osgood model overcomes the shortcoming of Hardin/Drnevich model of overly high \(D_{max}\). The parameter \(r\) can be calibrated by
Apparently, a valid \(r\) should satisfy \(r>1\). For example, if \(D_{max}\) = 35%, \(r\) will be calibrated to 3.44.
Once \(r\) is determined, \(\alpha\) can be estimated from (60), e.g., when \(M_s = G/G_0\) = 0.5 at \(\gamma_{0.5}\), by
One of the drawback of the Ramberg-Osgood model is the fact that the shear strain increases in proportional to shear stress when the shear strain becomes large. In view of the possible range of the parameter \(r\) supposedly taking a value between 2 and 4, the quantity of shear stress tends to increase indefinitely with increasing shear strain, which is inconsistent with the real behavior of soils (Ishihara 1996). However, combining with the simple Mohr-Coulomb shear failure criteria, which assumes a limited ultimate shear stress when in shear yielding, will overcome this drawback.
Data set |
Default |
Sigmoidal-3 |
Sigmoidal-4 |
Hardin |
|---|---|---|---|---|
Sand–upper range |
\(L_1\) = -3.325 |
\(a\) = 1.014 |
\(a\) = 0.9762 |
\(\gamma_{\rm ref}\) = 0.060 |
(Seed &Idriss 1970) |
\(L_2\) = 0.823 |
\(b\) = -0.4792 |
\(b\) = -0.4393 |
|
\(x_o\) = -1.249 |
\(x_o\) = -1.285 |
|||
\(y_o\) = 0.03154 |
Data set |
Default |
Sig3 |
Sig4 |
Hardin |
|---|---|---|---|---|
Clay–upper range |
\(L_1\) = -3.156 |
\(a\) = 1.017 |
\(a\) = 0.922 |
\(\gamma_{\rm ref}\) = 0.234 |
(Sun at el. 1988) |
\(L_2\) = 1.904 |
\(b\) = -0.5870 |
\(b\) = -0.481 |
|
\(x_o\) = -0.633 |
\(x_o\) = -0.745 |
|||
\(y_o\) = 0.0823 |
Calibration of Degradation Curves
Calibration of the tangent-modulus function involves both a comparison of the function results to the target shear-modulus reduction curve and a comparison to the target damping-ratio curve. The following simple example is provided for illustration and discussion:
In most attempts to match laboratory and numerical damping curves, it is noted that the damping provided by the hysteretic formulation at low cyclic strain levels is lower than that observed in the laboratory. This may lead to low-level noise, particularly at high frequencies. Although such noise hardly affects the essential response of the systems, for cosmetic reasons it may be removed by adding a small amount of Rayleigh damping. It is found that 0.2% Rayleigh damping (at an appropriate center frequency) is usually sufficient to remove residual oscillations without affecting the solution timestep.
Simple Application
The example provided below models a 20 m layer excited by a digitized earthquake to show that plausible behavior occurs for a case involving wave propagation, multiple and nested loops, and reasonably large cyclic strain.
Observations
A method has been developed to use cyclic modulus-degradation data directly in a FLAC3D simulation. The resulting model is able to reproduce the results of constant-amplitude cyclic tests, but it is also able to accommodate strain paths that are arbitrary in strain space and time. Thus, it should be possible to make direct comparisons between calculations made with an equivalent-linear method and a fully nonlinear method, without making any compromises in the choice of constitutive model. The developed method is not designed to be a plausible soil model; rather, its purpose is to allow current users of equivalent-linear methods a painless way to upgrade to a fully nonlinear method. Further, the hysteretic damping of the new formulation will enable users to avoid the use of Rayleigh damping and its unpopular timestep penalties. A comparison of a layered model, assuming nonlinear elastic material using SHAKE, to one using FLAC3D with hysteretic damping is provided in Comparison of FLAC3D to SHAKE for a Layered, Nonlinear-Elastic Soil Deposit.
Practical Issues When Using Hysteretic Damping
The following conditions should be checked when hysteretic damping is applied in a dynamic simulation.
Compare hysteretic damping response to laboratory tests — It is generally not useful to compare apparent damping response from the hysteretic damping model used with a yield constitutive model to damping curves from laboratory results, because laboratory tests are likely to be unstable when shear failure occurs, and therefore unable to provide meaningful results. It is recommended that FLAC3D’s hysteretic response be matched to cyclic laboratory results obtained for a strain range that excludes failure, and that plasticity parameters (e.g., cohesion and friction angle) be matched to static laboratory strength tests. FLAC3D is able to combine the response in both regimes during a typical simulation of seismic response.
Check cyclic strain level — Hysteretic damping not only adds energy loss to dynamic straining, it also causes the mean shear modulus to decrease for large cyclic strains. This may lead to unexpected results (e.g., an increased response amplitude, due to the shift in resonance frequency closer to the dominant frequency of input waves).
Before running a dynamic model with hysteretic damping, an elastic simulation should be made without damping to observe the maximum levels of cyclic strain that occur. If the cyclic strains are large enough to cause excessive reductions in shear modulus for a given modulus reduction curve, then the use of hysteretic damping is questionable—it will be performing outside of its intended range of application. The model properties and input should be checked. If the properties and input are reasonable and the large cyclic strains are limited to small regions, then consider the possibility of excluding hysteretic damping from these regions and using only a yield model in these regions (because the large strains imply that yielding should occur).
Check modulus reduction factor — Even if cyclic strains under elastic conditions are small, the use of a yield model may increase the strains. The hysteretic damping formulation is not intended to be a substitute for a yielding constitutive model. It may be used in conjunction with a yield model (such as Mohr-Coulomb), but conflicts in the domain of application should be avoided if meaningful results are to be expected.
Hysteretic damping is “switched off” for each zone while plastic flow is occurring (including the associated strain accumulation for the hysteretic damping calculation). Note that the stiffness-proportional component of Rayleigh damping is also switched off during plastic flow.
Even so, the apparent modulus used by the hysteretic damping logic may drop to low values, which can cause unrealistic response. Low (or zero) values of the modulus can be checked by monitoring the modulus reduction factor, which is the factor by which the small-strain modulus, \(G_o\), is multiplied for hysteretic damping. (For example, use the FISH zone variable zone.hysteretic to access the factor for selected zones.)
In order to avoid the very low reduction factor which may cause unrealistic overly large deformation, a cut-off option can be set. The syntax to set this cut-off reduction factor is using the keyword “reduction-minimum” following by a user-defined value, i.e.,
zone dynamic damping hysteretic name <v1 v2 v3 v4> <reduction-minimum v5> <range>
In some simulations, large modulus reductions have been noticed in areas remote from regions of plastic flow (e.g., near the base of the model). It appears that the use of a single modulus-reduction curve is unrealistic in these cases. There is evidence (e.g., see Darendeli 2001) that degradation curves depend on the mean stress level: for example, at depth (high mean stress), there is less damping and modulus reduction. By making the hysteretic damping depth-dependent, the simulation should be more realistic.
Check initial shear stress state — In laboratory tests, the initial shear stress is assumed to be zero, leading to hysteresis loops that are generally symmetrical. In practical applications, the initial shear stress is unlikely to be zero (for example, within soil elements near the surface of an embankment). The user of hysteretic damping must decide on the best estimate of the initial state of the material, because the hysteretic formulation in FLAC3D depends on the past history of shear strain. Two cases can be identified:
If hysteretic damping is activated after a set of equilibrium stresses has been installed, then the initial shear strain will be zero, and cyclic excursions of shear stress will tend to be symmetrical about the starting point.
If the initial stresses are built up by straining the model while hysteretic damping is active, then subsequent cyclic excursions of shear stress will tend to be asymmetrical because the initial bias in strain causes the slope of the stress/strain curve to be flatter on the side with higher stress.
These cases are illustrated in the example One-Dimensional Earthquake Excitation of Uniform Layer by modifying the initial model into two further cases.
The approach of using a full static solution while hysteretic damping is active, in order to obtain a compatible starting state for both stress and strain, may be used for more complicated models, such as embankments in which the slope area contains initial shear stresses. One drawback of the approach is that the static solution may involve many diminishing cycles of oscillation as the state of equilibrium is approached. Although these cycles tend to be quite small (and hardly affect the desired stress state), they cause many states to be stored on the memory stack (see Hysteretic Damping Formulation, Implementation and Calibration). These stored states are deleted from the stack early in dynamic loading, but they occupy memory and entail some initial overhead in computer time. It may be possible (in a future version of FLAC3D) to include logic to allow users to flush the stacks at the end of the static initialization, while retaining the latest state of stress-compatible strains for a dynamic simulation with hysteretic damping.
Local Damping
Local damping (see Mechanical Damping) was originally designed as a means to equilibrate static simulations. However, it has some characteristics that make it attractive for dynamic simulations. It operates by adding or subtracting mass from a gridpoint or structural node at certain times during a cycle of oscillation; there is overall conservation of mass, because the amount added is equal to the amount subtracted. Mass is added when the velocity changes sign and subtracted when it passes a maximum or minimum point. Hence, increments of kinetic energy are removed twice per oscillation cycle (at the velocity extremes). The amount of energy removed, \(\Delta W\), is proportional to the maximum, transient strain energy, \(W\), and the ratio, \(\Delta W/W\), is independent of rate and frequency. Since \(\Delta W/W\) may be related to fraction of critical damping, \(D\) (Kolsky 1963), we obtain the expression
where \(\alpha_{\rm L}\) is the local damping coefficient. Thus, the use of local damping is simpler than Rayleigh damping, because we do not need to specify a frequency. The example Block Under Gravity compares local damping to the other options.
A modified form of local damping—combined damping—may also be used in dynamic mode, but its performance is unknown. The formulation for combined damping is given in Mechanical Damping, and the command to invoke it is
zone.dynamic.damping.combined <v1>
CAUTION: Local damping appears to give good results for a simple case because it is frequency-independent and needs no estimate of the natural frequency of the system being modeled. However, this type of damping should be treated with caution, and the results compared to those with Rayleigh damping for each application. There is some evidence to suggest that, for complicated waveforms, local damping underdamps the high frequency components, and may introduce high frequency “noise.” Also note that local damping is timestep-dependent. Reducing the timestep will reduce the amount of energy removed from the system.
Local damping is not recommended for seismic simulations, because this type of damping cannot completely represent the energy loss of multiple cyclic loading properly.
Artificial Viscosity
von Neumann and Landshoff artificial viscosity terms are implemented in FLAC3D to control damping in dynamic analysis involving waveforms with rapid rise-times, such as shock waves. These viscous damping terms are a generalization of the one-dimensional equations (1) and (3) in Wilkins (1980) and correspond to the original viscosity formulation of von Neumann and Richtmyer (see Wilkins 1980).
The artificial viscosity method was initially developed for numerical calculation of shock propagation in fluid dynamics. The method may not apply to elastic or plastic waves when shear stress components are significant when compared to mean pressure, because shear waves are not damped by the method. The purpose of the quadratic von Neumann term \(q_1\) is to spread the shock over a number of grid spacings, and damp the oscillations behind the front. The effect of the linear Landshoff term \(q_2\) is to diffuse the shock front over an increased number of zones as the shock progresses.
In the FLAC3D implementation, a linear combination, \(q\), of the scalar viscosity terms \(q_1\) and \(q_2\) is used on a zone basis:
where \(a_n\) and \(a_l\) are two constants. The viscous terms have the form
where: |
\(L\) |
is a characteristic zone dimension (square root of the zone area); |
\(\dot\epsilon\) |
is the zone volumetric strain rate; |
|
\(\rho\) |
is the zone density; |
|
\(a\) |
is the material \(p\)-wave speed: \(a = {\sqrt{{(K + 4G/3) / \rho}}}\), where \(K\) and \(G\) are bulk and shear moduli for the zone; |
|
\(c_0\) |
is a constant set = 2; and |
|
\(c_1\) |
is a constant set = 1. |
and, to accommodate both compressive and dilatant shocks, we specify
The isotropic viscous stress contribution is added to the out-of-balance force for the nodes before resolution of the equations of motion.
The following command is provided to activate artificial damping for a FLAC3D model:
zone dynamic damping artificial-viscosity \(a_n\) \(a_l\)
where \(a_n\) and \(a_l\) are the two constants defined above, which should, in most instances, be assigned the value of 1.
Note that the presence of damping terms results in a slightly more stringent stability condition, which has not been taken into consideration in the implementation. Hence, in some cases, it may be necessary to reduce the timestep to achieve satisfactory numerical stability.
The example provided below illustrates the effects of artificial viscosity on an expansion wave with a sharp front propagating through a column of zones.
Integration of Damping Schemes and Nonlinear Material Models for Geo-materials
Energy dissipation in soil and rock is largely hysteretic in nature; the specific loss for each load/unload cycle of shear strain is independent of the rate at which the cycle is executed, but dependent on the amplitude of the cycle. Ideally, this behavior would be reproduced by an appropriate constitutive model, but adequate nonlinear models tend to be complicated, embodying many material parameters. Simpler models such as Mohr Coulomb are often used instead in order to reproduce irreversible strain accumulation (e.g., slumping or slip on shear surfaces) that may occur during seismic loading. In such models, additional damping must be included to account for cyclic dissipation during the elastic part of the response and during wave propagation through the site. Rayleigh damping is commonly used, but it only provides (approximately) rate-independent damping over a limited frequency range, and it entails a large reduction in critical timestep and consequent long runtimes.
The following discussion illustrates the ways damping can be integrated with a simple material model. We consider the use of hysteretic damping plus damping arising from plastic flow. Hysteretic damping is based on a secant modulus-reduction curve for primary loading (the backbone curve) and a Masing rule assumption for unloading/reloading to provide energy dissipation. Hysteretic damping is applied in the elastic range only, and natural damping provided by the constitutive model operates in the plastic range. Three simple cases are presented. First, the energy dissipation provided by a standard elastic/plastic Mohr-Coulomb is shown. Second, damping is incorporated into a linearly elastic model using hysteretic (Hardin/Drnevich model) damping. And third, the Hardin/Drnevich model is combined with the Mohr-Coulomb model. The energy dissipation is compared for all three cases by evaluating the change in shear modulus and damping ratio for each case.
Natural Damping with the Mohr-Coulomb Model
Standard elastic/plastic models such as Mohr-Coulomb can produce shear-modulus reduction and damping ratio curves. Consider an elastic/plastic model with a constant shear modulus, \(G_{max}\), and a constant yield stress, \(\tau_m\), subject to cyclic shear strain of amplitude \(|\gamma|\). Below yield, the secant shear modulus, \(G\), is simply equal to \(G_{max}\). For cyclic excitation that involves yield, the secant modulus is
The modulus-reduction curve relates the ratio \(G/G_{max}\) to the amplitude of shear strain, \(|\gamma|\); it is simply obtained by dividing Equation (70) by \(G_{max}\), and using \(\gamma_m\) = \(\tau_m\)/\(G_{max}\), we obtain, for \(|\gamma| > \gamma_m\),
A stress-strain cycle of amplitude \(\gamma_c\) > \(\gamma_m\), consisting of initial loading plus an unloading/reloading excursion, is sketched in Figure 11:
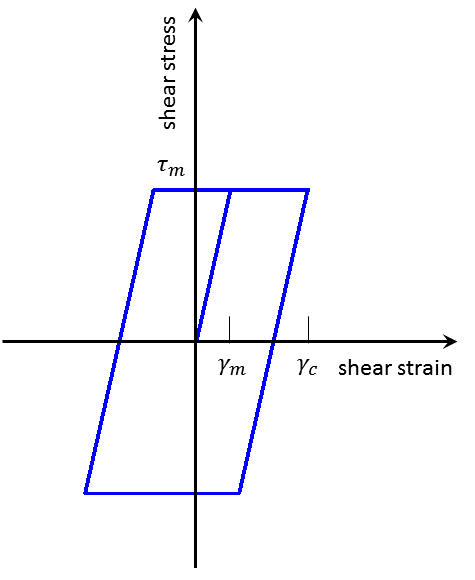
Figure 11: Shear stress/strain cycle—Mohr-Coulomb model.
The maximum stored energy, \(W\), during the cycle (assuming \(G\) represents an elastic modulus) is
and the dissipated energy (corresponding to the area enclosed by the loop) is
Hence,
Denoting the damping ratio by \(D\), and noting that for small values of \(D\) (Kolsky 1963),
or, substituting Equations (72) and (73) into Equation (75),
We plot normalized modulus (\(G/G_{max}\)) from Equation (71), and damping, \(D\), from Equation (73) against normalized cyclic strain, \(\gamma/\gamma_m\), in Equation (76). It can be seen that even a simple model (where “simple” is taken in the context of dynamics) exhibits an evolution of modulus and damping that can be matched to experimental results over limited ranges of cyclic strain.
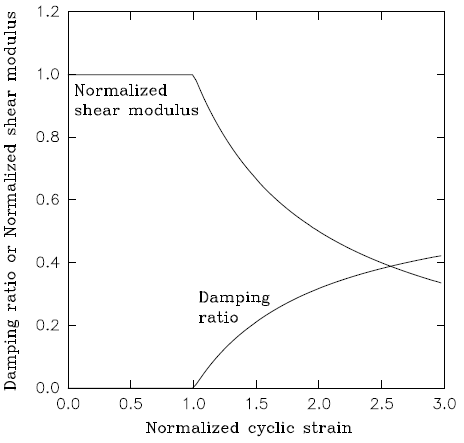
Figure 12: Modulus and damping ratio versus cyclic strain for elastic/plastic Mohr-Coulomb model.
Hysteretic Damping with the Linear Elastic Model
For the hysteretic damping model using the Hardin/Drnevich function described in Hysteretic Damping Formulation, Implementation, and Calibration, the backbone curve is given by
where \(\gamma_{ref}\) is the constant for the Hardin/Drnevich function. \(\gamma_{ref}\) is the ultimate value of \(\tau/G_{max}\):
This curve is followed for primary loading. For unloading/reloading, the Masing rule holds. For the case of cyclic shear loading at constant amplitude, \(\gamma_c\), the Masing rule gives, for unloading,
and for reloading,
where
The initial loading curve and loop traced in one cycle of unloading/reloading is sketched in Figure 13.
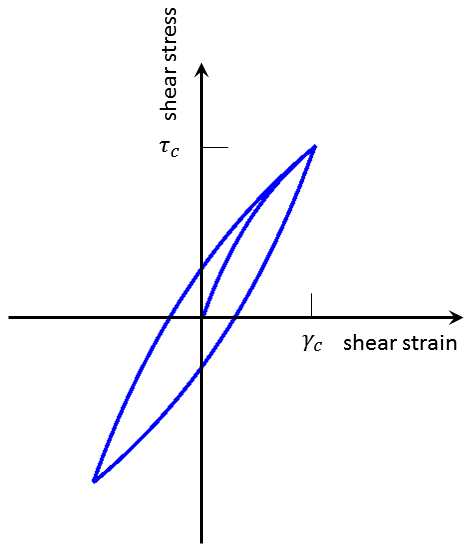
Figure 13: Shear stress/strain cycle—elastic model with Hardin/Drnevich hysteretic damping.
The energy dissipated in one full unloading-reloading cycle is given by the integral
After introduction of Equations (79) and (80) in Equation (82), and performing the integration, we obtain
The maximum stored energy in a cycle is
where \(\tau_c\) is given by Equation (81).
The damping ratio, \(D\), is obtained by combining Equations (82) and (83) with Equation (84):
Also, we note that application of l’Hospital rule gives
It is interesting to note that for the Hardin/Drnevich hysteretic damping and the elastic model, the damping ratio does not depend on \(G_{max}\). Also, \(D\) is larger for smaller values of \(\gamma_{ref}\). For an elastic, cyclic shear test of constant amplitude at constant volume, the use of hysteretic damping produces a response that is independent of the number of cycles performed.
Hysteretic Damping with the Mohr-Coulomb Model
When hysteretic damping is used with an elastic/plastic model in FLAC3D, the modulus-reduction technique is applied in the elastic range, and natural damping applies in the plastic range. In this case, we combine the Hardin/Drnevich hysteretic damping with a Mohr-Coulomb model. The Mohr-Coulomb model has a constant, tangent, elastic shear modulus, \(G_{max}\), and a constant yield stress, \(\tau_m\). The Hardin/Drnevich model is used to provide energy dissipation in the elastic range (but not to simulate yielding by means of a hyperbolic plasticity model). Accordingly, the yield level from the hyperbolic law must be higher than the Mohr-Coulomb yield stress. This will be the case provided that the following requirement is met:
where
An initial loading curve involving Mohr-Coulomb yielding and a loop traced in one cycle of unloading/reloading are sketched in Figure 14.
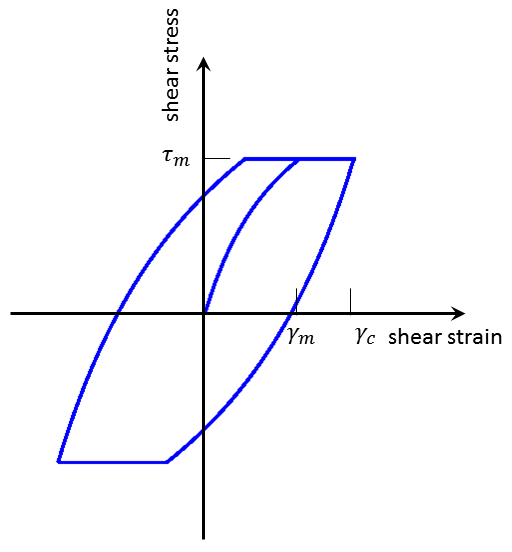
Figure 14: Shear stress/strain cycle—Mohr-Coulomb model with Hardin/Drnevich hysteretic damping.
The elastic range is defined by \(\gamma_c < \gamma_m\), where the shear strain, \(\gamma_m\), is found from the following relation (see Equation (77)):
In the elastic range, \(\gamma_c < \gamma_m\), the modulus reduction factor is given by Equation (77), or
In the plastic range, \(\gamma_c \ge \gamma_m\), the relation is
Also, in the plastic range, the energy dissipated in one cycle is the area enclosed by the loop in Equation (56). This energy may be expressed as the sum of two contributions:
where \(\Delta W_H\) is given by Equation (83)
and \(\Delta W_{MC}\) is expressed as (see Equation (73))
The maximum stored energy in one cycle is
and the damping ratio is
After substituting Equations (93) and (94) in Equation (96), we obtain with some manipulation,
The energy dissipation for the three damping cases is compared by exercising the equations for \(G/G_{max}\) and \(D\) over a cyclic strain range. A FISH function, listed in “datafiles\Dynamic\Damping-Compare\Damping-Compare.dat”, performs this exercise over a cyclic shear strain, \(\gamma_c\), from 0.0001 to 4.0. The value for \(\gamma_m\) is set to 0.01 and the value for \(\gamma_{ref}\) is set to 0.02. The results for \(G/G_{max}\) versus log \(\gamma_c/\gamma_m\), based upon Equations (71), (77), (90), and (91), are plotted in Figures 15. The results for \(D\) versus log \(\gamma_c/\gamma_m\), based upon Equations (76), (85), and (97), are plotted in Figure 16.
The inclusion of hysteretic damping is shown to reduce the shear modulus from the initial value of \(G_{max}\), and increase the damping ratio (compared to the elastic-only response). The damping ratio increases monotonically with shear strain amplitude and approaches the asymptotic value of \(2 / \pi\) for all three cases. To view this project, use the menu command .
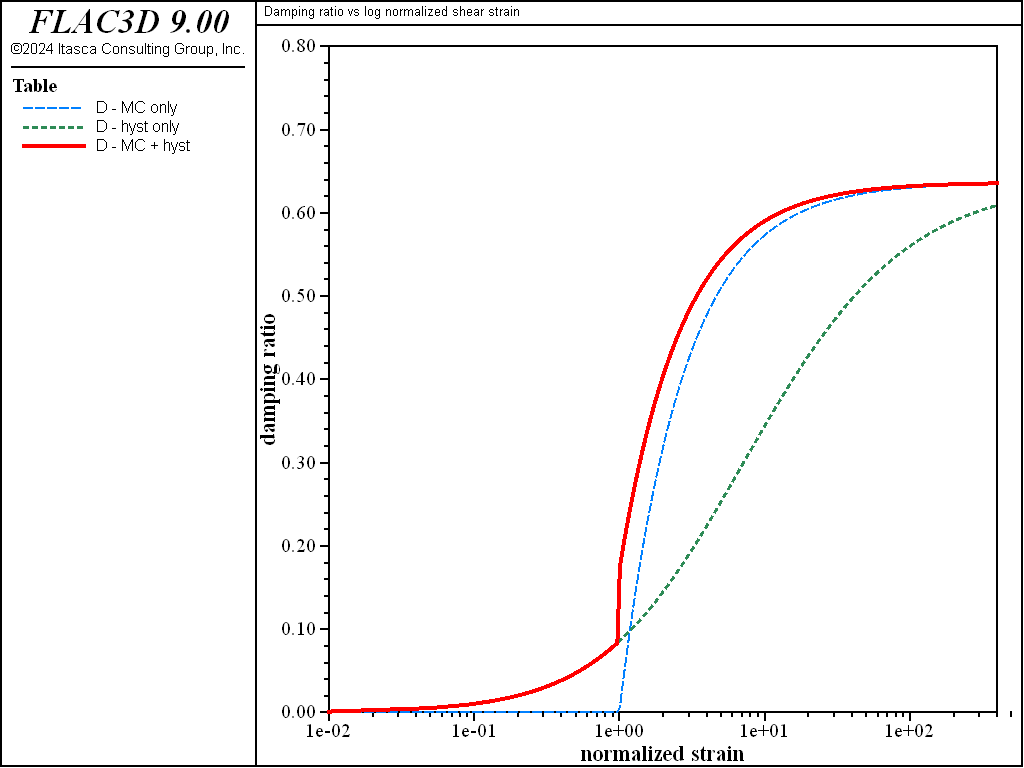
Figure 15: Normalized shear modulus vs log normalized shear stain for three damping cases.
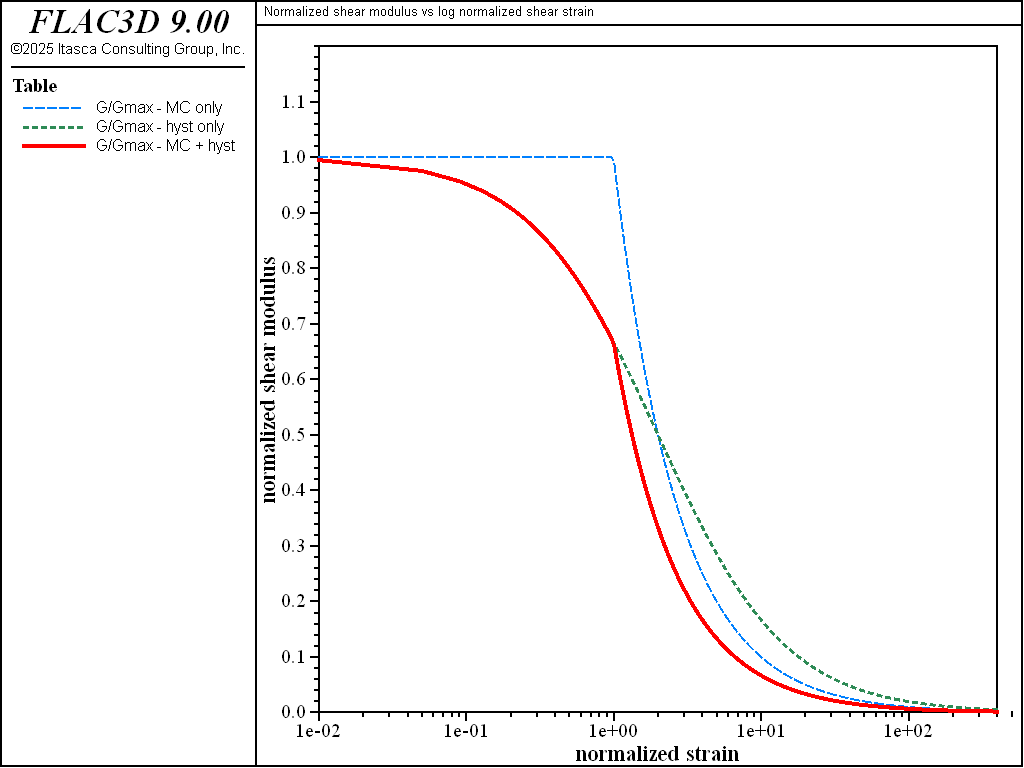
Figure 16: Damping ratio vs log normalized shear stain for three damping cases.
Spatial Variation in Damping
Rayleigh damping and local damping are both assigned via the zone dynamic damping command in FLAC3D. A spatial variation in the damping parameters (and the damping type) can be prescribed by including a range phrase to filter the gridpoints that are used for the command. For example, if different materials are known to have different fractions of critical damping, a different value of \(\xi_{\min}\) can be assigned to each material. This can be demonstrated by modifying the example of a wave propagating in a column. The following example is provided:
Nonuniform damping is specified by using a range in combination with the zone dynamic damping command. A gradient keyword may be used to vary damping constants in space. For example, we can modify the Raleigh damping parameters with the command:
zone dynamic damping rayleigh 0.05 gradient (0,0,-0.05) 25.0 gradient (0,0,-25)
In this case, there are spatial variations in both the damping coefficient and the center frequency. Note that all damping parameters pertain to gridpoints. In particular, the Rayleigh stiffness-proportional term, which acts on zone strain rates, is derived by averaging, from values specified at the neighboring gridpoints.
Structural Element Damping for Dynamic Simulations
Rayleigh, Maxwell, local, combined-local, and no damping can be specified independently for structural elements by giving the structure dynamic damping command. Damping is then applied for all structural elements in the model. The default damping for the structural elements in dynamic mode is no damping, and in static mode is local damping. Dynamic mode is activated with the model configure dynamic command, and general dynamic behavior is controlled with the model dynamic command. Additional information about structural-element damping is given here.
Structural-element damping and damping in the grid operate in similar ways. However, if a structural node is rigidly attached to a zone, the zone damping value is used instead of the structural node damping value. For the special case of a structural node attached to a null zone, the damping for that node is zero. The following example is provided:
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Nov 12, 2025 |
