Soft-Soil-Creep Model: Triaxial Consolidated Undrained Loading

Note

The project file for this example is available to be viewed/run in FLAC3D. The project’s main data files are shown at the end of this example.

This example is consolidated undrained triaxial loading with a constant rate of strain that corresponds to a maximum strain of 20% in 2160 minutes. The clay has an assumed initial isotropic (OCR = 1) effective stress of 10 kPa and an initial OCR of 6 (the pre-consolidation pressure is thus 60 kPa). A fixed creep time step of 0.216 min is used in this example. The input properties are listed in the below table:

\(\lambda^*\)	0.106
\(\kappa^*\)	0.016
\(v\)	0.25
\(\phi\)	30°
\(\mu^*\)	0.004
\(\tau\)	0.7 (min)
\(K_{nc}\)	0.62

The material properties are compatible with those given in the comparison reference (Stolle, Vermeer, & Bonnier, 1999).

The clay is assumed normally consolidated and with an initial consolidated stress of 100 kPa. The clay is then triaxially loaded under the undrained condition. An automatic creep time step control is used in the simulation as shown in the datafile.

The results simulated by FLAC3D are illustrated in Figure 1 and Figure 2, which are matching very well as those in the comparison reference which used the finite element framework. As observed and expected, the deviatoric shear stress (q) increases and the effective mean pressure (p) decreases steadily until the Mohr-Coulomb shear failure line is reached. After this reach, the stress path moves downward along the Mohr-Coulomb shear failure line due to the creep-induced contraction, portraying the strain softening in the q vs. strain curve in Figure 1. It is noted that the simulation by FLAC3D shows very smooth curves even at the beginning of the loading.

Reference

Stolle, D. F., Vermeer, P. A., & Bonnier, P. G. “Time integration of a constitutive law for soft clays,” Communications in Numerical Methods in Engineering, 15(8), 603-609 (1999).

break

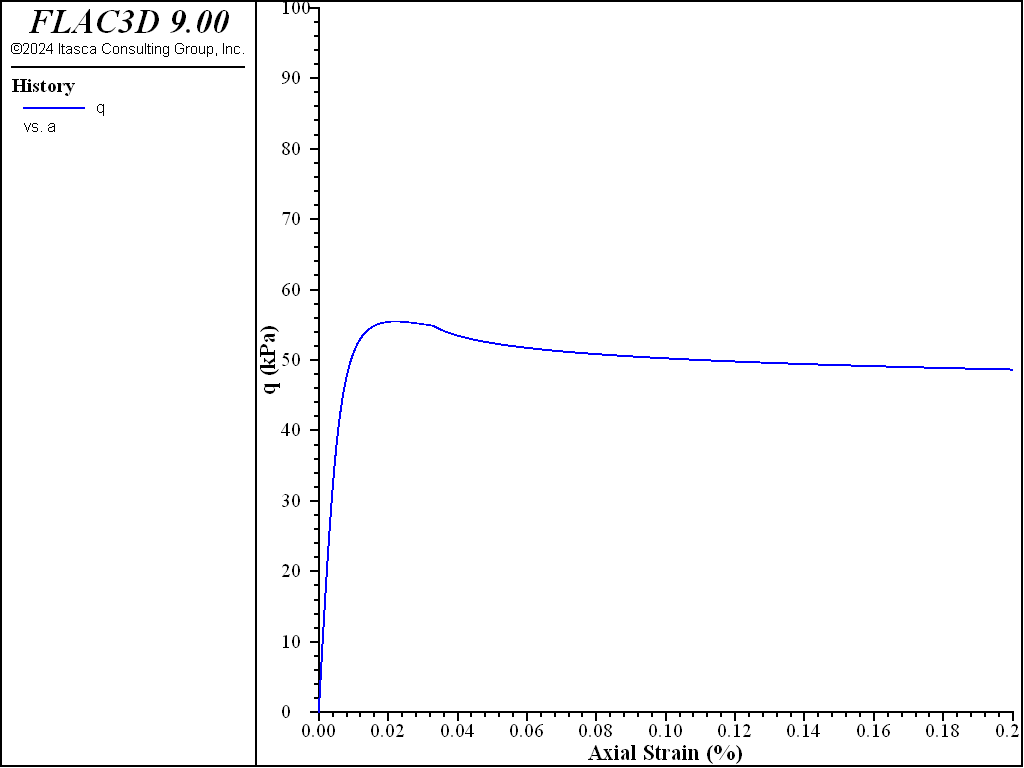
Figure 1: q vs. vertical strain.

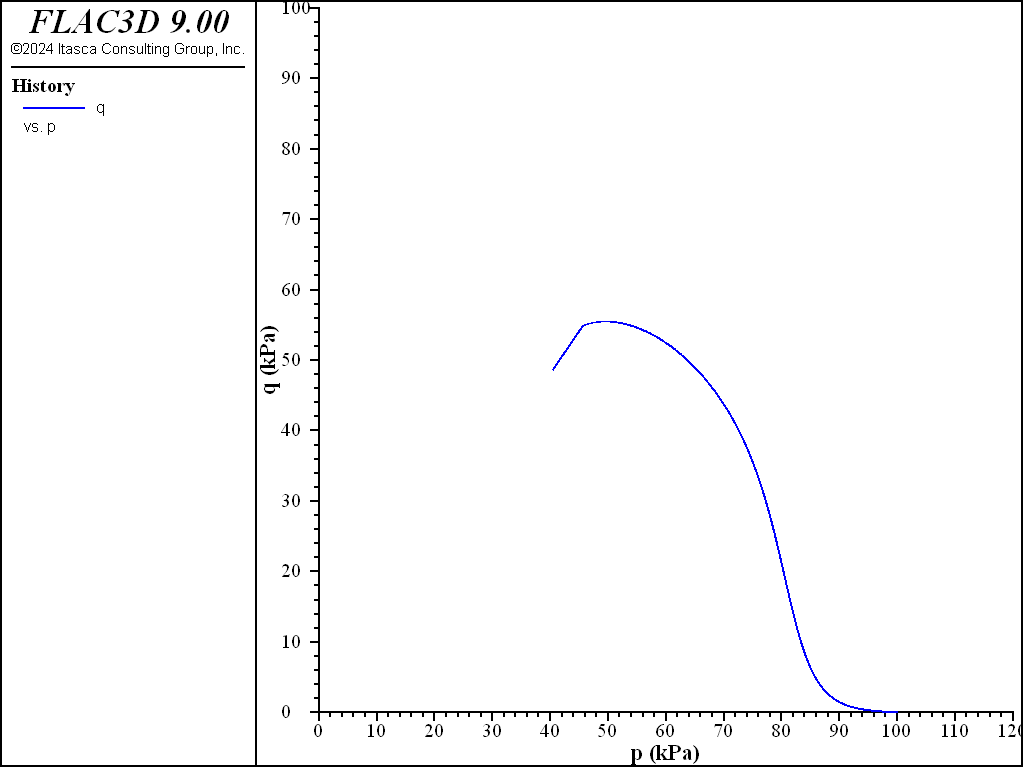
Figure 2: q vs. p.

Data File

model new
model large-strain off
model configure creep
;
[global cs0  = -100.0]
[global rate = 0.2/2160.0]
[global loadtime = 2160.0]
;
zone create brick size 1 1 1
zone face skin
zone cmodel assign soft-soil-creep
zone property lambda-modified 0.106 kappa-modified 0.016 poisson 0.25
zone property coefficient-normally-consolidation 0.62 ...
              over-consolidation-ratio 1.0
zone property friction=30.0 cohesion 0 dilation 0
zone property time-reference 0.7 index-creep 0.004
zone property stress-1-effective=[cs0] stress-2-effective=[cs0] ...
              stress-3-effective=[cs0]
;
zone face apply velocity-x=0.0 range group 'west'
zone face apply velocity-y=0.0 range group 'south'
zone face apply velocity-z=0.0 range group 'bottom'
zone initialize stress xx [cs0] yy [cs0] zz [cs0]

;
[global zp = zone.head]
[global gp = gp.find(8)]
fish define q_
    global q_ = zone.stress.xx(zp) - zone.stress.zz(zp)
    global a_ = -gp.disp.z(gp)
    global p_ = -(zone.stress.xx(zp) + zone.stress.yy(zp) + ...
                 zone.stress.zz(zp))/3.0
end
;
model history name 'time' creep time-total
fish history name 'q' q_
fish history name 'a' a_
fish history name 'p' p_
;
zone face apply velocity-z [-rate] range group 'top'
zone face apply velocity-x [0.5*rate] range group 'east'
zone face apply velocity-y [0.5*rate] range group 'north'
;
model creep timestep automatic on 
model creep timestep starting 1e-10 maximum 0.1 latency 10
model solve creep time-total [loadtime]
;
model save 'triaxial_cu_ssc'