Conduction in a Hollow Cylinder

Note

The project file for this example is available to be viewed/run in FLAC3D. The project’s main data files are shown at the end of this example.

A hollow cylinder of infinite length is initially at a constant temperature of 0°C. The inner radius of the cylinder is exposed to a constant temperature of 100°C, and the outer radius is kept at 0°C. The problem is to determine the temperatures and thermally induced stresses in the cylinder when the equilibrium thermal state is reached.

Nowacki (1962) provides the solution to this problem in terms of the temperatures and radial, tangential, and axial stresses at the steady-state thermal state:

\[\begin{split}\begin{split} T(r) \over T_a\ &=\ {\ln(b/r) \over \ln(b/a)} \\ {\sigma_r(r) \over m G T_a}\ &=\ - \left[{\ln(b/r) \over \ln(b/a)} - {{(b/r)^2 - 1} \over {(b/a)^2 - 1}} \right] \\ {\sigma_t(r) \over m G T_a}\ &=\ - \left[{{\ln(b/r) - 1} \over \ln(b/a)} + {{(b/r)^2 + 1} \over {(b/a)^2 - 1}} \right] \\ {\sigma_a(r) \over m G T_a}\ &=\ - \left[{{2 \ln(b/r) - {\lambda \over 2 (\lambda + G)}} \over \ln(b/a)} + \left({\lambda \over 2 {\lambda + G}}\right) \left({2 \over (b/a)^2 - 1}\right) \right] \end{split}\end{split}\]

where:	\(T\)	=	temperature;
	\(r\)	=	radial distance from the cylinder center;
	\(a\)	=	inner radius of the cylinder;
	\(b\)	=	outer radius of the cylinder;
	\(T_a\)	=	temperature at the inner radius;
	\(\sigma_r\)	=	radial stress;
	\(\sigma_t\)	=	tangential stress;
	\(\sigma_a\)	=	axial stress;
	\(m\)	=	\(3 K \alpha_t \over {\lambda + 2 G}\);
	\(\lambda\)	=	\(K - {2 \over 3} G\);
	\(K\)	=	the bulk modulus;
	\(G\)	=	the shear modulus; and
	\(\alpha_t\)	=	the linear thermal-expansion coefficient.

The analytical solutions for temperature and stresses are programmed as FISH functions in the FLAC3D data file. The analytical and numerical results can then be compared directly in tables.

The following properties are prescribed for this example:

Geometry
inner radius of cylinder (\(a\))	1.0 m
outer radius of cylinder (\(b\))	2.0 m
Material Properties
density (\(\rho\))	2000 kg/m3
specific heat (\(C_p\))	880.0 J/kg °C
thermal conductivity (\(k\))	4.2 W/m °C
linear thermal-expansion coefficient (\(\alpha_t\))	5.4 × 10-6/ °C
shear modulus (\(G\))	28.0 GPa
bulk modulus (\(K\))	48.0 GPa

A thin quarter-section of the cylinder is modeled with FLAC3D. Figure 1 shows the FLAC3D grid. A constant-temperature boundary of 100°C is specified for the inner radius of the model; the temperature at the outer radius is specified to be 0°C.

The material in this problem is elastic. Therefore, an uncoupled analysis is appropriate. The thermal calculation is performed first to reach the equilibrium heat-flux state, then the thermally induced mechanical stresses are calculated.

Figure 1: FLAC3D grid for heating of a hollow cylinder.

Numerical and analytical results are compared in Figure 2 through Figure 5. The figures show plots of tables for temperature and stress distributions through the cylinder at steady state. In each figure, the analytical values are plotted as crosses, and the numerical values are plotted as dashed lines. The plotted values are normalized, with temperature normalized by dividing by \(T_a\) and stress normalized by dividing by \(m G T_a\). Figure 2 shows the temperature distribution at steady state for the numerical and analytical solutions. The agreement is very good, with an error of less than 0.1%. A comparison of results for radial, tangential, and axial stress distributions at steady state are provided in Figure 3, Figure 4, and Figure 5, respectively.

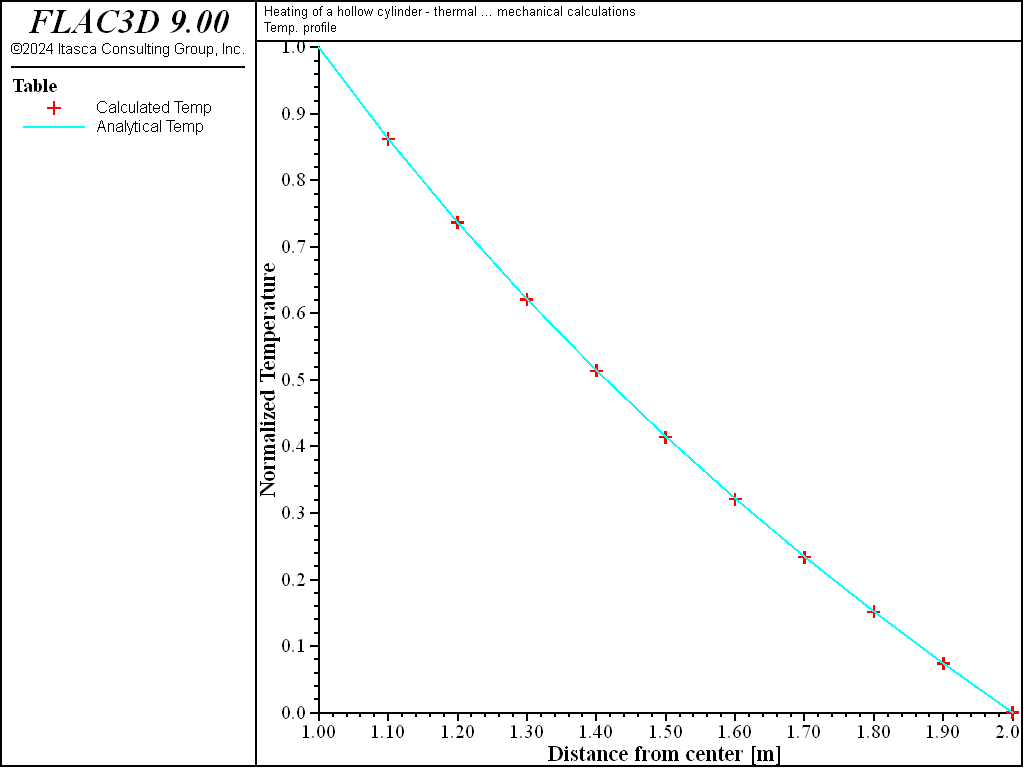
Figure 2: Temperature distribution at steady state for heating of a hollow cylinder.

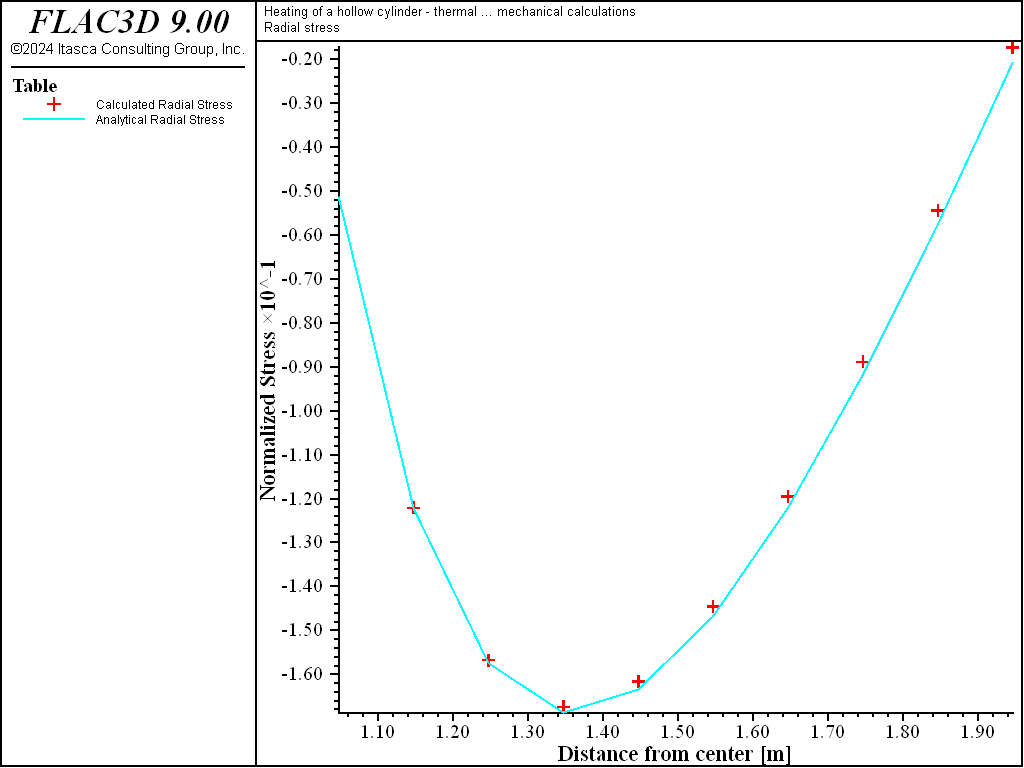
Figure 3: Radial stress distribution at steady state for heating of a hollow cylinder.

Figure 4: Tangential stress distribution at steady state for heating of a hollow cylinder.

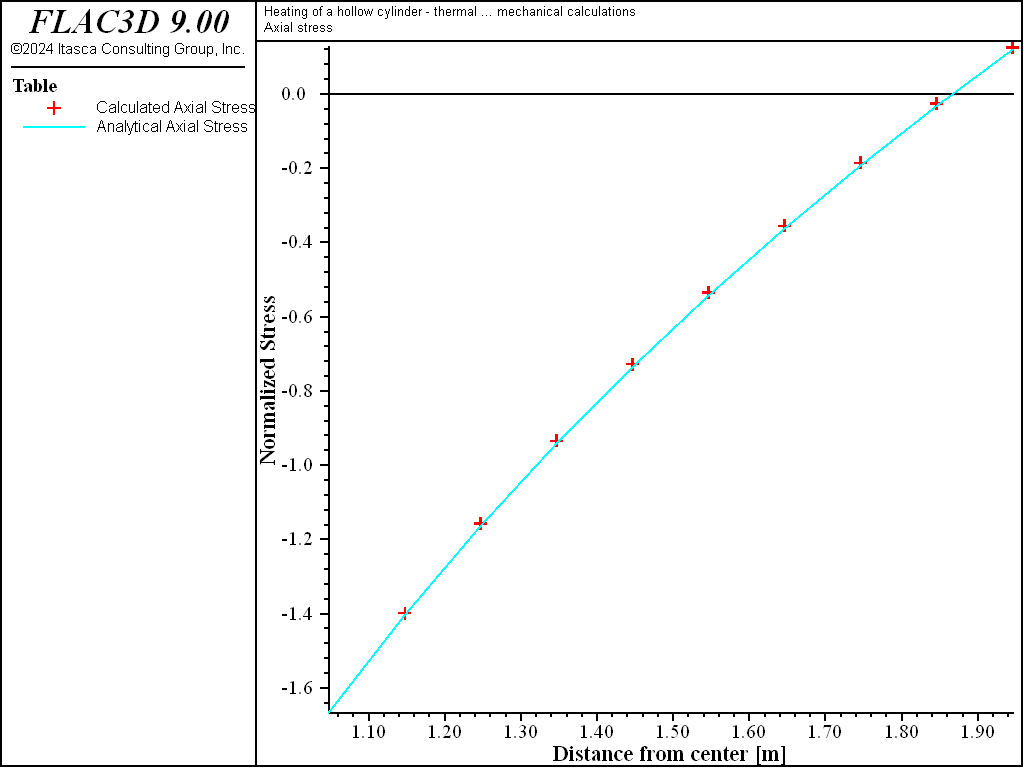
Figure 5: Axial stress distribution at steady state for heating of a hollow cylinder.

Reference

Nowacki, W. Thermoelasticity. New York: Addison-Wesley (1962).

Data File

; Heating of a hollow cylinder
; coupled and uncoupled thermal/mechanical calculations
model new
model large-strain off
fish automatic-create off
model title ...
      'Heating of a hollow cylinder - thermal ... mechanical calculations'
model configure thermal
; --- main computation ---
zone create cylindrical-shell point 1 (2,0,0) point 2 (0,0.1,0) ...
                              point 3 (0,0,2) dimension (1,1,1,1) size 10 1 12
zone face skin
; --- mechanical model
zone cmodel assign elastic
zone property bulk 48e9 shear 28e9
zone face apply velocity-z 0 range group 'Bottom'
zone face apply velocity-x 0 range group 'West1'
zone face apply velocity-y 0 range group 'North' or 'South'
; --- thermal model
zone thermal cmodel isotropic
zone thermal property conductivity 4.2 expansion 5.4e-6 specific-heat 880
zone initialize density 2000
zone face apply temperature 100 range group 'West2'
zone face apply temperature   0 range group 'East'
model save 'cyl-init'
;  uncoupled analysis
model mechanical active off 
model thermal active on
model solve
model mechanical active on 
model thermal active off
model solve
model thermal active on
model save 'cyl-ucpl'
;  coupled analysis
model restore 'cyl-init'
model mechanical active on
model thermal active on
model mechanical substep 10000 
model mechanical follower on
model solve thermal ratio 1e-5 mechanical convergence 1
model save 'cyl-cpl'
program return