Infinite Line Heat Source in an Infinite Medium

Note

To view this project in FLAC3D, use the menu command Help -> Examples…. The project’s main data files are shown at the end of this example.

An infinite line heat source with a constant heat-generating rate is located in an infinite elastic medium with constant thermal properties. Nowacki (1962) provides the solution to this problem for the transient values of temperature, radial and tangential stress, and radial displacement:

\[\begin{split}\begin{split} {{T}\over{a}}\ &=\ {1 \over {4 \pi}}\ E_1\ \left( \xi \right) \\ {{\sigma_r}\over{bG}}\ &=\ {1 \over {-4 \pi}}\ \left[ E_1 \left( \xi \right) + {{1 - e^{- \xi}} \over {\xi}} \right] \\ {{\sigma_t}\over{bG}}\ &=\ {1 \over {-4 \pi}}\ \left[ E_1 \left( \xi \right) - {{1 - e^{- \xi}} \over {\xi}} \right] \\ {{u_r}\over{bL}}\ &=\ {1 \over {8 \pi}}\ r \ \left[ E_1 \left( \xi \right) + {{1 - e^{- \xi}} \over {\xi}} \right] \end{split}\end{split}\]

where:	\(\xi\)	= \({r^2}\over{4 \kappa t}\);
	\(r\)	= radial distance to the line source;
	\(\kappa\)	= \({k \over {\rho C_p}}\);
	\(a\)	= \({q \over {k}}\);
	\(b\)	= \(\alpha_t \ a {9 K \over {3K + 4G}}\);
	\(L\)	= unit length;
	\(q\)	= energy uniform per unit length; and
	\(E_1(\xi)\)	= \(\int_{\xi}^\infty {e^{-u} \over {u}} du\) is the exponential integral.

The material properties and initial and boundary conditions for this example are defined as follows:

Material Properties
density (\(\rho\))	2000 kg/m3
specific heat (\(C_p\))	1000 J/kg °C
thermal conductivity (\(k\))	4 W/m °C
linear thermal-expansion coefficient (\(\alpha_t\))	5 × 10-6/ °C
shear modulus (\(G\))	30 GPa
bulk modulus (\(K\))	50 GPa
Initial/Boundary Conditions
initial uniform temperature	0°C
initial stress state	no stresses
Line Heat Source
energy release per unit length (\(q\))	1600 W/m

It is assumed that the material properties are temperature-independent, the thermal output of the source is constant (no decay), and the line heat source is of infinite length.

The FLAC3D grid for this problem is a quarter-section of a cylindrical disk. The axis of the line heat source coincides with the \(y\)-axis of the model. The grid is radially graded in the \(xz\)-plane; a single layer of zones is used in the \(y\)-direction. The model is shown in Figure 1.

Figure 1: FLAC3D grid for an infinite line heat source.

The line heat source is represented in FLAC3D by two point sources. The intensity of the point source \(q_p\) is adjusted to produce an energy release equivalent to that of a line source of linear intensity \(q\) into the model. For a quarter-symmetry model and two point sources on model thickness, \(t\), the relation between \(q_p\) and \(q\) is

(1)\[q_p\ =\ {q L \over 8}\]

The constant point heat source is applied at gridpoints along the \(y\)-axis; the boundaries of the model are kept adiabatic to represent thermal symmetry planes. The grid is extended to a distance of 500 m from the \(y\)-axis; this distance is chosen to be large enough to prevent boundary effects from affecting the solution up to the simulation target age of 1 year. The far boundary is mechanically fixed; the boundaries along the \(x\)-axis and \(z\)-axis are fixed to represent shear-free symmetry planes.

An uncoupled analysis is recommended because the material is elastic. The problem is first thermally solved to an age of one year (model mechanical active off and model thermal active on) using the implicit-solution algorithm, and then stepped to mechanical equilibrium (model mechanical active on and model thermal active off). For the mechanical phase, we use combined damping (zone mechanical damping combined). The heat source produces uniform motion in one direction for this problem. Combined damping is better suited to this case than local damping (see Mechanical Damping).

The dimensionless form of the analytical solutions in the equations above are programmed via FISH functions. The analytical and numerical values can then be compared directly in tables. The analytical solutions for temperature and radial displacement are programmed in the FISH function ana_soltu, and for radial and tangential stresses in ana_solst. The exponential integral function used in the analytical solutions is programmed as a separate FISH function called exp-int. The dimensionless values for the numerical results for temperature and displacement are calculated in the FISH function num_soltu, and for radial and tangential stresses in num_solst. The numerical values for dimensionless temperature, radial stress, tangential stress, and radial displacement are stored in Tables 1, 3, 5, and 7, respectively. The analytical values for dimensionless temperature, radial stress, tangential stress, and radial displacement are stored in Tables 2, 4, 6, and 8, respectively.

The results for temperature, radial displacement, and radial and tangential stress distributions at 1 year are presented in the table plots in Figure 2 to Figure 4. The difference between numerical and analytical solutions for temperature is less than 2%. The comparison is also good for displacements and for stresses; the difference is generally less than 2% within 100 m of the heat source. The fixed outer boundary has an influence on the numerical results farther from the source, but the agreement is still reasonable.

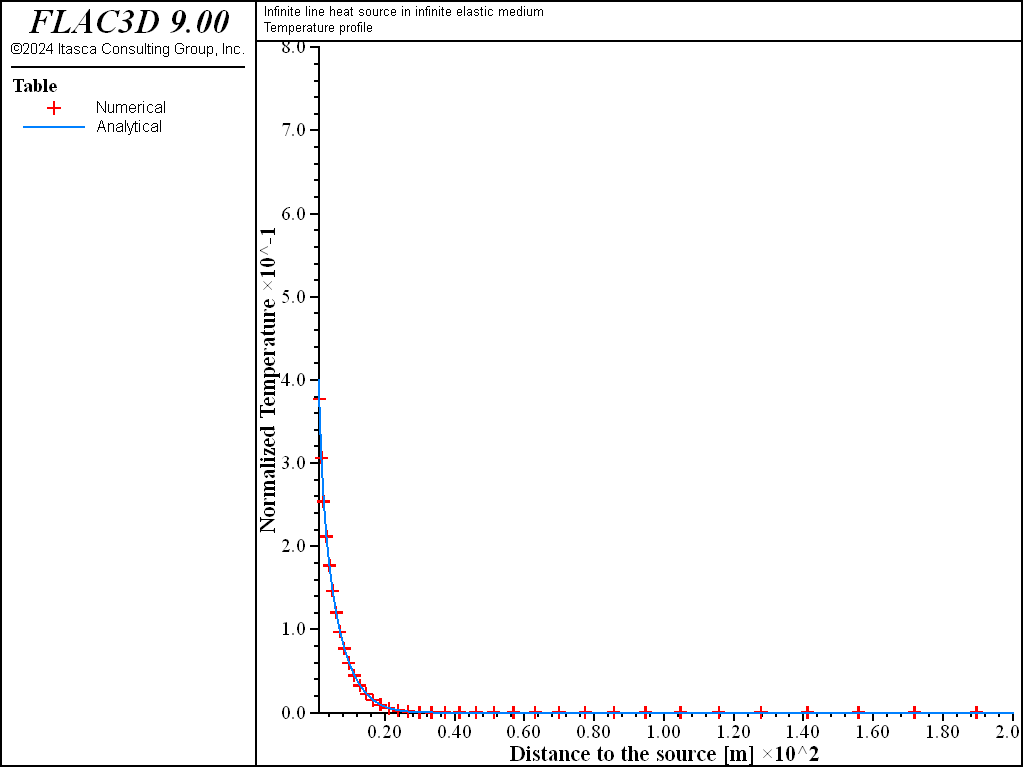
Figure 2: Temperature distribution at 1 year.

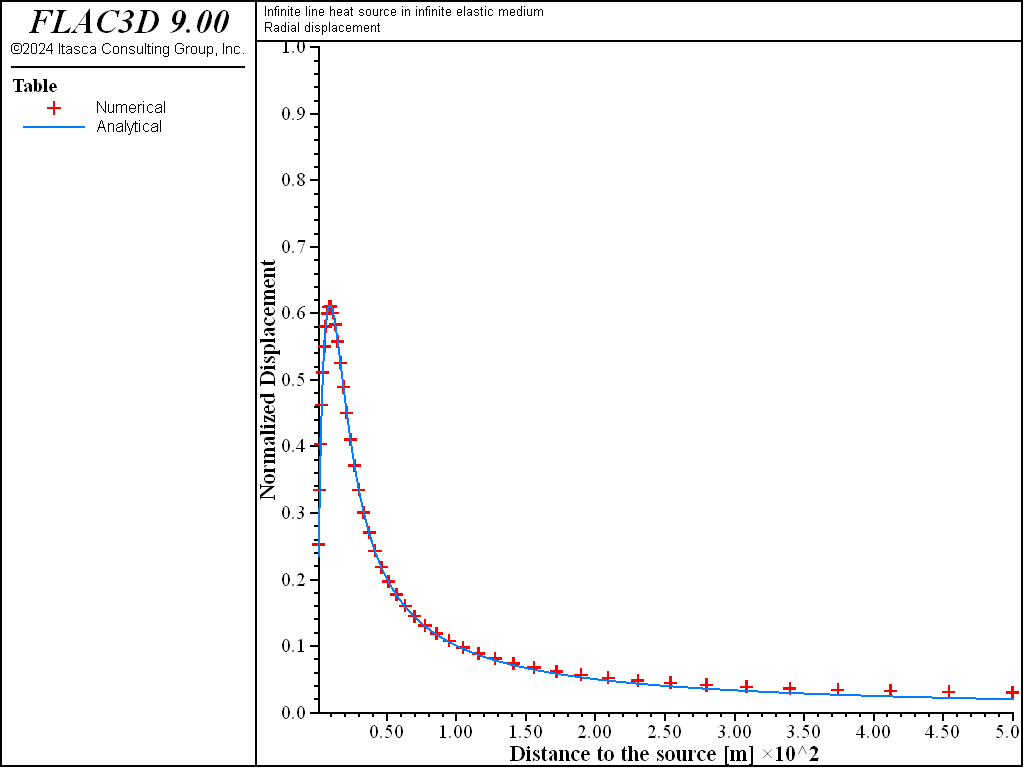
Figure 3: Radial displacement distribution at 1 year.

Figure 4: Radial and tangential stress distributions at 1 year.

Reference

Nowacki, W. Thermoelasticity. New York: Addison-Wesley (1962).

Data File

model new
model large-strain off
fish automatic-create off
model title 'Infinite line heat source in infinite elastic medium'
model configure thermal
;program call 'fishfunctions'
; --- model geometry
zone create cylinder point 1 (500,0,0) point 2 (0,1,0) point 3 (0,0,500) size (48,1,24) ratio (1.1,1,1)
zone face skin
zone face group 'Out' range group 'East'
; --- mechanical model
zone cmodel assign elastic
zone property density 2e3 bulk 5e10 shear 3e10
zone face apply velocity-x 0 range group 'West'
zone face apply velocity-y 0 range group 'North' or 'South'
zone face apply velocity-z 0 range group 'Bottom'
; --- thermal model
zone thermal cmodel isotropic
zone thermal property conductivity 4 expansion 5e-6 specific-heat 1e3
; --- line source
zone gridpoint fix source 200 range position-x 0 position-z 0
; --- settings
zone mechanical damping combined
zone thermal implicit on; solver-Jacobi

; use 3h timestep - this will cause Jacobi solver to fail after 6 steps and the system will switch to PCG solver
; PCG solver allows using much larger step but dt=3h is choosen to test the switch between solvers and accuracy
; previously, dt = 1.8h = 6.48e3sec and Jacobi solver works for this dt
model thermal timestep fix [3*60*60]

model save 'line-year0'
;  uncoupled analysis
model mechanical active off 
model thermal active on
model solve time-total [365*24*60*60]
model mechanical active on 
model thermal active off
model solve
model save 'line-year1-ucpl'