Axially Loaded Pile: End Bearing

Problem Statement

Note

The project file for this example is available to be viewed/run in FLAC2D. The main data files used are shown at the end of this example. The remaining data files can be found in the project.

EndBearing - One way to model end-bearing capactiy in FLAC2D is to neglect shear frction along the bottom segment of the pile, and instead adjust the properties of the corrsponding shear spring to account for the pile-bearing capacity. The approach of assigning a limit-load value on input is justified by considering that the indentation mechanism responsible for the limit load may not develop naturally in the approximate FLAC2D model adopted for the pile analysis (because the pile model does not account for cavity expansion).

In this example, the end-bearing spring is assigned a limit load, evaluated using an engineering bearing capacity formula (e.g., see [Coduto1994]). The limit load can also be derived from a cavity expansion theory (e.g., see [Bishop_et_al.1945], [Johnson1970], and [Teh_and_Houlsby1991] or from information derived from full-scale tests.

To illustrate the effect of end-bearing capacity, we first consider the case corresponding to a friction pile in sand (see the data file at the end of the example). The pile and grid geometries are similar to those in the Skin Friction example. Here the property \(c_s\) is set to zero and the pile friction (\(\phi_s\)) to 10 \(^{\circ}\), so that the pile shear strength is generated by confining pressure according to the shear behavior of the pile-grid boundary. A downward velocity is applied at the pile top, and the top force and vertical displacement are monitored for a total of 20,000 steps.

As may be observed from the pile top force-displacement history in Figure 1, the pile capacity has been reached by the end of the test. Figure 1 shows the distribution of shear forces in the shear coupling springs after 20,000 steps.

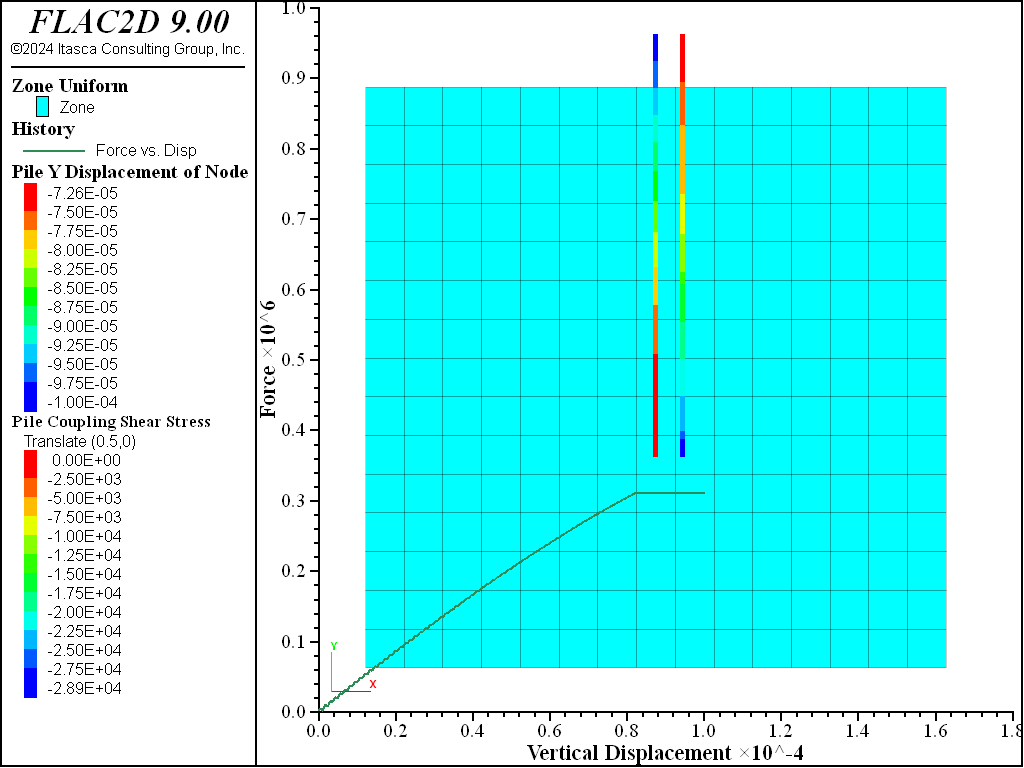
Figure 1: Friction pile: Top force-displacement history and shear stress along shaft.

The data file is than modified to simulate end bearing capacity. This is accomplished by assigning a limit-load capacity to the structural node at the base of the pile. The structural node at the pile base is the end-bearing node. The shear cohesion and shear stiffness of the coupling spring associated with the end node are adjusted to represent the effect of an end-bearing condition.

The stiffness, \(K_b\) of the bearing spring is adjusted to reflect the pile axial properties using

(1)\[K_b = {{EA} \over {L_e^2}}\]

where \(E\) is the pile elastic modulus, \(A\) is the cross-sectional area, and \(L_e\) is the effective length assigned internally to the bearing spring. The value of \(K_b\) (5.4 \(\times\) 10^11 N/m/m) is assigned via \(k_s\). Conceptually, the bearing spring acts as a pile extension, and the spring force may be interpreted as the axial force at the pile base.

The limit load, \(F_s^{max}\), in the bearing sping is evaluated from an engineering formula (e.g., see [Cernica1995]):

(2)\[F_s^{max} = A(cN_c + {\gamma}LN_q)\]

where,

\[\begin{split}\small \begin{array}{lr} c = \mbox{medium cohesion} \\ N_c = 2\sqrt{K_p}(K_p + 1) \\ K_p = (1 + \sin{\phi}) / (1 - \sin{\phi}) \\ \phi = \mbox{soil friction} \\ N_q = K_p^2 \\ \gamma = \mbox{unit weight of the medium} \\ L = \mbox{height of the overburden at the pile-base} \end{array}\end{split}\]

The input value of \(c_s\) for the bearing spring is calculated by dividing \(F_s^{max}\) by the spring effective length \(L_e\),

(3)\[{{F_s^{max}} \over {L_e}} = \mbox{2.22} \times 10^5 \mbox{N\m}\]

and the property of \(\phi_s\) is set to zero.

The data file is shown below. Figure 2 shows the pile capacity has increased.

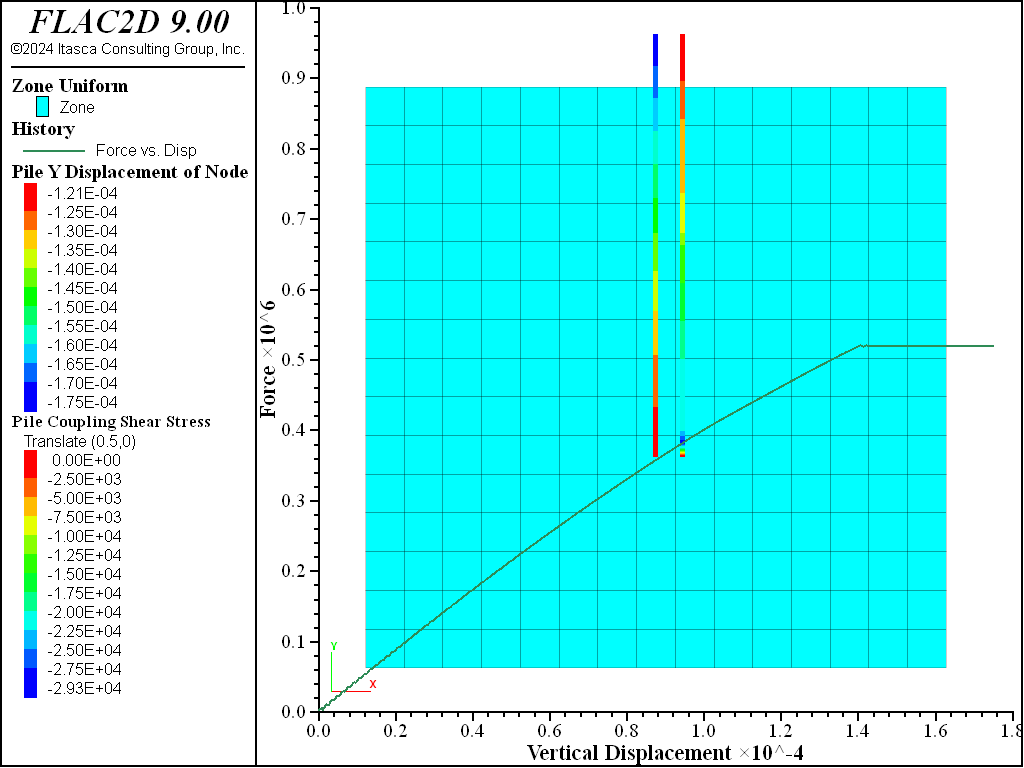
Figure 2: Friction and end-bearing pile: Top force-displacement history and shear stress along shaft.

References

[Coduto1994]

Coduto, D.P. “Foundation Design: Principles and Practices”, Prentice Hall (1994).

[Bishop_et_al.1945]

Bishop, R., R. Hill and N. Mott. “The Theory of Indentation and Hardness Tests”, in Proc. Phys. Soc. Vol. 57, pp 147-159 (1945).

[Johnson1970]

Johnson, K.L. “The Correlation of Indentation Experiments”, in J. Mech. Phys. Solids Vol. 18, pp 115-126 (1970).

[Teh_and_Houlsby1991]

Teh, C.I., and G.T. Houlsby. “An Analytical Study of the Cone Penetration Test in Clay”, in Geotechnique Vol. 41(1) pp 17-34 (1991).

[Cernica1995]

Cernica, J.N. “Foundation Design”, in Geotechnical Engineering. John Wiley (1995).

Data File

EndBearing.dat

; Axially loaded pile example application
model new
model large-strain off
model title "Axially Loaded Pile: End Bearing (2D)"
; Create the grid
zone create quadrilateral size 15 15 edge=11
zone face skin ; Label model boundaries
; Assign constitutive model and propertie
zone cmodel assign elastic
zone property bulk=5e9 shear=1e9 density=2000
; Boundary conditions
zone face apply velocity-normal 0 range group 'East' or 'West'
zone face apply velocity-normal 0 range group 'Bottom'
; Initial conditions
model gravity 10
zone initialize-stresses
model solve ratio-local 1e-4 ; Should be instant
; =======================================================
; Create a pile in the center of the soil block
structure pile create by-line (5.5, 12) (5.5, 4) segments=32
structure pile property young=8.0e10 poisson=0.30 cross-sectional-area=0.7854 ...
                     moi=0.0 perimeter=3.14 ...
                     coupling-stiffness-shear=1.3e11 ...
                     coupling-cohesion-shear=0.0 ...
                     coupling-friction-shear=10.0 ...
                     coupling-stiffness-normal=1.3e11 ...
                     coupling-cohesion-normal=0.0 ...
                     coupling-friction-normal=0.0 coupling-gap-normal=off
; =======================================================
; Specify and apply velocity to pile tip.
structure node fix velocity-x                     range position-y 12 ; node-local system
structure node initialize velocity-x 0.5e-8 local range position-y 12 ; node-local system
; =======================================================
; Set up histories for monitoring model behavior
structure node history name='disp'  displacement-y position (5.5,12)
structure pile history name='force' force-x position (5.5,12)
; =======================================================
structure mechanical damping combined-local
model save 'Initial'
; =======================================================
; Apply velocity to achieve total displacement of 10e-5 m
model cycle 20000
model save 'FrictionPile'

; =======================================================
; Include end-bearing effect
model restore 'Initial'
structure link delete range position-y 4.0
structure link create target zone group 'End' range position-y 4.0
structure link attach x=normal-yield y=free range group 'End'
structure link attach rotation=free range group 'End'
structure link property x area=1.0 stiffness=5.4e11 yield-compression=2.22e5 ...
                                                         range group 'End'
model cycle 35000
model save 'EndBearingPile'