Strength of a Face-Centered Cubic Array of Spheres

Problem Statement

Note

The project file for this example may be viewed/run in PFC.[1] The data files used are shown at the end of this example.

In this problem, the strength of a face-centered cubic array of uniform spheres is determined numerically under axial-symmetry and plane-strain conditions. The array is represented in Fig. 1 and Fig. 2 below. The balls are rigid and have a friction coefficient of 0.3 (corresponding to a friction angle of about 17°). The test results are compared to the analytical solution of [Thornton1979].

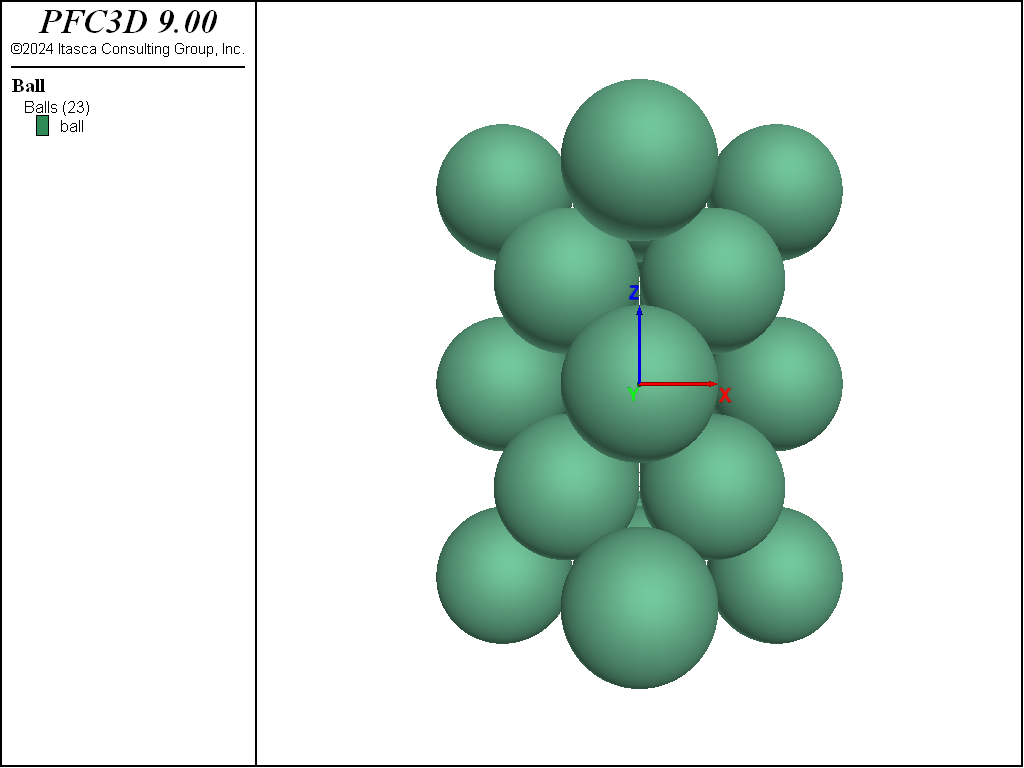
Figure 1: Geometry of face-centered cubic array of spheres, plan view.

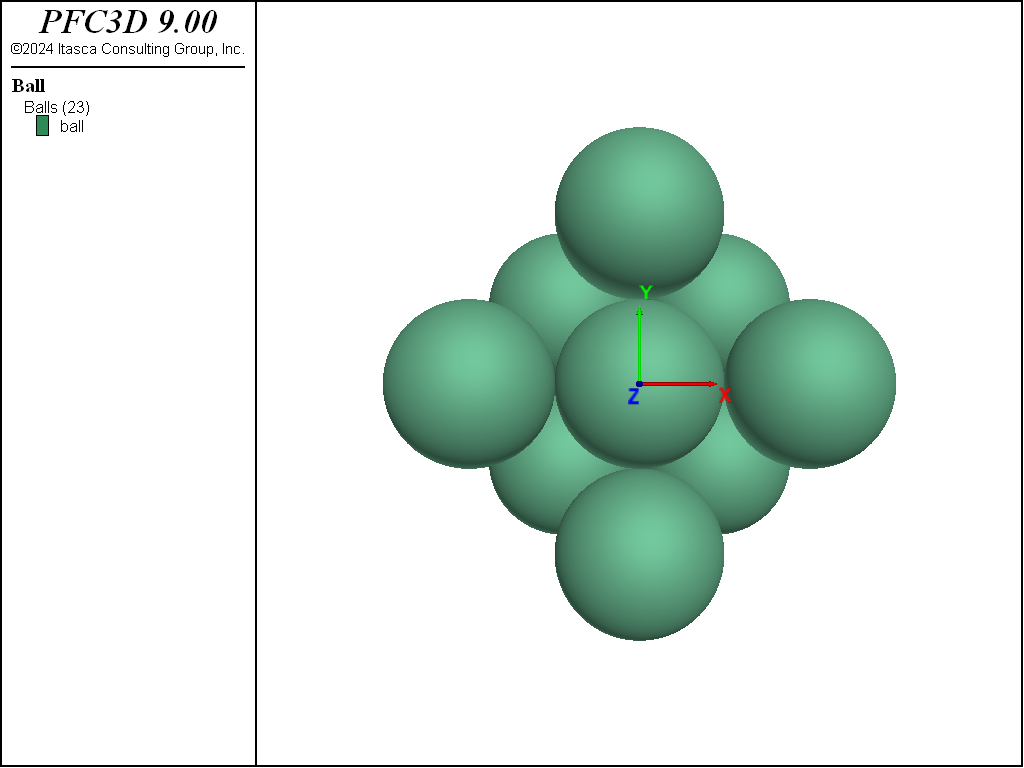
Figure 2: Geometry of face-centered cubic array of spheres, elevation.

Closed-Form Solution

The form of the average stress tensor at failure within a typical sphere has been determined analytically by [Thornton1979] under homogeneous conditions. The failure mechanism, characterized by the formation of gaps along two perpendicular planes, is associated with a normalized strain-increment tensor of the form

(1)\[\begin{split}\begin{bmatrix} 2a & 0 & 0 \\ 0 & 2b & 0 \\ 0 & 0 & -(a+b) \end{bmatrix}\end{split}\]

where \(a + b =\) 1, and the reference axes are defined in Fig. Fig. #planview.

The definition of the average stress tensor in terms of contact forces is the same as that used in PFC3D. In the case where the shear components can be neglected, the stress tensor may be expressed, up to a scalar multiplication factor, in the form

(2)\[\begin{split}\begin{bmatrix} - 1 + 2af/C & 0 & 0 \\ 0 & -1 + 2bf/C & 0 \\0 & 0 & -2-2(a+b)f/C \end{bmatrix}\end{split}\]

where \(f\) is the friction coefficient, and the constant, \(C\), is defined by the relation

(3)\[C = \sqrt{ {{3} \over {2}} (a^2 + b^2) + ab }\]

In axisymmetric conditions, \(a = b = 0.5\), and the ratios of principal stresses at failure, defined as strength measures, are found to be

(4)\[\begin{split}{\sigma_{zz} \over \sigma_{xx}} &= {2(1+f) \over 1-f} \\ \\ \sigma_{yy} \over \sigma_{xx} &= 1\end{split}\]

In plane-strain conditions, \(a =\) 1, \(b =\) 0, and the strength is measured by the following ratios:

(5)\[\begin{split}{\sigma_{zz} \over \sigma_{xx}} &= {2 (\sqrt{3} + \sqrt{2}f) \over \sqrt{3} - 2 \sqrt{2}f} \\ \\ {\sigma_{yy} \over \sigma_{xx}} &= {\sqrt{3} \over \sqrt{3} - 2 \sqrt{2}f}\end{split}\]

PFC3D Model

The numerical model configuration consists of an assembly of 23 balls with common radius, \(r\), as depicted in Fig. Fig. #planview and Fig. Fig. #elevation above. For easy reference, we use the terms outer-\(x\), outer-\(y\) and outer-\(z\) to indicate the balls with origin at \(|x| = 2r\), \(|y| = 2r\), and \(|z| = 2\sqrt{2r}\), respectively. All balls have the same properties:

Table 1: Properties

density	2000	\([M/L^3]\)
normal stiffness	5 × 1011	\([M/T^2]\)
shear stiffness	5 × 1011	\([M/T^2]\)
friction coefficient	0.3
radius	20	\([L]\)

The lateral boundary conditions of the test are prescribed as follows. In both axisymmetric and plane-strain conditions, compressive forces of the magnitude \(F\) are applied to the outermost balls in the \(x\)-direction. Compressive forces of the same magnitude \(F\) are applied to the outermost balls in the \(y\)-direction in the axisymmetric test, while the \(y\)-velocity is fixed to zero in the plane-strain test. The axial conditions are prescribed, in turn, by means of imposed compressive velocity in the \(z\)-direction to the outer-\(z\) balls.

In the numerical experiments, the velocity of the top and bottom balls is first fixed to zero, the ball friction coefficient is set to a low value of \(1 × 10^5\), the lateral boundary conditions are applied using \(F =1 \times 10^6\) in both the axisymmetric and plane-strain tests, and the system is cycled to equilibrium. The ball friction coefficient is then set to 0.3. A compressive velocity of magnitude \(|v_z|= 0.5 \times 10^4\) is applied to the outer-\(z\) ball in the \(z\)-direction, and failure of the system is monitored using a plot of principal stress histories in terms of a measure of strain in the \(z\)-direction. Ball rotations are fixed throughout the tests. Failure is identified on the \(σ_{zz}\) plot by a peak in the stress-strain curve. Records of the stress ratio at that time are used to provide numerical values for the comparison.

Results and Discussion

A comparison of the numerical test results with the analytical predictions derived from Equations (4) and (5), using \(f = 0.3\), is presented in Table 2 and Table 3. The agreement is good, with a relative error of less than 1% for both the axisymmetric and the plane-strain tests.

Table 2: Strength Comparison, Axisymmetric Case

	Numerical	Analytical	Relative error
\(\sigma_{zz} / \sigma_{xx}\)	3.7142	3.7143	< 1%
\(\sigma_{yy} / \sigma_{xx}\)	1.0000	1.0000	< 1%

Table 3: Strength Comparison, Plane-strain case

	Numerical	Analytical	Relative error
\(\sigma_{zz} / \sigma_{xx}\)	4.8809	4.8812	< 1%
\(\sigma_{yy} / \sigma_{xx}\)	1.9603	1.9604	< 1%

References

[Thornton1979] (1,2)

Thornton, C. “The Conditions for Failure of a Face-Centered Cubic Array of Uniform Rigid Spheres,” Géotechnique, 29 (4), 441-459 (1979).

Data Files

Array_Strength.dat (3D)

; fname: array_strength.dat (3D)
;
;     Strength of face-centered cubic array of rigid spheres
;     Axisymmetric and plane-strain cases
;=========================================================================
model new
model large-strain on
fish define c_para
; --- input ---
  global radb = 20
  global conf_p = 1.e6
  global pzvel = 0.0
  global mzvel = 0.0
; --- calculation ---
  global dhz   = math.sqrt(2) * radb
  global small = radb * 0.01
  global drang = radb * 0.5
  global height = 4.0 * dhz
  global zt1 = 2.0 * dhz - drang
  global zt2 = 2.0 * dhz + drang
  global zb1 = - zt2
  global zb2 = - zt1
  global yt1 = radb * 1.5
  global yt2 = radb * 2.5
  global yb1 = - yt2
  global yb2 = - yt1

  command
    model domain extent [-5.0*radb] [5.0*radb] ...
                        [-5.0*radb] [5.0*radb] ...
                        [-5.0*radb] [5.0*radb] ...
           condition destroy destroy destroy
  endcommand
end
; --- measurement circle ---
fish define c_mes
   global radi = radb + small
   command
      measure create id 1 radius [radi]
   end_command
   global mp = measure.find(1)
end

fish define c_stres
   global mstr = measure.stress(mp)
   global c_s11 = mstr(1,1)
   global c_s22 = mstr(2,2)
   global c_s33 = mstr(3,3)
   global c_s12 = mstr(1,2)
   global c_s13 = mstr(1,3)
   global c_s23 = mstr(2,3)
   global c_s21 = mstr(2,1)
   global c_s31 = mstr(3,1)
   global c_s32 = mstr(3,2)

  if c_s11 < c_s22 then
    global c_s1 = c_s11
    global c_s2 = c_s22
  else
    c_s1 = c_s22
    c_s2 = c_s11
  end_if
  if c_s2 < c_s33 then
    global c_s3 = c_s33
  else
    if c_s1 < c_s33 then
      c_s3 = c_s2
      c_s2 = c_s33
    else
      c_s3 = c_s2
      c_s2 = c_s1
      c_s1 = c_s33
    end_if
  end_if
  global c_r1 = 0.0
  if c_s3 # 0.0 then
    c_r1 = c_s1 / c_s3
  end_if
  global c_r2 = 0.0
  if c_s3 # 0.0 then
    c_r2 = c_s2 / c_s3
  end_if
end

fish define g_large
  global dis   = 2. * radb
  global dism  = - dis
  global numid = numid + 1
  command
    ball create id [numid] position-x 0. position-y [dis]  ...
                          position-z [zb] radius [radb]
  end_command
  numid = numid + 1
  command
    ball create id [numid] position-x [dism] position-y 0. ...
                          position-z [zb] radius [radb]
  end_command
  numid = numid + 1
  command
    ball create id [numid] position-x 0. position-y 0.    ...
                          position-z [zb] radius [radb]
  end_command
  numid = numid + 1
  command
    ball create id [numid] position-x [dis] position-y 0.  ...
                          position-z [zb] radius [radb]
  end_command
  numid = numid + 1
  command
    ball create id [numid] position-x 0. position-y [dism] ...
                          position-z [zb] radius [radb]
  end_command
end

fish define g_small
  global radbm = - radb
  global numid = numid + 1
  command
    ball create id [numid] position-x [radbm] position-y [radb]  ...
                          position-z [zb] radius [radb]
  end_command
  numid = numid + 1
  command
    ball create id [numid] position-x [radb] position-y [radb]   ...
                          position-z [zb] radius [radb]
  end_command
  numid = numid + 1
  command
    ball create id [numid] position-x [radbm] position-y [radbm] ...
                          position-z [zb] radius [radb]
  end_command
  numid = numid + 1
  command
    ball create id [numid] position-x [radb] position-y [radbm]  ...
                          position-z [zb] radius [radb]
  end_command
end

fish define g_pack
  global zb = - 2. * dhz
  g_large
  global z1 = zb - small
  global z2 = zb + small
  command
    ball extra 1 0 range position-z [z1] [z2]
  end_command
  zb = -dhz
  g_small
  z1 = zb - small
  z2 = zb + small
  command
    ball extra 1 1 range position-z [z1] [z2]
  end_command
  zb = 0.
  g_large
  z1 = zb - small
  z2 = zb + small
  command
    ball extra 1 0 range position-z [z1] [z2]
  end_command
  zb = dhz
  g_small
  z1 = zb - small
  z2 = zb + small
  command
    ball extra 1 1 range position-z [z1] [z2]
  end_command
  zb = 2. * dhz
  g_large
  z1 = zb - small
  z2 = zb + small
  command
    ball extra 1 0 range position-z [z1] [z2]
  end_command
end

fish define c_press
  global d1 = 0.5 * radb
  global d2 = 2.1 * radb
  global c_v = - conf_p
  command
    ball attribute force-applied-x [c_v] range position-x [d1] [d2]
    ball attribute force-applied-y [c_v] range position-y [d1] [d2]
  end_command
  d1 = -d1
  d2 = -d2
  c_v = conf_p
  command
    ball attribute force-applied-x [c_v] range position-x [d2] [d1]
    ball attribute force-applied-y [c_v] range position-y [d2] [d1]
  end_command
end

fish define strain_mes
  global verdis = verdis + pzvel * global.timestep
  global e1 = 2. * verdis / height
  global c_t = global.timestep
end

fish define c_comp
  c_press
  command
    ball property 'fric' 1.e-5
    fish callback add c_stres    -1.0
    fish callback add strain_mes -1.0
    model cycle 300
  endcommand
end

fish define c_load
  pzvel = 0.5e-4
  mzvel = -0.5e-4
  command
    history interval 1
    ball property 'fric' 0.3
    ball attribute velocity-z [pzvel] range position-z [zb1] [zb2]
    ball attribute velocity-z [mzvel] range position-z [zt1] [zt2]
    model cycle 700
  endcommand
end
; --- choose contact model
contact cmat default model Linear
; --- generate geometrical constants ---
[c_para]
; --- create ball assembly ---
[g_pack]
; --- create measurement sphere ---
[c_mes]
; --- histories ---
fish history c_t
fish history e1
fish history c_r1
fish history c_r2
fish history c_s33
fish history c_s22
fish history c_s11
fish history c_s12
fish history c_s13
fish history c_s23
; --- property set up ---
ball attribute density 2000 damp 0.7
ball property 'kn' 5e11 'ks' 5e11
model clean
; --- fix top and bottom layers ---
ball fix velocity-z range position-z [zb1] [zb2]
ball fix velocity-z range position-z [zt1] [zt2]
ball fix spin-x spin-y spin-z range position-z [zb1] [zt2]
model save 'ini'

;--------------------------------------------------------------------------
;--------------            Axisymetry case                    -------------
;--------------------------------------------------------------------------

; --- compaction phase ---
[c_comp]
; --- loading phase ---
[c_load]
; --- check results ---
[c_stres]
fish list [c_r1] [c_r2]
model save 'as'

;--------------------------------------------------------------------------
;--------------           Plane-strain case                   -------------
;--------------------------------------------------------------------------
model restore 'ini'

; --- fix front and back layers ---
ball fix velocity-y range position-y [yb1] [yb2]
ball fix velocity-y range position-y [yt1] [yt2]
ball fix velocity-y range position-z [dhz-small] [dhz+small]
ball fix velocity-y range position-z [-1.0*dhz-small] [-1.0*dhz+small]

; --- compaction phase ---
[c_comp]
; --- loading phase ---
[c_load]
; --- check results ---
[c_stres]
fish list [c_r1] [c_r2]
model save 'ps'

program return
;==========================================================================
;eof: array_strength.dat (3D)

Endnote

[1]

This example is listed under the present document title in the i Examples dialog (use the menu command Help -> Examples… to access).