Cable-Reinforced Beam
Problem Statement
Note
The project file for this example may be viewed/run in 3DEC.[1] The data files used are shown at the end of this example.
This example illustrates the behavior of a simply supported, lightly reinforced beam subjected to gravity loading. Cable elements are used to represent the reinforcement.
A vertical crack is created through the beam center by adding a zero-strength interface. If the model is run without reinforcement (by removing the structure cable create commands), the system behaves as two separate pieces that separate at the interface. The two blocks are supported on rollers; thus, they can move away from one another as the system collapses (see Figure 1).
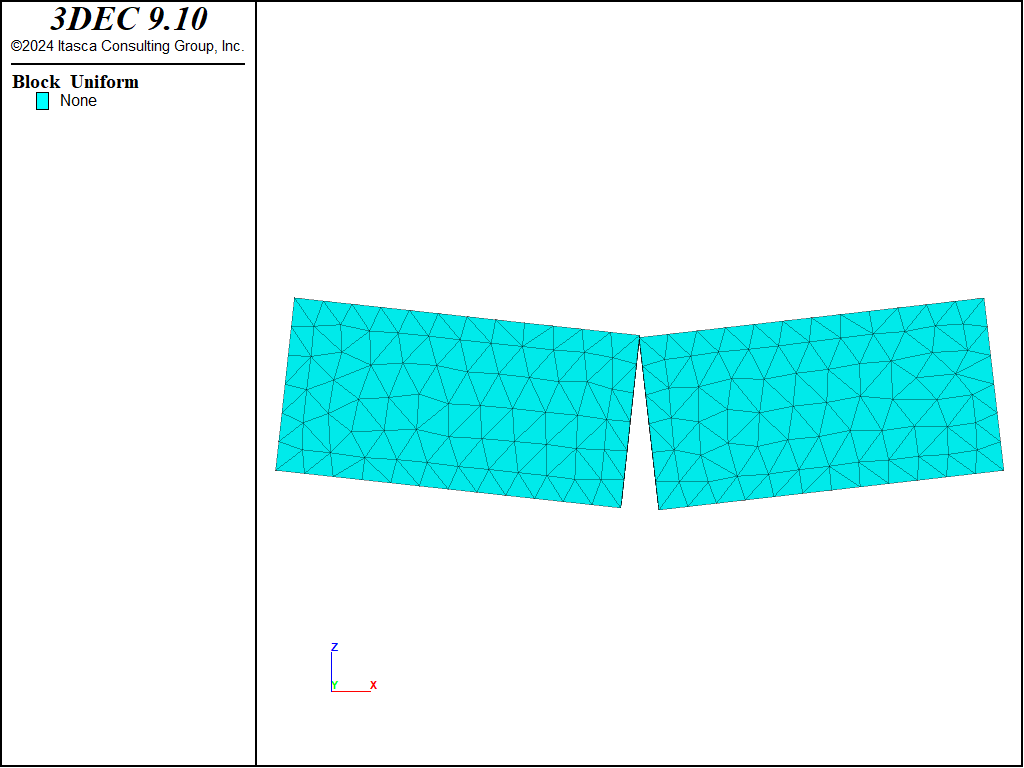
Figure 1: Structural configuration after 3000 cycles (no cable present).
If the model is rerun with a cable inserted within the beam near its bottom fiber, then the cable carries the tension that develops in the lower portion of the beam. The final axial force distribution in the cable after the model has stabilized is shown in Figure 2. These tensile forces in the cable are produced by the grout stresses that have developed along the cable length (see Figure 3). The maximum vertical center line displacement is approximately 10 mm.
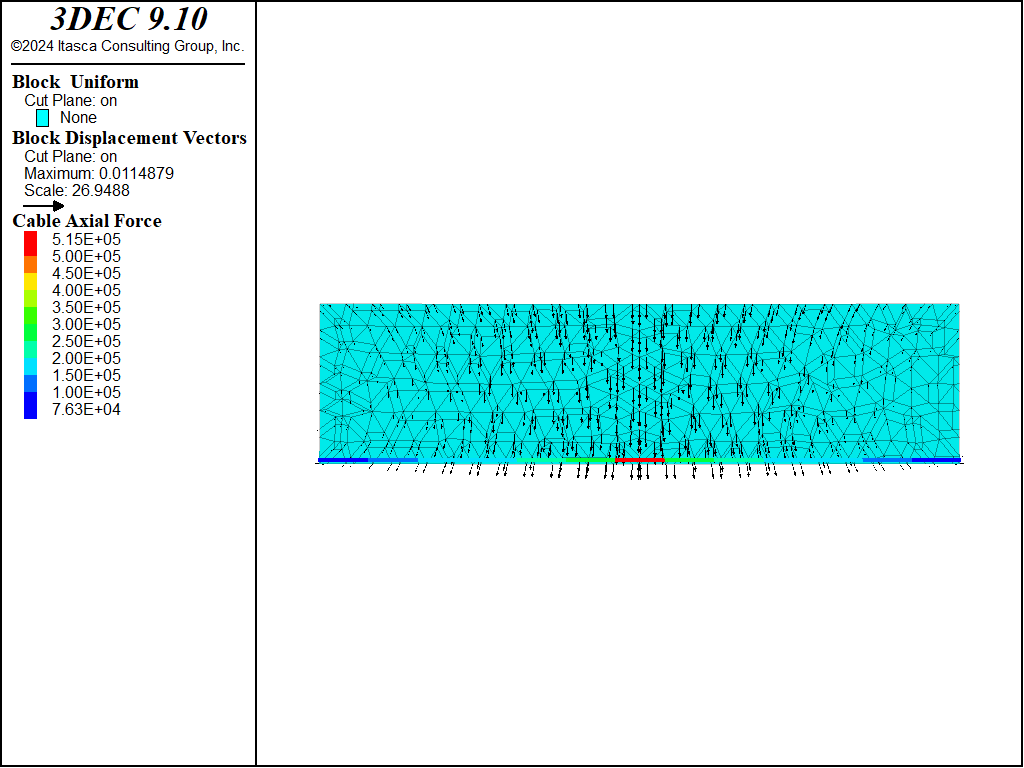
Figure 2: Final axial force distribution in cable.
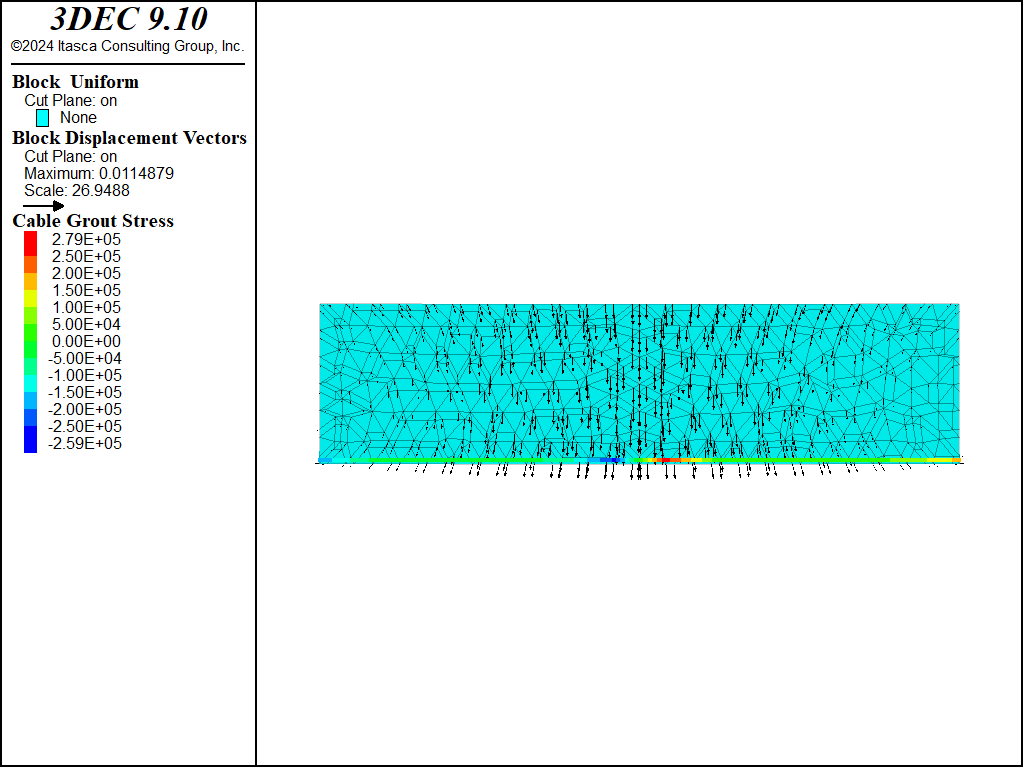
Figure 3: Final grout stress distribution.
The average axial direction of the cable goes from left to right, corresponding with the orientation of the points given with the structure cable create by-line command. In Figure 3, we see that the grout stresses are positive on the right side of the cable and negative on the left side of the cable. These values can be printed with the structure cable list grout command.
In the previous model, the grout cohesive strength was set to a very large value to prevent grout failure. If we set the grout cohesive strength equal to 1.5 × 105 N/m and rerun the model, we find that the system still stabilizes; however, during the loading process, the grout yields (cable slips) in the middle region (see Figure 4). The grout stress in this region is equal to the grout cohesive strength (see Figure 5), the tensile force is distributed farther along the cable (compare Figure 2 and Figure 6), and the maximum vertical centerline displacement has increased from 10 mm to 11.8 mm.
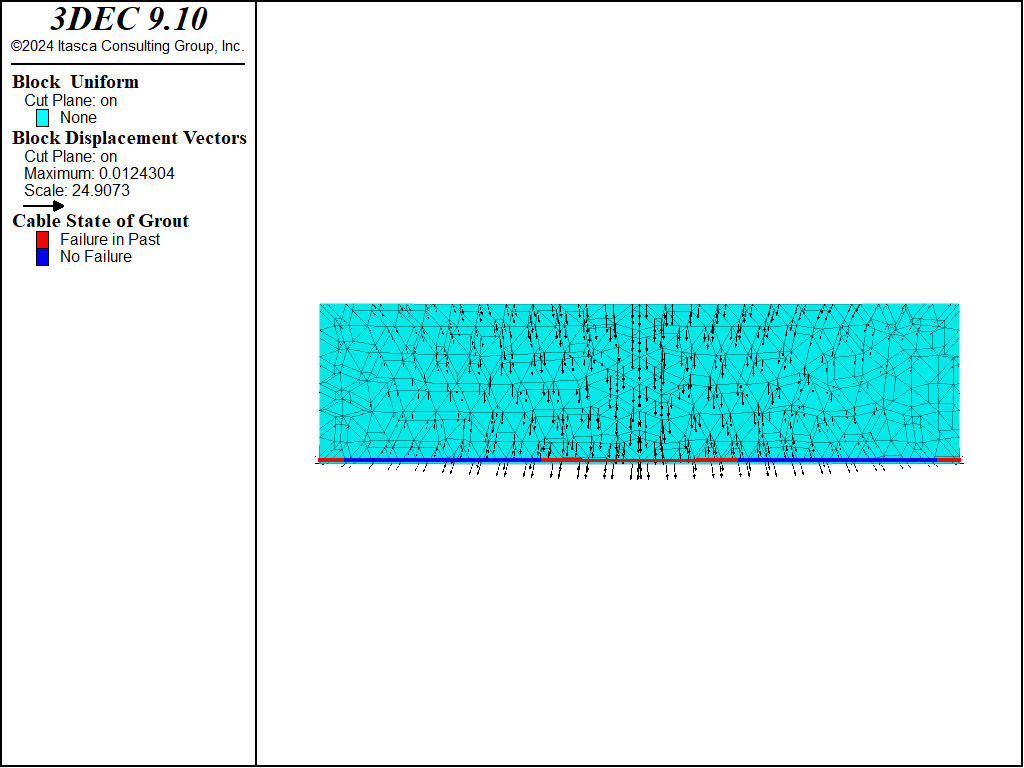
Figure 4: Final grout slip state (reduced grout cohesive strength).
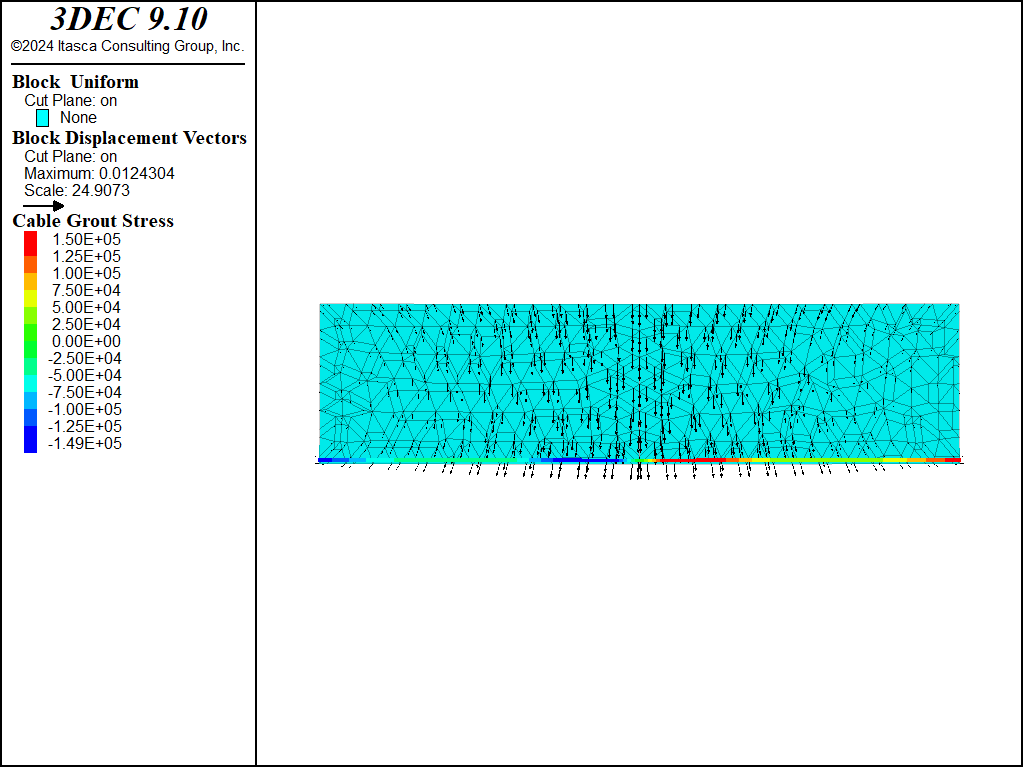
Figure 5: Final grout stress distribution (reduced grout cohesive strength).
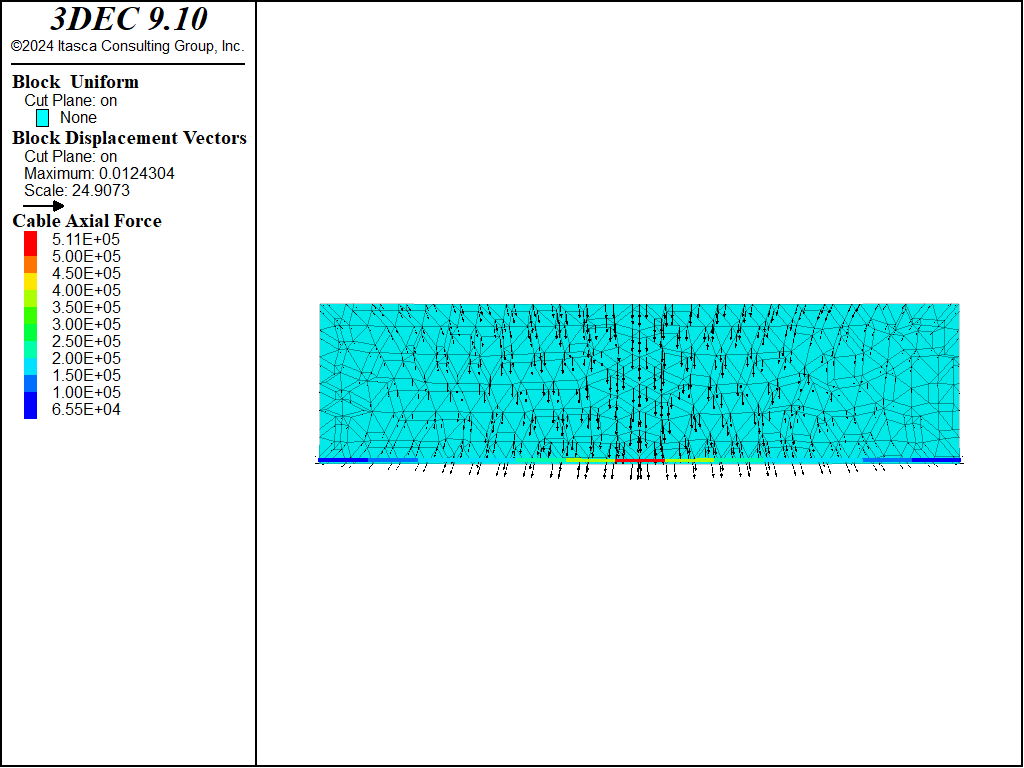
Figure 6: Final axial force distribution in cable (reduced grout cohesive strength).
Data File
ReinforcedBeam.dat
model new
model large-strain on
model random 10000
model title "Cable-reinforced beam"
; Create beam (composed of zones)
block create brick 0 6 0 1 0 3
block create brick 6 12 0 1 0 3
block zone generate edgelength 0.5
; Joint properties
block contact property stiffness-normal 1e10 stiffness-shear 1e10
block contact material-table default property stiffness-normal 1e10 ...
stiffness-shear 1e10
; Zone properties
block zone cmodel assign elastic
block zone property bulk 1e9 shear .3e9 density 2400
; Boundary conditions - pin on right and left lower corners
block gridpoint apply velocity-z 0 range position-z 0 position-x 0
block gridpoint apply velocity-z 0 range position-z 0 position-x 12
; Gravity
model gravity 10
model save 'Start'
======================================================
; Run problem with no cable present
block mechanical damping combined
model cycle 3000
model save 'NoCable'
==================================================
; Now rerun problem with a cable present
model restore 'Start'
; Create Cable and set properties
structure cable create by-line (0.1, 0.5, 0.1) (11.9, 0.5, 0.1) id=1 segments=13
structure cable property cross-sectional-area=2e-3 young=200e9 ...
yield-tension=1e20 grout-stiffness=1e10 ...
grout-cohesion=1e20
block mechanical damping combined
model solve ratio 1e-4
model save 'Cable'
=====================================================
; Now allow the cable to fail
structure cable property grout-cohesion 1.5e5
model solve ratio 1e-4
model save 'CableFail'
Endnote
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
