Advancing Lined Tunnel (Slip at Liner-Soil Interface)
Problem Statement
Note
The project file for this example may be viewed/run in 3DEC.[1] The data files used are shown at the end of this example.
This example demonstrates how to simulate the sequential operations of excavating and adding support to an advancing tunnel. The tunnel has a circular cross-section of 1 meter radius and is located at 5 meter depth in a soft elastic soil (\(K = 50\ \rm MPa\), \(G = 18\ \rm MPa\)) with isotropic in-situ stresses of 1 MPa. The tunnel is supported by shotcrete (\(E = 10.5\ \rm GPa\), \(\nu = 0.25\)) with a 200 mm thickness. The shotcrete remains elastic; however, the liner-soil interface can separate and/or slip. This example replicates the Lined Tunnel (with shell elements) example, but replaces the shell elements used in that example with the liner elements used here. The shell elements provide a rigid connection with the soil, whereas the liner elements provide a connection that allows slip to occur and a gap to form. In this example, first a large cohesive strength is assigned to the soil-liner interface to reproduce the rigid behavior from the shell-element version. The model is then rerun with the cohesive strength set to zero, and we observe the slip and resulting stress redistribution.
Begin with an initial tunnel of 2 meter total length. For simplicity, it is assumed that the excavation proceeds simultaneously on both tunnel faces; therefore, it is only necessary to model one quarter-section of the tunnel by applying symmetry boundary conditions on the three symmetry planes. (Specifying the
proper symmetry conditions to the nodes on these planes requires first aligning the node-local systems, as
described below.) The excavation process is modeled by assigning the null material model to zones, and then
allowing the stresses to redistribute (see Figure 1). The shotcrete is now installed by creating liner elements and attaching them to the tunnel surface with the structure liner create by-block-face command. The next tunnel segment is excavated and, again, the stresses are allowed to redistribute. The model at this stage is shown in Figure 2. This excavation sequence can be repeated to model the entire tunnel-construction process.

Figure 1: Stage 1: Excavate material in section 1.

Figure 2: Stage 2: Install shotcrete in section 1; excavate material in section 2.
There are three symmetry planes in this model. Symmetry boundary conditions (zero displacement normal to
the plane, and zero rotation about two axes that lie in the plane) must be specified for the nodes that
lie upon these planes. These conditions are specified using the structure node fix command;
however, this command operates on the degrees of freedom associated with the node-local system, and the
node-local systems of all nodes used by liner elements are set automatically at the start of a set of
cycles (or when the model cycle 0 command is executed), such that the \(z\)-axis is
aligned with the average normal direction of all liner elements using the node. For this model, the default orientations are shown in Figure 3. The true liner normal direction on the \(x = 0\) plane is vertical, but because only one-quarter of the system is modeled, the liner normal direction on this plane is perpendicular to the plane defined by the liners included in the model, which are only in the \(x \geq 0\) region. This normal direction is not vertical. Nodes lying on the \(x = 0\) and \(z = 0\) planes must be reoriented in order to specify the proper symmetry boundary conditions. This is accomplished with the commands:
struct node system-local x (1,0,0) y (0,-1,0) range position-x 0
struct node fix system-local range position-x 0
struct node fix velocity-x rotation-y rotation-z range position-x 0
struct node system-local x (0,0,-1) y (0,-1,0) range position-z 0
struct node fix system-local range position-z 0
struct node fix velocity-x rotation-y rotation-z range position-z 0
struct node fix velocity-y rotation-x rotation-z range position-y 0
These commands realign and then fix the appropriate node-local systems and also specify the proper
velocity-fixity conditions. The realigned systems must be fixed with the
structure node fix system-local command in order to prevent automatic realignment to the default
orientation during the next set of cycles. The final realigned and fixed node-local system orientations are shown in Figure 4.
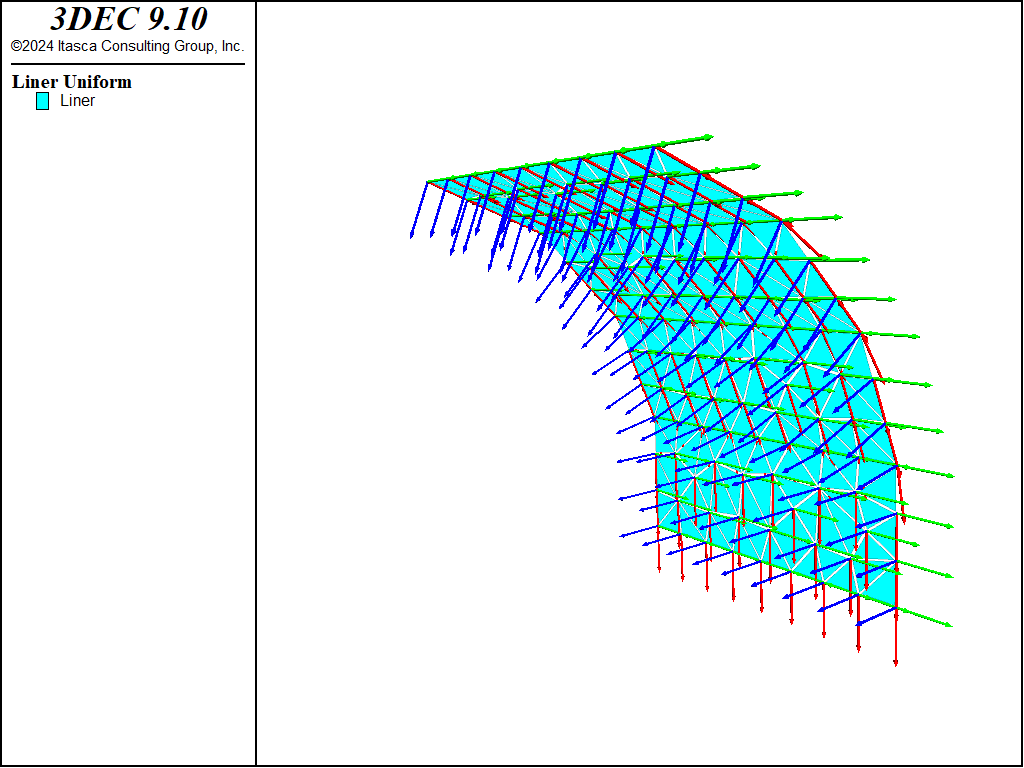
Figure 3: Default orientation of node-local systems.
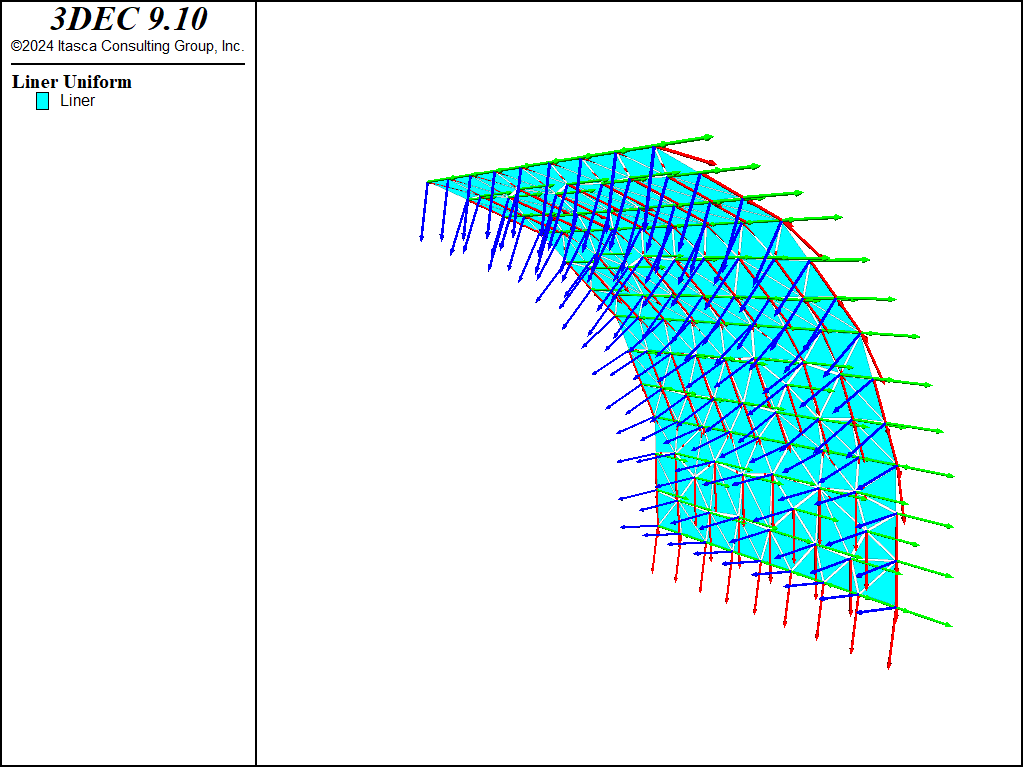
Figure 4: Orientation of node-local systems after realignment.
The liner-zone interface stiffnesses (\(k_n\) and \(k_s\)) are set equal to 7.4 × 1010 N/m3 to ensure that the interface deformation is small relative to the zone deformation using the liner-stiffness equation, and increasing the value by a factor of 100, as suggested in the text following this equation. We will confirm below that the interface deformation is small relative to the zone deformation.
In the first run, an effectively infinite cohesive strength is assigned to the liner-zone interface. The behavior of this model should be like the behavior of the rigidly connected system. Figures 5 and 6 show the displacement of the soil during the second excavation stage for the cases with and without support. The \(z\)-displacement history at the tunnel crown (\(z\) is vertical) is included in each figure. The shotcrete support reduces the crown displacement from approximately 12 mm to 1 mm. This is the same behavior as that of the rigidly connected system.
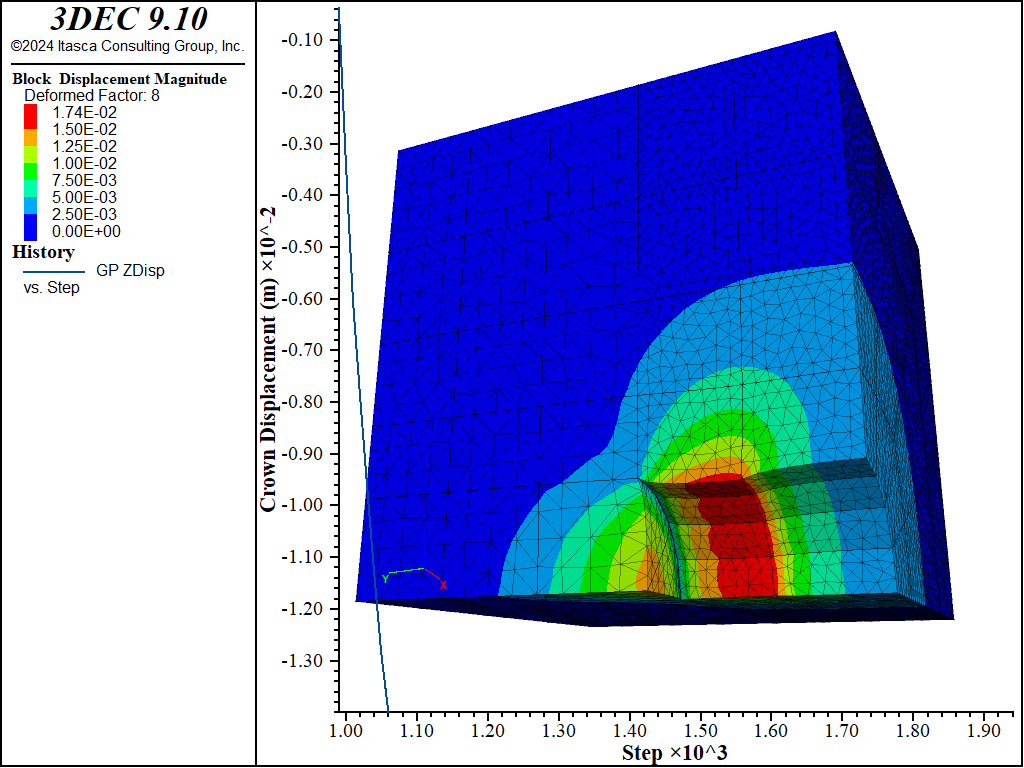
Figure 5: Displacement of the soil (deformation factor: 8) during stage 2 — no support.
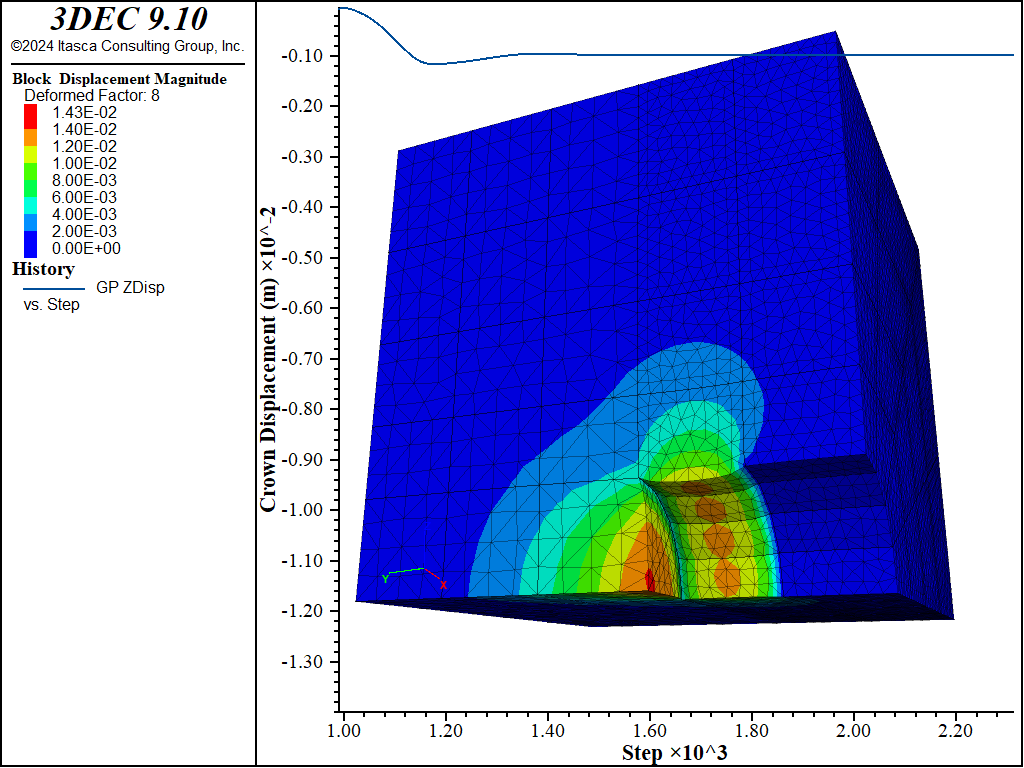
Figure 6: Displacement of the soil (deformation factor: 8) during stage 2 — shotcrete support (liner-zone cohesion of 1020).
The deformation arising from the excavation of material in section 2 forces the front of the liner to pinch inwards (see Figure 7). This pinching induces a thrust in the circumferential direction (see Figure 8). The thrust is measured by the membrane stress resultant \(N_y\), where the \(y\)-direction lies along the tunnel circumference. We see that the thrust is compressive, and that it is largest at the front of the liner and decreases with increasing distance from the front. This response mirrors that of the pinching deformation, with greater pinching inducing greater thrust.
These two figures can be compared with the corresponding figures from the rigidly connected system. The close similarity indicates that the liner elements with infinite cohesion are behaving like the shell elements (which are rigidly connected to the zones).
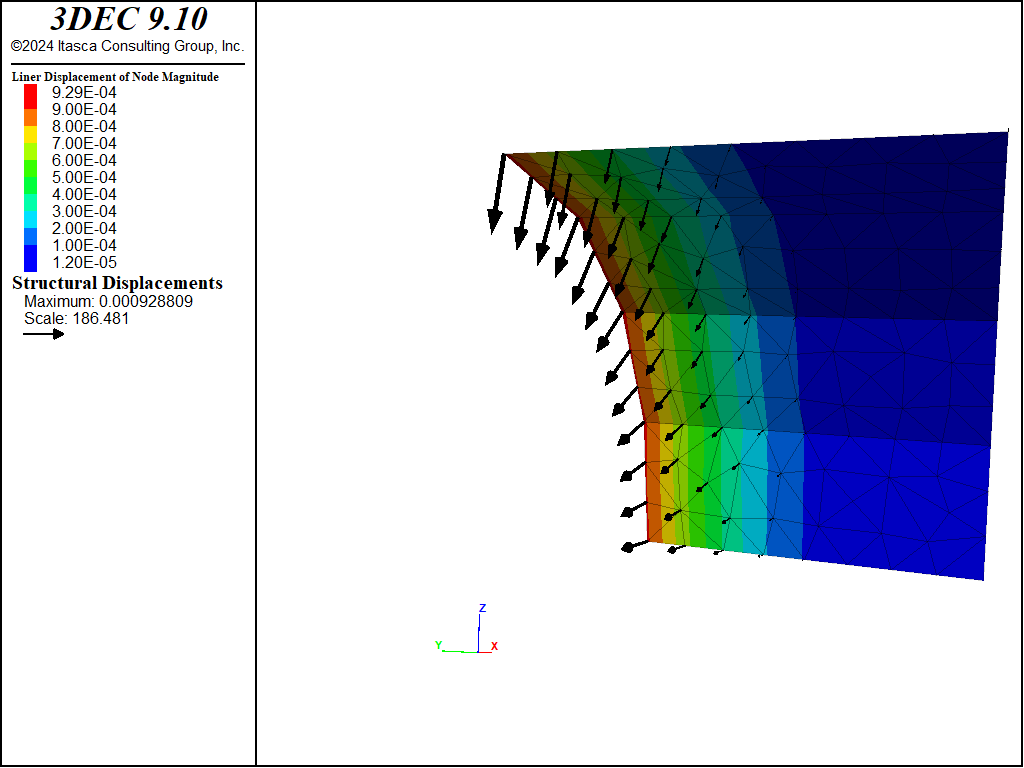
Figure 7: Pinching deformation in the liner at end of stage 2 (liner-zone cohesion of 1020).
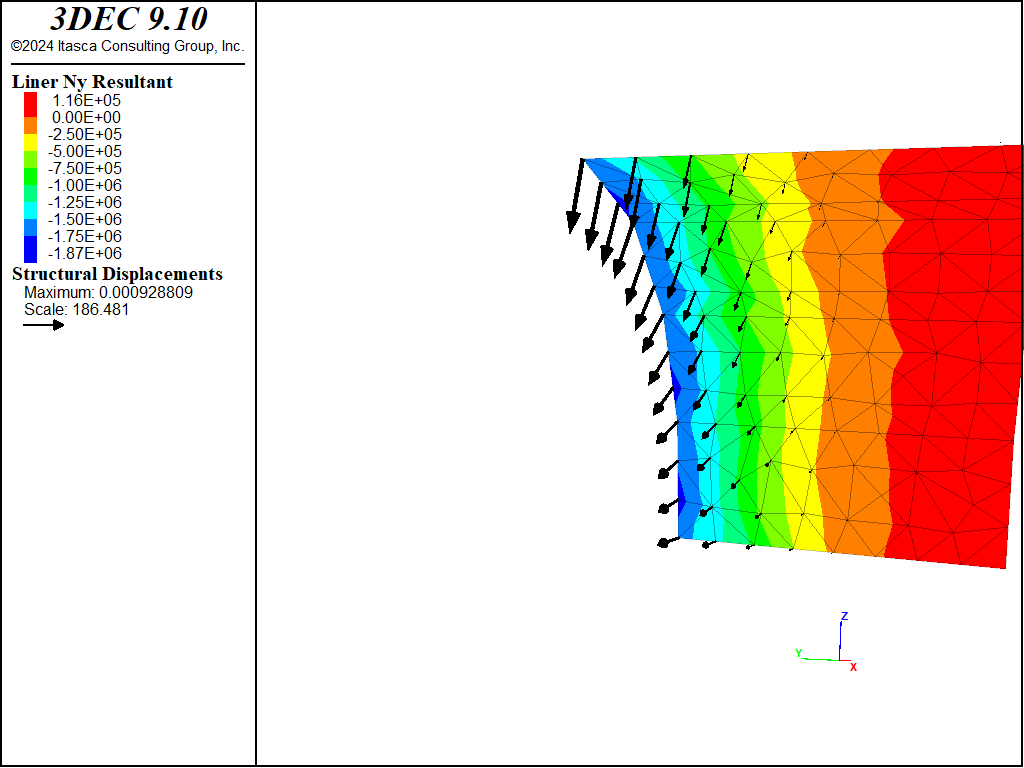
Figure 8: Thrust in the liner at end of stage 2 (liner-zone cohesion of 1020).
We confirm that the interface deformation is small relative to the zone deformation (and thus confirm that our values of \(k_n\) and \(k_s\) are large enough) by plotting the normal displacement of the gridpoint, node and coupling spring at the tunnel crown (see Figure 9). If the model is rerun with values of \(k_n\) and \(k_s\) that are 100 times smaller than the current values, it is found that the interface deformation is no longer small relative to the zone deformation (see Figure 10). This leads to lower loads being carried in the liner, with the maximum thrust, \(N_y\), being reduced by 31% (compare Figures 8 and 11). In order to obtain the proper system response, the values of \(k_n\) and \(k_s\) must be large enough to keep the interface deformation small relative to the zone deformation.
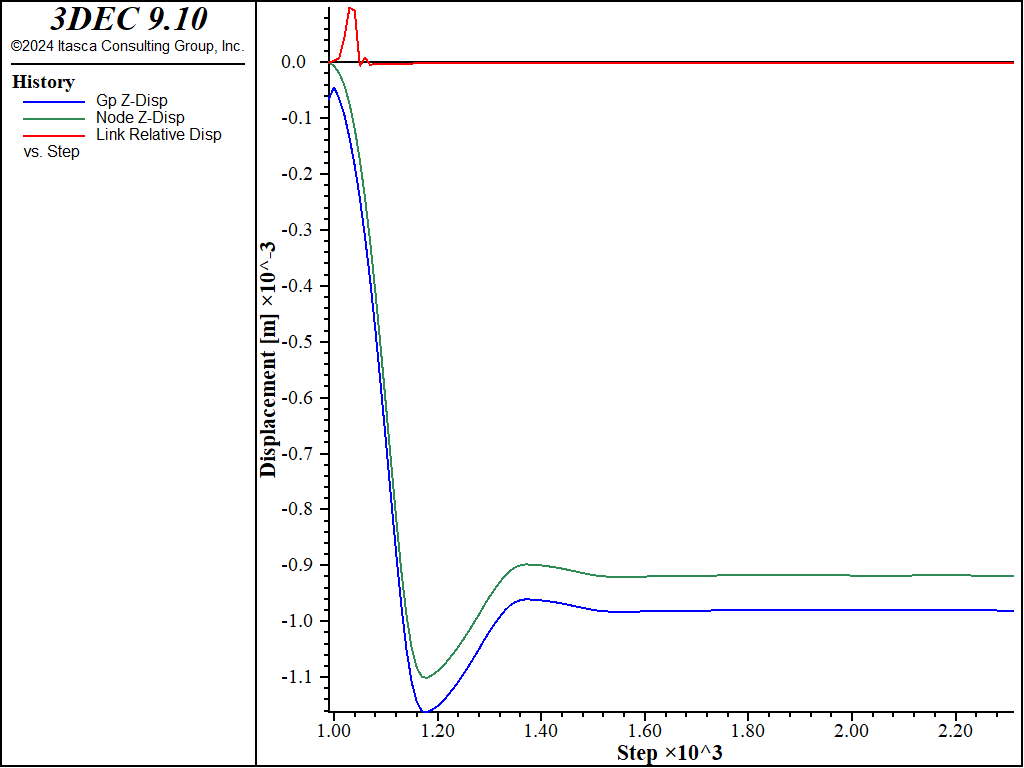
Figure 9: Normal displacement of gridpoint, node, and coupling spring at tunnel crown at end of stage 2 (liner-zone cohesion of 1020).
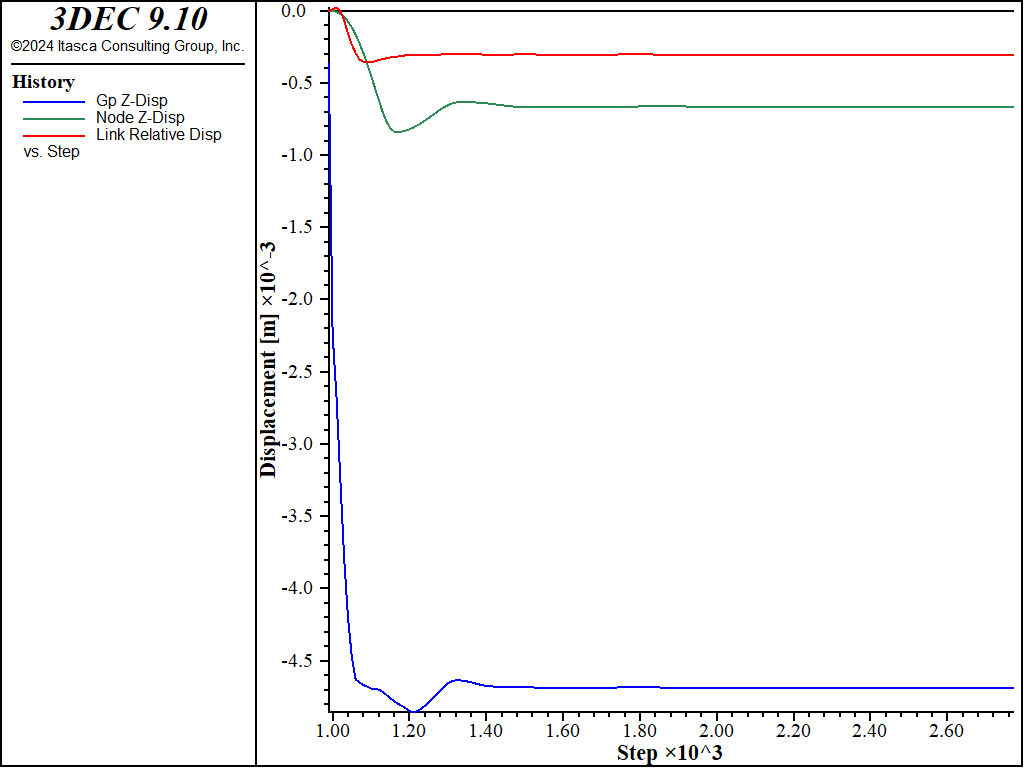
Figure 10: Normal displacement of gridpoint, node, and coupling spring at tunnel crown at end of stage 2 (\(k_n\) and \(k_s\) reduced by factor of 100; liner-zone cohesion of 1020).
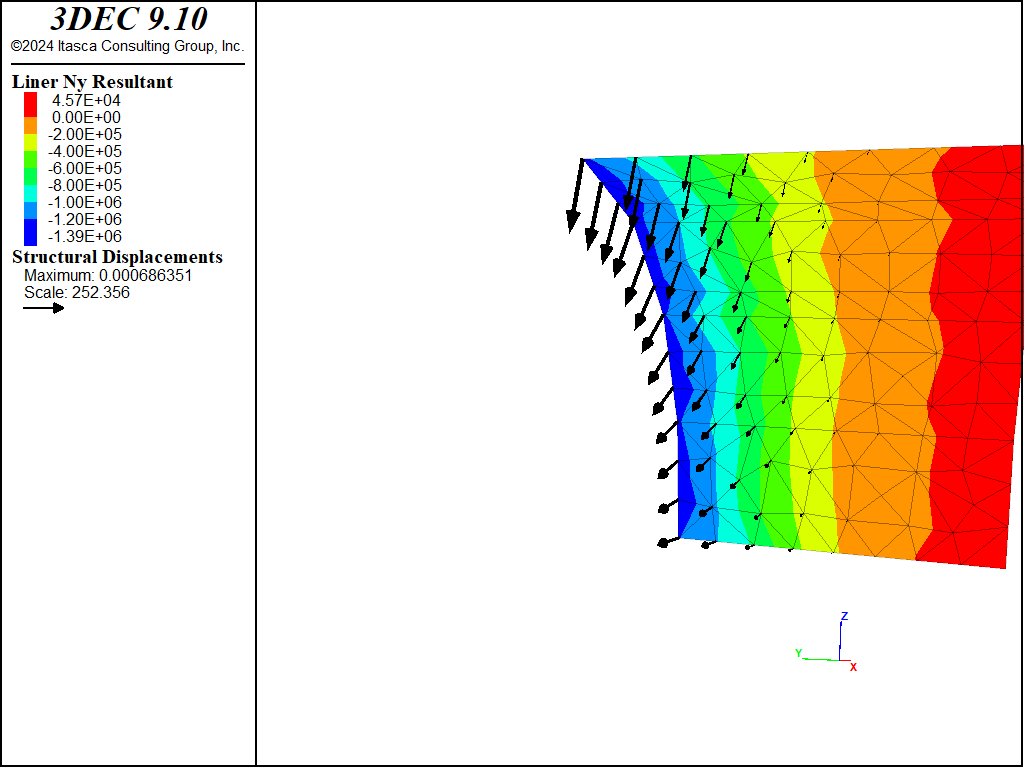
Figure 11: Thrust in the liner at end of stage 2 (\(k_n\) and \(k_s\) reduced by factor of 100; liner-zone cohesion of 1020).
The normal and shear stresses acting on the liner at the end of stage 2 are shown in Figures 12 and 13. Both stresses are largest near the front of the liner near the tunnel face. These stresses are causing the pinching deformation seen in Figure 7. If the cohesive strength of the soil-liner interface is set to zero and cycled to equilibrium, it is observed that the liner springs back away from the tunnel face (see Figure 14) as the shear stresses acting on the liner go to zero. The normal stresses and thrust acting on the liner are only minimally affected.

Figure 12: Normal stress acting on liner surface at end of stage 2 (liner-zone cohesion of 1020).
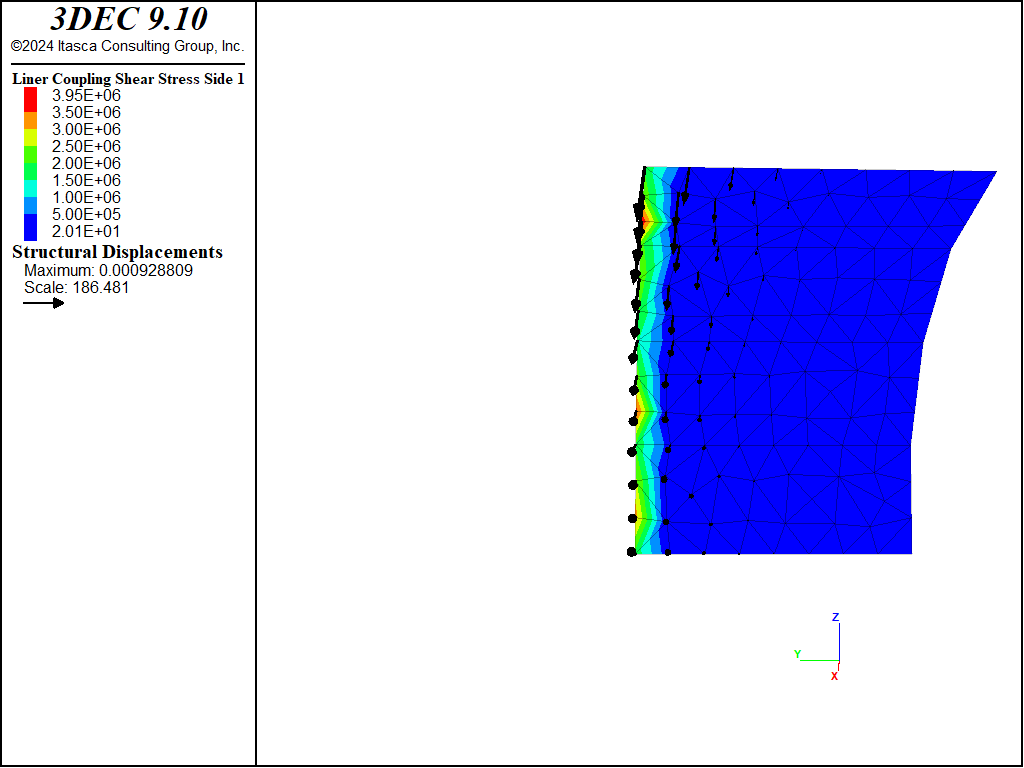
Figure 13: Shear stress acting on liner surface at end of stage 2 (liner-zone cohesion of 1020).
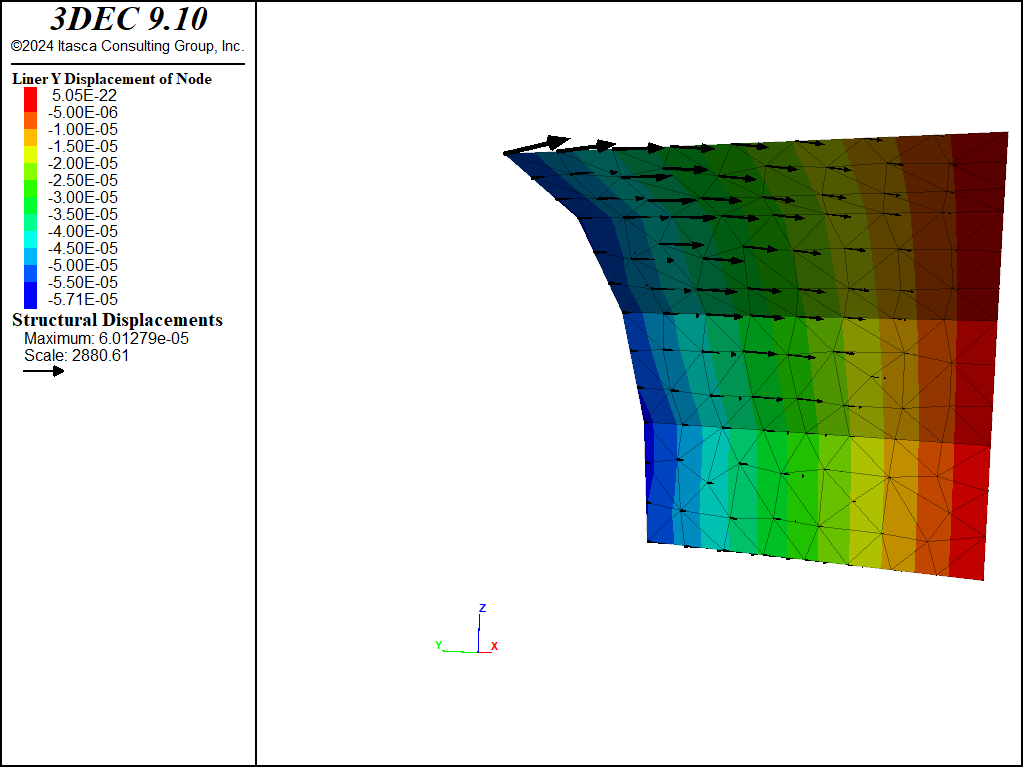
Figure 14: Liner displacement produced by setting the liner-zone cohesion to zero after stage 2.
One additional excavation stage is performed. The model at the end of this stage is shown in
Figure 15. The shotcrete support has been extended into tunnel section 2 by
issuing another structure liner create by-block-face command and specifying an ID number for the new liner segment that differs from the ID number of the liner segment in tunnel section 1. This creates a “cold-joint” between the two liner segments.[2] The deformation that occurs during stage 3 begins to load the new liner segment and produces additional load in the previous liner segment. The thrust field is discontinuous across the joint (see Figure 16).

Figure 15: Stage 3: Install shotcrete in section 2; excavate material in section 3.

Figure 16: Thrust in the liner at end of stage 3 (liner-zone cohesion of zero).
Data File
AdvancingLinedTunnel.dat
; SEL Liner example application :
; Advancing Lined Tunnel with Slip at Liner-Soil interface
model new
model random 10000
model large-strain off
fish automatic-create off
model title 'Advancing Lined Tunnel with Slip (using liners)'
; Create model geometry
block create tunnel radius 1.0 length 0 5 ...
blocks-radial 4 blocks-tangential 2 blocks-axial 5 radius-ratio 1.1
block join
; assume quarter symmetry
block delete range position-x -5 0
block delete range position-z -5 0
block group 'rock'
block group 'tunnel' range cylinder end-1 0 0 0 end-2 0 5 0 radius 1
block zone generate edgelength 0.125 range position-y 0 2
block zone generate edgelength 0.25 range position-y 2 5
; Name regions of the model
block group 'section1' range position-y 0 1 group 'tunnel'
block group 'section2' range position-y 1 2 group 'tunnel'
block group 'section3' range position-y 2 3 group 'tunnel'
block group 'section4' range position-y 3 4 group 'tunnel'
block group 'section5' range position-y 4 5 group 'tunnel'
block face group 'shotcrete1' range group-intersection 'rock' 'section1'
block face group 'shotcrete2' range group-intersection 'rock' 'section2'
block face group 'shotcrete3' range group-intersection 'rock' 'section3'
; Material model and properties
block zone cmodel assign elastic
block zone property density 2000 bulk 50e6 shear 18e6
; contact properties for excavated blocks
block contact material-table default property stiff-norm 1e8 stiff-shear 1e8
; Initial Conditions
block insitu stress -1e6 -1e6 -1e6 0 0 0
; Boundary Conditions
block gridpoint apply velocity-x 0 range position-x 0.0
block gridpoint apply velocity-y 0 range position-y 0.0
block gridpoint apply velocity-z 0 range position-z 0.0
block gridpoint apply velocity 0 0 0 range union position-x 5.0 ...
position-y 5.0 ...
position-z 5.0
; --- Stage 1: excavate tunnel section 1
block excavate range group 'section1'
model solve convergence 1
model save 'tun1'
;
; --- Stage 2: excavate tunnel section 2
block gridpoint initialize displacement (0,0,0)
block history name 'zdisp' displacement-z position (0,1,1)
block history name 'zvel' velocity-z position (0,1,1)
block excavate range group 'section2'
model save 'tun2-initial'
; --- Solve case with no support
model solve convergence 1
model save 'tun2-nosupport'
; --- Solve case with shotcrete
model restore 'tun2-initial'
structure liner create by-block-face id=1 range group 'shotcrete1'
structure liner cmodel assign elastic
structure liner property young 10.5e9 poisson 0.25 thickness=0.2
structure liner property coupling-stiffness-normal=7.4e10 ...
coupling-stiffness-shear=7.4e10 ...
coupling-cohesion-shear=1e20
model cycle 0
model save 'tun2-temp1'
; --- Specify symmetry conditions for nodes along the 3 symmetry planes
structure node system-local x (1,0,0) y (0,-1,0) range position-x 0
structure node fix system-local range position-x 0
structure node fix velocity-x rotation-y rotation-z range position-x 0
structure node system-local x (0,0,-1) y (0,-1,0) range position-z 0
structure node fix system-local range position-z 0
structure node fix velocity-x rotation-y rotation-z range position-z 0
structure node fix velocity-y rotation-x rotation-z range position-y 0
structure node history name 'znode' displacement-z position 0 1 1
structure liner history name 'ndis' coupling-displacement-normal ...
node 3 component-id=45
model cycle 0
model save 'tun2-temp2'
model solve convergence 1
structure liner recover surface (0,1,0) ; surface-y is circumferential
structure liner recover resultants
model save 'tun2a'
; Repeat excavation with lower stiffnesses (factor of 100)
model restore 'tun2-temp2'
structure liner property coupling-stiffness-normal=7.4e8 ...
coupling-stiffness-shear=7.4e8 ...
coupling-cohesion-shear=1e20
model solve convergence 1
structure liner recover surface (0,1,0) ; surface-y is circumferential
structure liner recover resultants
model save 'tun2a-lowstiff'
; Pursue excavation with larger stiffnesses (reduce cohesion)
model restore 'tun2a'
structure node initialize displacement (0,0,0)
structure liner property coupling-cohesion-shear=0.0
model solve convergence 1
structure liner recover surface (0,1,0) ; surface-y is circumferential
structure liner recover resultants
model save 'tun2b'
; --- Stage 3: excavate tunnel section 3
block excavate range group 'section3'
structure liner create by-block-face id=2 range group 'shotcrete2'
; --- Specify symmetry conditions for nodes along the 3 symmetry planes
structure node system-local x (1,0,0) y (0,-1,0) range position-x 0
structure node fix system-local range position-x 0
structure node fix velocity-x rotation-y rotation-z range position-x 0
structure node system-local x (0,0,-1) y (0,-1,0) range position-z 0
structure node fix system-local range position-z 0
structure node fix velocity-x rotation-y rotation-z range position-z 0
structure node fix velocity-y rotation-x rotation-z range position-y 0
structure liner cmodel assign elastic range id 2
structure liner property young 10.5e9 poisson 0.25 thickness=0.2 range id 2
structure liner property coupling-stiffness-normal=7.4e10 ...
coupling-stiffness-shear=7.4e10 ...
coupling-cohesion-shear=0.0 range id 2
model solve convergence 1
structure liner recover surface (0,1,0) ; surface-y is circumferential
structure liner recover resultants
model save 'tun3'
Endnotes
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
