Falling Wedge
Problem Statement
Note
To view this project in 3DEC, use the menu command . The main data files used are shown at the end of this example. All data files are found in the project.
The stability of a rock wedge in the roof of an excavation is analyzed. This problem takes into account the stabilizing effect of the in-situ stresses, and also shows the influence of joint stiffness.
A roof wedge is created by three joints dipping at 60° and with dip directions of 30°, 150°, and 270°. The height of the wedge is 1 meter. An in-situ state of stress has two principal stresses parallel to the excavation roof (equal to −0.05 MPa); the vertical principal stress is zero.
Analytical Solution
Aclosed-form solution of the support force for stabilization of the wedge in the roof of an excavation was derived by Goodman et al. (1982), and is given by the equation
where:
\(n\) = is the number of faces on the block;
\(_i\) = the index denoting the face of the block;
\(A_0\) = required force to stabilize the wedge;
\(W\) = weight of the wedge;
\(\sigma_{n,i}\) = normal stress acting on the \(i\)th face of the wedge;
\(A_i\) = the area of the face of the wedge;
\(\phi_i\) = the friction angle on the face of the wedge;
\(\alpha_i\) = the complement of the dip angle of the joint which creates the face;
\(k_{si}\) = shear stiffness of the joint;
\(k_{ni}\) = normal stiffness of the joint; and
\(i_i\) = roughness angle of the joint.
For this particular case, where
all joints have the same dip angle,
the initial stress state in the plane parallel to free face of the block is hydrostatic, and
all joints have the same ratio between normal and shear stiffness,
the friction coefficient (equal in all joints) required for stability of the wedge without any support can be expressed from the equation above as follows:
The critical friction coefficient (and friction angle) is calculated using the FISH function _limit, listed in data file “FALL.FIS”. (It is assumed that three joints form a block, and their dip directions are not 120°.)
3DEC Model
The 3DEC model shown in Figure 1 consists of seven rigid blocks. Six of the blocks are fixed, and only the isolated wedge is allowed to move under gravity. The mechanical properties are:
density: \(\rho\) = 2000 kg/m3
joint shear and normal stiffness: \(K_n\) = \(K_s\) = 10 MPa/m
gravity acceleration: \(g\) = 10 m/sec2
The numerical simulation is performed by first fixing all the blocks surrounding the wedge and assigning the in-situ stress state. The friction coefficient is then reduced until failure occurs.
Results and Discussion
The 3DEC simulation yields a 34.402° friction angle (required for stability of the wedge) which is, within five significant digits, the same value as the analytic solution for the critical friction angle. The failure of the wedge is indicated in Figure 1.
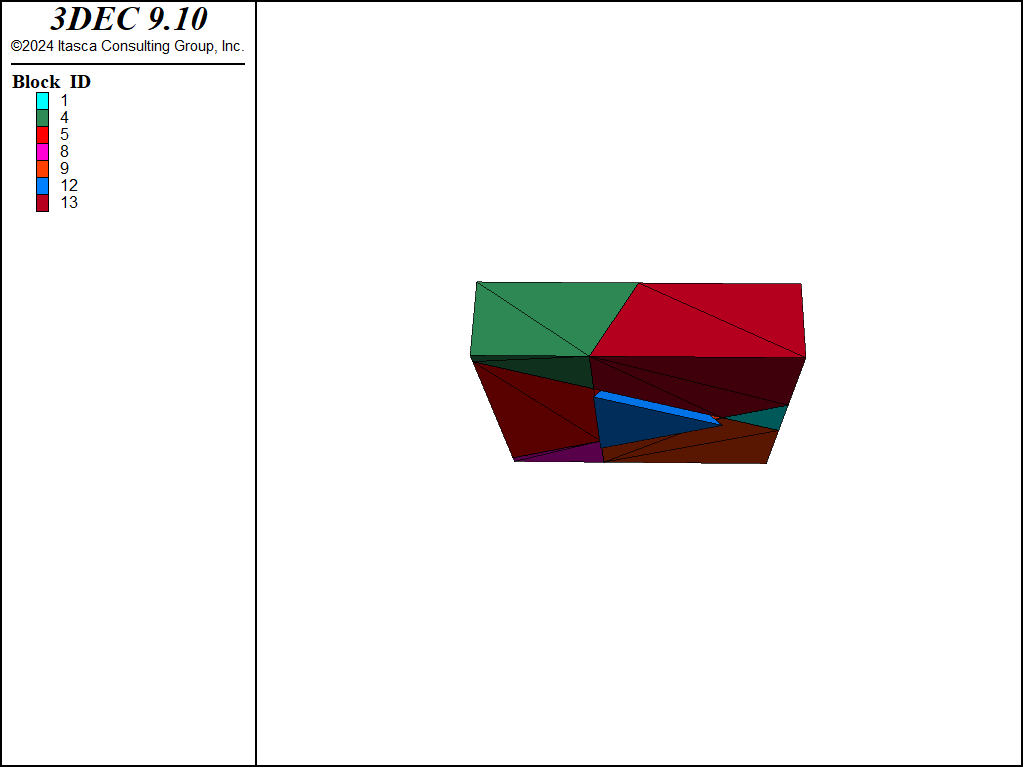
Figure 1: Falling wedge model.
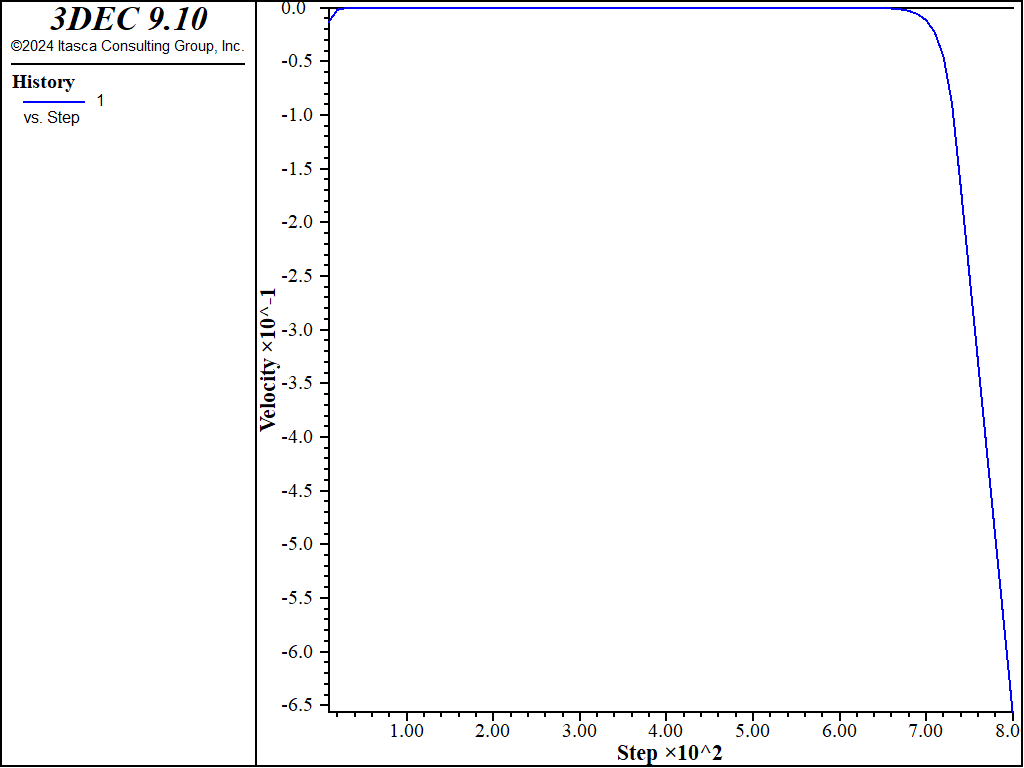
Figure 2: History of vertical velocity of the wedge.
Reference
Goodman, R. E., G.-H. Shi and W. Boyle. “Calculations of Support for Hard, Jointed Rock Using the Keyblock Principal,” in Issues in Rock Mechanics (Proceedings of the 23rd Symposium on Rock Mechanics, University of California, Berkeley, August 1982), pp. 883-898. New York: Society of Mining Engineers (1982).
Data Files
fall.dat
;===================================================
; verification test -- falling wedge
; zero cohesion on the joints, equal friction angle
;===================================================
model new
model large-strain on
program call 'fall.fis'
[_limit]
block create brick -2 2 -2 2 -1 1
block cut joint-set
block cut joint-set dip 60 dip-direction 30 origin 0 0 1
block cut joint-set dip 60 dip-direction 150 origin 0 0 1
block cut joint-set dip 60 dip-direction 270 origin 0 0 1
block delete range position-z -1,0
block group 'wedge' range position-x -0.2,0.2 position-y -0.2,0.2 ...
position-z 0.0,0.3
;
block property density=2e-3
; thistory will create subcontacts
block insitu stress -0.05 -0.05 0 0 0 0
block contact jmodel assign mohr
block contact property stiffness-normal 10 stiffness-shear 10 friction 89
block contact material-table default property stiffness-normal 10 ...
stiffness-shear 10 friction 34.4
model gravity 0 0 -10
block fix range position-x -2.0 2.0 position-y -2.0 2.0 position-z 0.3 1.0
block hide range group 'wedge' not
block history velocity-z position -0.5774,-1,0
history name '1' label 'Z Velocity of Wedge'
block hide off
model cycle 200
; set friction to 34.402
block contact property friction=34.402
model cycle 400
model save 'fall_stable'
; set friction to 34.401
block contact property friction=34.401
model cycle 200
[analytic]
model save 'fall'
program return
fall.fis
fish define params
global height_ = 1.0
global alpha_ = 60.0
global sigma_ = 0.05
global unitweight_ = 0.02
end
[params]
fish define _limit
alpha_ = (90.-alpha_)*math.degrad
local w_ = 0.5*math.sqrt(3)*height_^3* ...
math.tan(alpha_)* ...
math.tan(alpha_)*unitweight_
local a_ = 1.5*math.sqrt(3)*height_^2*math.tan(alpha_)/math.cos(alpha_)
local coef_ = (w_+sigma_*a_*math.sin(alpha_))
coef_ = coef_/(sigma_*a_*math.cos(alpha_)-w_*math.tan(alpha_))
global fang_ = math.atan(coef_)/math.degrad
end
;
fish define analytic
local status = io.out('Analytic solution = '+string(fang_))
end
;
Endnote
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
