FLAC3D Theory and Background • Fluid-Mechanical Interaction
Consolidation Settlement at the Center of a Strip Load (FLAC2D)
Note
To view this project in FLAC2D, use the menu command . Choose “Fluid/ ConsolidationSettlement” and select “ConsolidationSettlement.prj” to load. The project’s main data files are shown at the end of this example.
The prediction of the time settlement of foundations on soft saturated soil is a problem of wide practical interest in soil mechanics. The fluid can in general be considered as incompressible compared to the soil matrix for the simulations, and thus this type of problem is ideal for testing the saturated fast-flow scheme in FLAC3D, described in Fully Saturated Fast Flow. This verification problem involves the consolidation settlement produced by a uniform strip loading on a semi-infinite elastic medium, which is free to drain at the surface.
The two-dimensional poro-elastic problem of a semi-infinite stratum loaded on the plane \(z\) = 10 by a uniform normal pressure, \(P\), along the strip \(-a \le x \le a\) has been analyzed by McNamee and Gibson (1960). The fluid is assumed to be incompressible in their solution. The case in which the pore pressure vanishes at \(z\) = 10 (i.e., a completely permeable surface) is considered. The consolidation surface settlement for the special case of zero Poisson’s ratio is given by the closed form solution
where
\(\hat{u}\) and \(\hat{u}_{und}\) are the nondimensional total vertical displacement and undrained vertical displacement, respectively, at \(z\) = 0. \(\hat{x}\) is the nondimensional horizontal distance, and \(\hat{G}\) is the nondimensional shear modulus. These quantities are defined:
where \(u_z\) is the vertical displacement, and \(G\) is the shear modulus.
erf is the error function and \(E_1\) is the exponential integral. \(\tau\) is a dimensionless time parameter, given as
where \(c_v\) is the scaled diffusivity, and \(t\) is time. For zero Poisson’s ratio, \(c_v\) is defined as
where \(k\) is the mobility coefficient.
For the numerical simulation with FLAC2D, \(a\) = 1, \(\hat{G}\) = 0.5, \(P\) = 1, and \(c_v\) = 1. Advantage is taken of the problem geometry half-symmetry.
The FLAC2D model grid used for this analysis is shown in Figure 1.
The grid has dimensions of 10 by 10, and a total of 1287 zones. The origin of the reference axes is
located at the strip centerline. The isotropic elastic material model
is used with the shear modulus equal to 0.5 and Poisson’s ratio equal to 0. Roller boundaries are
specified along the symmetry and bottom boundaries. The right boundary is fixed in both directions.
The simulation is run using the fluid configuration (model configure fluid-flow) with an initial saturation of 1
throughout the model. Pore pressure is fixed at zero at the surface of the model (\(y\) = 10) to model
free draining conditions.
Figure 1: FLAC3D grid.
A uniform mechanical pressure of \(P\) = 1 is applied along the strip location to simulate the strip
loading. The fastflow option (zone fluid fastflow on) is selected. The undrained response
is calculated first (with model solve-static)
Displacements are then reset to zero, and a coupled fluid-mechanical simulation is performed (using
:cmd:`model solve-fluid-copuled) for a period of 8 time units.
The predicted time history of the surface settlement at the center of the strip is compared to the analytical value in Figure 2. The difference between results over the course of the simulation is less than 1%.
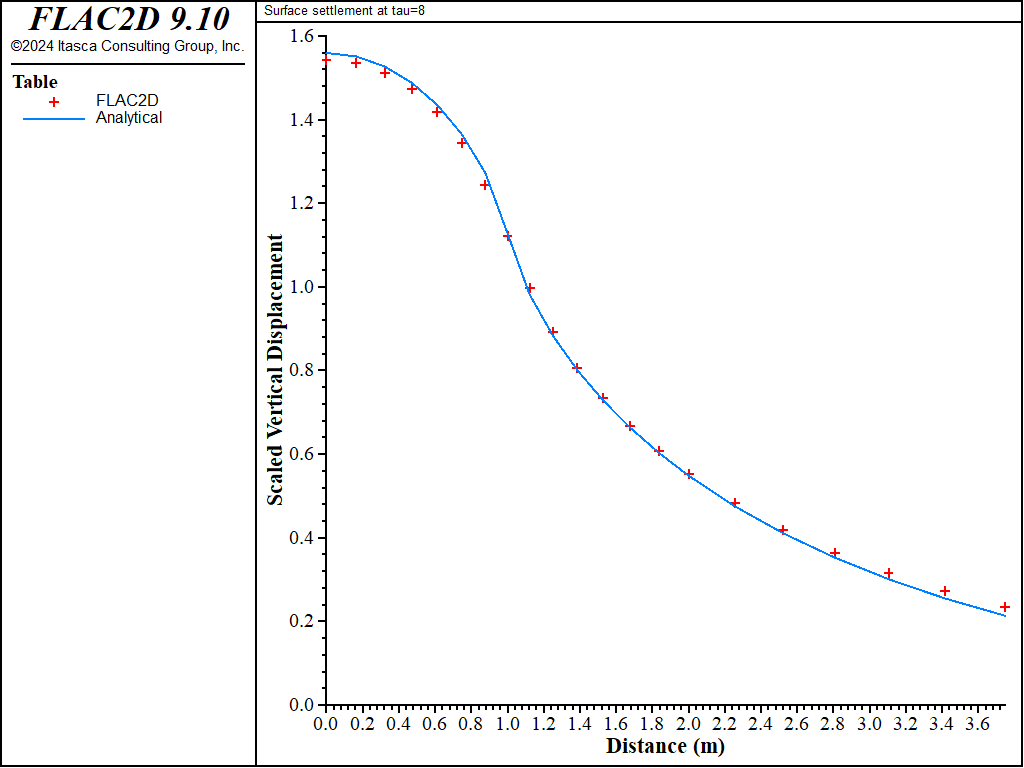
Figure 2: Consolidation settlement (\({\hat{u}-\hat{u}_{und}}\)) at the center of the strip versus log(\(\tau\)) — comparison between FLAC3D and analytical solutions.
The surface consolidation settlement calculated by FLAC2D at the end of the simulation (\(\tau\) = 8) is compared to the analytical solution in Figure 3. The results are in good agreement. The discrepancy observed away from the strip location is attributed to boundary effects. This discrepancy can be reduced by increasing the model lateral and vertical extents.
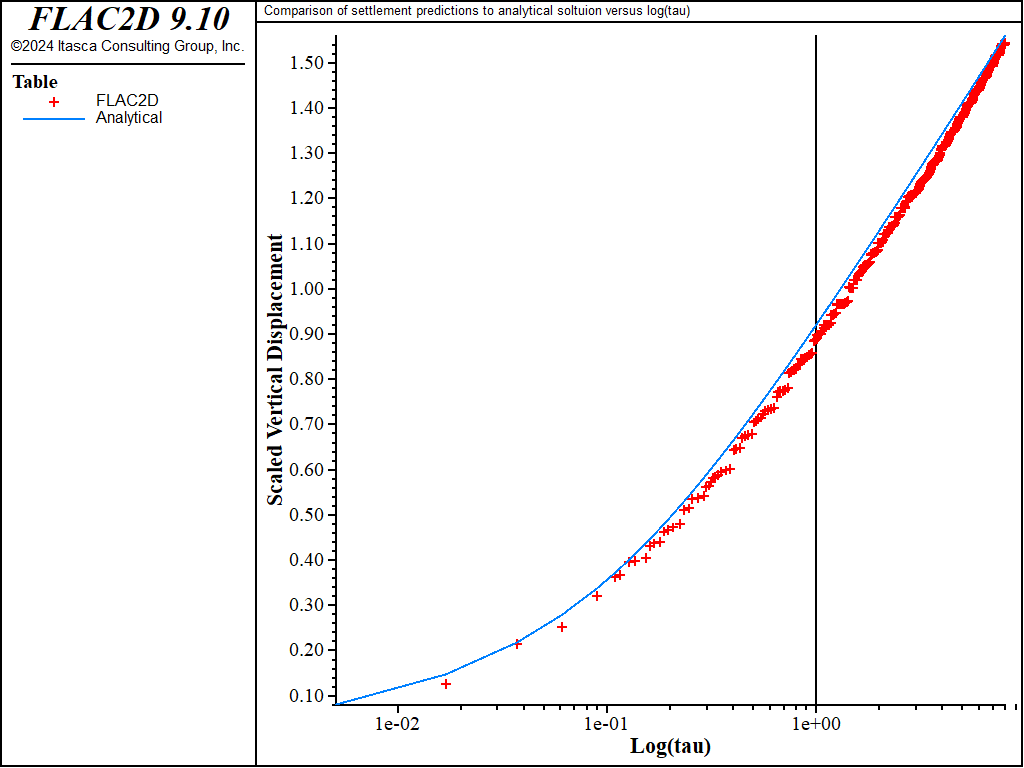
Figure 3: Surface settlement profile at \(\tau\) = 8 — comparison between FLAC3D and analytical solutions.
The predicted excess pore pressure at \(\hat{x}\) = 0, \(\hat{y}\) = 0, \(\hat{z}\) = 9.5, scaled by the undrained pore pressure value, is plotted versus log(\(\tau\)) in Figure 4. The FLAC2D results are compared to the reference solution obtained by Schiffman et al. (1969) and reported by Burghinoli et al. (2001).
An interesting observation is that pore pressure rises initially above the initial undrained value before decaying to zero. This behavior is typical of the Mandel-Cryer effect (Cryer 1963). The peak pressure is slightly different by the FLAC2D solution, but a fair agreement is obtained at later times.
Displacement contours at \(\tau\) = 8 are shown in Figure 5.
break
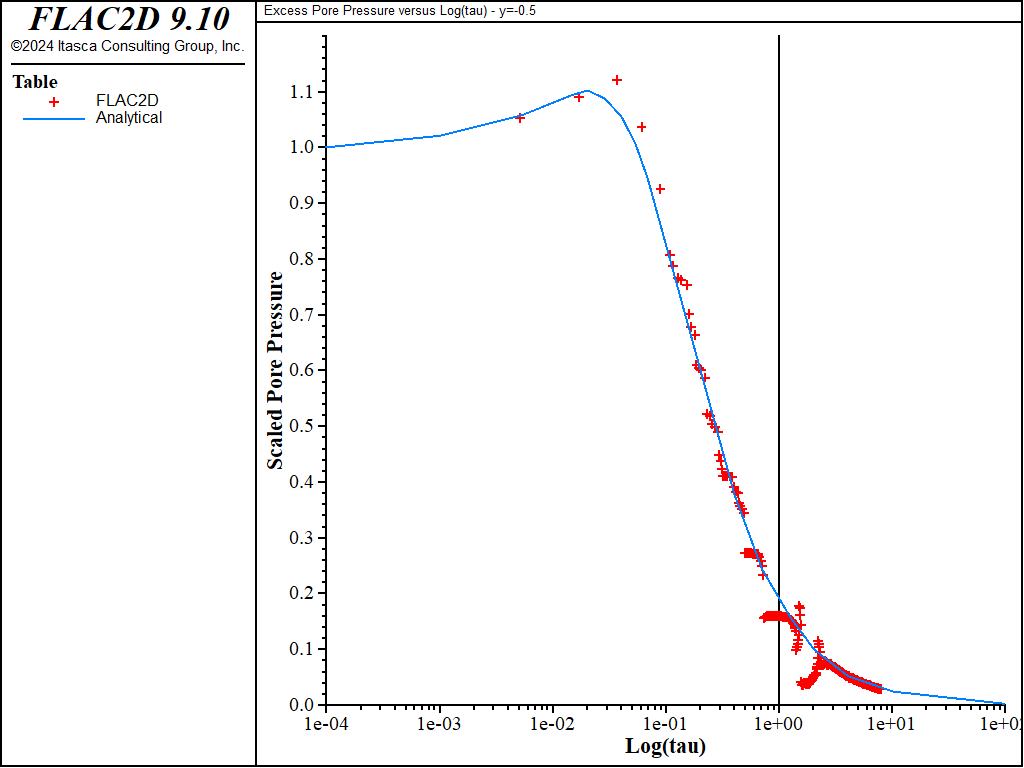
Figure 4: Scaled excess pore pressure at \(\hat{z}\) = -0.5 versus log(\(\tau\)) — comparison between FLAC3D and reference solution given by Schiffman et al. (1969).
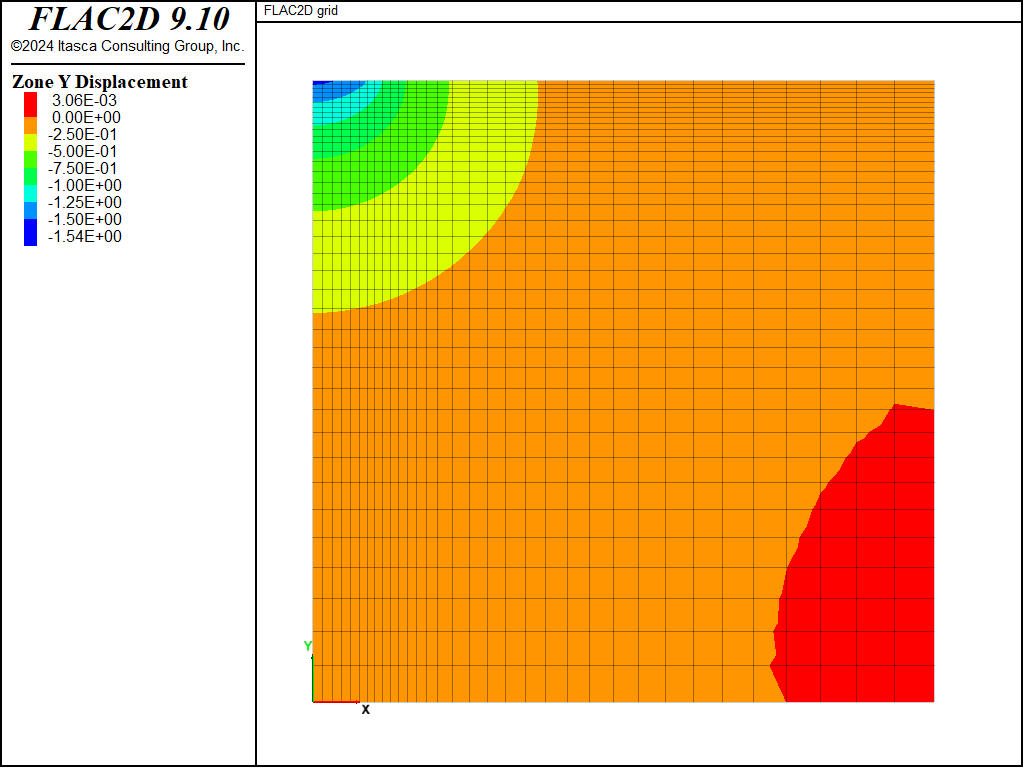
Figure 5: Displacement contours at \(\tau\) = 8.
References
Burghinoli, A., S. Miliziano and F. M. Soccodato. “Effectiveness of the fast-flow algorithm: 2D consolidation benchmark and tunneling application,” FLAC and Numerical Modeling in Geomechanics — 2001 (Proceedings of the 2nd International FLAC Symposium, Lyon, France, October 29 - 31, 2001), pp. 345 - 352. D. Billaux et al., eds. Swets & Zeitlinger (2001).
Cryer, C. W. “A Comparison of the Three-Dimensional Consolidation Theories of Biot and Terzaghi,” Quart. J. Mech. and Appl. Math., XVI, 4, 401-412 (1963).
McNamee, J., and R. E. Gibson. “Plane strain and axially symmetric problems of the consolidation of a semi-infinite clay stratum,” Quart. J. Mech. and Appl. Math. XIII, Pt. 2, (1960).
Schiffman, R. L., A. Chen and J. C. Jordan. “An Analysis of Consolidation Theories,” J. Soil Mech. and Found. Div., ASCE, 95(SM1), 285-312 (1969).
break
Data File
ConsolidationSettlement.dat
model new
model title "Strip load on semi-infinite elastic medium"
; Model geometry
program call 'geometry' ; Created using the 2D Sketch interactively
zone generate from-sketch
zone face skin
zone gridpoint group 'output' range position (0,10) (4,10)
; --- mechanical model ---
model large-strain off
zone cmodel assign elastic
zone property bulk=[1.0/3.0] shear=0.5
; --- boundary conditions ---
zone face apply velocity-normal 0 range group 'West' or 'Bottom'
zone face apply velocity (0,0) range group 'East'
; --- apply load slowly ---
zone ratio convergence
zone face apply stress-normal -1 servo ramp lower-bound 4e-2 ...
range position-x 0 1 group 'Top'
; --- fluid flow model ---
model configure fluid-flow
zone fluid property mobility-coefficient=1.0 porosity 0.3
; --- pore pressure fixed at zero at the surface ---
zone face apply pore-pressure 0 range group 'Top'
; --- settings ---
zone fluid fastflow on
; --- undrained response ---
model solve-static convergence 0.1
model save 'undrained'
; --- consolidation settlement ---
zone gridpoint initialize displacement (0,0)
;
zone history name 'ydisp' displacement-y position (0,10)
zone history name 'pp' pore-pressure position (0,9.5)
model history name 'ftime' fluid time-total
;
zone fluid timestep fix 1e-4
history interval 50
model solve-fluid-coupled time 0.1 convergence 40
model fluid timestep automatic
history interval 20
model solve-fluid-coupled time 7.9 convergence 40
model save 'strip8'
program return
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
