Transient Thermal Response of Sheet with Constant Temperature Boundaries
Note
The project file for this example may be viewed/run in PFC. The data files used are shown at the end of this example.
A planar sheet of width \(L\) is initially at a uniform temperature of 0°C. The left side of the sheet is exposed to a constant temperature of 100°C, while the right side is kept at 0°C. The sheet eventually reaches an equilibrium state at a constant heat flux and unchanging temperature distribution. The analytical solution for temperature within the sheet as a function of distance from the left side, \(x\), and time, \(t\), is given by [Crank1975]
where \(T_1\) is the temperature at the left side of the sheet (equal to 100°C), and \(\kappa\) is the thermal diffusivity given by
where \(k\) is the thermal conductivity, \(\rho_t\) is the material density, and \(C_v\) is the specific heat at constant volume.
Numerical Model
This thermal problem is one-dimensional and can be modeled as a thin slice of material with constant temperatures applied to its left and right boundaries and adiabatic conditions on the upper and lower boundaries to represent thermal symmetry planes.
For this example, we create two different PFC2D models consisting of a cubic packing and a hexagonal packing (see Figures 1 and 2). For these two uniform packings, the porosity and the thermal resistance can be expressed analytically. The porosity is given by [Deresiewicz1958b]:
The thermal resistance is found by applying Equation (28) of the PFC Thermal Formulation section to a control volume that surrounds one particle, and noting that the length of each thermal pipe contained within the control volume equals the particle radius, \(R\), to yield
where \(t\) is the disk thickness (equal to unity in this case). The data file used to perform the simulation is “transient_sheet.dat“. It makes use of FISH functions defined in “transient_sheet-utils.p2fis“. Thermal properties and boundary conditions are specified, and then each model is run for 50 and 200 cycles, until the thermal equilibrium state is reached (using the model solve command). The normalized temperature distributions at the increasing thermal times for the cubic- and hexagonal-packed specimens are plotted along with the analytical solutions in Figures 3 and 4. There is a good match between the PFC2D responses and the analytical solutions.

Figure 1: Contour of ball temperature and thermal power vector field (PFC2D cubic pack).
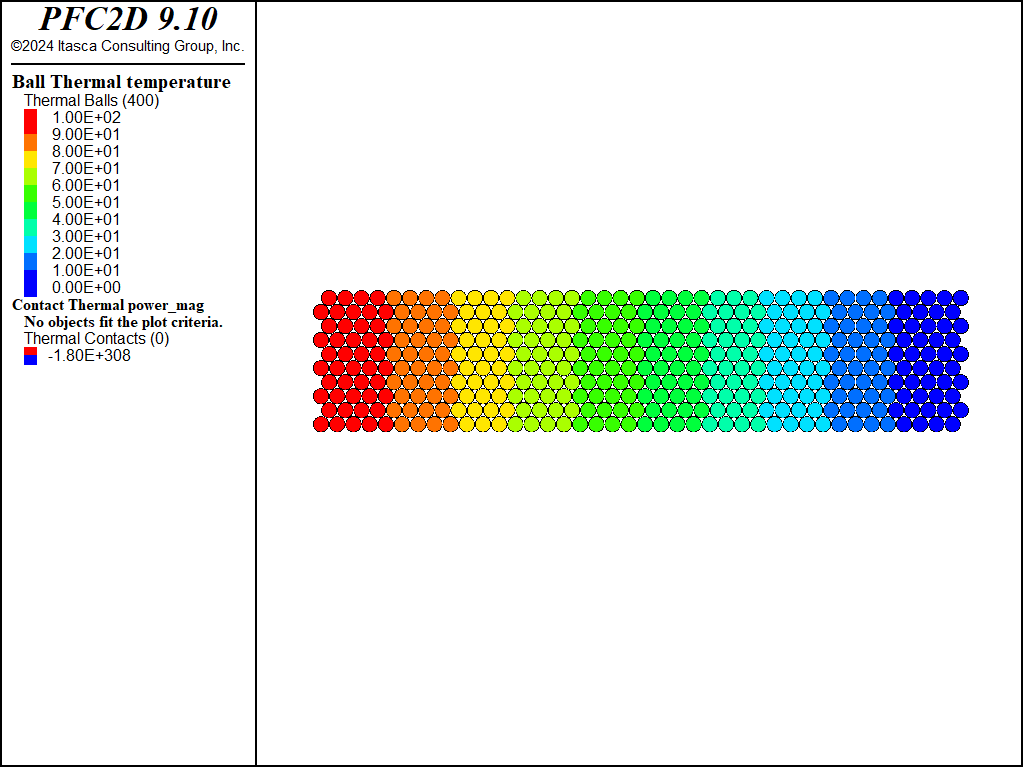
Figure 2: Contour of ball temperature and thermal power vector field (hexagonal pack).
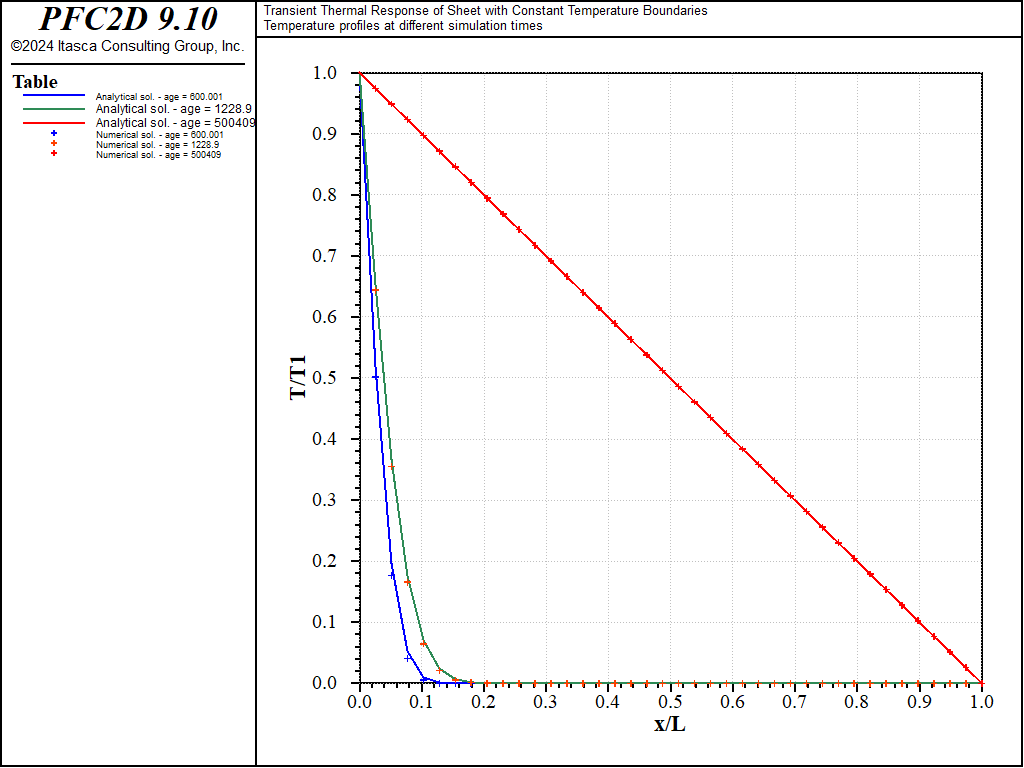
Figure 3: Modeled and analytical normalized temperature distributions for increasing thermal time (cubic pack).
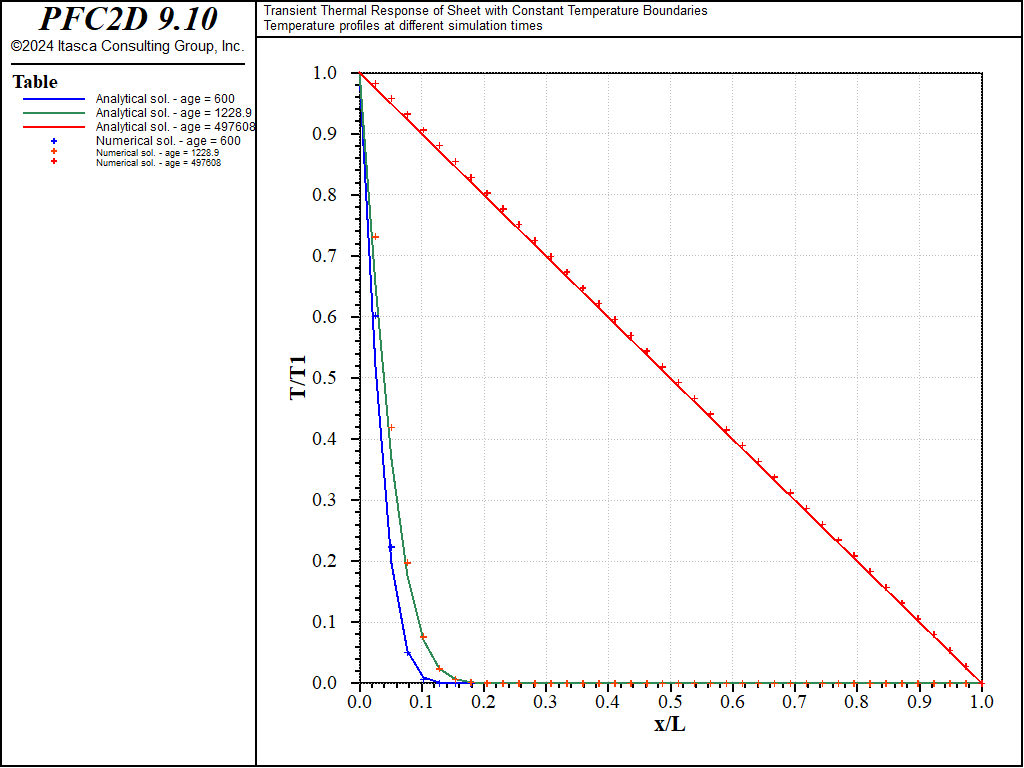
Figure 4: Modeled and analytical normalized temperature distributions for increasing thermal time (hexagonal pack).
References
Crank, J. The Mathematics of Diffusion, 2nd Ed. Oxford: Oxford University Press, 1975.
Deresiewicz, H. “Mechanics of Granular Matter,” in Advances in Applied Mechanics, Vol. 5, pp. 233-306. H. L. Dryden and Th. von Karman, eds. New York: Academic Press, 1958.
Data Files
transient_sheet.dat
; fname: transient_sheet.dat (2D)
;
; Itasca Consulting Group, Inc.
; ========================================================================
; Thermal option example :
; TRANSIENT RESPONSE OF SEMI-INFINITE SOLID WITH APPLIED HEAT FLUX
; (CUBIC AND HEXAGONAL PACKINGS)
;
; ========================================================================
program log-file 'transient_sheet.log'
program log on
; ========================================================================
model new
model large-strain on
model configure thermal
model mechanical off thermal on
program echo off
program call 'transient_sheet-utils.p2fis'
program echo on
[global t1 = 'Transient Thermal Response of Sheet']
[global t2 = ' with Constant Temperature Boundaries']
model title [t1 + t2]
[init_params]
model save 'transient_sheet-ini'
[n_row = 10]
[n_col = 40]
[_pack_type = 1]
[close_pack(n_row,n_col,_pack_type)]
;
model solve thermal time-total 600.0
[num_soln]
[ana_soln]
model solve thermal time-total 1200.0
[num_soln]
[ana_soln]
model solve thermal unbalanced-maximum 1e-3
[num_soln]
[ana_soln]
;
model save 'transient_sheet-cubic'
model restore 'transient_sheet-ini'
[n_row = 10]
[n_col = 40]
[_pack_type = 2]
[close_pack(n_row,n_col,_pack_type)]
model thermal timestep maximum 1.0e2
model solve thermal time-total 600.0
[num_soln]
[ana_soln]
model solve thermal time-total 1200.0
[num_soln]
[ana_soln]
model solve thermal unbalanced-maximum 1e-3
[num_soln]
[ana_soln]
;
model save 'transient_sheet-hexa'
; ========================================================================
program log off
program return
;EOF: transient_sheet.dat (2D)
transient_sheet-utils.p2fis
;fname: transient_sheet-utils.p2fis
;
; Itasca Consulting Group, Inc.
; ============================================================================
; Utility functions for thermal option verification problems
; ============================================================================
;
; ----------------------------------------------------------------------------
fish define init_params
global id_start=1
global x0 = 0.0
global y0 = 0.0
global radius = 1.0
global epsilon = 1.0e-6
;
global c_k = 1.6 ; conductivity
global c_cv = 0.2 ; specific heat
global c_dens = 1000.0 ; density
global c_kappa = c_k / (c_dens*c_cv)
global t1 = 100.0 ; temperature along left side
global tabn_start = 10
global tabe_start = 11
global tabn = tabn_start
global tabe = tabe_start
global n_row = 10
global n_col = 50
global _pack_type = 1
global n_tot = 100 ; number of terms of analytical solution to use
global final_params
global therm_props
global therm_bcs
end
; ----------------------------------------------------------------------------
fish define close_pack(nrow_,ncol_,type_)
global xc = x0
global yc = y0
global rc = radius
global idc = id_start
local r2 = 2.0 * rc
global dom_xmin = x0 - 4.0 *r2
global dom_xmax = x0 + ncol_*r2 + 4.0 *r2
global dom_ymin = y0 - 4.0 *r2
global dom_ymax = y0 + nrow_*r2 + 4.0 *r2
command
model domain extent [dom_xmin] [dom_xmax] [dom_ymin] [dom_ymax]
endcommand
case_of type_
case 1
yinc = radius * 2.0
case 2
yinc = radius * math.sqrt(3.0)
end_case
loop local row (1,nrow_)
loop local col (1,ncol_)
command
ball create id=[idc] position-x=[xc] position-y=[yc] ...
radius=[rc*(1 + epsilon)]
end_command
idc = idc + 1
xc = xc + r2
end_loop
yc = yc + yinc
case_of type_
case 1
xc = x0
case 2
xc = x0 + radius * (row - (row//2) * 2)
end_case
end_loop
final_params
therm_props
therm_bcs
end
; ----------------------------------------------------------------------------
fish define final_params
global c_len = (n_col-1)*2.0*radius
end
; ----------------------------------------------------------------------------
fish define therm_props
;
if _pack_type = 1 then
poros = 1.0 - (math.pi/4.0)
_eta = 1.0 / (2.0 * c_k * radius)
else
poros = 1.0 - math.pi/(2.0*math.sqrt(3.0))
_eta = 3.0 / (2.0*math.sqrt(3.0) * c_k * radius)
end_if
_dens = c_dens / (1.0 - poros)
command
contact cmat default model Linear
contact cmat thermal default model ThermalPipe property thres=[_eta]
contact cmat thermal default inheritance thres off
ball attribute density=[_dens]
ball thermal attribute specific-heat=[c_cv]
model clean
end_command
end
; ----------------------------------------------------------------------------
fish define therm_bcs
;
global _xl1 = -0.01*radius
global _xr1 = _xl1 + 1.01*radius
global _xl2 = c_len - 0.01*radius
global _xr2 = _xl2 + 1.01*radius
command
ball thermal attribute temperature 0.0
ball thermal attribute temperature [t1] range position-x=([_xl1], [_xr1]) ; left side
ball thermal fix range position-x=([_xl1], [_xr1]) ; left side
ball thermal fix range position-x=([_xl2], [_xr2]) ; right side
end_command
end
; ----------------------------------------------------------------------------
fish define num_soln
;
; ----- Numerical solution (along bottom row of balls)
global tname = string.build("Numerical sol. - age = %1",thermal.time.total)
local t = table.create(tabe)
table.label(t) = tname
tabe +=2
loop foreach local btp ball.thermal.list
local bp = ball.thermal.ball(btp)
if ball.pos(bp,2) = 0.0 then
local _z = ball.pos(bp,1)
local _tz = _z / c_len
table(t, _tz) = ball.thermal.temp(btp) / t1
end_if
end_loop
end
; ----------------------------------------------------------------------------
fish define ana_soln
;
; ----- Analytical solution (along bottom row of balls).
; Do not test for convergence, just take the first [n_tot] terms.
global tname = string.build("Analytical sol. - age = %1",thermal.time.total)
local t = table.create(tabn)
table.label(t) = tname
tabn +=2
loop foreach local btp ball.thermal.list
local bp = ball.thermal.ball(btp)
if ball.pos(bp,2) = 0.0 then
local _z = ball.pos(bp,1)
local n = 0
local tsum = 0.0
loop while n < n_tot
n = n + 1
fn = float(n)
local term = math.sin(math.pi*_z*fn/c_len)
term = term * math.exp(-c_kappa*fn*fn*math.pi*math.pi* ...
thermal.time.total/(c_len*c_len))/fn
tsum = tsum + term
end_loop
_tz = _z / c_len
table(t, _tz) = 1.0 - _z/c_len - (2.0/math.pi)*tsum
end_if
end_loop
end
; ----------------------------------------------------------------------------
fish define init_params
global id_start=1
global x0 = 0.0
global y0 = 0.0
global radius = 1.0
global epsilon = 1.0e-6
;
global c_k = 1.6 ; conductivity
global c_cv = 0.2 ; specific heat
global c_dens = 1000.0 ; density
global c_kappa = c_k / (c_dens*c_cv)
global t1 = 100.0 ; temperature along left side
global tabn_start = 10
global tabe_start = 11
global tabn = tabn_start
global tabe = tabe_start
global n_row = 10
global n_col = 50
global _pack_type = 1
global n_tot = 100 ; number of terms of analytical solution to use
end
; ============================================================================
;EOF: transient_sheet-utils.p2fis
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
