Heated Specimen with Free Boundaries
Note
The project file for this example may be viewed/run in PFC. The data files used are shown at the end of this example.
A temperature change, \(\Delta T\), is applied to a cubic specimen with unconstrained boundaries. The thermally induced strains are measured and compared with analytical values for an isotropic elastic continuum.
Analytical Values
The stress-strain relation with thermally induced strain is given by Equation (1) ([Timoshenko1970b]):
where \(E\) and \(\nu\) are the Young’s modulus and the Poisson’s ratio, respectively. Also, \(\alpha_t\) is the coefficient of linear thermal expansion.
The analytical values for the thermally induced strains with free boundaries are given by Equation (2):
Model and Results
The file “free_expansion.dat” is used for this example. A 2 × 2 × 2 m specimen is created. It comprises approximately 4000 balls with uniform size distribution (radius range from 0.05 to 0.08 m), with a porosity of 0.36. Once the specimen is generated, contact bonds are installed at ball-ball contacts, the surrounding walls are deleted, and the specimen is brought to equilibrium.
The strains are measured using a measurement sphere with a radius of 0.95 m, centered within the specimen. In PFC, the particle thermal-expansion coefficient is the same as the coefficient of linear thermal expansion: \(\alpha_t\) = 3 × 10-6/°C, in this case.
The expected strains for \(\Delta T\) = +100°C are
The expected strains for \(\Delta T\) = -100°C are
Figure 1 and Figure 2 show displacement vectors resulting from the positive and negative temperature change; they show an isotropic expansion and isotropic contraction, respectively. Figure 3 and Figure 4 show histories of strain recorded during the expansion and contraction phases respectively.
The result of the simulation is in accordance with the analytical solution.

Figure 1: Displacement field at the end of thermal isotropic expansion.

Figure 2: Displacement field at the end of thermal isotropic contraction.
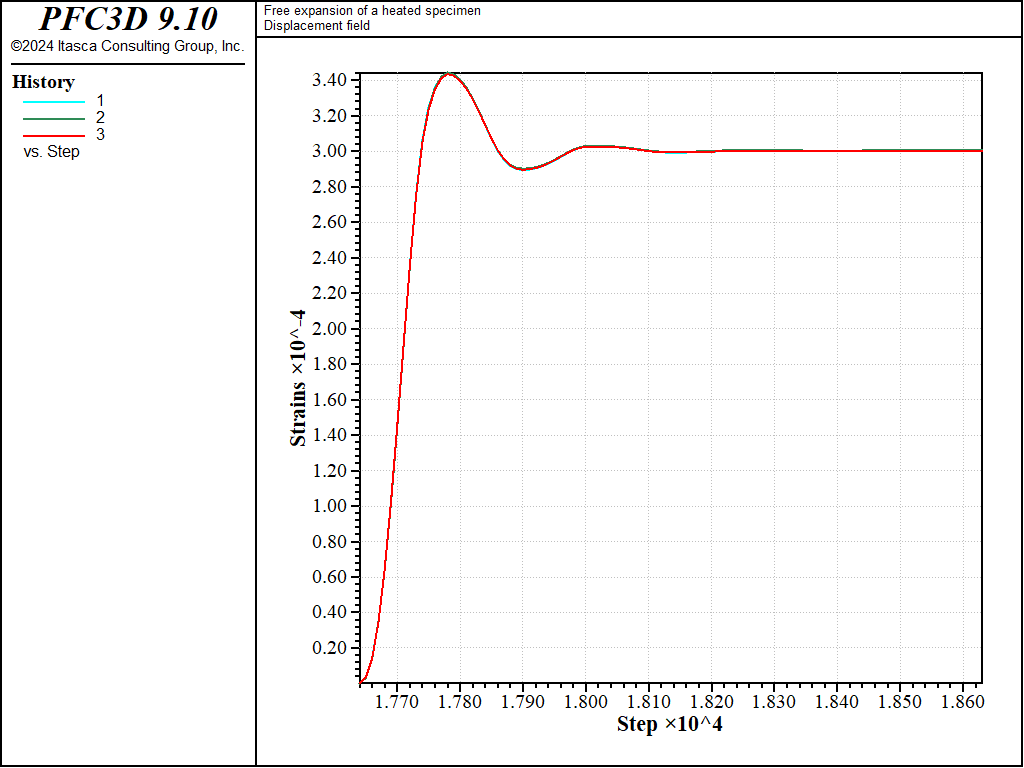
Figure 3: Strain histories at the end of thermal isotropic expansion.
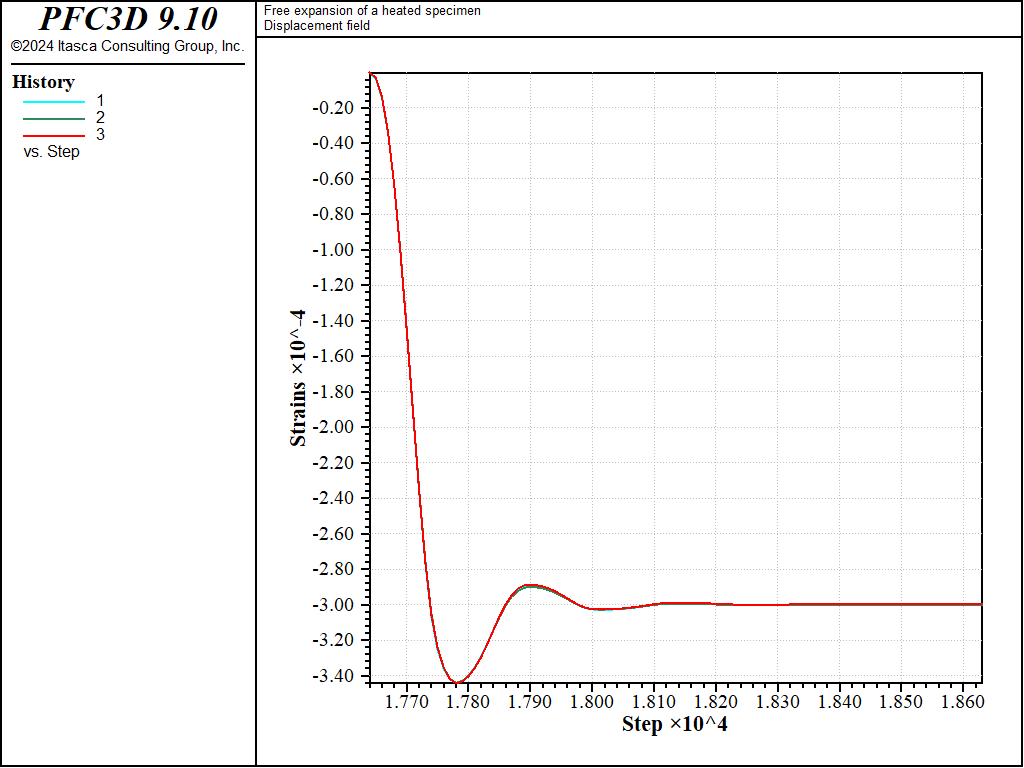
Figure 4: Strain histories at the end of thermal isotropic contraction.
References
Timoshenko, S. P., and J. N. Goodier. Theory of Elasticity, 3rd Ed. New York: McGraw-Hill, 1970.
Data Files
free_expansion.dat
; fname: free_expansion.dat (3D)
;
; Itasca Consulting Group, Inc.
; ========================================================================
; Thermal option verification problem:
; Free expansion of a heated specimen
;
; ========================================================================
program log-file "free_expansion.log"
program log on
; ========================================================================
model new
model large-strain on
model title 'Free expansion of a heated specimen'
; build specimen
model domain extent -5 5
*contact cmat default type ball-ball ...
model linearcbond ...
method deformability emod 3.81e8 kratio 1.0 proximity 0.005
contact cmat default type ball-facet ...
model linear ...
method deformability emod 3.81e8 kratio 1.0
wall generate box -1 1
model random 10001
ball distribute porosity 0.36 ...
radius 0.05 0.08 ...
box -1 1
ball attribute position multiply 0.95
ball attribute density 1500.0 damp 0.7
model cycle 2000 calm 100
model mechanical timestep scale
model solve ratio-average 1e-4
contact method bond gap 0.005
contact property cb_tenF 1e20 cb_shearF 1e20
wall delete
ball attribute displacement multiply 0.0
model cycle 1000
model mechanical timestep automatic
model solve ratio-average 1e-6
; install measurement sphere and activate strain calculation
measure create id 1 radius 0.95
fish define ini_mstrains
global mp = measure.find(1)
global mstrains = matrix(3,3)
end
[ini_mstrains]
fish define accumulate_mstrains
global msrate = measure.strain.rate(mp)
global mstrains = mstrains + msrate * global.timestep
global xxmstrain = mstrains(1,1)
global yymstrain = mstrains(2,2)
global zzmstrain = mstrains(3,3)
end
fish callback add accumulate_mstrains 11.0
fish history xxmstrain
fish history yymstrain
fish history zzmstrain
model save "initial"
;---------------- case a: apply +100 deg C ----------------------------
model configure thermal
ball thermal attribute expansion 3.0e-6
ball thermal attribute specific-heat 1.0e3
ball thermal attribute temperature 0.0
ball thermal attribute temperature-increment=100.0
model cycle 1
model thermal off mechanical on
ball attribute displacement multiply 0.0
model cycle 1000
model solve ratio-average 1e-6
model save "final1"
;---------------- case b: apply -100 deg C ----------------------------
model restore "initial"
model configure thermal
ball thermal attribute expansion 3.0e-6
ball thermal attribute specific-heat 1.0e3
ball thermal attribute temperature 0.0
ball thermal attribute temperature-increment=-100.0
model thermal on mechanical on
model cycle 1
model thermal off mechanical on
ball attribute displacement multiply 0.0
model cycle 1000
model solve ratio-average 1e-6
model save "final2"
program log off
program return
; ========================================================================
; eof: free_expansion.dat (3D)
⇐ Transient Thermal Response of Sheet with Constant Temperature Boundaries | Heated Specimen with Fixed Boundaries ⇒
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
