Embankment Loading on a Cam-Clay Foundation (FLAC3D)

Problem Statement

Note

The project file for this example is available to be viewed/run in FLAC3D.[1] The project’s main data file is shown at the end of this example.

The response of a saturated soil foundation to loading by a long embankment is studied in this example. The analysis is carried out for a slice of soil foundation of unit thickness normal to the embankment axis. The foundation is 10 meters deep, and the groundwater free surface is at the ground level. The embankment is 8 meters wide. The soil behavior corresponds to a Cam-clay material. The initial stress and pore pressure states correspond to equilibrium under gravity with a ratio of horizontal to vertical effective stress of 6/13. The weight of the embankment is simulated by an applied surcharge and drainage occurs at the soil surface.

The soil has several properties, which are listed in Table 1.

Table 1: Soil Properties

drained Poisson’s ratio (\(ν\))	0.3
soil constant (\(M\))	0.888
slope of normal consolidation line (\(λ\))	0.161
slope of elastic swelling line (\(κ\))	0.062
reference pressure (\(p_1\))	100.0 Pa
specific volume at reference pressure (\(v_λ\))	2.858
porosity	0.3
dry density (\(ρ\))	2 × 103 kg/m3

The clay is lightly over-consolidated, and the initial value of the cap pressure, \(p_c\), is equal to 1.6 × 10⁵ Pa in the example. (Note that for a normally consolidated soil, the value for \(p_c\) is equal to 1.579 × 10⁵ Pa at the base of the clay layer, where \(p\) = 8.33 × 10⁴ Pa and \(q\) = 7.0 × 10⁴ Pa.) The drained Poisson’s ratio of the material is assumed to remain constant during the simulation.

The foundation has a permeability, \(k\), of 10^-12 (m/s)/(Pa/m). The soil moduli are functions of the mean effective pressure and the soil-specific volume, quantities that vary in space and evolve during the simulation. The average value of \(K + 4/3 G\), however, stays of the order of 10⁶ Pa, or two orders of magnitude lower than the water bulk modulus (\(K_w\) is 2 × 10⁸ Pa). The diffusivity, \(c\), is thus controlled by the soil material in this example. Its magnitude can be estimated from the formula \(c = k(K + 4/3 G)\), and is of the order of 10^-6 m²/s. The time scale for the diffusion process can be estimated using \(t_c\) = \(L\)²/\(c\), where \(L\) is the model height. Using \(L\) = 10 m, we have that \(t_c\) is of the order of three years. Compared to that time, construction of the embankment may be assumed to occur instantaneously. An undrained analysis is first conducted to evaluate the foundation settlement in the short-term after building of the embankment; the long-term response is then monitored after allowing drainage from the soil surface.

Modeling Procedure

The model, represented in Figure 1, takes advantage of half-symmetry. The size is 20 meters wide and 10 meters deep. Note that the width of the model is not necessarily large enough to accurately represent an extensive soil layer; the model is intended for illustrative purposes only. The mechanical boundary conditions correspond to roller boundaries on both sides of the plane of analysis (\(y\)-direction), roller boundaries along the symmetry line and the far boundary of the model (\(x\)-direction), and to fixed displacements in the \(x\)-, \(y\)-, and \(z\)-direction at the model base. The maximum bulk modulus of the clay (bulk-maximum) is set to 5 × 10⁶ Pa, a value that is approximately twice the initial value of the actual bulk modulus (bulk) at the bottom of the clay layer.

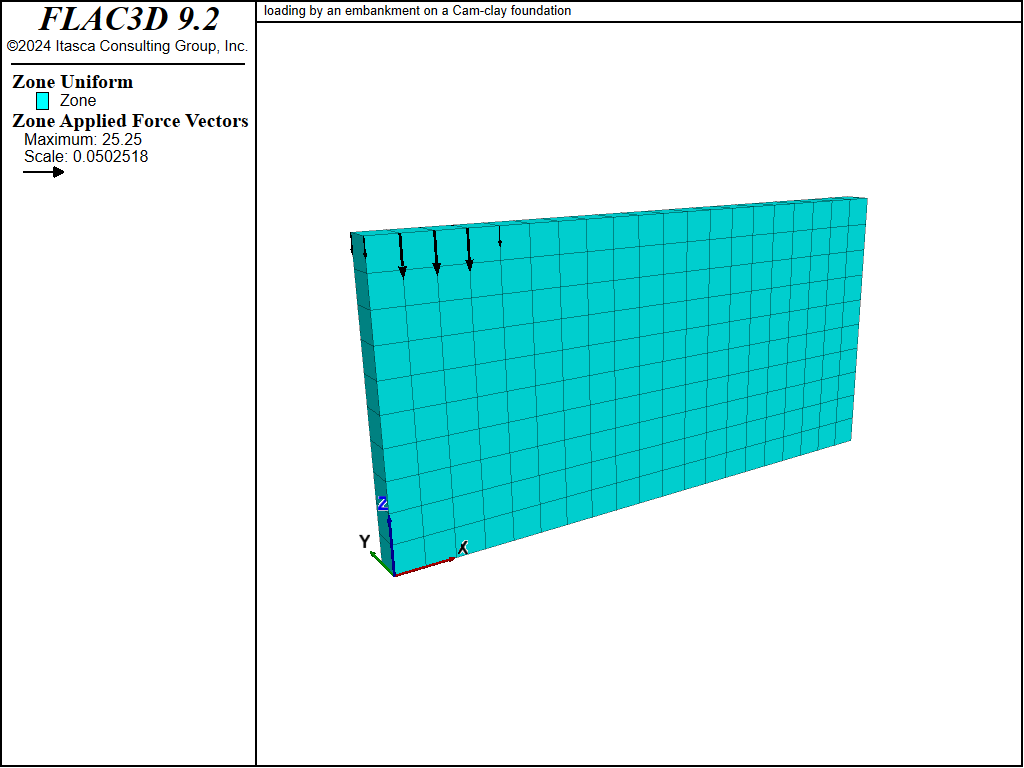
Figure 1: Model geometry.

The first stage of the simulation corresponds to the short time response of the system in which no flow is assumed to take place. The command model fluid active off is specified. Loading by the embankment is simulated by progressive application of a pressure of 50 kPa on a 4 meter section of the model top boundary (to reproduce proportional loading conditions). Once the full load is attained, the model is cycled to equilibrium. During this stage, pore pressures develop as a result of volumetric deformations, but do not dissipate.

In the second stage, fluid flow is allowed to develop by issuing the command model fluid active on. Water then drains through the top of the model where the pore pressure is fixed at zero, and additional settlement takes place under the embankment. The model solve fluid time-total command, used to perform the coupled simulation, requires parameters that determine the accuracy of the solution. These parameters may need to be adjusted if different properties or model conditions are used. Refer to Coupled Flow and Mechanical Calculations for a discussion on these topics. Stresses, pore pressures, and vertical displacements are monitored during the calculation. The data file for this problem is listed in the end of this page.

Results and Discussion

Displacement vectors, vertical displacement contours, and the pore pressure distribution at the end of the undrained and drained numerical simulations are presented in Figure 2 to Figure 7. The vertical displacement histories in Figure 8, recorded at four monitoring points, indicate that the maximum settlement under the embankment increases from approximately 0.14 m to 0.19 m as a result of drainage. Note that the displacement vectors in Figure 3 and vertical displacement contours in Figure 5 correspond to the combined undrained and drained displacements.

In Figure 9, the graph of pore pressure evolution at two monitoring points confirms that a steady-state flow has been reached by the end of the drained simulation.

break

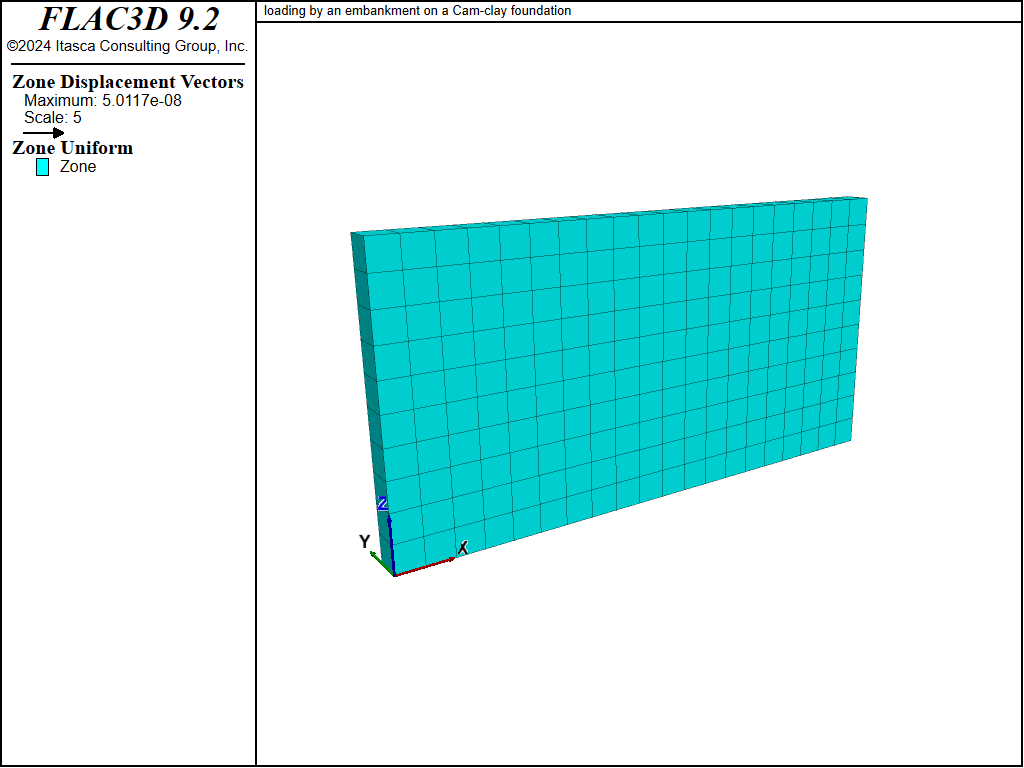
Figure 2: Displacement vectors—undrained response.

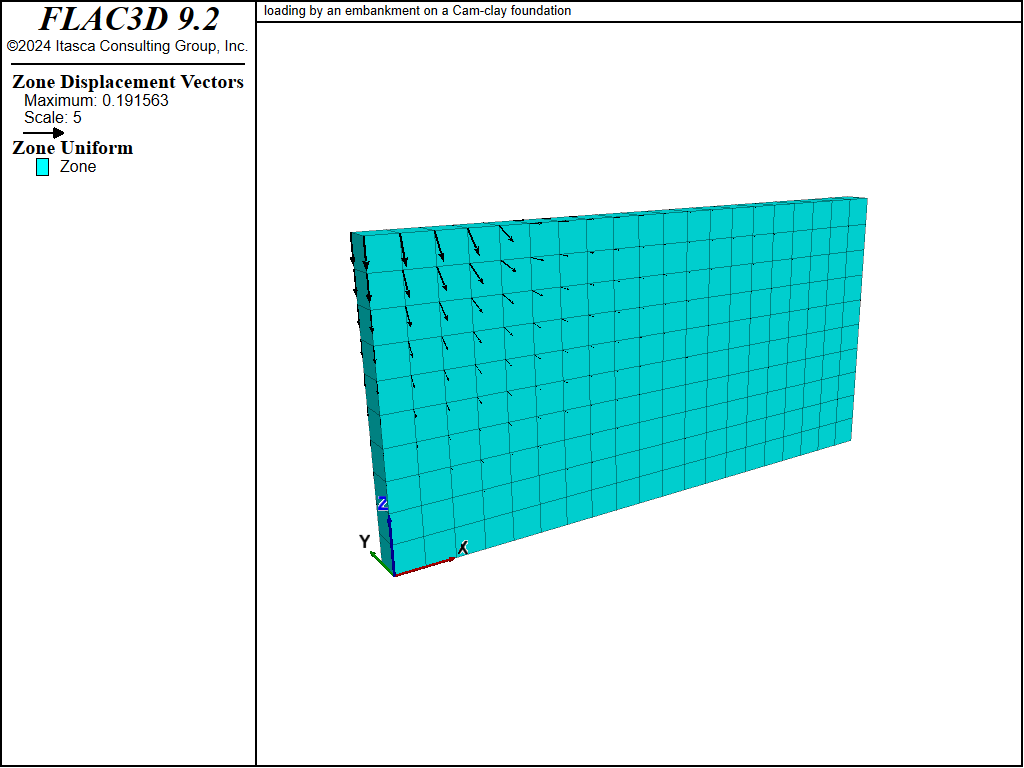
Figure 3: Displacement vectors—end of drained simulation.

Figure 4: Vertical displacement contours—undrained response.

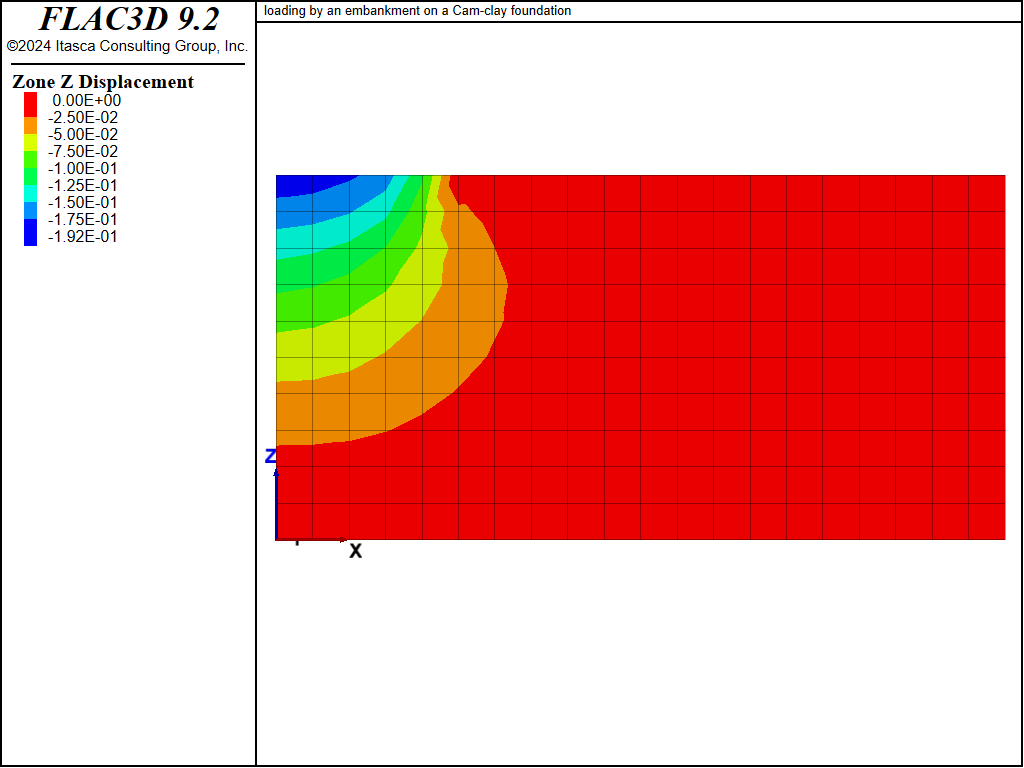
Figure 5: Vertical displacement contours—end of drained simulation.

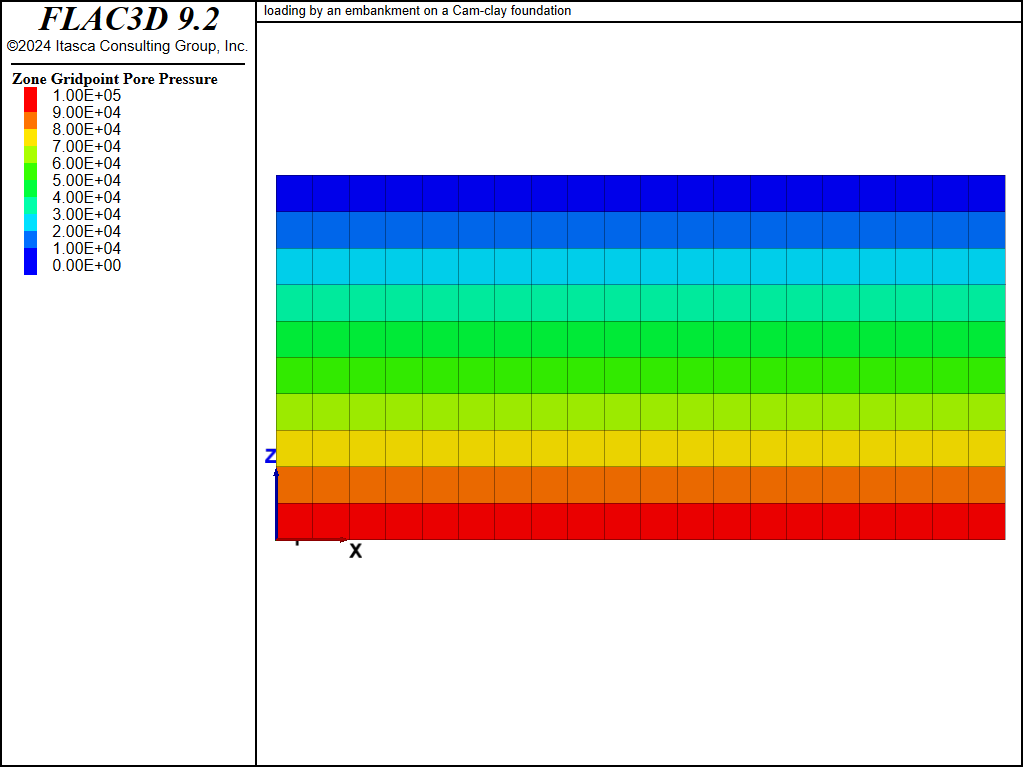
Figure 6: Pore pressure contours—undrained response.

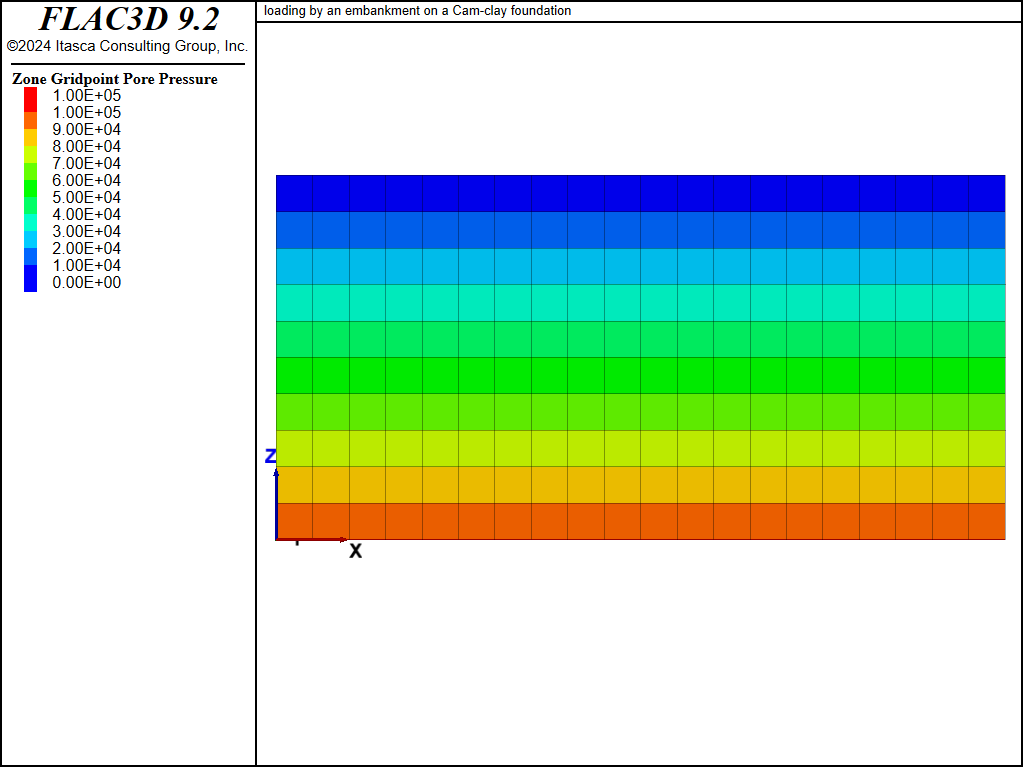
Figure 7: Pore pressure contours—drained response.

Figure 8: Vertical displacement histories—drained response.

Figure 9: Pore pressure histories—drained response.

Data File

EmbankmentLoad.dat

;-----------------------------------------------------------
; Loading by an embankment on a Cam-clay foundation
;-----------------------------------------------------------
model new
model title "loading by an embankment on a Cam-clay foundation"
; -- Create zone geometry
zone create brick point 0 (0,0,0) point 1 (20,0,0) point 2 (0,1,0) ...
                  point 3 (0,0,10) ...
                  size 20 1 10
zone face skin ; Name model boundaries                  
; --- mechanical model and properties ---
model large-strain off
zone cmodel assign modified-cam-clay
zone property poisson .3 bulk-maximum 5e6 density 2000
zone property ratio-critical-state 0.888 lambda 0.161 kappa 0.062
zone property pressure-preconsolidation 160e3 pressure-reference 1e3 
zone property specific-volume-reference 2.858
; -- fluid model and properties
model configure fluid-flow
zone fluid property mobility-coefficient 1e-12 porosity .3
zone fluid property fluid-modulus 2e8 fluid-density 1e3
zone fluid property effective-cutoff -1e20
zone fluid property pore-pressure-generation on
zone fluid conserve-generated on
; --- initial conditions ---
model gravity 10
zone initialize-stresses ratio 0.7
zone gridpoint initialize pore-pressure [1e3*10*10] gradient (0,0,[-1e3*10])
program call 'pressure-effective' suppress ;FISH to initialize CamClay
                                   ;property of mean effective stress
; --- boundary conditions ---
zone face apply velocity-normal 0 range group 'East' or 'West' ...
    or 'North' or 'South'
zone face apply velocity (0,0,0) range group 'Bottom'
zone face apply pore-pressure 0 range group 'Top'
zone face apply stress-normal=-5e4 servo ramp ratio local ...
          range position-x 0 4 group 'Top'
; --- histories ---
history interval 100
zone history name 'z0' displacement-z position (0,0,10)
zone history name 'z2' displacement-z position (2,0,10)
zone history name 'z4' displacement-z position (4,0,10)
zone history name 'z6' displacement-z position (6,0,10)
zone history name 'pp1' pore-pressure position (0.5,0.5,9.5)
zone history name 'pp2' pore-pressure position (1.5,0.5,7.5)
; --- undrained response ---
model solve-static
model save 'undrained'
; --- drained response ---
model history name 'time' fluid time-total
zone fluid implicit servo on error=2e-4
model solve-fluid-coupled time 1e8 convergence 5
model save 'drained'

Endnote

[1]

This example is listed under the present document title in the i Examples dialog (use the menu command Help -> Examples… to access.